负泊松比柔性蜂窝结构在变体机翼中的应用

颜芳芳 徐晓东

南京航空航天大学，南京，210016

0 引言

变体机翼可以根据飞行状态和环境的变化自适应地改变机翼形状，从而显著提高飞行器的综合性能，拓展其使用范围，是未来先进飞行器的一个重要发展方向［1－3］。在机翼连续变体的过程中，要求机翼蒙皮具有良好的面内变形能力和较高的面外刚度，以承受一定的气动载荷。显然，传统的硬壳式蒙皮结构无法同时满足以上要求，故此，基于智能材料的柔性蒙皮结构获得了广泛的研究。

文献［4－8］研究了圆弧型、正弦型等不同形状的波纹蒙皮结构，发现这些结构存在附加重量大和翼面蒙皮不光顺等不足。文献［9］研究了一种碳纤维可变三角形胞状结构，有限元分析表明，这种胞状结构可以满足变体机翼翼型的变化要求。文献［10］研究了蜂窝结构参数对应变的影响。

本文提出了一种具有拉涨特性的负泊松比蜂窝结构，在Gibson和Ashby的蜂窝结构力学基础上，建立了负泊松比蜂窝结构理论分析数学模型，研究了柔性蜂窝结构参数对面内变形能力和面外承载能力的影响。有限元仿真分析与实验验证结果表明，具有拉涨特性的负泊松比蜂窝结构在面内可以产生更大的变形，在垂直方向具有更强的承载能力，具有变体驱动能量低、承载能力均匀和制造工艺简单的特点，适用于变体机翼的结构工程设计。

1 柔性蜂窝蒙皮结构力学特性建模与分析

变体飞行器柔性蒙皮由三层复合材料结构组成，上下面板采用硅橡胶材料，中间芯层为柔性蜂窝结构。假定面板的弹性模量远远低于蜂窝芯层的弹性模量，这时可认为柔性蜂窝结构的变形能力和承载能力只与蜂窝的形状和组合方式有关。柔性蜂窝蒙皮结构如图1所示，蒙皮结构面内方向受到拉伸与压缩作用，该方向刚度较低，可以产生较大变形；而在蜂窝面外方向，具有一定的承载能力，以承受飞行中的气动载荷。

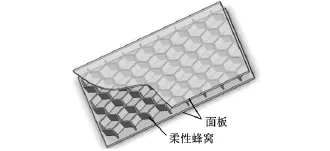
图1 柔性蜂窝夹层结构

1.1 负泊松比弹性蜂窝结构力学模型

比照文献［11－14］列举的几种负泊松比结构，并以类蜂窝形结构为例进行分析研究。图2所示为不同形状细胞单元构成的负泊松比结构。

图3所示为所取的负泊松比弹性蜂窝胞元结构的力学分析情况，规定蜂窝边长为l，蜂窝竖直边高度h＝αl，蜂窝壁板厚度t＝βl，蜂窝壁板倾斜边与竖直边的夹角为θ，取与水平X轴夹角顺时针方向为正，反之为负，图3中的θ为负值。为了避免蜂窝壁板变形后相互层叠，应满足α≥2sinθ。

1.2 负泊松比蜂窝结构面内变形

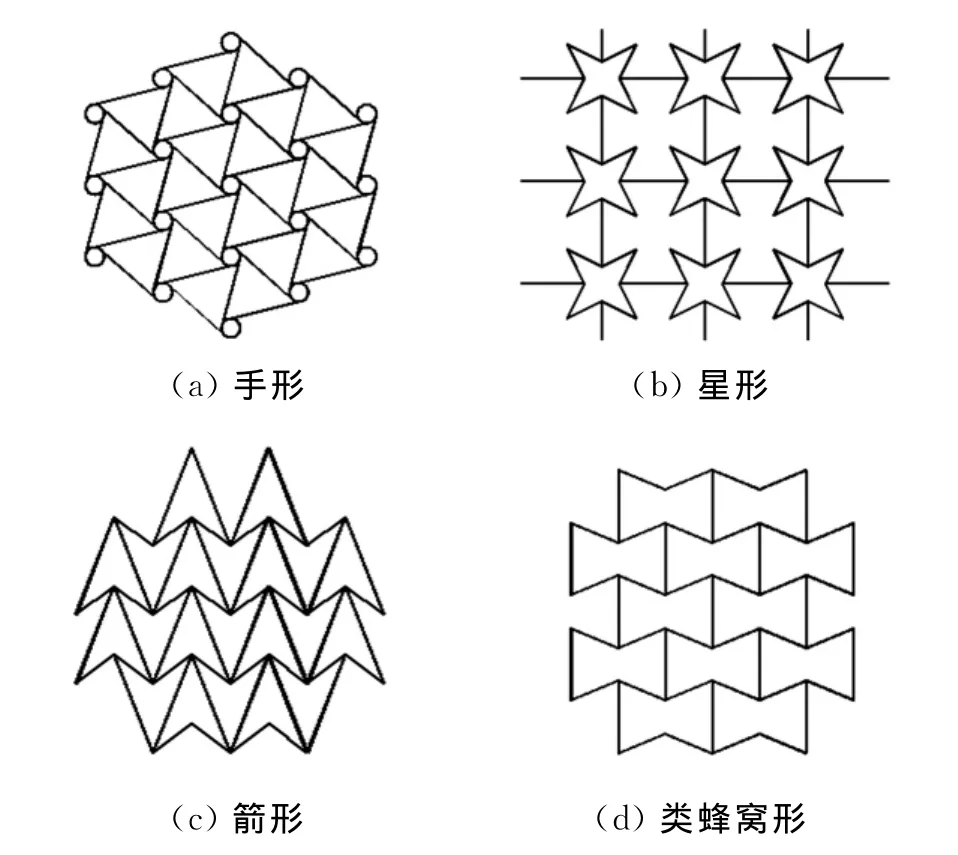
图2 4种负泊松比蜂窝胞元结构

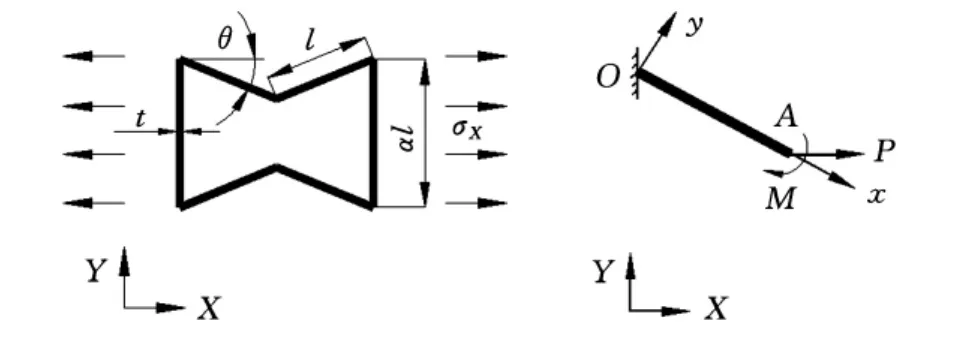
图3 负泊松比蜂窝胞元的力学分析

在线弹性范围内，可以将蜂窝薄壁结构假设为欧拉－伯努利梁（图3），平面应力方向为X方向。取倾斜边蜂窝胞壁为研究对象，以O为原点，沿梁的长度方向设为x轴，垂直于梁的长度方向设为y轴，弹性梁的x轴长度方向形变为δ1，弹性梁y轴方向的形变为δ2。蜂窝壁板梁的末端在水平方向作用集中力P，梁末端的水平位移为δh，垂直位移为δv，根据卡氏定理，梁的总体变形能为

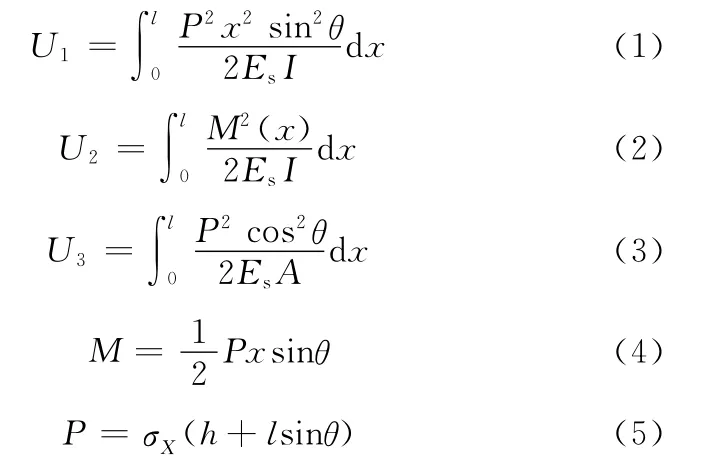
根据卡氏定理，X方向的变形能为UX，Y方向的变形能为UY，其中

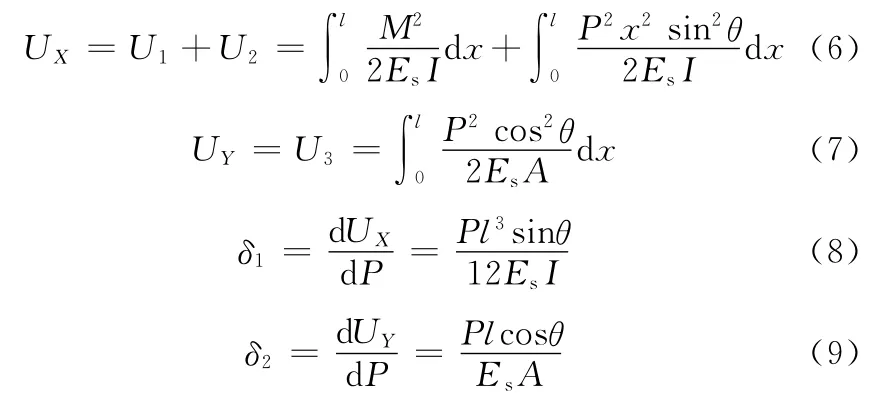
蜂窝结构X方向和Y方向的应变εh、εv可分别表示为

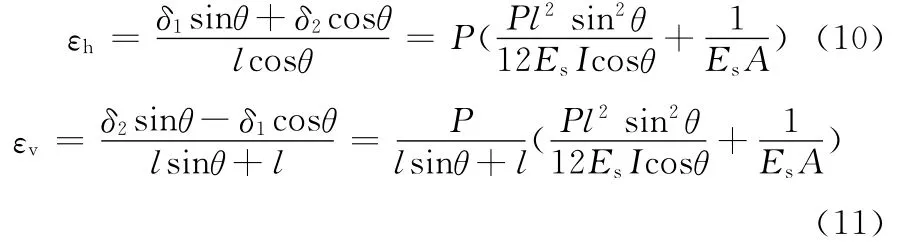
负泊松比柔性蜂窝X方向和Y方向的弹性模量Eh、Ev，以及受X方向平面应力时的泊松比ν1可分别表示为

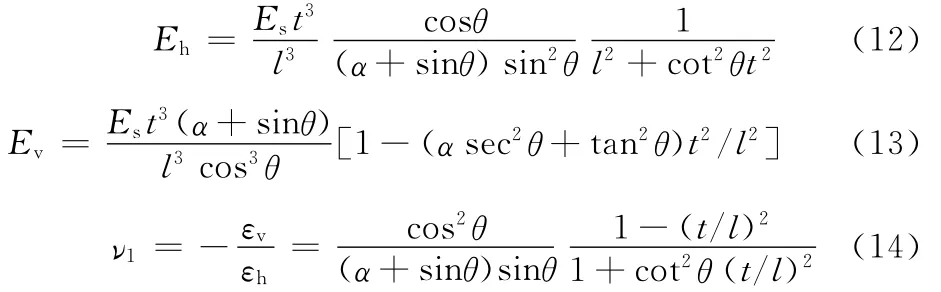
同理，可得泊松比柔性蜂窝结构受Y方向平面应力时的泊松比ν2：

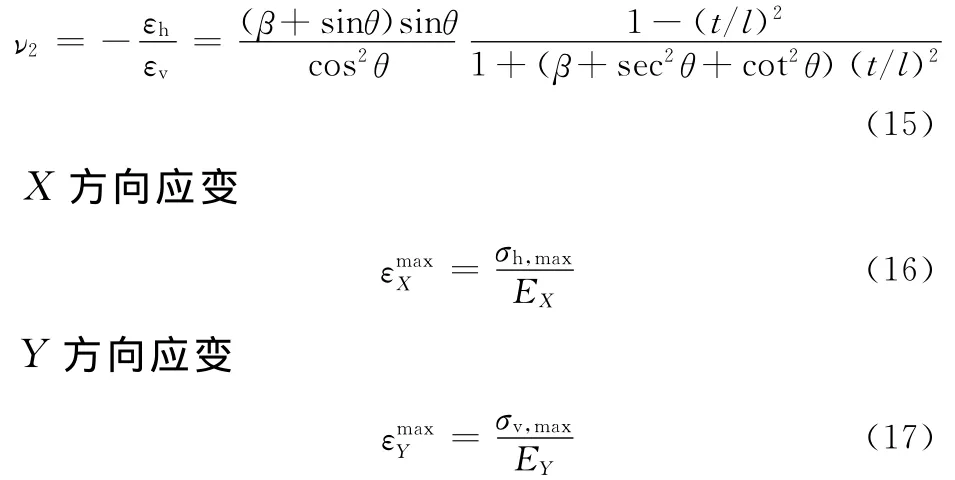
σh，max为负泊松比蜂窝结构线弹性的最大应力，可表达为蜂窝壁板拉伸应力与弯曲应力之和，其中

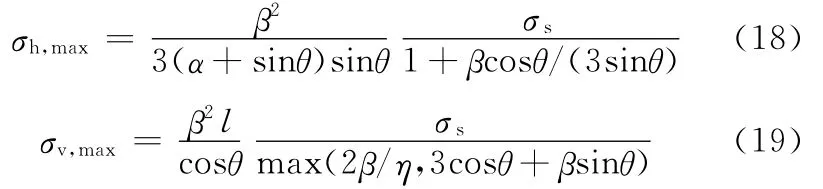
式中，σs为材料的屈服应力。

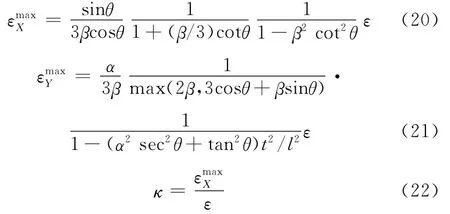
式中，κ为变形比。

显然，变形比κ为蜂窝结构参数的函数，用来衡量柔性蜂窝与各项同性材料的变形能力。

2 柔性蜂窝结构参数对面内变形能力的影响

蜂窝胞元结构的参数对蜂窝结构的变形性能影响较大。当载荷垂直于薄壁结构的平面方向时，薄壁结构的弯曲变形大于薄壁结构的面内变形，蜂窝结构的主要变形为薄壁结构的弯曲变形。对于不同形状的蜂窝单元，蜂窝胞壁长度l、夹角θ以及胞壁厚度t，对蜂窝结构的面内变形影响较为显著。为了弄清柔性蜂窝结构参数对变形的影响，本文重点讨论柔性蜂窝结构参数变化对面内变形能力的影响。取柔性蜂窝胞元l＝10mm，α＝2，H＝20mm，柔性蜂窝结构倾斜边角度θ从－60°变化到60°，增量为5°，变量β分别取为0.05、0.08、0.1和0.2。

图4所示为不同胞壁厚度蜂窝结构随θ变化时，对蜂窝结构面内纵向弹性模量EX的影响，图5所示为不同胞壁厚度蜂窝结构随θ变化时，对蜂窝结构面内横向弹性模量EY的影响，图6所示为不同胞壁厚度蜂窝胞元随θ变化时，对蜂窝结构泊松比ν1的影响。

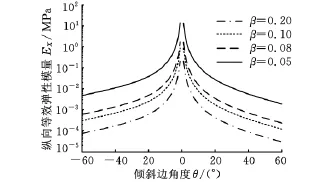
图4 蜂窝胞元厚度t对纵向等效弹性模量EX的影响

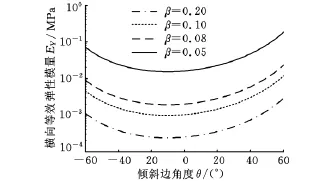
图5 蜂窝胞元厚度t对横向等效弹性模量EY的影响

由图4、图5可知，柔性蜂窝结构在θ＝0°时，纵向弹性模量最大，随着θ的增大或减小，纵向弹性模量降低，横向弹性模量略有增大；随着胞壁厚度的增加和θ的增大，纵、横向弹性模量也相应增大。适当减小胞壁厚度和蜂窝角度可以获得更大的纵向形变。图6所示表明，泊松比随着θ的增大，先增大后减小，当θ为负值时，泊松比也为负值，胞壁厚度越小，泊松比越大。

图7所示为不同胞壁厚度蜂窝结构随θ变化时，对蜂窝结构面内纵向变形比κ的影响。

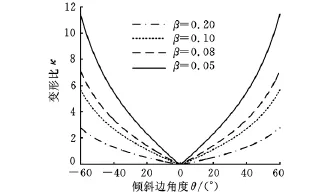
图7 蜂窝胞元厚度t对变形比κ的影响

图4～图7结果表明，柔性蜂窝结构随着参数θ的变化而呈现出不同的力学特性，当θ＝0°时，X方向的弹性模量最大，随着θ的增大，X方向的等效弹性模量进一步降低，变形进一步增大，当β＝0.05时变形比最大，可达原材料的10倍以上，而当θ＝－5°时，泊松比可达原正交同性材料的5倍，故此证明负泊松比蜂窝在面内具有较大的变形能力，且呈现出“拉涨”的特性，利用负泊松比蜂窝的特性，设计弦长与展长同时增大的特殊变体机翼结构，无疑对飞机的起飞和着陆具有重要意义。

3 柔性蜂窝结构参数对面外弯曲刚度的影响

变体机翼的柔性蜂窝结构蒙皮需要呈现各向异性的力学特性，在面内变形方向具有较低的弹性模量，而在面外可以承受一定的气动载荷。柔性蜂窝结构的弯曲刚度可以用等效刚度EI＊来衡量，拉伸模量可以用EA＊来衡量。

采用有限元软件ANSYS和SHELL93单元建立蜂窝试件的有限元模型。柔性蜂窝结构尺寸为220mm×110mm×20mm，蜂窝倾斜边角度为15°时，记为蜂窝Ⅰ，倾斜边角度为0°时，记为蜂窝Ⅱ，倾斜边角度为－15°时，记为蜂窝Ⅲ。蜂窝胞元胞壁长度l＝10mm，α＝1，β＝0.05，H＝20mm。柔性蜂窝结构材料为ABS增强塑料，材料的弹性模量Es＝2016MPa，泊松比νs＝0.41，采用SDPro3000快速成型机制备试件。图8所示为柔性蜂窝Ⅲ有限元模型。

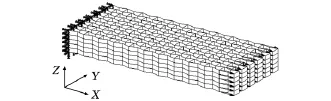
图8 柔性蜂窝Ⅲ有限元模型

进行抗弯刚度研究时，将模型沿长度方向两端固支，在对称中心位置沿宽度方向施加集中载荷P。当载荷较小时，模型沿宽度方向的挠度近似相同。结构的等效弯曲刚度为

式中，ωmax为中性面最大挠度。

表1所示为3种柔性蜂窝结构的有限元仿真结果。

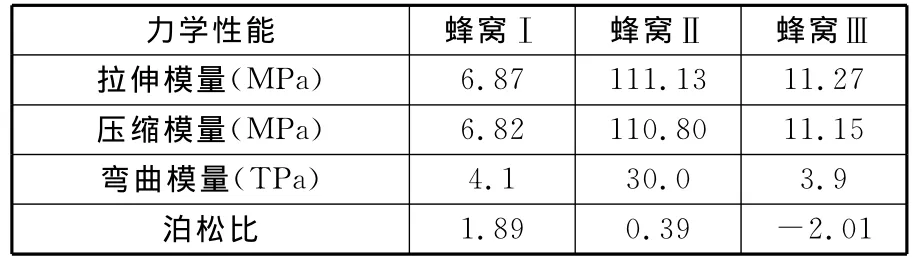
表1 柔性蜂窝结构力学性能仿真

为了衡量柔性蜂窝结构与均匀各项同性材料弯曲刚度性能，取5mm各向同性材料与同质量的柔性蜂窝，建立有限元模型计算等效弯曲刚度比η。图9所示为不同胞壁厚度蜂窝结构随θ变化时，对等效弯曲刚度比η的影响。结果表明，随着β的增大，等效弯曲刚度增强，随着θ的减小，弯曲刚度也降低，说明负泊松比柔性蜂窝结构具有充分的变形能力，但不同角度和厚度的蜂窝结构的面内变形和弯曲变形存在差异。

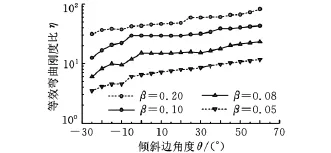
图9 蜂窝胞元厚度t对弯曲刚度η的影响

4 柔性蜂窝力学特性试验验证

对3种柔性蜂窝试件进行面内拉伸和压缩试验，测量当量面内拉伸和压缩模量，并将试验结果与仿真结果进行比较。

面内拉伸和压缩试验在SANS电子万能试验机上进行，利用专用夹具夹持试件两端，沿试件长度方向均匀施加载荷，由位移传感器测量位移，计算面内纵向拉伸和压缩模量。

对柔性蜂窝试件进行抗弯性能试验，对平板试件进行3点弯曲测试（图10），试验过程满足GB／T1456－2005的要求。3种柔性蜂窝结构的等效抗弯刚度及有限元结果比较如表2所示。

图10 3点弯曲试验

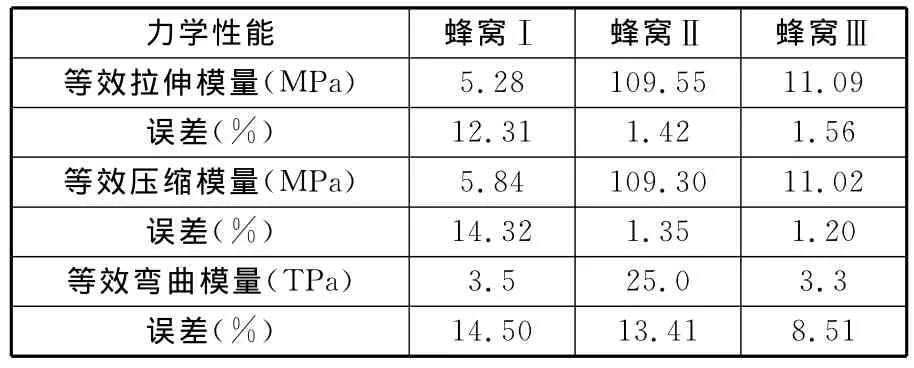
表2 仿真和试验结果

由表2可知，在线性范围内，试验值与仿真结果的最大误差小于15%。负泊松比柔性蜂窝与四边形蜂窝相比，纵向拉伸模量较小，且抗弯刚度略低于常规蜂窝结构，可以获得较大的面内变形，通过优化设计负泊松比蜂窝结构参数，可以满足特殊结构的变形与刚度要求。

5 结论

（1）本文针对可变弯度机翼，设计了一种柔性蜂窝结构。该柔性蜂窝结构面内方向具有充足的面内变形能力，面外方向可以具备一定的承载能力，能够满足变体机翼柔性蒙皮结构各向异性的力学性能要求。

（2）本文将柔性蜂窝结构应用于无人机外翼结构，在实现后缘结构偏转的同时，增大了翼展方向机翼的面积，对无人机起飞和着陆性能的提高具有重要价值。

（3）本文尚未考虑柔性蜂窝机翼结构的应力分布和气动弹性等问题，对柔性蜂窝应用于变体机翼结构的驱动方式、驱动特性，以及动态响应等问题还未做深入研究，需要在后续工作中展开。

［1］Gandhi F.Skin Design Studies for Variable Camber Morphing Airfoils［J］.Smart Materials and Structures，2008，17（1）：015025－015033.

［2］Kudva J.Overview of the DAPRA Smart Wing Project［J］.J.Intell.Mater.Syst.Struct.，2004，15（26）：1－7.

［3］Monner H P.Realization of an Optimized Wing Camber by Using Form Variable Flap Structures［J］.Aerospace Science Technology，2001，5（7）：445－455.

［4］Yokozeki T，Takeda S I，Ogasawara T，et al.Mechanical Properties of Corrugated Composites for Candidate Materials of Flexible Wing Structures［J］.Composites，2006，37（10）：1578－1586.

［5］牟常伟，王帮峰，葛瑞均，等.纤维增强复合材料波纹蒙皮机体的承载能力［J］.材料科学与工程学报，2010，28（4）：597－602.

［6］戚健龙，徐志伟，朱倩，等.变体机翼大变形梯形蒙皮结构研究［J］.功能材料，2011，42（1）：108－111.

［7］Thill C，Etches J A.Composite Corrugated Structures for Morphing Wing Skin Applications［J］.Smart Materials and Structures，2010，19（12）：124009－124019.

［8］张平，周丽，邱涛.一种新的柔性蜂窝结构及其在变体飞机中的应用［J］.航空学报，2011，32（1）：156－163.

［9］Bettini P，Airoldi A，Sala G，et al.Composite Chiral Structures for Morphing Air Foils：Numerical Analyses and Development of a Manufacturing Process［J］.Composites，2010，41：133－147.

［10］Olympio K R，Gandhi F.Flexible Skins for Morphing Aircraft Using Cellular Honeycomb Cores［J］.Journal of Intelligent Material Systems and Structures，2010，21（9）：1719－1735.

［11］Prall D，Lakes R.Properties of a Chiral Honeycomb with a Poisson’s Ratio－1［J］.International Journal of Mechanical Sciences，1996，39：305－314.

［12］Theocaris P S，Stavroulakis G E，Panagiotopouls P D.Negative Poisson’s Ratios in Composites with Starshaped Inclusions：a Numerical Homogenization Approach［J］.Archive of Applied Mechanics，1997，67（4）：274－286.

［13］Larsen U D，Sigmund O，Bouwstra S.Design and Fabrication of Compliant Micromechanisms and Structures with Negative Poisson’s Ratio［J］.Journal of Microelectromechanical Systems，1997，6：99－106.

［14］杨志春，邓庆田.负泊松比材料与结构的力学性能研究及应用［J］.力学进展，2011，41（3）：335－340.