基于机体翻转的四足机器人翻越台阶过程的运动学分析
余联庆 王玉金 王立平 汪红波 唐焱明
1.武汉纺织大学,武汉,430073 2.清华大学,北京,100084
3.浙江师范大学,金华,321019 4.鄂东职业技术学院,黄冈,438000
0 引言
在自然界和人类社会中,存在人类无法到达的地方和可能危及人类生命的特殊场合,如行星表面、工地、矿井、防灾救援的地方等。不规则和不平坦的地形是这些环境的共同特点,这使轮式机器人和履带式机器人的应用受到限制。由于足式机器人可以利用孤立地面作为支撑,具有较强的地形适应性。在这种背景下,足式机器人的研究便蓬勃发展起来[1]。由于四足机器人具有较好的行走适应性和稳定性,所以国内外开发了多种各具特色的四足机器人[2-4]。
在非结构化环境中,平坦的地面十分有限,并且障碍物的形状和大小不可预测。障碍物大体可以分为两大类[5]:一类是体积远大于机器人系统、机器人系统无法逾越的障碍物,如水池、悬崖等,这时机器人必须绕道行驶或者另外规划目标路径;另一类是体积与机器人相当、机器人通过改变自身的构形可以逾越的障碍物,包括坡型、台阶型和沟壑等障碍物。一般说来,机器人通过两种基本方法改变自身构形[6]:一为“重构”,即模块的重组;二为“变形”,即本身关节的运动。国外学者做了大量的研究工作,研制了各种各样的可重构机器人[7-9]。四面体滚动机器人[10]及滚动三角形机器人[11]就是可变形重构的机器人,通过改变伸缩臂长度来实现机器人的变形与移动。但此类机器人的越障速度和能力较低,移动过程不连续,很难在实际中得到运用。
四足机器人传统的越障方式是:采用三条腿作支撑,另一条腿跨越障碍,直至四条腿均越过障碍。四足机器人前后双腿均含有髋关节、膝关节和踝关节,具备改变自身构形的能力。本文充分利用四足机器人的关节运动变形能力,提出一种基于机体翻转的台阶翻越方式。首先对机器人翻转式翻越台阶周期进行了运动规划,然后对翻越过程进行了运动学建模与仿真分析,得到机器人各个关节角的变化曲线以及重心的移动轨迹。最后讨论了机器人台阶翻越能力与几何参数之间的关系。为了方便叙述,在下文中将翻越台阶简称为越障。
1 四足机器人结构模型
机器人的本体结构直接影响到机器人的性能和技术指标,本文采用类似哺乳动物的四足机器人结构模型,如图1所示。四条腿采用同样的结构,每条腿均含有三个主动关节,即髋关节、膝关节和踝关节。大腿与小腿的长度相等,且为机体长度的一半。由于臀关节轴心线和机器人机体平面平行,所以髋关节可以绕轴线旋转360°。假设足底与地面的摩擦因数足够大,在越障过程中不会发生足底打滑现象。
2 翻转式越障运动规划
四足机器人以翻转方式越障时,前后双腿分别执行相同的动作,在运动学分析时可将前后双腿分别合并为一条腿。在越障时不考虑转向问题,因此可将越障运动视为平面运动。从而将四足机器人越障运动分析转化为平面连杆机构的运动分析。
受到背越式跳高的启发,本文对四足机器人翻转式越障进行了运动规划,如图2所示。一个完整的运动周期包括5个阶段:①从站立到前双腿膝关节着地(图2a);②后双腿越障(图2b);③机体姿态的调整(图2c);④前双腿越障(图2d);⑤机器人正常站立(图2e)。每个阶段中机器人的开始姿态用实线表示,结束时的姿态用虚线表示。
机器人从左往右运动,前肢的踝关节、膝关节和髋关节分别用A、B、C表示;D、E、F分别表示后肢的髋关节、膝关节和踝关节。
3 运动学分析模型
四足机器人在翻转式越障周期中,姿态会随着不同的阶段而变化,其运动学模型也要发生相应的变化。在以下的运动学分析中为了方便描述,以L1和L2分别表示前肢小腿和大腿,其长度分别用l1和l2表示;机体用L3表示,其长度用l3表示,O表示质心;后肢大腿和小腿分别用L4和L5表示,其长度分别用l4和l5表示。以θij表示机体或腿Li到Lj的逆时针夹角,当i或j为0时,表示直角坐标系x轴正向。以θ0ij表示一个运动阶段的关节初始角,θ′ij表示该运动阶段末时刻的关节角。
3.1 前双腿膝关节着地阶段
机器人从站立到前双腿膝关节着地的位姿变换过程中,足底始终与地面保持接触,足与地面无相对滑动,可把足底与地面的约束看作固定约束。机器人由站立到前双腿膝关节着地的位姿变换过程如图3所示,虚线所示为位姿变换完成时的姿态,取关节点F为原点,建立直角坐标系Fxy。
大腿与小腿长度相等,且为机体长度的一半,则
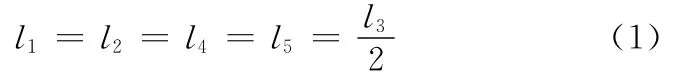
平面连杆机构的自由度计算公式:
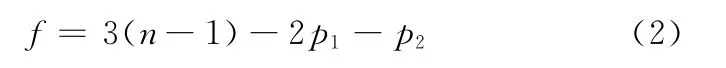
式中,n为平面连杆机构的构件数目;pi为自由度为i的运动副数目。
由式(2)可得图3中所示机构自由度f=3,设定主动输入为关节A、E和F。在图3所示的前双腿膝关节着地阶段,各关节角的初始角度以及膝关节着地结束时的角度如表1所示。

表1 前双腿膝关节着地阶段的关节夹角 (°)
前双腿膝关节着地的时间为0→ta,将输入关节的速度均取匀速,则由表1中各个关节角的初始角以及末时刻夹角可得:
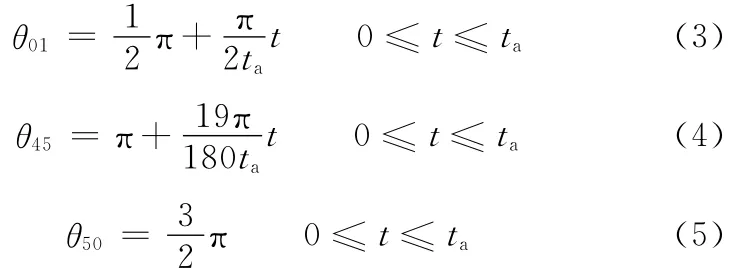
在图3所示的位姿变换运动过程中,其运动回路矢量方程为
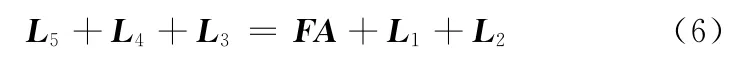
关节F到关节A的距离与l3相等,将式(6)写成在直角坐标系Fxy中的标量形式为
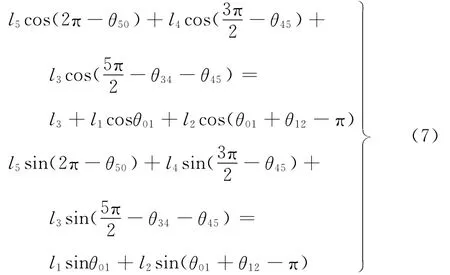
求解式(7)可得
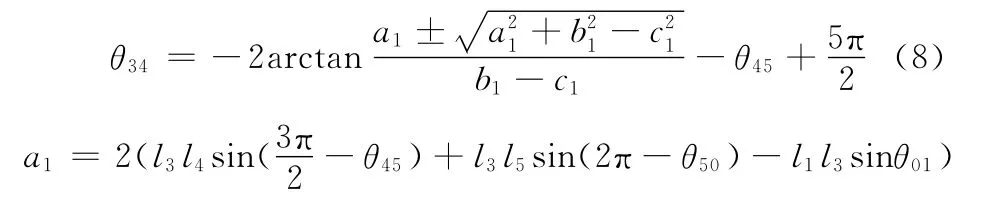
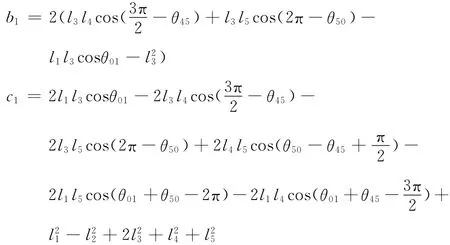
同理,求解式(7)可得:
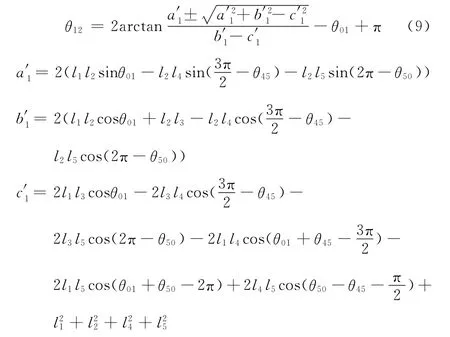
另外,θ23的求解公式如下:
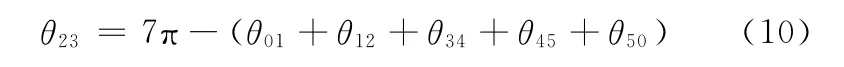
机器人由站立到前双腿膝关节着地质心O的坐标公式如下:
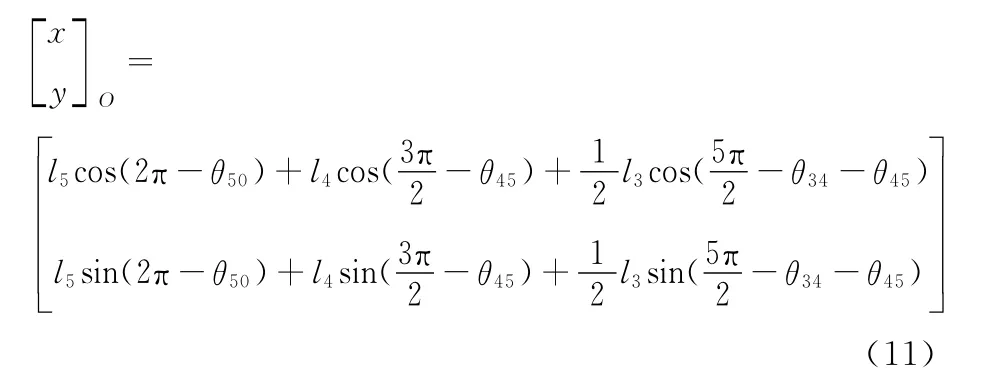
3.2 后双腿越障
在后双腿越障阶段,腿L1与腿L2固定,使其保持在前肢膝关节着地完成时的姿态,则后双腿越障的运动学模型可简化为一单开链平面四杆机构,取关节点B为原点,在其上建立坐标系Bxy,如图4所示。
由图4可以得出,在后双腿越障过程中,各关节的初始角以及末时刻的角度如表2所示。
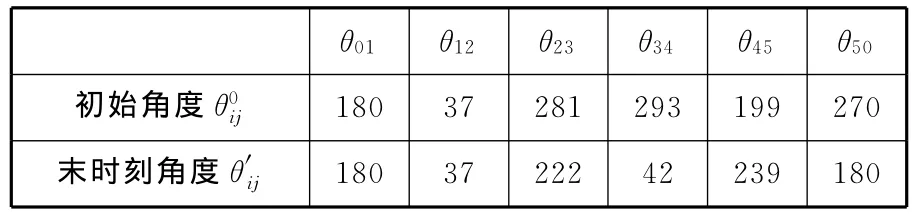
表2 后双腿越障的关节夹角 (°)
由图4所示的运动学模型以及式(2)可以得出腿L5的末端自由度f=3。设定关节C、D、E为输入关节,后双腿越障的时间为ta→tb,且输入均为匀速。为保证机器人的运动空间与障碍不发生干涉,使关节角θ45以及θ34先达到预定的值,再令关节C旋转,则各关节的角度方程如下:

其中,tb1为关节C开始运动的时刻。关节角θ50分为两个阶段,θ50为270°→360°时为一个阶段,θ50为360°→180°(即0→180°)时为一个阶段,则
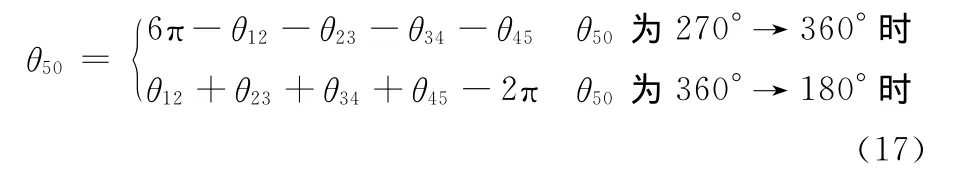
机器人在后双腿越障过程中质心O的坐标为
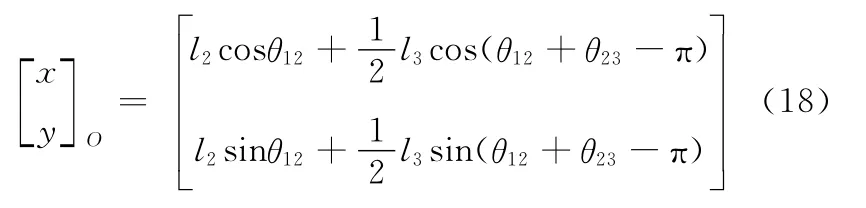
双腿越障完成后,关节点B和E′之间的y轴方向距离即为机器人的越障高度h,其计算如下:
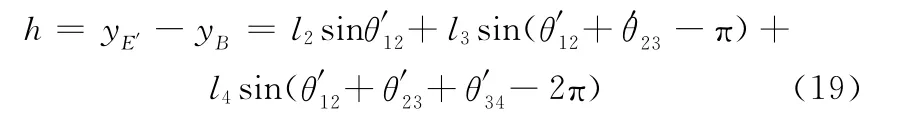
3.3 机体姿态调整
机体姿态调整阶段,腿L5与地面平行接触且无相对运动,腿L1的踝关节A与足仅有相对转动,且足底与地面为固定约束。机器人运动简图可转化为一单闭链平面五杆机构,取关节点A为原点,在其上建立直角坐标系Axy,如图5所示。
由式(2)可知,机体姿态调整阶段自由度f=2,设定关节A、E为主动关节,其余关节为被动关节。机体姿态调整的时间为tb→tc。机体姿态调整的初始关节角及末时刻关节角见表3。

表3 机体姿态调整关节角 (°)
由机体姿态调整运动模型以及主动关节初始角和末时刻夹角,令
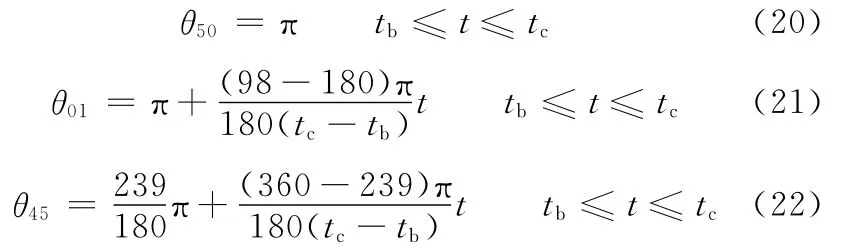
如图5所示,机体姿态调整运动回路矢量方程为
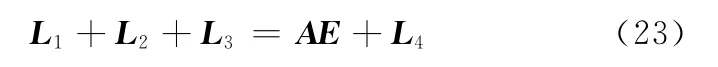
将式(23)改写为在坐标系Axy中的分量形式:
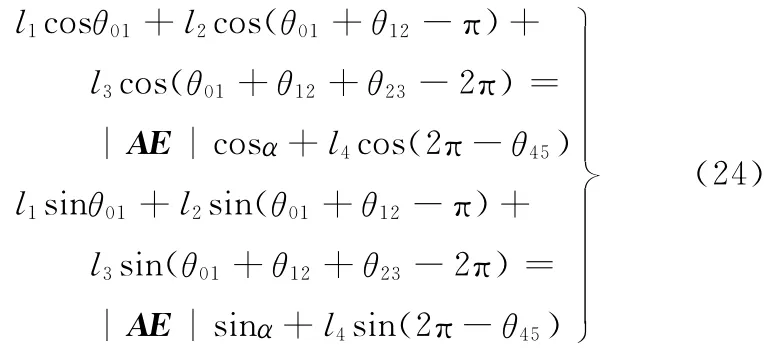
由式(24)可解得
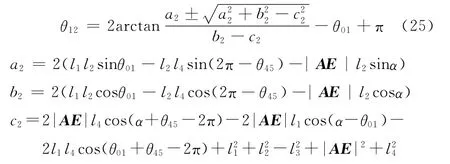
同理,可得
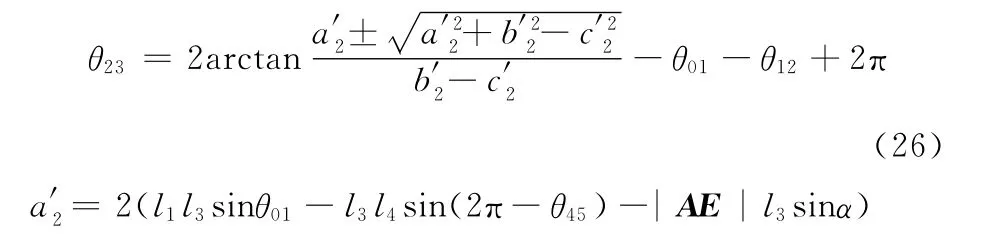
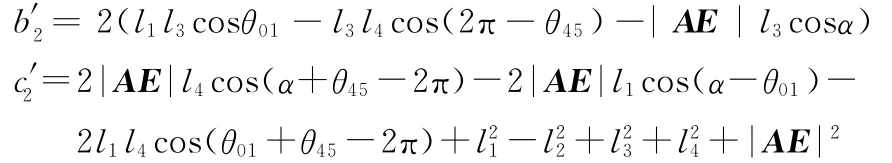
由图5和图4可知,在式(23)~式(26)中,有
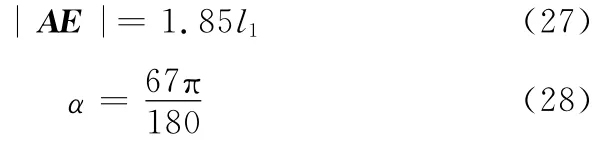
由图5所示的运动关系,可得
θ34=4π-(θ01+θ12+θ23+θ45)(29)
机器人在机体调整阶段质心O的坐标为
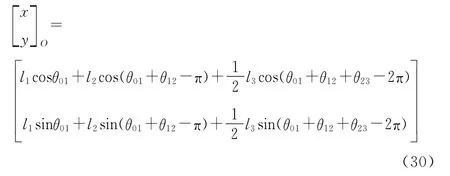
3.4 前双腿越障
前双腿越障阶段,腿L5固定于地面,将腿L5取出,并令腿L1与腿L2之间的夹角θ12保持不变,则腿L4、机体L3以及腿L1与腿L2的组合是开链四杆机构,其自由度f=3,取E关节点为原点,建立坐标系Exy,运动模型如图6所示。
设定关节C、D、E为输入关节,前双腿越障作用时间为tc→td,其初始角以及末时刻的关节角见表4。
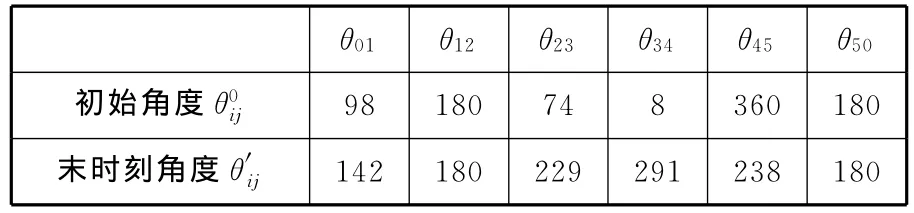
表4 前双腿越障关节角 (°)
由初始角、末时刻角以及输入关节运动关系,令
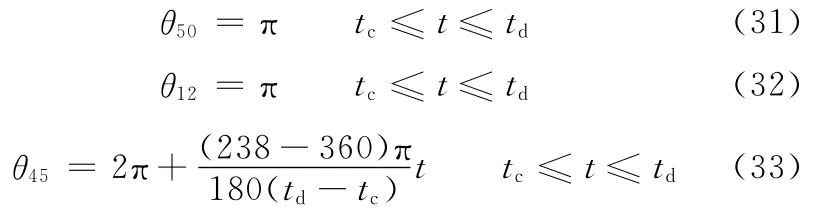
关节D和关节C同样取匀速运动,可以保证工作过程中,质心O始终落在支撑范围内,则
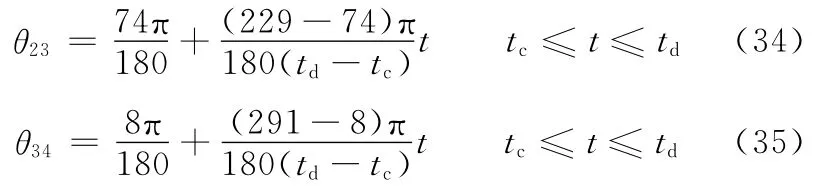
关节角θ01可分为两个阶段,当θ01为98°→0时为一阶段,当θ01为0→142°(即360°→142°)时为一阶段,则
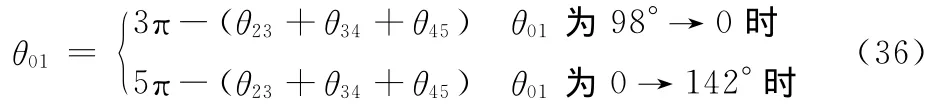
前双腿越障阶段,机器人质心O的坐标为
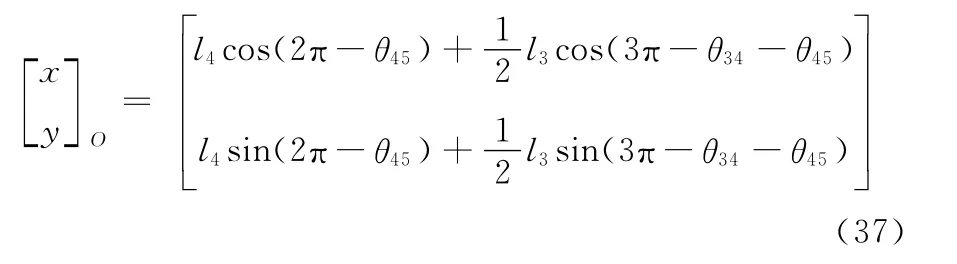
3.5 机器人正常站立
机器人正常站立运动学模型如图7所示,在关节点F建立坐标系Fxy。保持腿L1与腿L2的关节角θ12不变,则图7所示机构的自由度f=2,其运动学模型可看着单闭链平面五杆机构,设立关节A、F作为主动关节。正常站立时间为td→te,初始及末时刻关节角见表5。
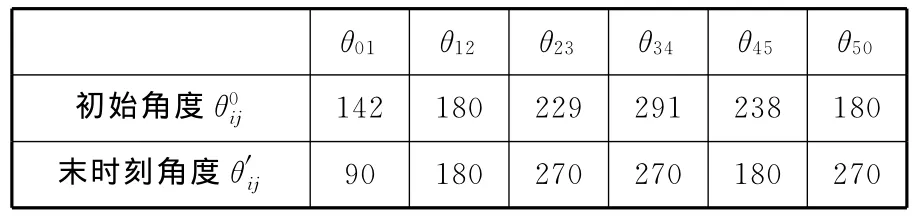
表5 正常站立关节角 (°)
正常站立过程中,腿L1与L2关节角θ12不变,并取关节A和关节F为匀速,则
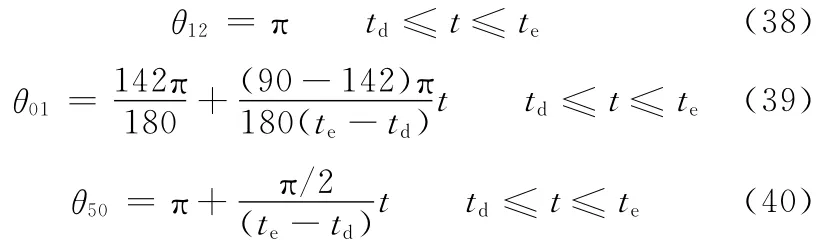
如图7所示,机器人正常站立运动回路矢量方程为
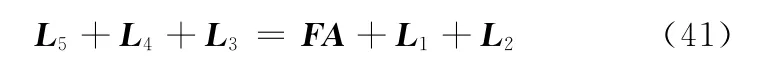
式(41)在坐标系Fxy中的标量形式为
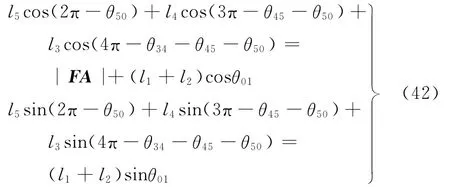
其中,关节F和关节A之间的距离:
|FA|=l3(43)
由式(41)和式(42)可以解出:
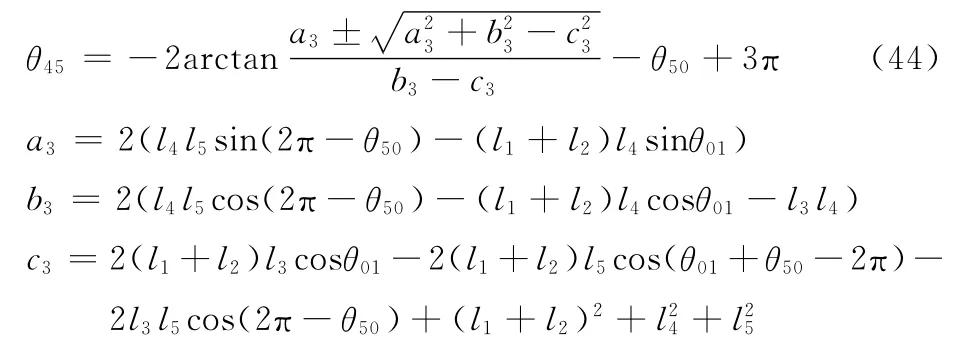
同理,可得
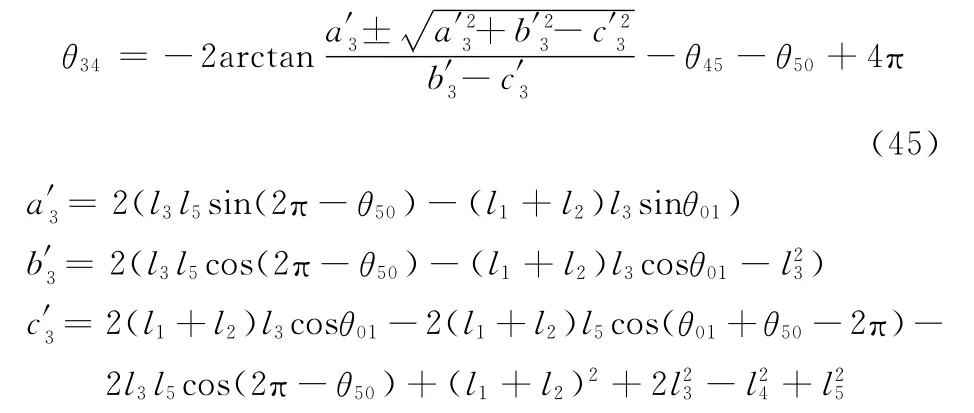
而关节角θ23为
θ23=6π-(θ01+θ34+θ45+θ50)(46)
机器人质心O的坐标公式为
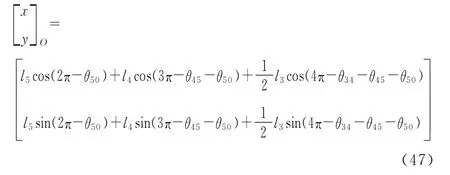
4 仿真分析
各关节角的角度方程建立后,根据式(1)取l1=0.5m对机器人越障运动进行仿真。以翻转式越障周期第一运动阶段所建立的坐标系Fxy为基准,其余运动阶段所设定的坐标系转化到基准坐标系中。根据上文中的运动学分析模型,利用MATLAB编程计算可以得出机器人在翻转式越障阶段各关节角位移的变化曲线,如图8所示,以及质心O的横坐标和纵坐标变化曲线,如图9所示。
5 越障能力分析
越障能力和机器人的几何参数、运动方案以及越障时机器人与障碍物的距离有关,下面讨论在现有的几何参数并在规划的运动方案下机器人的越障能力。
机器人在整个翻转式越障周期中,机体翻转阶段有两个:后双腿越障和前双腿越障阶段。机体在两次翻转过程中需保证机体质心O在支撑面内。在后双腿越障阶段(图4),质心O必须在支撑面内,即

在前双腿越障阶段(图6),机器人质心O必须在支撑面内,即

由图9所示的变化曲线可以看出该运动方案满足翻转条件。综合关节角的运动空间、机械结构参数等可以得出机器人的最大越障高度为

则后双腿翻转越障完成时,机器人的机体L0、腿L3以及腿L4重合。
6 结束语
为了提高四足机器人的越障能力,本文提出一种基于机体翻转的台阶翻越方式,并对其进行了运动规划和运动学仿真分析。分析中将机器人的结构简化为平面连杆机构,使得仿真分析变得简单。在给定输入规律的情况下,得出了翻越台阶过程中各关节的角位移变化曲线以及重心的移动轨迹,从运动学角度验证了该越障方法的有效性和可行性。本文对足式机器人的越障方式进行了有益的探索,为进一步的研究提供了理论基础。
[1]陈学东,孙翊,贾文川.多足步行机器人运动规划与控制[M].武汉:华中科技大学出版社,2006.
[2]黄博,王鹏飞,孙立宁.基于行为模式的复合运动方式四足机器人研究[J].中国机械工程,2007,18(18):2159-2162.
[3]刘静,赵晓光,谭民.腿式机器人的研究综述[J].机器人,2006,28(1):81-88.
[4]Takahashi M,Yoneda K,Hirose S.Rough Terrain Locomotion of a Leg-wheel Hybrid Quadruped Robot[C]//IEEE Int.Conf.on Robotics and Automation.Orlando,USA,2006:1090-1095.
[5]张力平,马书根,李斌,等.可重构模块化机器人系统的翻越台阶能力研究[J].中国机械工程,2009,20(12):1407-1412.
[6]王婧,李斌,马书根,等.模块化可变形机器人控制系统设计与变形方法研究[J].机器人,2006(9):457-462.
[7]Phipps C C,Shores B E,Minor M A.Design and Quasi-static Locomotion Analysis of the Rolling Disk Biped Hybrid Robot[J].IEEE Transactions on Robotics,2008,24(6):1302-1314.
[8]Yim M,Zhang Y,Roufas K.Connecting and Disconnecting for Chain Self-reconfiguration with Polybot[J].IEEE/ASME Transactions on Mechatronics,2002,7(4):442-451.
[9]Murphy R,Casper J,Hyams J.Mobility and Sensing Demands in USAR[C]//IEEE Industrial Electronics Conference.Piscatoway,USA,2000:138-142.
[10]毕树生,张利格.具有并联机构的四面体翻滚机器人:中国,200910093258.X[P].2010-03-10
[11]孔德隆,刘伟,徐文胜,等.一种滚动三角形机器人:中国,200910076337.X[P].2009-10-21.

