舰船辐射噪声总声级及总能量的统计分析
田 池,刘雨东,张 宇
(1.水下测控技术重点实验室,辽宁 大连116013;2.大连测控技术研究所,辽宁 大连116013)
0 引 言
舰船辐射噪声是由舰船上机械运转和舰船运动产生并辐射到水中的噪声,它是由离开舰船一定距离的水听器接收到的舰船噪声。舰船辐射噪声和一般的信号不同,一般的信号可以用1 个预先确定的时间函数来描述,而噪声只能通过长时间的观测来得到它的随机变化规律。所以,噪声是一个随机过程。在统计学中,通常用1 个随机函数来描述这种随机过程。既然噪声是一种随机过程,相应地,在某一时刻,噪声声压值或置于噪声场中的水听器输出端的噪声电压相应地也是随机变量[1]。舰船噪声可以用声压p、质点振速v 和声强I 等基本量来描述,但为了计算方便往往将这些基本量取对数,用dB 来表示,也称为级表示,如声压级、声强级和质点振速级等[2]。总声级即为总能量取对数后的结果。
1 舰船辐射噪声总声级及总能量
总声级又称宽带声压级,它是在指定频率范围内,将声压与基准值比值的平方取对数得到,其计算公式为
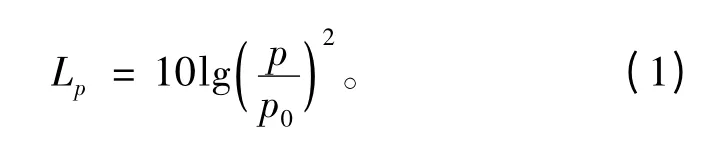
式中:Lp为总声级;p 为声压值;p0为声压基准值。
对于某一特定舰船来说,在相同工况下,对该舰船辐射噪声测量得到的总声级应该是1 个常数。然而在实际中,因为海区环境的复杂性以及舰船上大量机械设备的运转,如不圆的轴或电机电枢的旋转、往复式内燃机气缸中的爆炸等造成的设备耦合导致测得的舰船辐射噪声信号的总声级和总能量是1 个随机变量。
这里,样本数据来源于海试中对某舰船辐射噪声多次的测量。在测量过程中,该舰船基本处于相同工况,共得到65 个样本数据,根据样本数据,得到总声级和总能量的直方图分布如图1 和图2所示。
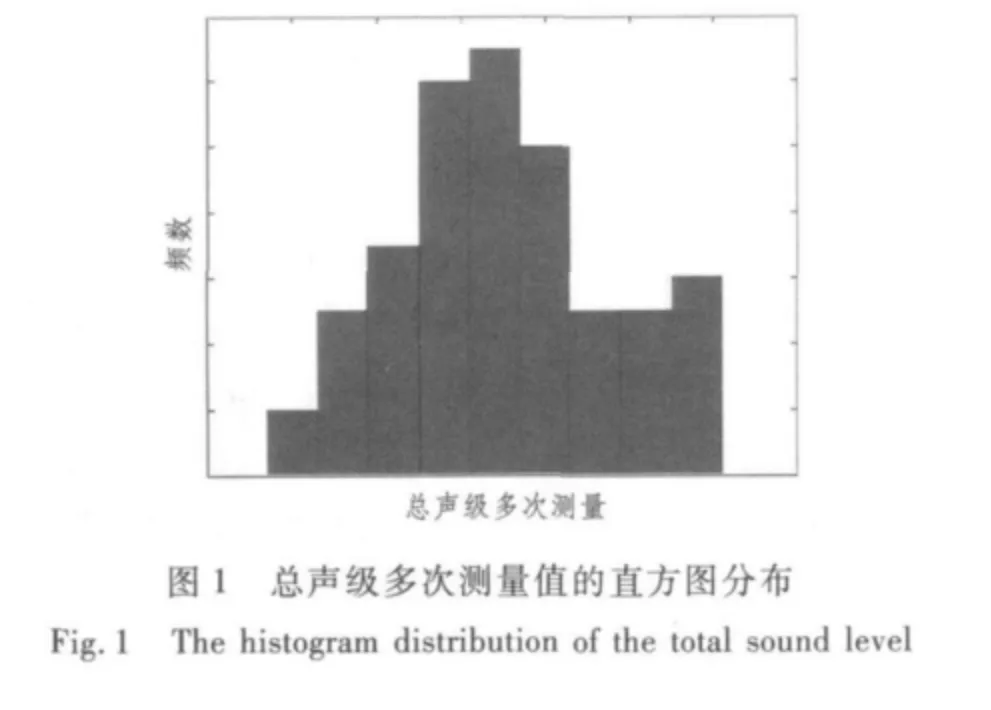
由于试验条件有限,未能得到在相同工况下,该舰船辐射噪声的大量样本。但从图中大致可以看出一些规律:总声级的多次测量结果主要集中在中间部分,越往两边频数越小,并且计算得到的总声级多次测量值的样本偏度为0.146 5;而总能量的多次测量结果很明显不是关于中间部分对称,其频数最大值靠近前半部分,并且计算得到的总能量多次测量值的样本偏度为0.466 9。我们知道,对于一个正态分布随机变量,其偏度为0。因此,假设总声级满足正态分布,而总能量不满足正态分布。下面对总声级进行验证分析。
2 总声级的假设检验
在假设检验问题中,如果总体的分布类型已知,其中仅含有有限个未知参数,而我们要做的只是对这些参数进行检验,称为参数检验问题。如果总体分布类型未知,或者知之甚少,这时所做的就是非参数假设检验。这里,样本数据适用于非参数假设检验。下面介绍2 种常用的非参数假设检验,即皮尔逊χ2拟合检验和柯尔莫哥洛夫检验,分别用它们对总声级进行验证分析。
2.1 皮尔逊χ2拟合检验
拟合检验又叫拟合优度检验。它的一般提法是:设有一个可观察的一维或多维的随机变量X,X1,X2,…,Xn是X 的独立观察值,F0(x)是一个完全已知或类型已知但依赖于若干个未知参数的分布函数,其维数与X 的维数相同,要利用样本X1,X2,…,Xn去检验假设
H0:X 的分布函数为F0(x)。
或者也可以这样提:如果用分布函数F0(x)去拟合样本X1,X2,…,Xn,则拟合的优良程度如何。F0常称为理论分布[3]。
在这里,理论分布我们认为是正态分布,但其中包含若干个未知参数,这时检验问题为
拟合检验的一般步骤如下:
1)在H0成立之下,求出未知参数μ,σ 的极大似然估计;
2)适当选择常数a1,…,ak-1,满足-∞ <a1<a2<… <ak-1<∞把(-∞,+∞)分成k 个互不相交的区间:I1=(-∞,a1),I2=[a1,a2),…,Ik=[ak-1,∞),记

3)算出Ii中样本值的个数ni,并计算Pearson 统计量的值

4)查χ2分布表,找出或m-1),这里α 为显著性水平,m 为未知参数个数;
按照拟合检验的一般步骤,代入总声级多次测量数据,这里k 取值为4,m 取值为2,计算得到χ2=1.402,并根据χ2分布表,最终形成皮尔逊χ2拟合检验分布结果如表1所示。

表1 皮尔逊χ2拟合检验分布表Tab.1 The distribution forms of Pearson χ2fit test
P{当H0为真时拒绝H0}≤α。
当样本容量固定时,若减小犯一类错误的概率,则犯另一类错误的概率往往增大,若要使犯2 类错误的概率都减小,除非增加样本容量,在给定样本容量的情况下,一般来说,我们总是控制犯第Ⅰ类错误的概率,使它不大于α,通常工程上α 取小于0.1 的值[4]。本文中,拒绝原假设成立的最大概率为0.236,满足工程上的应用,因此我们接受H0假设,认为总声级多次测量值服从正态分布。
2.2 柯尔莫哥洛夫检验
首先考虑假设
H0:F(x)=F0(x),
其中,F0(x)是完全已知的连续型分布函数,这里我们认为是正态分布。
我们知道,当样本容量n 充分大时,经验分布函数Fn(x)与总体分布函数F(x)相当接近。所以,当H0成立且n 较大时,Fn(x)与F0(x)的差距不应太大。由于Fn(x)和F0(x)都是x 的单调非降函数,所以偏差的上确界可在n 个点X(i)处找,因而柯尔莫哥洛夫检验是先在样本的每个顺序统计量X(i)上求样本经验函数和假设的分布函数之间的偏差中较大的一个,即求
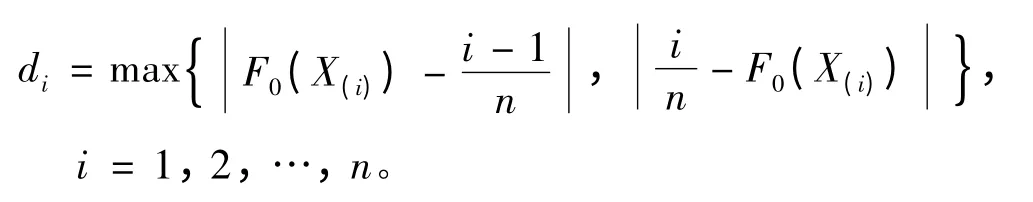
而这n 个di中最大的一个就是柯尔莫哥洛夫检验统计量Dn的取值,即
Dn=max{d1,d2,…,dn}。
若Fn(x)与F0(x)拟合得好,则Dn的值应比较小;反之,当Dn较大时,Fn(x)与F0(x)拟合得不好。
当总体分布含有未知参数时,先估计出未知参数,然后根据Dn值的计算方法计算出对给定的显著性水平α,检验规则为:若则拒绝H0,否则就接受H0。对于α=0.01,0.05,0.10,0.15,0.20,Lilliefors 给出了的临界值[5]。
根据柯尔莫哥洛夫检验方法,代入总声级的多次测量数据,计算得到,并根据的临界值表,最终形成柯尔莫哥洛夫检验分布结果如表2所示。

表2 柯尔莫哥洛夫检验分布表Tab.2 The distribution forms of Kolmogorov test
3 舰船辐射噪声总声级和总能量的分布
根据上一节中的结论,可认为总声级多次测量值近似服从正态分布,代入样本数据,得到总声级X的概率密度函数为


表3 总声级取值区间概率大小Tab.3 Probablity of the total sound level span
从表3 中可以看出,总声级的取值主要集中在均值加减3 倍标准差之间。对于一个随机变量X,取完对数Y=lnX,如果Y 服从正态分布,那么X 服从对数正态分布[6]。这里,已经验证了总声级服从正态分布,而总声级为总能量取对数后的结果,因此,总能量服从对数正态分布。根据对数正态分布和式(1),得到总能量X′ 的概率密度函数为

其中:μ′=ln(10)/10* μ,σ′=ln(10)/10* σ。其概率密度函数曲线如图3所示。

图3 总能量取值分布Fig.3 Distribution of the total energy
从图3 可发现,总能量多次测量值的分布与某一正态分布相比,其概率密度函数不对称,概率密度函数左边上升较快,这与图2 中的结果类似。
4 结 语
在舰船辐射噪声总声级及总能量的统计分析研究中,根据舰船辐射噪声总声级和总能量多次测量值的直方图分布结果,假设该舰船辐射噪声总声级多次测量值满足正态分布,利用非参数假设检验中的皮尔逊χ2拟合检验和柯尔莫哥洛夫检验分别对其进行验证分析,结果表明总声级近似服从正态分布。然后根据总声级的分布,得出总能量服从对数正态分布,并分别给出它们的概率密度函数曲线。
[1]刘伯胜,雷家煜.水声学原理[M].哈尔滨:哈尔滨船舶工程学院出版社,1990.
LIU Bo-sheng,LEI Jia-yu.Water acoustics theory[M].Harbin:Harbin Ship Engineering Institute Press,1990.
[2]王之程,陈宗歧,于沨,刘文帅.舰船噪声测量与分析[M].北京:国防工业出版社,2004.
WANG Zhi-cheng,CHEN Zong-qi,YU Feng,Liu Wenshuai.Measurement and analysis of ship noise[M].Beijing:National Defence Industry Press,2004.
[3]吴翊,李永乐,胡庆军.应用数理统计[M].长沙:国防科技大学出版社,2008.
WU Yi,LI Yong-le,HU Qing-jun.Application of mathematical statistics[M].Changsha:National University of Defense Technology Press,2008.
[4]盛骤,谢式千,潘承毅.概率论与数理统计[M].北京:高等教育出版社,2008.
SHENG Zhou,XIE Shi-qian,PAN Cheng-yi.Probability and mathematical statistics[M].Beijing:Higher Education Press,2008.
[5]程兴新,曹敏,胡庆军.统计计算方法[M].北京:北京大学出版社,1989.
CHENG Xing-xin,CAO Min,HU Qing-jun.The statisticical calculation method[M].Beijing:Peking University Press,1989.
[6]刘东毅,马逢时,毛云英,史道济.科学计算与Matlab[M].北京:科技出版社,2001.
LIU Dong-yi,MA Feng-shi,MAO Yun-ying,Shi Dao-ji.Scientific computing and Matlab[M].Beijing:Science and Technology Press,2001.

