冲击荷载作用下船舶管路系统动力响应时域仿真分析及模型试验

嵇春艳，沈晴晴，于 雯，杨 苏

(江苏科技大学，江苏 镇江212003)

0 引 言

作为舰船生命力的重要组成部分，舰船内部复杂交错管路系统的抗冲击能力越来越受到关注。诸多战例和试验情况表明，舰艇遭受近距离水下爆炸冲击后，尽管船体结构完整，但许多舰艇系统设备却遭到功能性破坏，从而直接影响到其他设备、系统乃至舰艇的安全，因此管路系统的抗冲击性能显得尤为重要。

随着舰船设备的冲击理论研究、数学模型、计算方法及仿真研究等在不断发展完善，目前对设备的抗冲击分析经历了静态等效法、动态设计分析方法和时域模拟法3 个阶段。静态等效法只考虑了受冲击结构的质量效应，当一阶响应是设备的主要破坏因素时尚可用;动态设计分析方法用于分析舰船设备结构的最大线性动态响应，只能分析线弹性安装设备与设备线弹性破坏。而时域模拟法可采用实测的时间历程曲线，或标准的基础输入时间历程曲线作为设备的输入载荷，对设备进行瞬态动响应分析，可分析设备的非线性响应。开展舰船设备抗冲生命力的研究，最为准确可信的方法是进行实船水下爆炸试验。但是，实船水下爆炸试验费用昂贵，较为经济的数值试验方法受到广大发展中国家青睐。数值试验方法如何使计算模型更为接近真实物理模型，仿真结果如何提高计算精度历来是研究的难点和重点。

目前，国内关于舰艇管路系统的抗冲击研究还比较少，主要集中在理论及数值模拟方面。汪宏伟，汪玉等应用ANSYS—APDL 建立了某型艇动力装置管路系统的参数化模型，利用MATLAB 软件编制了程序对于管路系统冲击响应的灵敏度进行分析，该方法为管路系统抗冲击优化设计提供了依据［1］;李兆俊，汪玉分别采用等效静加速度法、动态设计分析法和设计谱法对管路系统进行抗冲击分析计算［2］;陈刚，汪玉等采用Sobol′法对半正弦冲击载荷作用下二维的管路系统材料弹性模量、密度，管壁厚、内径，以及支承刚度及位置，冲击作用间隔时间等参数进行了全局灵敏度分析，得出了单个或多个参数联合对管路系统冲击位移动响应的影响［3］;郭晋挺，司马灿等对舰艇管路系统的抗冲击性能进行了研究［4］。

本文基于时域分析法，分别采用接触单元、固定约束单元模拟管夹、支吊架管路元器件对管路系统的约束，建立冲击荷载作用下管路系统的时域仿真计算分析方法，并通过典型船舶管路段跌落台物理模型试验对上述仿真方法进行有效修正和验证，通过模型试验验证，本文给出的仿真分析方法仿真精度与试验结果相比，峰值误差小于15%。

1 管路系统动力响应时域仿真分析方法

在进行结构动力响应分析时，建立数学模型通常有3 种方法:集中质量法，广义坐标法和有限元法。实际的海洋平台结构较为复杂，在计算分析时，本文采用精度较高的有限元法。

考虑将管路离散为具有n 个自由度的有限元系统。管路结构运动方程可以表示为:

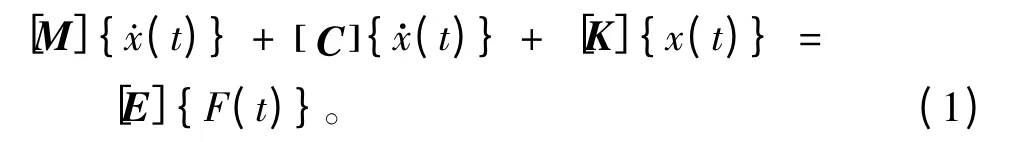
关于在时域求解如式(1)所表述平台的振动方程一般可以采用2 类方法，一类是直接积分法，就是按时间历程对上述微分方程直接进行数值积分，即数值解法。常用的数值解法有中心差分法、纽马克法和威尔逊θ 法;另一类是模态(振型)叠加法。如采用中心差分法求解平台的时域动力响应。

2 典型管路段冲击试验设计

2.1 试验设计

试验使用上海交通大学的振动冲击平台，平台尺寸为1.2 m×1.2 m，管路参考实船动力机舱中海水管路中典型段按1:10 比例设计，为了充分利用冲击平台的尺寸，管路设计水平长1.2 m，直径20 mm，壁厚4 mm，包括6 个弯头，1 个法兰连接件。管路与冲击平台通过槽钢进行固定，槽钢与管路之间通过4 个管夹支撑，如图1所示。测试系统主要包括，冲击试验台1 个，加速度传感器4 个，信号分析仪1 台，电荷放大器2 台，信号发生器1 台。测点布置如图2所示。

试验冲击工况共4 种，振动台跌落高度依次为100 mm，110 mm，120 mm，130 mm。通过冲击试验记录4 个测试点在4 种工况下的实验数据，以便于仿真模型结果比较。

图1 管路系统管夹位置Fig.1 Position of clap of pipeline system

2.2 冲击载荷

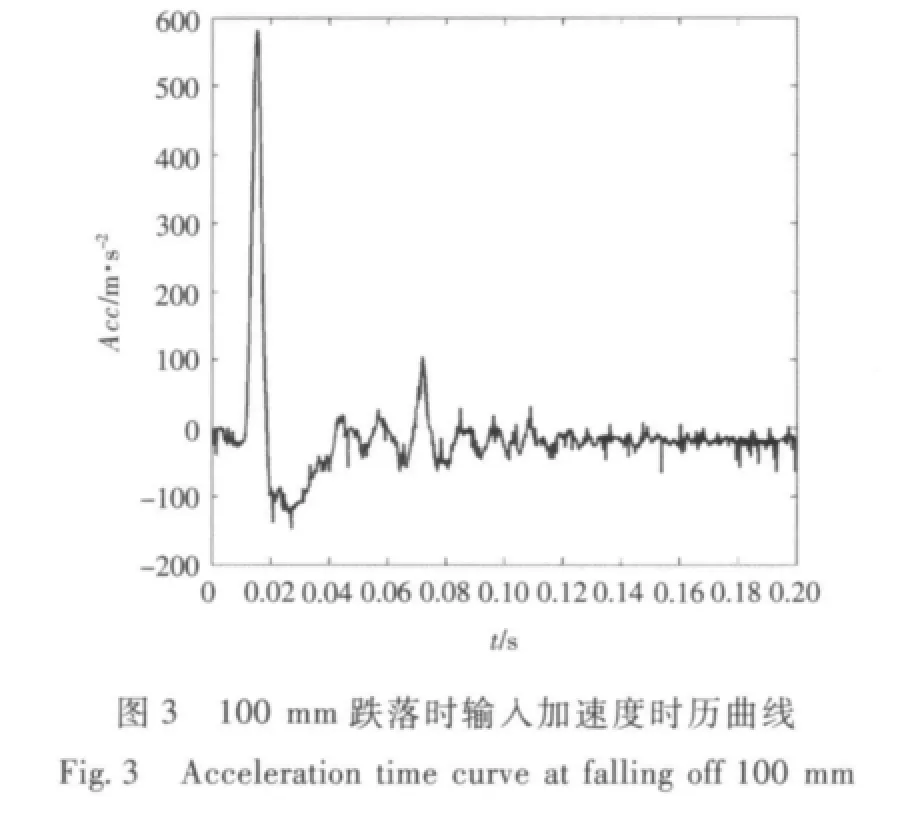
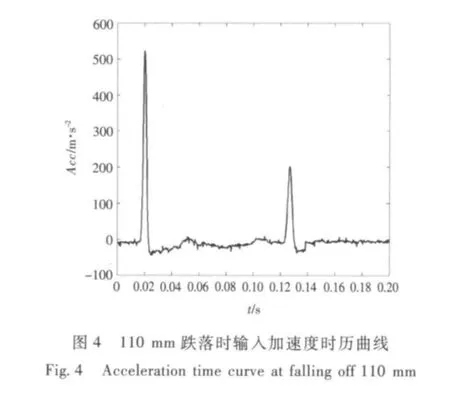
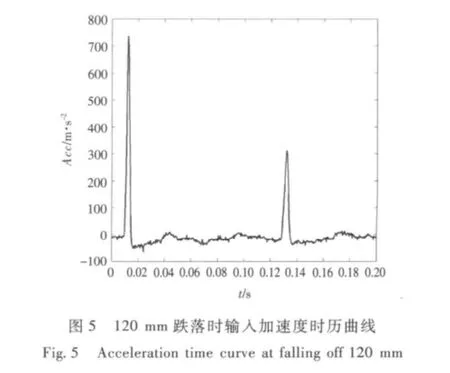
试验过程中的加速度响应信号为振动台面的加速度响应信号，试验台的加速度通过与管路两端的固定连接部位输入管路，从而模拟管路受冲击下的动力响应。在数值模拟中采用施加整体加速度的方法输入试验过程中的加速度响应信号来模拟冲击输入。试验测得的跌落时输入加速度响应如图3 ～图6所示，数值模拟过程中将该加速度响应以加速度的输入方式作为荷载输入。

图2 加速度传感器测试位置Fig.2 Position of acceleration transducer

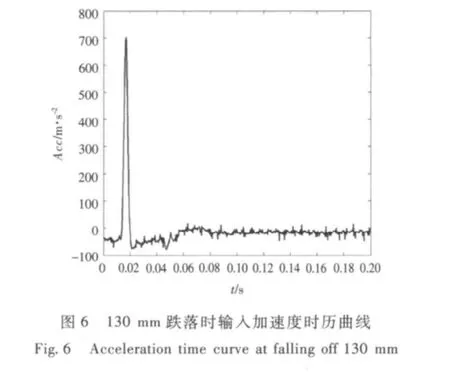
3 模型数值仿真及试验结果对比分析

3.1 典型管路系统及元器件建模

采用ANSYS10.0 软件建立试验管路冲击模型，采用自下而上的实体建模技术，分别采用壳单元划分管路、体单元划分试验管夹，共划分16 387 个单元，9 557 个节点。为了保证数值模拟的计算精度，同时提高计算效率，对于管夹与管路之间的连接分别采用接触单元及刚性位移固定处理，比较2 种边界条件下数值模型计算结果。图7 为使用接触单元处理管路与管夹连接的有限元模型。图8 为使用刚性固定方式处理管路与管夹连接的有限元模型。

3.2 两种约束条件下数值模拟结果对比

接触约束可以较好地反应管路与管夹及支吊架的约束情况，但计算非常耗时;位移约束对管夹约束和支吊架约束进行了简化处理，计算效率高，耗时少。因此为了既能保证计算精度又能提高计算效率，本项目对2 种约束情况下4 种冲击工况下的动力响应进行了仿真，分别对4 种工况下2 种不同边界处理方式进行比较，图9 为工况为120 mm 跌落下位移约束与接触约束结果对比。

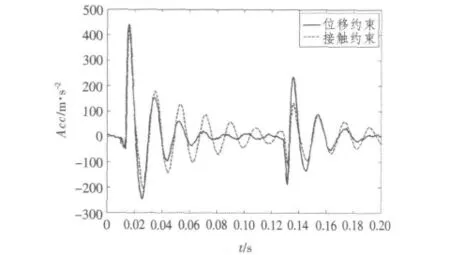
图9 120 mm 通道2 位移约束和接触约束对比图Fig.9 Comparison between displacement constraint and contact constraint at falling off 120 mm

对4 种工况比较结果可以看出，2 种约束处理情况的计算结果非常接近，因此为了提高计算效率，采用位移约束的处理方式进行数值仿真分析。

3.3 数值模拟结果与实验结果的对比分析

分别对有限元模型输入4 种获得的加速度响应，依次获取通道2、通道3 及通道4 的数值模拟结果，图10 ～图13 分别为从100 mm，110 mm，120 mm 及130 mm 高度跌落时通道2 试验数据和模拟数据的对比图。表1 ～表3 分别为通道2、通道3 及通道4 数值模拟结果和实验所得结果对比数据。

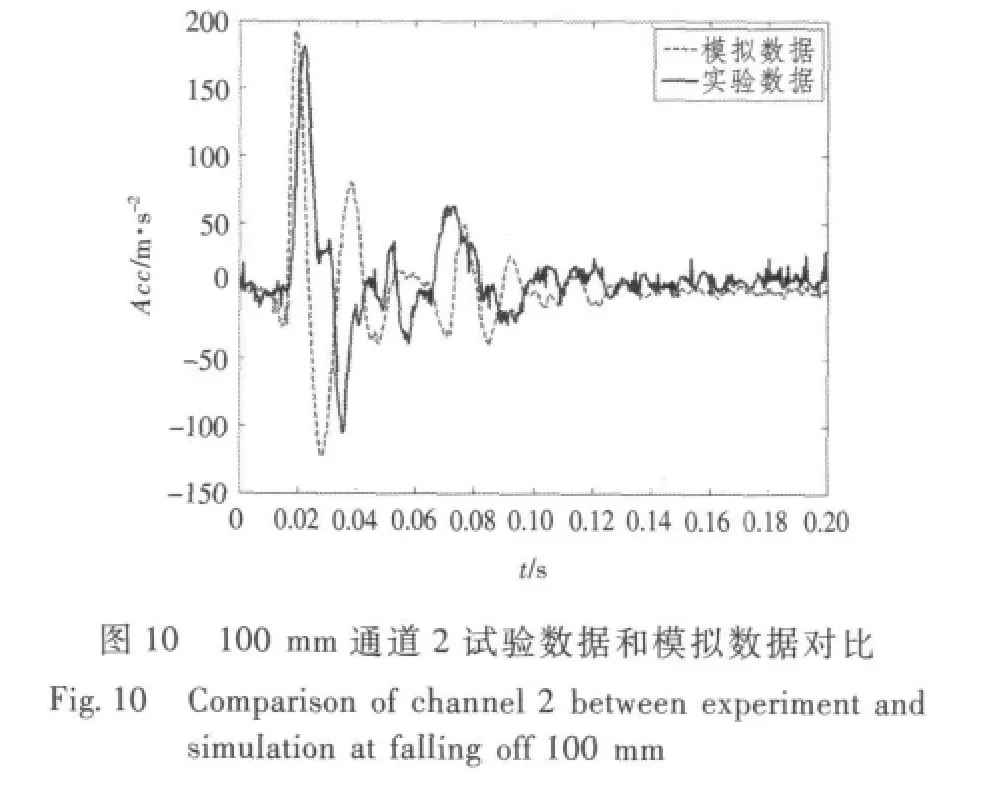
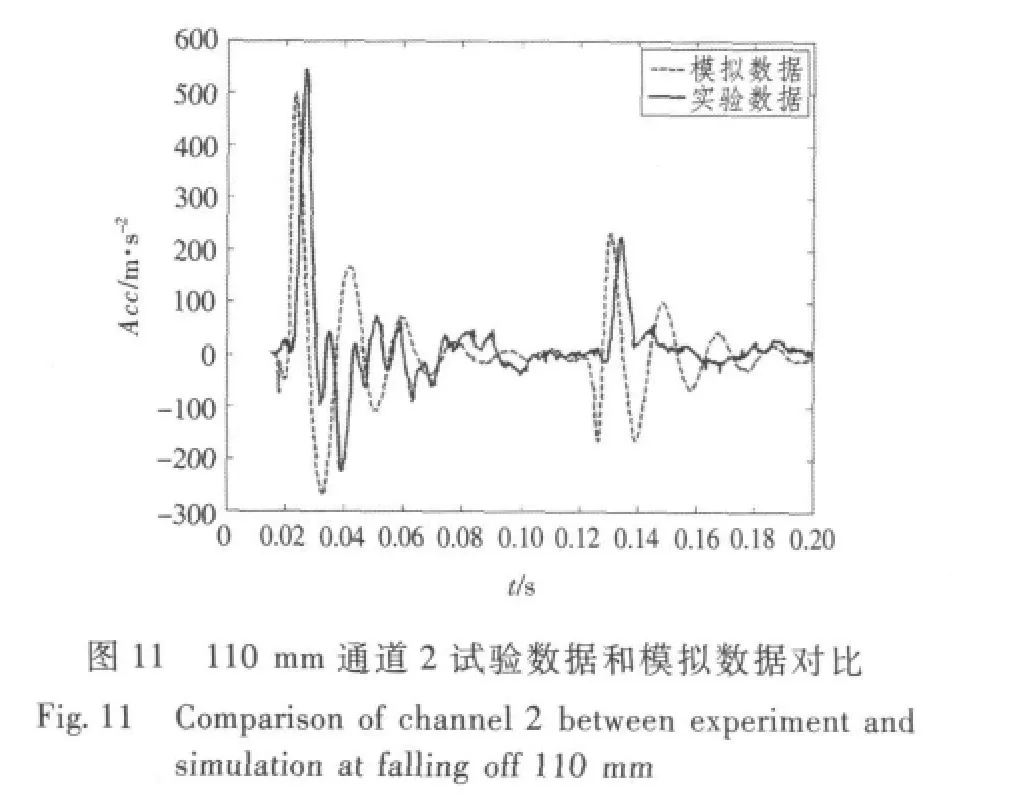
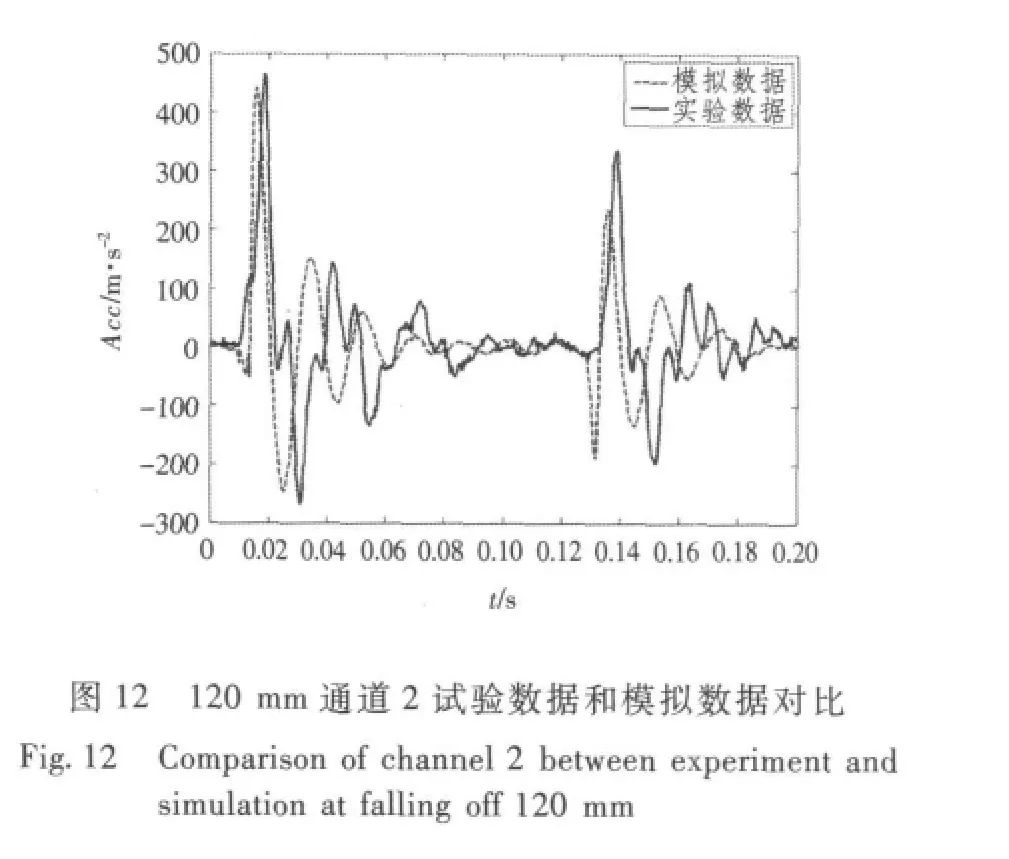
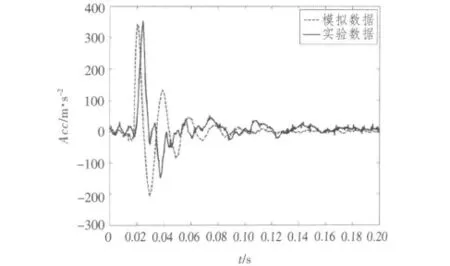
图13 130 mm 通道2 试验数据和模拟数据对比Fig.13 Comparison of channel 2 between experiment and simulation at falling off 130 mm

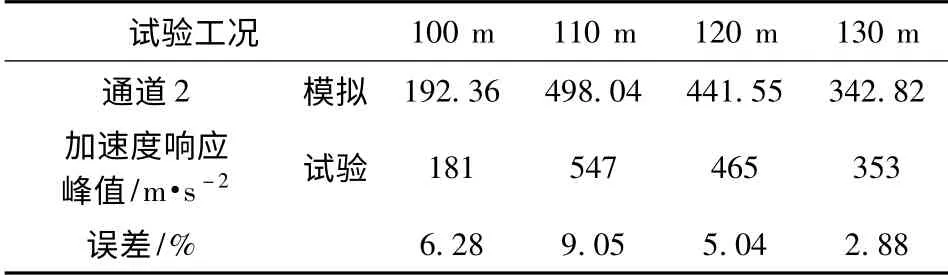
表1 通道2 数值模拟结果和实验所得结果数据对比Tab.1 Comparison of channel 2 between result of experiment and simulation

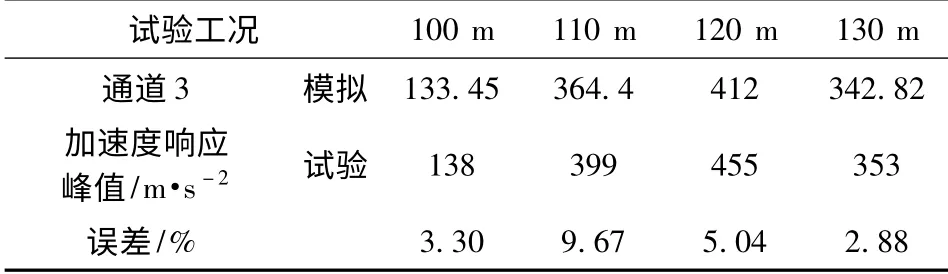
表2 通道3 数值模拟结果和实验所得结果数据对比Tab.2 Comparison of channel 3 between result of experiment and simulation

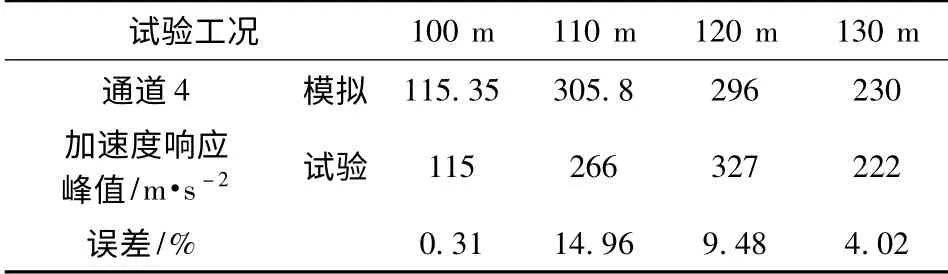
表3 通道4 数值模拟结果和实验所得结果数据对比Tab.3 Comparison of channel 4 between result of experiment and result of simulation

从表1、表2 及表3 中数值仿真试验结果和试验所得结果数值比较可知，误差均小于15%，因此采用该时域方法对管路系统抗冲击性能进行计算是可行性的，并且能保证计算精度。

4 结 语

本文在管路冲击试验的技术上，基于多点时域分析方法及ANSYS 仿真软件，对数值仿真模型边界条件及安装因素不断修正，找出一种与试验结果误差小于15%的数值仿真计算方法。对管路系统模拟过程中管路与连接件之间2 种处理方式进行比较，大大减少了计算时间。本文为管路系统抗冲击数值仿真研究提供了新的思路，为系统研究管路系统的抗冲击性能提供了方便。

［1］汪宏伟，汪玉，赵建华.EFAST 法在管路系统冲击响应中的应用研究［J］.振动与冲击，2010，29(4):197-199.

WANG Hong-wei，WANG Yu，ZHAO Jian-hua.Application of extended Fourier amplitude sensitivity test method in shock response of a piping system［J］.Journal of Vibration and Shock，2010，29(4):197-199.

［2］李兆俊，汪玉，陈学德，等.管路系统冲击设计方法分析［J］.振动与冲击，2008，27(9):171-174.

LI Zhao-jun，WANG Yu，CHEN Xue-de，et al.Analysis for pipeline system shock design methods［J］.Journal of Vibration and Shock，2008，27(9):171-174.

［3］陈刚，汪玉，毛为民，等.冲击载荷作用下舰艇管路系统全局参数灵敏度分析［J］.振动与冲击，2007，26(3):45-48.

CHEN Gang，WANG Yu，MAO Wei-min，et al.Gloabl parameter sensitivity analysis of shipboard piping systems under shock loads［J］.Journal of Vibration and Shock，2007，26(3):45-48.

［4］郭晋挺，司马灿，刘建湖，等.舰艇管路系统的抗冲击性能弹性评估方法［J］.船舶力学，2004，8(4)108-115.

GUO Jin-ting，SIMA Can，LIU Jian-hu，et al.A evaluation method for the anti-shock strength safety of shipboard pipelines in elastic domain［J］.Journal of Ship Mechanics，2004，8(4):108-115.

［5］姚熊亮，冯麟涵，张阿漫.舰船设备抗冲击时域模拟研究［J］.汽轮机技术，2009，52(3):190-194.

YAO Xiong-liang，FENG Lin-han，ZHANG A-man.Antishock simulation of equipments on board in time-domain［J］.Turbine Technology，2009，52(3):190-194.

［6］赵应龙，何琳，黄映云，等.船舶浮筏隔振系统冲击响应的时域计算［J］.噪声与振动控制，2005，(2):14-17.

ZHAO Ying-long，HE Lin，HUANG Ying-yun，et al.Thc computation of shock response of marine floating raft shockresistant system in the time domain［J］.Noise and Vibration Control，2005，(2):14-17.

［7］周其新，姚熊亮，张阿漫.舰用齿轮箱抗冲击能力时域计算［J］.中国舰船研究，2007，2(3):44-48.

ZHOU Qi-xin，YAO Xiong-liang，ZHANG A-man，et al.Anti-shock performance analysis of marine gear case by time domain calculation［J］.Chinese Journal of Ship Research，2007，2(3):44-48.