圆锥壳和圆柱壳声辐射模态特性比较

张晓宇，陈美霞，魏建辉

(华中科技大学，湖北 武汉430074)

0 引 言

对于弹性体的振动研究，例如一块板在简谐力的作用下振动，其结构模态下每一阶的辐射声功率并不是相互独立的，在中低频的情况下，即使降低了最主要的几阶结构模态的振动，其总的辐射声功率并不一定会降低。随着振动问题研究的日趋成熟，人们开始意识到直接用振动结构模态来研究声辐射问题存在不少的缺陷，因此有必要发展一种适用于声辐射问题的模态。

20世纪90年代开始，Borgiotti［1］，Curfare［2］，Elliott［3］，Baumann［4］，Synder［5］等首先提出了声辐射模态的概念。声辐射模态表示结构的固有辐射特性，是结构表面可能的一系列振速分布。根据声辐射模态方法，弹性结构总的辐射声功率可以看作有限个辐射模态的叠加，用声辐射模态研究声辐射问题的优点在于消除了结构模态中复杂的耦合项，使得计算和控制声辐射更为简单。李双和陈克安［6］对结构振动模态和声辐射模态之间的对应关系做了研究，给出了主导辐射模态的概念。姜哲［7-8］提出了对声辐射模态的改进方法，对平板的主动控制进行了深入研究。吴卫国［9］等基于远场的方法，研究了圆板和矩形板的声辐射模态特性。代路［10］等采用单元辐射器法和基函数法，研究了球形和圆柱形结构的声辐射模态特性。

单层加筋圆柱壳和圆锥壳是舰艇中的主要结构形式，比较研究二者声辐射模态特性的相关文献还不是很多，本文以有限元法和边界元法为指导，对尺寸相近的圆柱壳和圆锥壳的声辐射模态特性进行研究，对于其振动和噪声的有源控制提供了一定的参考和建议。

1 声辐射模态基本理论

把结构表面分成面积相等的N 个面元，各个面元的表面声压构成列向量P，面元的法向速度构成向量v，则P=Zv。其中Z 表示声阻抗矩阵，根据互易性原理，Z 是对称矩阵，即Z=ZT。

则结构的辐射声功率为

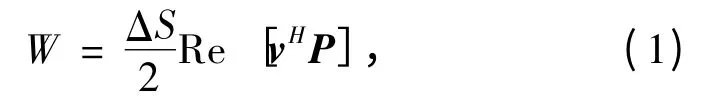
“H”表示共轭转置。将P=Zv 代入式(1)得:

由于声场的互易性，R 为对称矩阵，又因为辐射声功率恒为正，所以R 为正定的对称矩阵。矩阵R 可以作如下的特征值分解:

式中:Λ 为矩阵R 的特征值λk(k=1，2…，N)构成的对角阵(根据正定矩阵的性质，故λk均为正数。);Q 为R 矩阵的特征向量qk(k=1，2…，N)构成的矩阵。

则辐射声功率为:

式中:Q 的列向量表示结构表面可能的振速分布，称为声辐射模态;加权系数λk为矩阵R 的第k 阶特征值，称为第k 阶声辐射模态的辐射效率系数。

声辐射模态辐射效率可定义为:

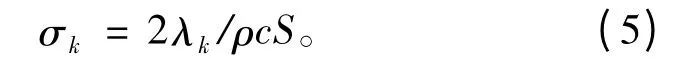
式中:ρ 为流体介质密度;c 为流体介质中的声速;S为结构的表面积。

由式(4)可知，各阶声辐射模态对辐射声功率的贡献是独立的，所以降低声辐射模态一定可以减小辐射声功率。由于辐射阻抗矩阵R 只与结构的形状、尺寸和激励频率有关，所以声辐射模态也仅仅与结构形状、尺寸和激励频率相关。

2 算例分析

本文的研究对象为单层加筋圆锥壳和圆柱壳。圆锥壳小圆半径r=1.25 m，大圆半径R=4 m，长L=9.6 m，厚度d=0.03 m，肋距为0.6 m，肋骨为T 型材。圆柱壳圆半径为R1=4 m，其他尺寸跟圆锥壳相同。结构材料属性:密度为7 850 kg/m3，杨氏模量E=210 GPa，泊松比μ=0.3。流体属性:密度为1 000 kg/m3，声速为1 500 m/s。

2.1 声辐射模态辐射效率比较

在用边界元方法计算该单层壳的声阻抗矩阵时，由于两端处节点的法向不好确定，所以采用延长肋位的方法，先将两端分别延长2 个肋位，然后对计算出的结果只取有用节点处的值即可计算频率为10 ～600 Hz，频率间隔为10 Hz。圆柱和圆锥的有用节点数都为1 584 个，其边界元模型如图1所示。

图1 边界元模型Fig.1 Boundary element model

绘制前10 阶声辐射模态的辐射效率随着激励频率的变化曲线，如图2所示。

由图2 可知，不论是圆柱壳还是圆锥壳，其辐射效率曲线的趋势都是一样的:对于每一阶声辐射模态，辐射效率都是随着频率的升高而升高，最后曲线会逐渐趋于平缓。声辐射模态的一个重要特点是在中、低频段声辐射模态对应的辐射效率随着阶数的增加急剧降低，因此在中、低频段根据式(4)计算结构的辐射声功率时，只需要通过测量数据得到前几阶声辐射模态参与系数就可以较准确地得出壳体的辐射声功率。进行主动控制时，只需要考虑前几阶声辐射模态就可以了。本文界定前10 阶声模态辐射效率占主导地位时的频率为f0，也就是在f0的范围内，利用前10 阶声辐射模态计算辐射声功率就可以有很好的精度;对于前10 阶声模态进行控制就可以达到很好的降噪效果。

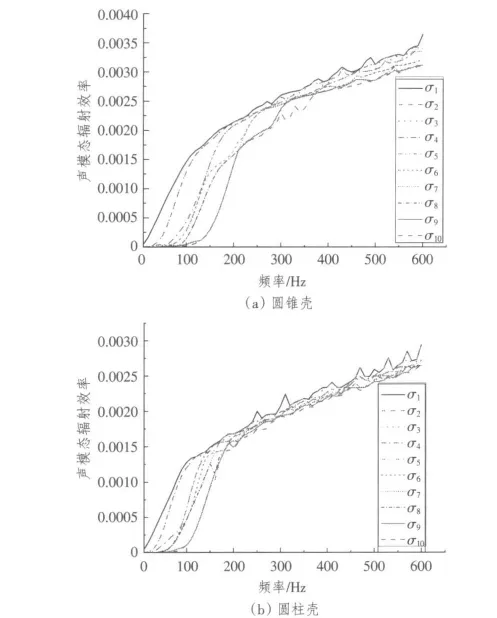
图2 声模态辐射效率曲线Fig.2 Acoustic modes radiation efficiency curve

分别观察圆锥壳和圆柱壳每一频率下辐射效率随阶数的变化，找出各自的频率f0如图3所示。

由图3 可以看出，圆锥壳的频率f0比圆柱壳的频率f0要大一些，对于本文中的圆锥壳和圆柱壳而言，各自的频率f0分别为120 Hz 和80 Hz。也就是说，相同尺寸的圆锥壳声模态辐射效率随阶数的衰减要比圆柱壳的衰减快。

分别取圆锥壳和圆柱壳的前6 阶声模态辐射效率，在此中、低频段进行比较，如图4所示。

由图4 可以看到，在本文研究的中、低频段，圆锥壳和圆柱壳的辐射效率曲线走向趋势是一致的。对于第一阶声模态，在整个频段内圆锥壳的辐射效率都高于圆柱壳的辐射效率;对于第二、三阶声模态，在0 ～90 Hz 圆柱壳辐射效率高于圆锥壳辐射效率，但二者差别不是很大，90 ～600 Hz 圆锥壳辐射效率高于圆柱壳的辐射效率;对于第四、五阶声模态，在0 ～150 Hz 圆柱壳辐射效率高于圆锥壳辐射效率，但二者差别不是很大，150 ～600 Hz 圆锥壳辐射效率高于圆柱壳的辐射效率;对于第六阶声模态，在0 ～170 Hz 圆柱壳辐射效率高于圆锥壳辐射效率，但二者差别不是很大，170 ～600 Hz 圆锥壳辐射效率高于圆柱壳的辐射效率。这里的辐射效率是根据式(5)计算的，其中辐射效率系数来自声辐射阻抗矩阵的特征值分解，本来圆柱壳的表面积要比圆锥壳的表面积大，但是此声阻抗矩阵是与表面形状、尺寸和激励频率密切相关的，所以二者的辐射效率曲线会如此变化。并且随着阶数的增加，频率转折点的值越来越大。

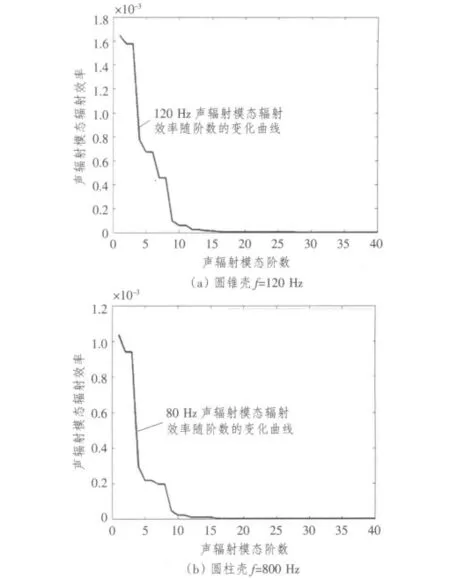
图3 辐射效率随阶数的变化Fig.3 Radiation efficiency changes with the order

2.2 声辐射模态形状比较

声辐射模态有一个重要的性质，那就是在中、低频段，声辐射模态的形状随着频率的变化差别不大。本文分别取圆锥壳和圆柱壳各自特征频率下的前6 阶声辐射模态云图进行比较，如图5 ～图10所示。

对于声辐射模态，采用m 表示轴向半波数，n 表示周向波数，将以上云图结果归纳到如表1所示。

对于圆锥壳和圆柱壳来说，声辐射模态的振速分布都是一样的:第一阶为轴向和周向都分布均匀的活塞状模态，此辐射效率最高;第二、三阶为轴向均匀、周向对称的偶极子模态;第四阶为分布均匀的轴向偶极子模态;第五、六阶为周向四极子模态。对于圆锥壳和圆柱壳这2 种形状相近的回转体来说，其声辐射模态有着一样的规律，在主动控制的时候可以归为一类来考虑。

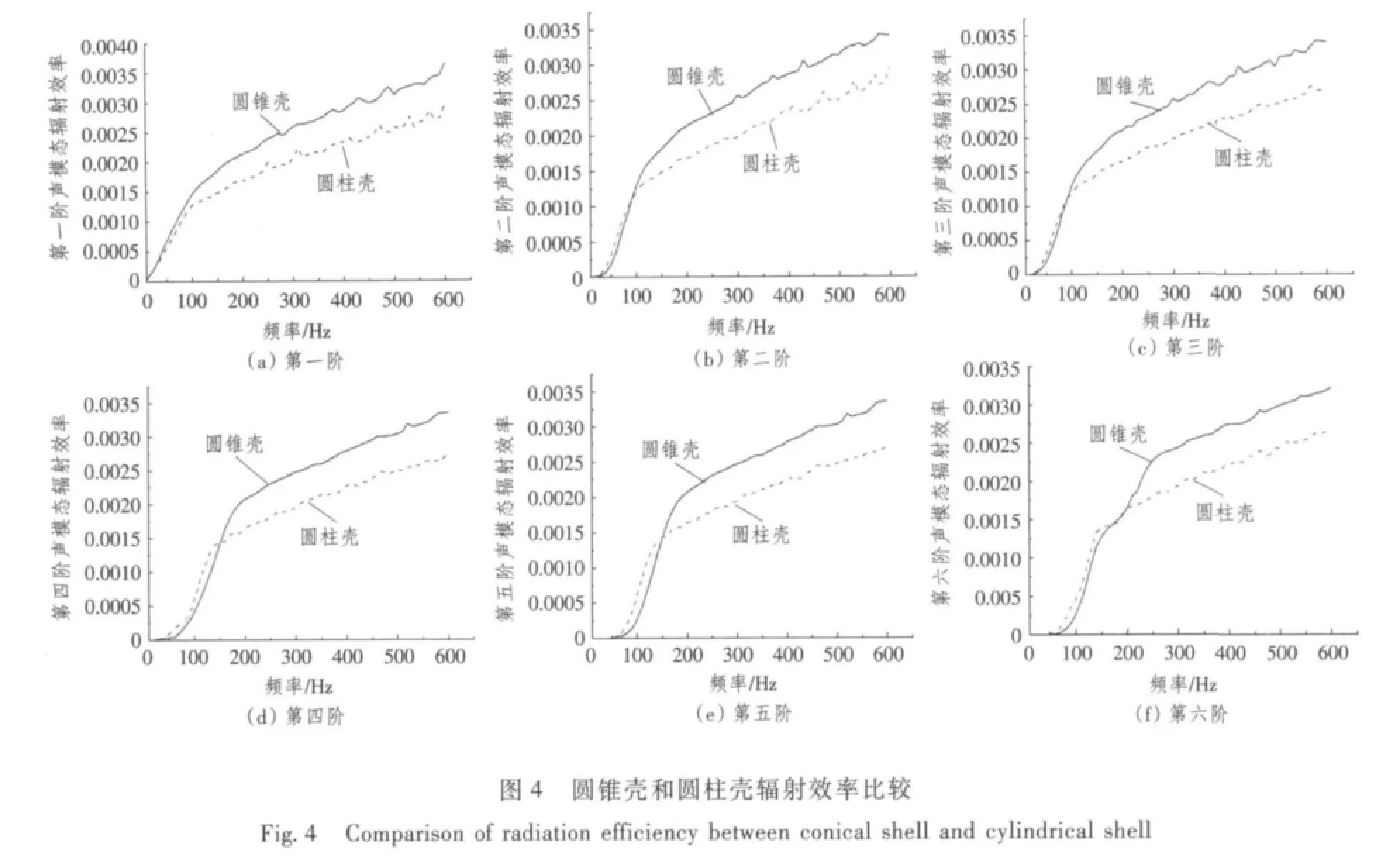
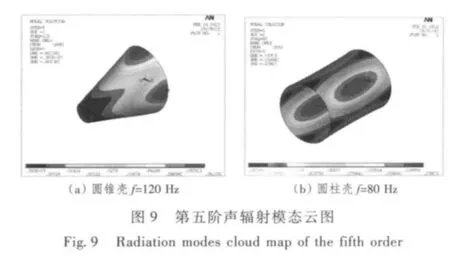
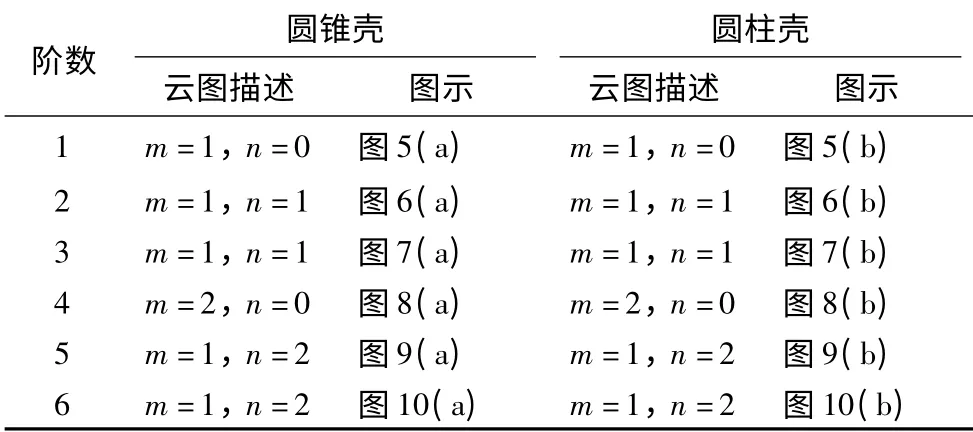
表1 圆锥壳和圆柱壳前6 阶声辐射模态形状比较Tab.1 Comparison of the first 6 acoustic modes shapes between conical shell and cylindrical shell

3 结 语

本文采用有限元法和边界元法的理论，在中、低频段对比了水中单层加筋圆锥壳和圆柱壳的声辐射模态特性，得出以下结论:

1)对于相同尺寸的圆锥壳和圆柱壳而言，二者的声模态辐射效率曲线走势都是一样的，圆锥壳前10 阶模态占主导地位时的频率f0高于圆柱壳的f0，圆锥壳辐射效率随着阶数的衰减要比圆柱壳的衰减更快;

2)在本文研究的中、低频段范围内，对于每一阶声模态而言都存在一个频率转折点。低于该频率时，圆柱壳的辐射效率高于圆锥壳的辐射效率，但二者相差不是很大;高于该频率时，圆锥壳的辐射效率高于圆柱壳的辐射效率。并且随着阶数的增加，该频率转折点的值越来越大;

3)圆锥壳和圆柱壳的声辐射模态振速云图分布都遵循一样的规律，为壳体的主动控制研究提供了一些参考。

［1］BORGIOTTI G V.The power radiated by a vibrating body in an acoustic fluid and its determination from boundary measurements［J］.Journal of the Acoustical Society of America，1990，88(4):1152-1159.

［2］CUNEFARE K A.The minimum multimodal radiation efficiency of baffled finite beams［J］.Journal of the Acoustical Society of America，1991，90(5):2521-2529.

［3］ELLIOTT S J，JOHNSON M E.Radiation modes and the active control of sound power［J］.Journal of the Acoustical Society of America，1993，94(4):2194-2204.

［4］BAUMANN W T，SAUNDERS W R，et al.Active supperession of acoustic radiation from impulsively excited structures［J］.Acoust.Soc.Am，1991，88(6):3202-3208.

［5］SNYDER S D，TANAKA N.On feedforward active control of sound and vibration using vibration error signals［J］.Acoust.Soc.Am，1993，94(4):2181-2193.

［6］李双，陈克安.结构振动模态和声辐射模态之间的对应关系及其应用［J］.声学学报，2007，32(2):171-177.

LI Shuang，CHEN Ke-an.The relationship between acoustic radiation modes and structural modes and its applications［J］.Acta Acustica，2007，32(2):171-177.

［7］姜哲.声辐射问题中的模态分析:Ⅰ理论［J］.声学学报，2004，29(4):373-378.

JIANG Zhe.A model analysis for the acoustic radiation problems:ⅠTheory［J］.Acta Acustica，2004，29(4):373-378.

［8］姜哲.声辐射问题中的模态分析:Ⅱ实例［J］.声学学报，2004，29(6):507-515.

JIANG Zhe.A model analysis for the acoustic radiation problems:ⅡExamples［J］.Acta Acustica，2004，29(6):507-515.

［9］吴卫国，王贵成，马利杰.基于远场方法的结构声辐射模态研究［J］.应用基础与工程科学学报，2006，14(1):94-99.

WU Wei-guo，WANG Gui-cheng，MA Li-jie.Analysis of acoustic radiation modes by far field method［J］.Journal of Basic Science and Engineering，2006，14(1):94-99.

［10］代路，杨铁军，杜敬涛，靳国永，率志军.球形和圆柱形结构的声辐射模态及特性分析［J］.船海工程，2009，38(5):66-70.

DAI Lu，YANG Tie-jun，DU Jing-tao，JIN Guo-yong，SHUAI Zhi-jun.Acoustic radiation modes and characteristic analysis of spherical and cylindrical structure［J］.Ship and Ocean Engineering，2009，38(5):66-70.