查询RLC电网络中“独立”全电容割集的算法研究＊

高国章 劳 深

（武汉理工大学能源与动力工程学院1） 武汉 430063） （武汉理工大学国际教育学院2） 武汉 430063）

0 引 言

利用状态方程分析电网络的结构性质［1］时，常常要用到系数矩阵A．文献［2］中已经证明，在多元有理函数域F（z）上，A的特征根可能是“0”或者不相等的非常数根．根据电网络理论，当A有“0”根时，表明网络中有全电容割集（包括电容电流源割集）和或者全电感回路（包括电感电压源回路）．

众所周知，全电容割集和全电感回路并不改变网络的复杂度（N）．一个网络的非零特征根的个数（N－（NL＋NC））等于网络的复杂度减去网络中“独立”的全电容割集数（NC）和全电感回路的个数（NL）的和．那么该如何去查寻一个网络中有多少个“独立”的全电容割集和全电感回路呢？对于一个复杂的网络来说显然人工难以去确定．如果利用计算机来完成，则需要确定一个算法．本文主要讨论查寻网络中“独立”的全电容割集的算法．

在讨论之前，先给出下文中要利用的关于“环和”的定义．

定义 设S，S1，S2是3个集合，且S＝｛S1－（S1∩S2）｝∪｛S2－（S1∩S2）｝，那么称S 为S1和S2的“环和”，记为：S＝S1⊕S2．

根据文献［3－4］确定电网络的全部割集可以采用如下步骤：（1）确定网络的一棵正则树；（2）确定每条树支所对应的基本割集矩阵Qf；（3）对Qf中的行向量执行所有的环和；（4）消除环和所产生的冗余行向量，即得到Qa．

很显然，全电容割集也是网络所有割集中的一部分，所以它们所对应的集合也对应着Qa中的某些行向量，但是它们所对应的全电容割集并不都是我们所要寻找的“独立”的割集．

1 电网络中全电容割集的确定方法

对于已经找出的网络中的所有割集，“独立”的全电容割集及其数目可以按如下步骤搜寻．

步骤1 确定网络的一颗正则树．

步骤2 写出每一个树支电容所对应的基本割集矩阵Qfcap．

假定网络中有m个树支电容SBCap＝｛Ct1，Ct2，…，Ctm｝，它们所对应的基本割集分别Cut1，Cut2，…，Cutm．这些基本割集中，有些可能是全电容割集，有些则可能不是，具体见下文的实例分析中．

步骤3 判断全电容割集 一般地，电容电流源割集也包含在全电容割集中．根据前面割集集合的寻找方法，全电容割集的集合应该由两部分组成，一部分是树支电容所对应的基本割集，另一部分是由树支电容所对应的基本割集环和产生，所以Cut1，Cut2，…，Cutm中包含了第一部分．为了找出全部的全电容割集，这一步中应完成如下工作：

1）对Cut1，Cut2，…，Cutm，判断每一个割集中的元素，若它们都是电容或者电流源，则该基本割集就是一个全电容割集（即单树支电容的割集）；否则不是．假设其中有p个这样的全电容割集，分别记为：Cut1，Cut2，…，Cutm（0≤p≤m）；

2）对Cut1，Cut2，…，Cutm执行所有的环和，即先取任意2个求环和，然后取3个求环和，如此直至取m个求环和，并判断，因此总的求环和的次数为＋＋…＋＝2m－1－m（m≥2）．记某次求环和所得到的集合为Ssum＝Cuti⊕Cutj⊕…⊕Cutk．其中（0＜i，j，k≤m，i≠j≠…≠k），若Ssum＝Cuti⊕Cutj＝Cuti∪Cutj，则Ssum为冗余项，则消除，说明本次环和所得到的新集合不是一个割集，它也不属于Qa，即Ssum∉Qa；否则，Ssum∈Qa．记所有属于Qa的割集集合为：CSsumc1，CSsumc2，…，CSsumcr．显然r小于等于Qa的维数．也就是说，含有树支电容的割集除了Cut1，Cut2，…，Cutm以外，还有CSsumc1，CSsumc2，…，CSsumcr，但这些割集并不都是全电容割集．

3）判断CSsumc1，CSsumc2，…，CSsumcr是否是全电容割集．任取其中一个割集CSsumci（0≤i≤r），判断CSsumci的元素是否都是电容或者电流源，若是，则该割集为全电容割集；否则不是．记其中的全电容割集为ACSsumc1，ACSsumc2，…，ACSsumcq（0≤q≤r）．

4）网络中的全电容割集为：ACC＝｛Cut1，Cut2，…，Cutp，ACSsumc1，ACSsumc2，…，ACSsumcq｝，其数目为：Nacc＝p＋q，但是，Nacc并不是网络中“独立”的全电容割集数．

2 电网络中“独立”的全电容割集及其数目

对于已经搜寻出的网络中所有的全电容割集，它们并不是每一个都是“独立”的．重记ACC中的每一集合，令：Acc1＝Cut1，Acc2＝Cut2，…，Accp＝Cutp，Accp＋1＝ACSsumc1，…，Accp＋q＝ACSsumcq，则：ACC＝｛Acc1，Acc2，…，Accp＋q｝．

从某种程度上说，ACC中每一个集合都是“独立”的，但它们的“独立”性具有一定的相对性．比如，假设Accj∈ACC（j＝1，2，3），但是Acc3＝Acc1⊕Acc2，那么可以认为其中的任意2个都是独立的，另外一个可由其他2个求“环和”得到．根据KCL定理，每一个割集都对应一个方程，那么ACC就对应了一个方程组．这些割集不是“独立”的原因，是因为方程组中的某些方程可以由其他的几个方程通过线性变换得到，所以寻找独立的割集过程也就是消除方程组的相关性的过程．当消除相关性以后，剩下的方程的个数，就是“独立”的割集的个数．很显然，仍然可以通过求环和的方法来消除这些多余的割集（也就是多余的方程）．令网络中"独立"的全电容割集个数为Nindac，非“独立”的个数为K，这个过程可按如下步骤进行．

步骤1 先取出Acc1分别与Acc2，…，Accp＋q两两求环和．令K＝0，RN＝2．p＋q＝RN吗？若是，则程序结束；否则往下执行．假设记：Set＝Acc1cct（2≤t≤p＋q），若Set∈ACC，则Set是一个割集，假设为Accj（3≤j≤p＋q），但它是非“独立”的，消除它，程序中可将该集合的元素全部置“0”的方法来标记，同时K＝K＋1；否则，t＝t＋1，且Acc1不再与Accj求环和．

步骤2 对ACC中的剩下的非“0”向量每3个求环和．RN＝RN＋1，RN＝p＋q－K 吗，若是，则程序结束；否则继续．同步骤1一样，如果环和所得到的集合仍为一个属于ACC的元素，则消除它．

…

假设经过这样的消除过程以后，ACC中的剩下的非“0”元素为（p＋q－K）个．

（p＋q－K－1） 在剩下的（p＋q－K）个非“0”集合中取（p＋q－K－1）个求环和．RN＝RN＋1，RN＝p＋q－K 吗，若是，则程序结束；否则继续．执行类似消除过程．

（p＋q－K） RN＝RN＋1，RN＝p＋q－K吗，若是，则程序结束；否则继续．结束程序．记录ACC和K，则可将ACC中的集合中的“非”零的集合，作为“独立”的全电容割集．其个数为：Nindac＝p＋q－K．

3 应用实例

考虑如图1所示的电网络．

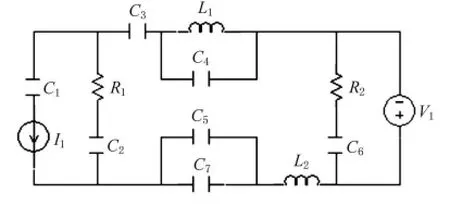
图1 电网络

按前文的算法，文献［1，4］中提到作者所在的课题组已经开发了一个分析电网络的软件［5－7］，利用该软件不难得到一颗正则树，同时得到树支中的电容集合．如图1软件选择C1，C2，C3，C4，C5，C6，R1，V1为树枝，则上文中的步骤如下．

1）选定正则树和确定树支电容集合 令选取的树支中电容集合为SBCap＝｛C1，C2，C3，C4，C5，C6｝．

2）找出树支电容所对应的基本割集 Cut1＝｛C1，I1｝，Cut2＝｛C2，I1，L2｝，Cut3＝｛C3，L2｝，Cut4＝｛C4，L1，L2｝，Cut5＝｛C5，C7，L2｝，Cut6＝｛C6，R2｝．

3）确定全电容割集 对Cut1，Cut2，…，Cut6执行所有的环和，共执行26－1－6＝57次．限于篇幅，这里不列出所有的环和结果，这里只列出Step1－3－4的结果，也就是网络中所有的全电容 割 集，ACC ＝ ｛Cut1，ACSsumc1，ACSsumc2，ACSsumc3，ACSsumc4，ACSsumc5｝，其中 Acc1＝Cut1＝｛C1，I1｝，Acc2＝ ACSsumc1＝｛C2，C3，I1｝，Acc3＝ ACSsumc2＝ ｛C2，C5，C7，I1｝，Acc4＝ACSsumc3＝｛C3，C5，C7｝，Acc5＝ ACSsumc4＝｛C1，C2，C3｝，Acc6＝ ACSsumc5＝｛C1，C2，C5，C7｝，所以程序执行到此，可以知道，p＝1，q＝5．接下来，找出这些全电容割集中的“独立”的部分．

4）两两求环和 令RN＝2．p＋q＝6≠RN程序往下执行．开始执行求环和．如：Set＝Acc1⊕Acc2＝｛C1，C2，C3｝，显然，Set＝Acc5，所以，可以认为Acc5是非独立的，应消除它，同时令Acc5＝｛0｝，K＝1，Acc1不再与Acc5求环和．在还没有消除Acc4之前，程序执行到Set＝Acc1⊕Acc4＝｛C1，I1，C3，C5，C7｝得到两个割集的并集，则不必管它，不执行消除判断．本例中，这一步还可消除Acc6＝Acc1⊕Acc3和Acc4＝Acc2⊕Acc3，所以K＝3．经过这一步，ACC中还剩下3个集合中的元素不为“0”，即（p＋q－K）＝1＋5－3＝3．

5）执行每3个集合求环和 RN＝RN＋1，RN＝p＋q－K＝3吗，若是，则程序结束．由于只剩下3个集合，所以不可能再消除某一个集合，所以程序不再往下执行．记录下Nindac＝p＋q－K＝3，而"独立"的全电容割集就是Acc1，Acc2和Acc3．

4 结 论

如果某电网络有NC个全电容割集，那么网络的系数矩阵A有NC个“0”特征根．图1中，利用分析软件易知，网络的复杂度为8，系数矩阵A的秩为5，且能控性矩阵的TC的秩为6，因此系统是不能控的，这意味着某个“0”根对应的状态变量是能控的．进一步分析3个全电容割集，可以知道，在Cut1中，电容C1的电压是能控的，这正是在分析系统结构性质时，需要找出这些“0”根的特殊结构，而研究这个算法的原因．

［1］Lu Kaisheng，Gao Guozhang．Various sufficient conditions of separability，reducibility，controllability and observability for electrical networks over F（z）［C］／／Proc．IEEE ICMLC，2007．

［2］Lu K S，Wei J N．Rational function matrices and structural controllability and observability［J］．IEE Proc－D，1991，138：388－394．

［3］Chen Shubai，Zuo Kai，Zhang Liangzhen．Network graph theory and its application ［M］．Beijing：Science Press，1982．

［4］Chen Waikai．Modern network analysis［M］．Beijing：People＇s Post ＆ Telecommunications Publishing House，1992．

［5］Guozhang Gao，Kaisheng Lu．Algorithms of analyzing RLC electrical network structure［J］．Proc．IEEE WCICA，2006，6：4 147－4 151．

［6］高国章，冯常奇，鲁凯生．域F（z）上RLC电网络结构性质分析的计算机实现［J］．武汉理工大学学报：交通科学与工程版，2006，30（1）：73－76．

［7］Zhang Ke，Gao Guozhang，Liu Guanmin，et al．A computer analysis program for finding state equation of RLC network over field of rational functions in muti－parameters［C］／／Proc IEEE Region 5 Technical Conference，2004：45－48．