软实时环境下机器人运动学逆解研究

李启源 裴海龙

(华南理工大学自动化科学与工程学院，广东 广州 510640)

0 引言

典型机器人控制系统一般采用分层递阶结构［1］，即将一个复杂的任务层分解落实，最终形成一系列底层硬件系统可高速串行执行的简单“原子级动作”。这样的控制系统适用于大型、复杂、多任务环境下的机器人系统，然而当考虑到空间安装尺寸、运算速度和价格等因素时，上述传统控制系统架构就有了其“力不从心”的地方。在这种情形下，开源软实时操作系统架构下的机器人控制系统应运而生。

1 机器人控制系统的组成

机器人控制系统采用基于PC的技术路线。硬件结构以PC104架构为基础，通过PCI/ISA总线连接以FPGA为核心的底层硬件电路;软件结构在RTLinux上进行二次开发，利用其实时性和多任务调度功能实现复杂的机器人任务［2］。

2 RTLinux及应用系统

RTLinux是在Linux内核下层添加了一个简单的实时内核［3］，将Linux本身作为这个实时内核的优先级最低的任务，即所有的实时任务的优先级都高于Linux系统本身的以及Linux系统下的一般任务［4］。RTLinux结构如图1所示。

图1 RTLinux结构图Fig.1 Structure of RTLinux

正常的Linux进程仍可以在Linux内核上运行，这样既可以使用标准分时操作系统即Linux的各种服务，又能提供低延时的实时环境［5］。

机器人控制系统的软件部分采用RTLinux平台，以C、C++语言编写，可以分为四部分:①人机接口(示教盒);②任务调度与分解进程，负责从用户界面进程获得指令输入，结合从运动规划与控制进程和传感器管理进程获得的当前系统状态，作出系统动作决策，并将当前允许执行的指令通过共享内存消息机制发送到下一层的进程执行;③运动规划与控制，根据任务调度与分解模块发出的运动指令，实现机器人正逆学分解及运动规划/插补计算、位置控制等;④传感器信息处理，接收外界信息后进行预处理，然后传递给任务调度与分解进程。这四部分各自以进程的形式独立运行，通过共享内存方式进行交互通信，其中运动规划与控制进程是实时进程，其他为常规进程。

按照功能划分，机器人控制系统结构如图2所示。

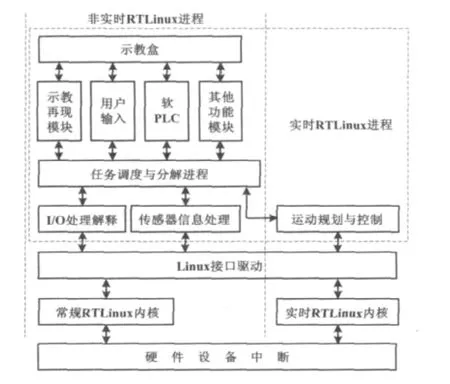
图2 机器人控制系统结构图Fig.2 Structure of robot control system

3 硬件接口设计

本文设计的机器人控制系统由上位机、运动控制接口电路和被控对象构成。上位机使用桑达的PC104，接口电路的核心部件是FPGA，被控对象为安川公司的交流伺服电机。机器人控制系统硬件电路结构如图3所示。

图3 硬件电路结构图Fig.3 Schematic of the hardware circuit

伺服电机自带光电编码器，能自动检测并反馈电机的位置值，反馈信号为相位差90°的A/B两相信号。A/B两相信号进入FPGA后，通过FPGA内部设计的计数器模块对A/B信号进行计数，获得各个电机的位置信息并存储在FPGA的内部寄存器中。PC104通过PCI/ISA总线，从FPGA中读取该寄存器的值，从而得到电机的位置值。将该电机的实际位置值与系统传输的理想位置值比较，得到一个偏差值，再根据一定的算法对偏差进行插补、PID运算等处理，得到一个新的控制信号。通过PCI/ISA总线，将控制信号发送给伺服控制板，最后通过FPGA中的pulse模块发送一定脉宽的脉冲，并通过伺服控制器驱动电机达到想要的速度和位置［6］。从上述原理来看，本设计构成对电机的双闭环控制，外部为位置环、内部为速度环，确保了电机运动的速度与精度。

4 机器人建模

现有机器人本体属于关节式机器人，其坐标系如图 4 所示［7］。

图4 机器人坐标系统Fig.4 Robot coordinate system

图4中，机器人的六个关节都是转动关节。前三个关节确定手腕参考点的位置，后三个关节确定手腕的方位。与大多数的工业机器人一样，最后三个关节轴交于一点。将该点选作手腕的参考点，同时选作为连杆坐标系{4}、{5}、{6}的原点。关节1的轴线为铅直方向，关节1和关节2的轴线垂直交错，距离为a1;关节2和关节3的轴线水平且平行，距离为a2;关节3和关节4的轴线垂直交错，距离为a3;关节3和关节4沿z轴方向的距离为d4。由图4可知，a1=150 mm、a2=570 mm、a3=150 mm、d4=650 mm。相应机器人的连杆参数如表1所示。

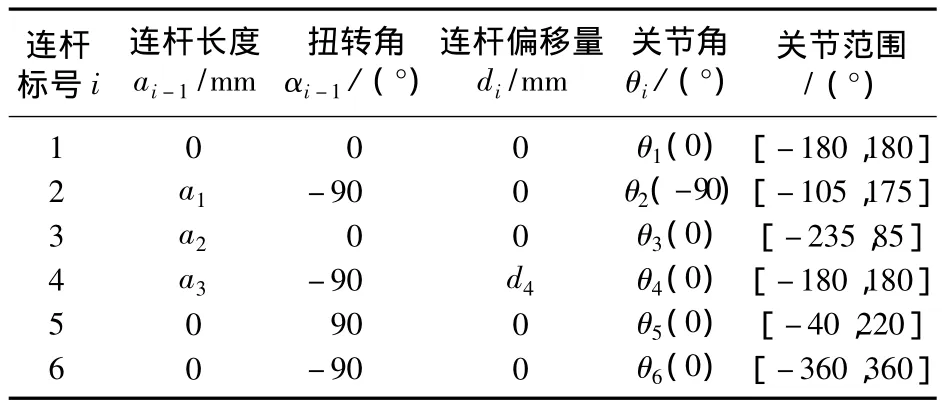
表1 机器人的连杆参数表Tab.1 Link parameters of robot

5 求解过程

基于现有机器人D-H模型，使用反变换法+Pieper方法讨论机器人的逆运动学问题，具体为利用Pieper方法求解 θ2、θ3，其他利用反变换法求解［8］。

在此已知的是世界坐标值 x、y、z、a、b、c，在求解过程中，首先要将世界坐标值转换为奇次变换矩阵。奇次变换矩阵包含平移和旋转两部分。平移部分即奇次变换矩阵的第四列的前三行的三个元素，它们是x、y、z的值;而旋转部分是前三行和前三列部分的九个元素，它们是 r、p、y(即 a、b、c)三个角度的正余弦组合。即:

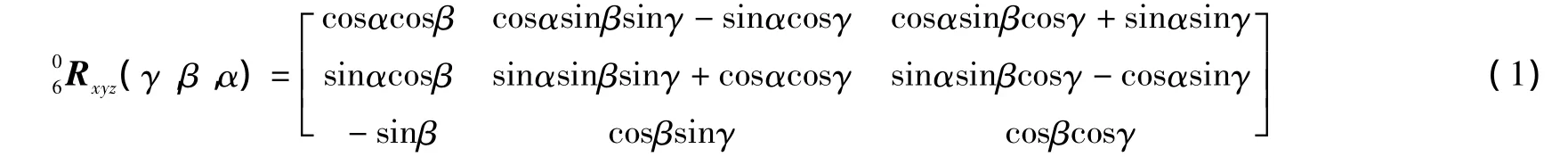
式中:γ=a、β=b、α=c。这样，由已知的世界坐标系中的a、b、c值就可以求得旋转矩阵06Rxyz(γ，β，α)。

θ1求解过程即利用反变换法求解θ1，由于上述模型中d2=0，故:

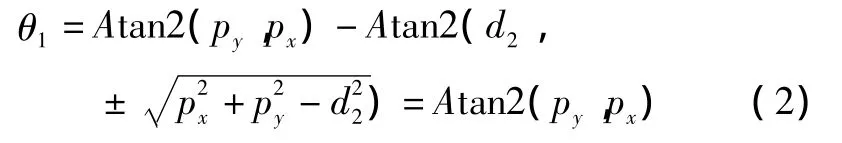
利用Pieper方法求解θ2和θ3，分别有:

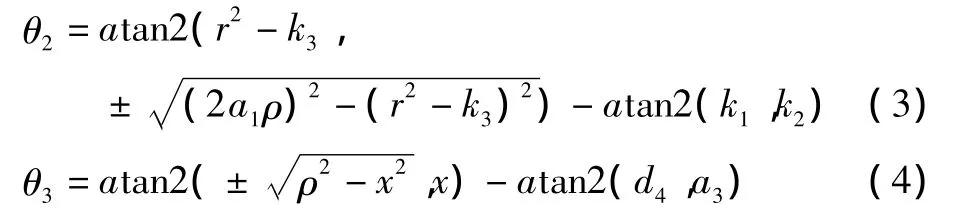
至此，可以求出 θ1、θ2、θ3的表达式，代入相应的参数即可求出其值。下面根据手腕方位来反解出θ4、θ5和θ6。在此选用反变换法，由于现有的机器人D-H模型与PUMA560的差别仅在于12T的第四列不同，即奇次变换矩阵12T中关于平移的部分不同，关于旋转的部分是完全一样的。

由于上文已经求出了θ1、θ2和θ3，则经推导可知:

只要 s5≠0，便可求出 θ4，即:

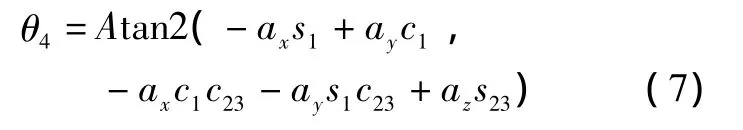
当s5=0时，操作臂处于奇异形位。此时，关节4与关节6重合，只能解出θ4与θ6的和或者差。奇异形位可以由式(7)中Atan2的两个变量是否都接近0来判断。若都接近0，则为奇异形位，否则不是奇异形位。在奇异形位时，可以任意选取θ4的值，再计算相应的θ6的值。根据求得的θ4，便可以进一步求解θ5，方法和求解θ4是一样的。θ5的封闭解为:

有了上述解，可求出θ6的封闭解为:

6 试验验证

通过上述软件实时系统和机器人坐标系统运动学系统的构建，即可形成真正的机器人控制系统。为验证机器人控制系统软件算法的正确性和可靠性，需要对工业机器人在伺服控制、运动控制板卡控制以及软件控制三种控制模式下的运动性能进行对比测试。对机器人各轴在同一控制模式下不同速度运行进行对比测试，可以揭示不同速度时的运动性能。

本方案采用激光测振仪对工业机器人各轴进行运动测试，给出各轴运动速度曲线和相关参数，从以上三个角度对机器人的运动性能进行对比分析。

测试仪器为Polytec激光测振仪和Tektronix四通道数字示波器。测试方案具体介绍如下。

①测试点布置:取点原则是尽量反映各轴的运动状态，以便于测量。机器人姿态为原点。

②测试方法:在三种控制模式下对各轴的运动性能对比测试。

③测试步骤:第一步是在机器人本体各测试点粘贴反光纸，调试仪器;第二步是在伺服控制模式下，将第一轴的运行速度分别设置为5 °/s、10 °/s、20 °/s，从初始位置单独进行小范围运动(－10°～+10°)，测量测试点的运动速度曲线和相应参数;第三步是在板卡控制模式下，将第一轴的运行速度分别设置为5°/s、10°/s、20 °/s，从初始位置单独进行小范围运动(－10°～+10°)，测量测试点的运动速度曲线及相应参数;第四步是在软件控制模式下，将第一轴的运行速度分别设置为 5 °/s、10 °/s、20 °/s，从初始位置单独进行小范围运动(－10°～+10°)，测量测试点的运动速度曲线和相应参数;第五步是使用第二步至第四步的方法，对2～6轴进行测试。

测试结果如图5所示，限于篇幅，只表现第六轴。与图5(a)和图5(c)相比，图5(b)是经过软件运动规划/伺服控制处理后系统第六轴以20°/s的速度运行得到的曲线，运行平滑稳定，毛刺较少。该结果充分说明了以RTLinux为核心的软实时控制系统在稳定性以及串联机构末端振动的抑制方面具有较好的效果。

7 结束语

本测试采用激光测振仪对工业机器人各轴进行小范围运动测试，得到各轴运动速度曲线和相关参数，并通过对比的方法，从三个角度对机器人的运动性能进行详细分析。通过对机器人1～6轴三种控制模式下的运动性能进行对比测试，结果表明，软件控制模式的效果优于伺服控制和板卡控制，排除了软件控制引起振动的可能;软件方式效果明显优于前两种，充分说明了基于RTLinux的机器人控制系统的有效性。

［1］国家863计划智能机器人专家组.机器人博览［M］.北京:中国科学技术出版社，2001.

［2］涂刚.嵌入式操作系统综述［J］.计算机应用研究，2000(11):4－6.

［3］周德新，张向利.Linux和嵌入式操作系统［J］.桂林电子工业学院学报:自然科学版，2000，20(4):21 －23.

［4］衷克定.大学信息技术(Linux操作系统及其应用)［M］.北京:清华大学出版社，2005.

［5］朱响斌，涂时亮.Linux的实时性能测试［J］.微电子学与计算机，2004，21(11):85 －88.

［6］刘韬，楼兴华.FPGA数字电子系统设计与开发实例导航［M］.北京:人民邮电出版社，2005.

［7］日本机器人学会.机器人技术手册［M］.宗光华，程君实，译.北京:科学出版社，2007.

［8］熊有伦.机器人技术基础［M］.武汉:华中科技大学出版社，1992.