小波包滤波在齿轮故障诊断中的应用

周翔 侯立刚 苏成利 肖炎良 张勇

(辽宁石油化工大学信息与控制工程学院，辽宁 抚顺 113001)

0 引言

齿轮是目前应用最为广泛的传动形式之一。齿轮在高强度的运作下会出现损伤，如断齿、磨损和剥落等。对齿轮故障进行研究，有助于提高设备的整体运行效率。

时频分析方法在齿轮故障诊断中比较常见，但诊断类型比较单一，针对性强［1］。多数据融合的方法是今后齿轮传动故障诊断的主要发展方向［2］。径向基函数(radial basis function，RBF)神经网络方法可进行齿轮故障诊断［3］。自适应小波神经网络(wavelet neural network，WNN)方法解决了用二进制尺度信号作为网络输入而故障特征信息可能恰好不在选用的二进制尺度上的问题［4］。小波包特征熵支持向量机故障诊断方法解决了建立故障类型识别模型难的问题［5］。但齿轮故障诊断还有许多要改进的地方，如时频分析方法对故障诊断的单一性和模糊性、网络训练的波动性、网络输入特征信号的准确性(信噪比低)等。

本文采用改进阈值函数的方法(一种小波包滤波方法)消除神经网络输入信号中的噪声，同时保留故障中所包含的特征信号，从而提高神经网络输入信号的信噪比。同时，对改进阈值函数的可行性进行了推导，结果表明改进后的系统能更加快速、准确地对多种齿轮故障进行判别。

1 小波包去噪

1.1 小波包分析

小波包分析的基本思想是把信号的高频和低频部分同时投影到由一组互相正交的小波函数构成的子空间上，使信号在不同尺度上展开，从而提取信号在不同频带上的特征，同时保留信号在各尺度上的时域特征。小波包分析是多分辨率分析的深化，有利于更好地提取特征信号。

尺度函数和小波函数的尺度关系如式(1)所示［6］:

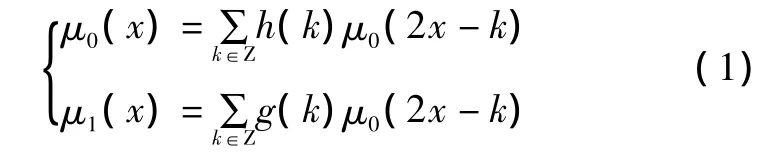
式中:μ0(x)为尺度函数;μ1(x)为小波函数;h(k)、g(k)为由小波函数确定的两列共轭滤波器系数。

μ2l(x)、μ2l+1(x)分别定义为:

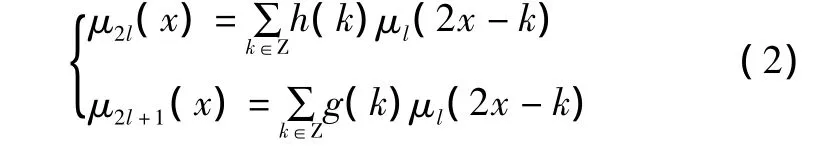
则 μn(x)(n=2l或 2l+1，l=0，1，…)即为关于正交尺度函数μ0(x)的小波包。

1.2 小波包分解与重构

将小波包与多分辨率相结合，再与归一化系数相乘，便可得到小波包分解公式，即:

最终信号在尺度j=J上进行分解的序列为{c2J－1，c2J－1+1，…，c2J}。

对二进制小波进行离散变换，可得:

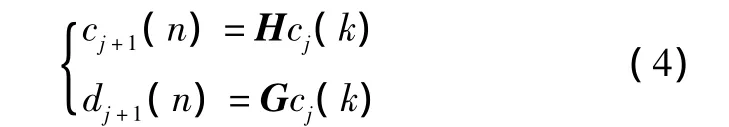
式中:H、G 为矩阵，H=(Hn，k)，G=(Gn，k)，其中，Hn，k=hk－2n，Gn，k=gk－2n。

信号的重构算法为:

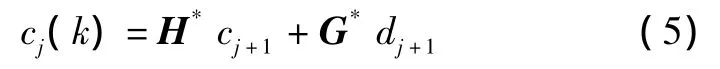
式中:矩阵H*、G*为H、G的对偶算子。通过分解后的序列，可以逐步恢复出原始信号。

1.3 小波包去噪原理和步骤

定义 设n为正整数，若存在常数A＞0和n次多项式Pn(x)，有:

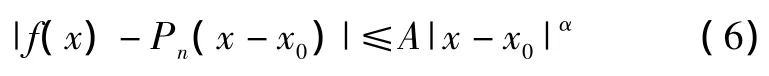
则称f(x)在点x0处为Lipα。如果在区间(a，b)上存在常数A，对任意 x(x0∈(a，b))，有 n次多项式Pn(x)满足式(6)，则称 f(x)在区间(a，b)上一致Lipα。在 x=x0处，当 α≠1，即 Lipα 不为 Lip1 时，f(x)在x0处是奇异的;若f(x)在x0处有界但不连续，则Lip的指数为0，其指数越大，f(x)越光滑。

对于噪声而言，小波变换在不同尺度下高度不相关，近似于处处奇异，其Lip指数为负，奇异性小于0。在小波变换下，噪声的平均幅值和尺度因子2j成反比关系，即噪声能量随尺度增大而减小。因此，通过改变小波尺度能够减小噪声。

小波包去噪的基本思想就是对小波包分解后的各层系数分别进行处理。通常有两种途径:一是已知所关心的频率成分，进行小波包分解时，保留所关心的频带的小波变换结果，将其他变换结果清0;二是已知噪声的频带范围，将小波变换后的噪声所在频带的小波包系数清0，然后再利用处理后的小波包系数重构出消噪后的信号。利用小波包进行消噪的基本步骤为:①利用小波包对输入信号进行分解;②确定最优的小波包基;③对小波包分解的系数进行阈值量化处理;④利用小波包分解系数和量化系数进行小波包重构。

1.4 改进阈值算法

本文选取一种新的阈值算法，克服了软阈值和硬阈值算法的缺陷，使其具有更强的弹性和适用性。阈值改进算法为［7］:

式中:α为阶次调节因子，α≥0，利用α可使构造的新函数的取值处于软、硬阈值函数之间;β为振荡调节因子，0≤β≤1，其影响信号的信噪比，该值越大，信号失真越严重，振荡越小。下面对改进阈值算法的连续性、可导性和收敛性进行分析。

1.4.1 连续性分析

设阈值函数为f(x)，则有:

当x=λ时，可得:

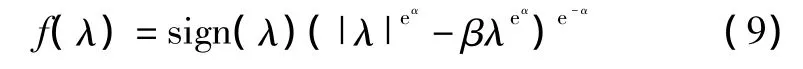
根据实际情况可知λ≥0，所以可以对式(9)继续进行化简，结果为:

此时选取β=1，可得:

所以，f(x)在x=λ处是连续的。

1.4.2 可导性分析

当x＞0时，sign(x)=1，因此f(x)可以化简为:

对x求偏导可得:

当x=0时，sign(x)=1，α取值为0，此时不能直接用求导公式求解，可利用导数定义求解，即:

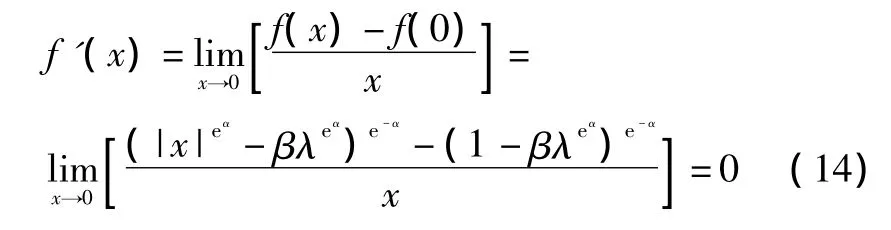
当 x＜0时，f'(x)=f(x)=0。

所以，f(x)是可导的。

1.4.3 收敛性分析

当x≥0时，有:

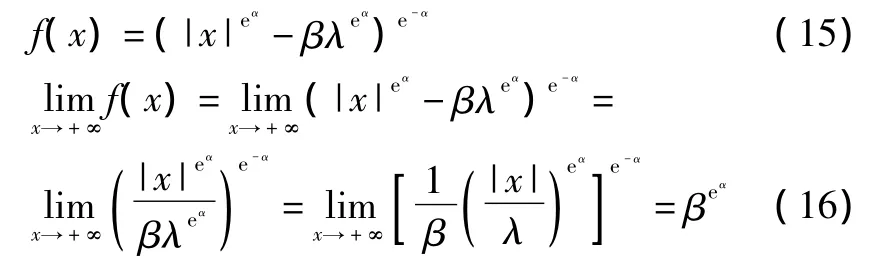
当x＜0时，f(x)=0，所以f(x)在无穷处是收敛的，且f(x)是连续函数。因此，f(x)在整个区间内是收敛的。

2 网络构造及其优化

本文采用三层紧致型小波神经网络［8］，小波基函数选取molet小波，输出函数选取sigmoid函数，即:

小波神经网络的输出为:

式中:xi为输入层第i个输入分量;yk为输出层的第k个输出分量;n、k、s分别为输入层、输出层和隐层的神经元个数;ωji为输入层第i个神经元到隐层的第j个神经元的连接权;ωkj为隐层第j个神经元到输出层第k个神经元的连接权。小波神经网络的目标函数为:

式中:tk为期望值。训练算法采用梯度下降法。本文在参数优化方面作了进一步改进，以对ωkj的优化为例，优化内容如下:

式中:β为遗忘因子;η为各个参数的学习速率;α(0＜α＜1)为各个参数的动量因子。其中，学习速率η取值如下:

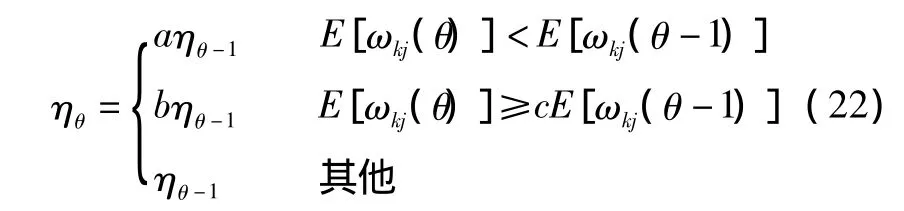
与以前的优化相比，改进后的参数优化法添加了遗忘因子β，它能使要优化的参数更加平稳，避免了优化后的参数出现太大波动。

3 仿真

仿真中用到的数据集是通过试验获得的。试验中，在轴承底座安装加速度传感器，滚动轴承带动齿轮运转，产生振动信号。滚动轴承的转速为1500 r/min。

本文选取db4小波，分解层数为3，并依据最小shannon熵准则选取最优小波包基;设置阈值时，取α=2.9、β=0.8。

小波包去噪前后的仿真结果如图1所示。由图1可以看出，含噪信号中的噪声部分已经被很好地去除，信号特征保持完整。

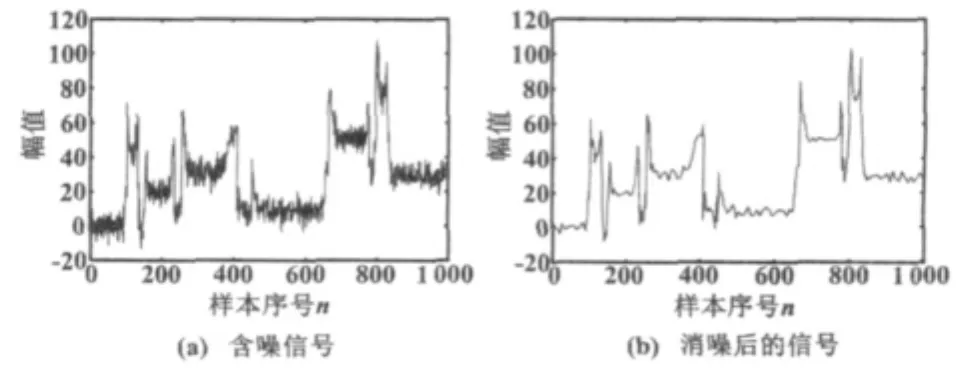
图1 小波包去噪前后的仿真结果Fig.1 Simulation results of before and after wavelet packet de-nosing

网络的训练样本从试验数据中选取，共选取15组样本，分成3种模式，其中每种模式的最后一组样本(共3组)用来进行检验。然后对数据作进一步处理，即提取信号特征向量并对其进行规范化处理，将其变化到［0，1］的范围，小波包特征向量归一化处理公式为:

式中:P和Pn分别为归一化前后小波包特征向量;小波神经网络中的小波基函数为molet小波函数;Pnmean和Pstd分别为molet小波特征向量P的均值和方差。

齿轮的振动特征参数选择为［9－10］:峰值因子、峭度指标、脉冲指标、裕度指标、一-二阶啮合频率比、一-二阶旋转频率比、一-三阶啮合频率比和一-三阶旋转频率比共8个参数。齿轮故障诊断明细如表1、表2所示。

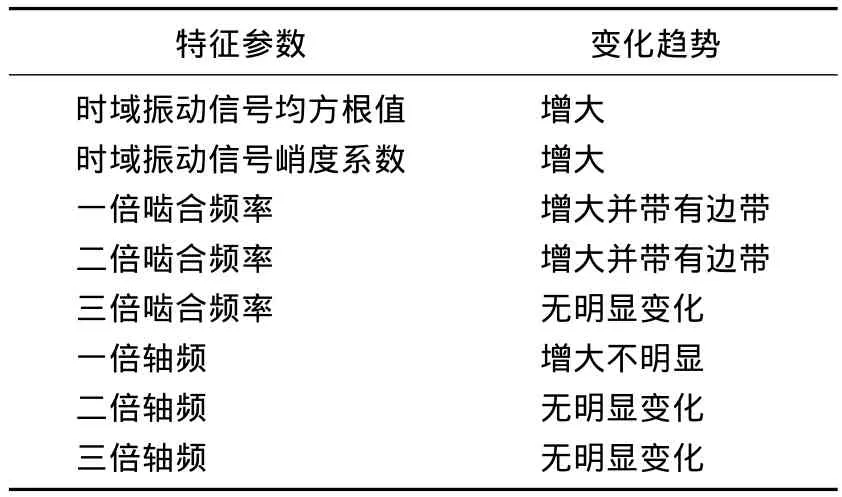
表1 齿轮断齿明细表Tab.1 The details of broken teeth for gears

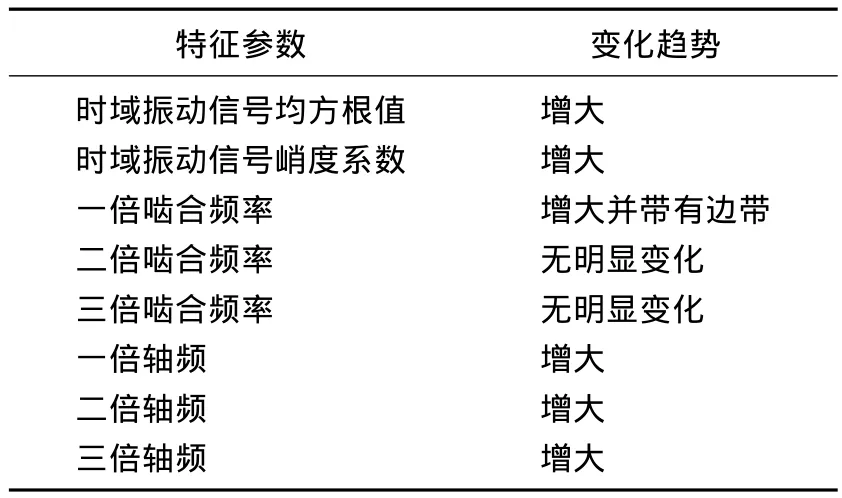
表2 齿轮偏心明细表Tab.2 The details of eccentric gears

小波神经网络的隐层节点数选取为36，优化中的遗忘因子β选取为0.6，学习速率η为0.835，目标误差设为0.01。信号经去噪后的改进小波神经网络故障诊断的误差曲线如图2所示。

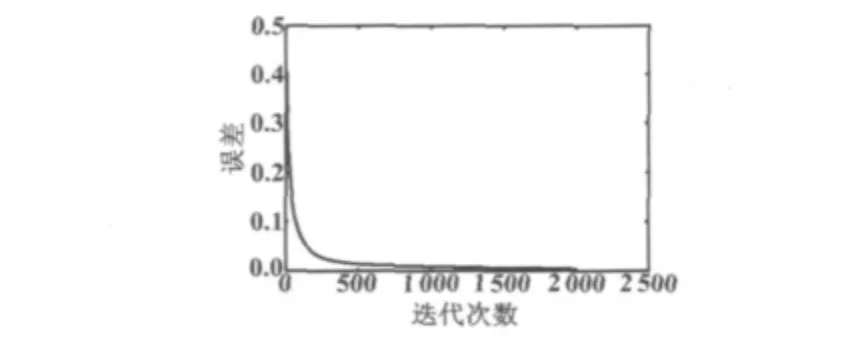
图2 信号去噪后的改进WNN误差曲线Fig.2 The error curve of improved WNN after signal de-noising

为了表明经过信号去噪后的改进型小波神经网络能更快更准确地确定齿轮故障，对去噪后的BP神经网络和去噪前的改进小波神经网络进行了对比，误差曲线如图3和图4所示。

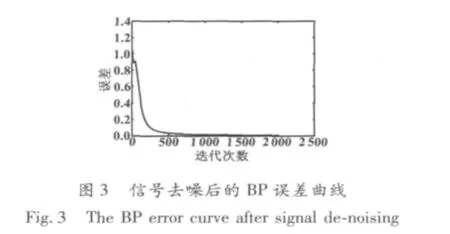
由图2和图3可以看出:信号经过去噪后的改进小波神经网络大约只要470步就能使目标达到要求;BP神经网络大约需要1500步才能达到目标要求，训练的起始误差较大且有一定程度的起始波动。即图2和图3对比说明了信号去噪后经过小波神经网络比经BP神经网络训练速度更快、更稳定。而信号未处理的改进小波神经网络则大约需要800步才能达到目标要求，达到要求后继续训练则会出现波动，即图2和图4的比较说明信号通过滤波处理后的小波神经网络运算更快更准确且不会产生波动。因此，可以得出，信号去噪后作为网络输入数据的改进小波神经网络能快速且稳定地判断齿轮故障。检验样本的期望输出和实际输出如表3、表4所示。

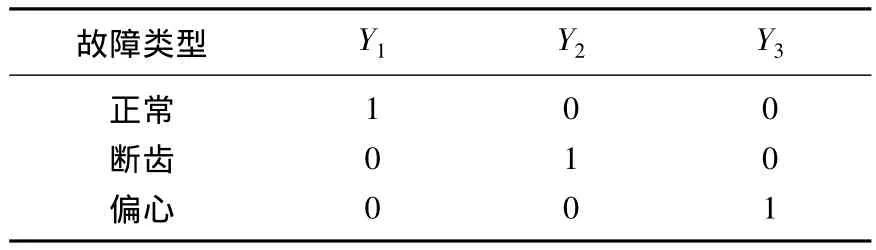
表3 检验样本的期望输出Tab.3 The expected output of inspection samples

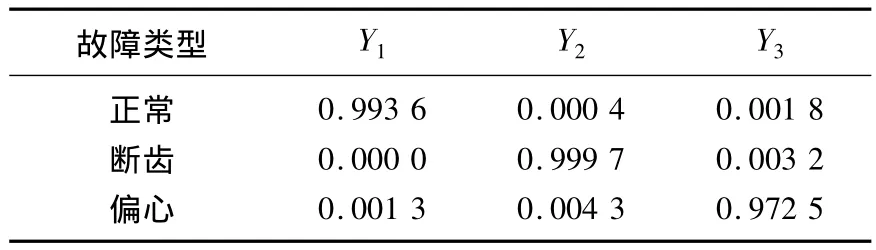
表4 检验样本的实际输出Tab.4 The actual output of inspection samples

表3和表4的输出结果显示，实际输出与期望值大致吻合，完全在误差范围之内，进一步证明了该方法的可行性和有效性。

4 结束语

采用小波包分析方法对齿轮的振动信号进行消噪预处理，有效地消除了信号当中的干扰成分，提高了信噪比。改进小波神经网络在齿轮故障诊断中起着故障分类的作用，且改进小波神经网络的训练过程比较稳定，训练速度也更快。通过仿真发现，该方法用于齿轮故障诊断是有效可行的，诊断准确率较高，满足对齿轮故障诊断的技术要求。

［1］安婧，伉大俪，郭海涛，等.时-频分析方法在齿轮故障诊断中的应用［J］.信息技术，2010，23(3):103 －108.

［2］王建平，肖刚.齿轮传动故障诊断方法综述及应用研究［J］.江苏船舶，2008，25(1):24 －26，41.

［3］鲍泽富，徐李甲，王江萍.基于小波包变换与神经网络的齿轮故障诊断方法［J］.机械研究与应用，2010(1):21－25.

［4］陈文戈，赵学智.轴承故障的自适应小波神经网络分类［J］.轴承，2009(3):37 －40.

［5］崔厚玺，张来斌，王朝晖，等.基于小波包特征熵SVM的压缩机气阀故障诊断研究［J］.石油化工高等学校学报，2009，22(1):86 －88.

［6］虞和济，陈长征，张省，等.基于神经网络的智能诊断［M］.北京:冶金工业出版社，2000.

［7］程文波，王华军.基于改进阈值的小波包图像去噪方法研究［J］.湖南科技大学学报:自然科学版，2009，24(1):77－81.

［8］芮执元，徐龙云，冯瑞成，等.基于小波神经网络的齿轮故障诊断［J］.机械传动，2008(1):80－84.

［9］徐龙云，芮执元.基于小波神经网络的齿轮故障诊断［D］.兰州:兰州理工大学，2007.

［10］黄志刚，林凤涛.小波神经网络在齿轮故障诊断中的应用［J］.制造技术与机床，2009(4):55－57.