碱金属化物M+aza222Mʹ-(M,Mʹ=Li,Na,K)的结构及非线性光学性质
樊丽涛 李 莹 吴 迪 李志儒 孙家钟
(吉林大学理论化学研究所,理论化学计算国家重点实验室,长春130023)
碱金属化物M+aza222Mʹ-(M,Mʹ=Li,Na,K)的结构及非线性光学性质
樊丽涛 李 莹 吴 迪*李志儒 孙家钟
(吉林大学理论化学研究所,理论化学计算国家重点实验室,长春130023)
采用密度泛函理论(DFT)B3LYP方法得到具有有机穴状配体的碱金属化物M+aza222Mʹ-(M,Mʹ=Li, Na,K)的几何结构.并使用了BHandHLYP方法计算了此体系的非线性光学(NLO)性质.结果表明:该体系具有很大的一阶超极化率(β0),对于Li+aza222K-体系,β0值达到1.0×106a.u.;体系的β0值及配体aza222内外的碱金属之间距离与碱金属的原子序数均存在着依赖关系.通过与其它碱金属化物的β0值对比发现,aza222配体能够显著增大碱金属化物的一阶超极化率.
密度泛函理论;非线性光学; 碱金属化物; 一阶超极化率; 穴状配体
1 引言
近几十年来,非线性光学材料因其在光通信、光信息存储、光计算及全光开关等高科技领域的潜在应用而引起广泛的重视,设计优良的非线性光学材料一直是理论和实验研究的热门课题.1-7文献8-12报道了带有额外电子的体系会有很大的非线性光学响应,其中有代表性的一类体系是碱金属化物(alkalide).
1974年,碱金属化物作为一种特殊的晶体盐被成功地合成和表征.13,14碱金属化物的特殊性在于体系中阴离子的部分是带负电荷的碱金属原子(例如, Li-,Na-,K-),与之构成电荷平衡的阳离子部分则是比较复杂的有机碱金属复合物.最近的理论研究已预测含有杯状配体calix[4]pyrrole,15笼状配体adamanzane(Adz)的碱金属化物表现出很大的一阶超极化率值.16,171999年,Dye研究小组18合成了一类室温下稳定的具有穴状配体(CH3)6Azacryptand[2.2.2] (简写为aza222)的碱金属化物,即为K+(aza222)Na-和K+(aza222)K-.本文基于此体系的实验背景,系统研究了碱金属化物M+aza222Mʹ-(M,Mʹ=Li,Na,K)的结构和非线性光学性质.根据密度泛函方法计算讨论了体系的几何结构和一阶超极化率与碱金属原子序数之间的依赖关系,并讨论了配体的改变对碱金属化物的非线性光学响应的影响,为高性能非线性光学材料的设计提供了理论依据.
2 计算方法
M+aza222Mʹ-(M,Mʹ=Li,Na,K)体系的几何构型是在B3LYP/6-31G方法下优化得到的.对于大有机体系的一阶超极化率,B3LYP方法会产生过高的估算结果,19MP2方法计算结果比较准确,但需要消耗大量的计算资源.已有文献20,21指出BHandHLYP方法可以在很大程度上降低B3LYP对体系一阶超极化率的高估结果.在以前的工作中17我们也通过对比B3LYP,MP2,BHandHLYP方法对于笼状配体碱金属化物(M+@n6Adz)Mʹ-体系一阶超极化率的计算结果,发现B3LYP方法过高估计了体系的一阶超极化率值,而BHandHLYP结果更接近较高水平的MP2的计算结果.因此我们认为BHandHLYP方法可以更有效地描述有机碱金属化物体系的非线性光学性质.本文采用BHandHLYP方法计算了分子的平均偶极矩,平均极化率和平均一阶超极化率.所有计算中对配体aza222上的C、H、N原子使用6-311++G基组,对碱金属(M,Mʹ)原子使用6-311+ G(3df)基组.
分子在弱的外加电场的作用下其能量可以表示为:

式中E0是无外加电场时分子的能量,Fα是外电场在α方向上的分量,μα、ααβ和βαβγ分别是偶极矩、极化率和一阶超极化率张量的一个分量.平均偶极矩、平均极化率和平均一阶超极化率分别定义为:

该体系的自然键轨道(NBO)22电荷和垂直电离能(VIE)使用B3LYP方法得到,计算中对C、H、N原子使用了6-311++G基组,对碱金属原子使用了6-311+G(3df)基组.
本文的全部计算均使用Gaussian 09程序包23完成,最高占据分子轨道(HOMO)图由GaussView程序24生成.
3 结果与讨论
3.1 几何结构
图1为M+aza222Mʹ-(M,Mʹ=Li,Na,K)体系的几何构型示意图.表1中列出了该体系的相关参数.
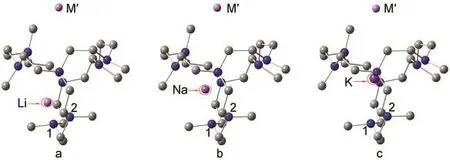
图1 碱金属化物M+aza222Mʹ-的优化几何结构Fig.1 Optimized structures of the M+aza222Mʹ-alkalidesH atoms are not displayed;M represents(a)Li,(b)Na,(c)K.

表1 M-Mʹ,M-N1,M-N2和Mʹ-H的距离、碱金属原子上自然键轨道(NBO)电荷以及碱金属化物的垂直电离能(VIE)Table 1 M-Mʹ,M-N1,M-N2,and Mʹ-H distances,natural bond orbital(NBO)charges on alkali atoms,and vertical ionization energies(VIE)of the alkalides
在之前报道的以笼状Adz为配体的碱金属化物中,配体内部的碱金属原子处于Adz笼的中心附近.16然而在M+aza222Mʹ-体系中,配体内部的碱金属并不都位于穴的中心位置.对比图1中a、b、c三个结构,可以看出当配体内碱金属原子从K→Na→Li依次变化时,中心碱金属原子(M)逐渐靠近穴的底侧.表1中的d(M-N1),d(M-N2)值代表中心碱金属原子(M)与配体底部两个氮原子(N1,N2)之间的距离.如表1所示,碱金属M按K→Na→Li顺序改变时,体系的d(M-N1)和d(M-N2)分别按照0.299-0.296 nm(M=K)→0.282-0.279 nm(M=Na)→0.218 nm(M=Li)和0.308-0.304 nm(M=K)→0.290-0.279 nm(M=Na)→0.223-0.222 nm(M=Li)顺序递减.这进一步证明了aza222内部的碱金属原子随原子序数的减小而逐步偏向穴的一侧.这种偏移有利于半径较小的碱金属原子与aza222配体上的叔胺氮原子相互作用,通过氮原子上的孤对电子对碱金属阳离子的配位而更有利于碱金属化物的稳定.

图2 d(M-Mʹ)与碱金属Mʹ原子序数的依赖关系Fig.2 Relationship between the d(M-Mʹ)and alkali Mʹatomic number
图2给出了配体内外碱金属之间的距离d(M-Mʹ)与碱金属的原子序数之间的依赖关系.如图2所示,当配体内部碱金属M固定不变时,随着配体外部碱金属Mʹ原子序数的增大,d(M-Mʹ)呈单调递增的规律.当M=Li时,d(M-Mʹ)的次序是0.640 nm(Li-Li)<0.659 nm(Li-Na)<0.712 nm(Li-K).同样,当M为Na和K时,d(M-Mʹ)次序分别是,0.632 nm(Na-Li)<0.653 nm(Na-Na)<0.709 nm(Na-K)与0.571 nm(K-Li)<0.595 nm(K-Na)<0.661 nm (K-K).同时,穴状配体外部碱金属原子Mʹ与最近的H原子之间的距离d(Mʹ-H)也具有同样的变化规律,随着配体外部Mʹ原子序数的增大,Mʹ-H的距离单调递增,Mʹ逐渐远离配体.相反,当配体外部碱金属Mʹ固定不变时,随着配体内碱金属M原子序数的递增,d(M-Mʹ)呈单调递减变化.如表1所示,当配体外碱金属Mʹ分别为Li、Na、K时,d(M-Mʹ)的变化顺序分别为,0.640 nm(Li-Li)>0.632 nm(Na-Li)>0.571 nm(K-Li),0.659 nm(Li-Na)>0.653 nm (Na-Na)>0.595 nm(K-Na),0.712 nm(Li-K)>0.709 nm(Na-K)>0.661 nm(K-K).这是由于配体内部碱金属原子随原子序数的增加而从穴的底侧逐渐向穴的中心靠近,这种位置的变化使配体内外碱金属原子间的距离逐步减小.
3.2 自然键轨道电荷和垂直电离能
图3为M+aza222Mʹ-体系HOMO图.如图所示,这个体系具有弥散的电子云.这是由于aza222配体上叔胺氮的孤对电子都是指向配体内部的,对穴内碱金属M的电子有很强的排斥作用,这种作用导致M的最外层电子离开M,转移到配体外并围绕在穴外的碱金属Mʹ周围.由于碱金属原子的电子亲和势很小,所以无法紧紧束缚住来自于配体内碱金属的电子,而使这个电子在其附近呈现弥散状态.

图3 M+aza222Mʹ-(M,Mʹ=Li,Na,K)的最高占据分子轨道图Fig.3 HOMOs of M+aza222Mʹ-(M,Mʹ=Li,Na,K)HOMO:the highest occupied molecular orbital
M+aza222Mʹ-体系的NBO电荷和VIE值列于表1中,从表1中可知,配体外部碱金属原子Mʹ的NBO电荷在-0.736e--0.842e之间,说明Mʹ以阴离子的形式存在,而M+aza222Mʹ-体系具有典型的碱金属化物的特征.值得注意的是Mʹ-上的NBO电荷要远远大于杯状配体的碱金属化物Li+(calix[4]pyrrole) Mʹ-中Mʹ-的NBO电荷(-0.253e--0.361e).15这是由于在Li+(calix[4]pyrrole)Mʹ-体系中,Mʹ与最近的H原子间的距离大约是0.30 nm,而在M+aza222Mʹ-体系中这个距离较长,在0.34 nm左右,因此Li+(calix [4]pyrrole)Mʹ-体系中Mʹ原子上负电荷较少的原因是Mʹ与附近H原子共享电子的结果.
如表1所示M+aza222Mʹ-体系具有较小的VIE值(2.519-2.864 eV),说明了这种碱金属化物中的额外电子是弥散的.同时VIE值显示出非常好的规律性:当配体内部碱金属(M)固定不变时,随着外部碱金属(Mʹ)原子序数的递增,VIE值单调递减;反之,当配体外部碱金属(Mʹ)固定不变时,随着穴内碱金属(M)原子序数的递增,VIE值单调递增.例如,当M=Li时,VIE值变化规律为2.729 eV(Mʹ=Li)>2.719 eV(Mʹ=Na)>2.519 eV(Mʹ=K);当Mʹ=Li时, VIE值变化规律为2.729 eV(M=Li)<2.780 eV(M= Na)<2.864 eV(M=K).这是由于当穴内碱金属原子(M)固定时,M与N1和N2的距离几乎不受Mʹ变化的影响,体系的垂直电离能主要由配体外碱金属原子(Mʹ)对电子的束缚能力决定,随着Mʹ由Li→Na→K变化,Mʹ的电子亲和势逐渐减小,对额外电子的束缚能力逐渐减弱,因此体系的垂直电离能依次减小;当配体外的碱金属原子(Mʹ)固定而配体内部碱金属原子(M)序数按Li→Na→K顺序增大时,M与N1、N2的距离显著增大,配体上的氮对M的推电子作用迅速减小,导致配体外碱金属Mʹ上的负电荷逐渐减少,而整个体系对电子的束缚能力相对变大,从而体系的垂直电离能逐渐增大.
3.3 非线性光学(NLO)性质
使用BHandHLYP方法计算了M+aza222Mʹ-体系的非线性光学性质(见表2).计算结果表明碱金属化物M+aza222Mʹ-具有较大的极化率(α0=732-1357 a.u.)和非常大的一阶超极化率(β0=16670-1003529 a.u.).其中Li+aza222K-的一阶超极化率β0≈1.0×106a.u.,是已知具有杯状配体的碱金属化物Li+(calix[4] pyrrole)K-的一阶超极化率(β0=3.6×104a.u.)的28倍,分别是具有笼状配体的碱金属化物(Li+@26Adz)K-(β0=1.6×105a.u.)和(Li+@36Adz)K-(β0=2.0×105a.u.)的一阶超极化率的6倍和5倍.以上数据说明,在增强碱金属化物的非线性光学响应上,穴状配体aza222不仅远优于杯状配体calix[4]pyrrole,而且优于笼状配体26adamanzane和36adamanzane.证明了有机配体的选择对设计具有高效的非线性光学响应的碱金属化物有着重要的作用.
图4给出了M+aza222Mʹ-体系的一阶超极化率与碱金属原子序数的依赖关系.通过与之前报道过的具有杯状或笼状配体的碱金属化物对比,我们发现具有穴状配体的M+aza222Mʹ-体系同样表现出了一阶超极化率对碱金属Mʹ序数存在依赖性.由图4可见,当固定穴内碱金属原子M时,体系的一阶超极化率β0随着穴外碱金属Mʹ原子序数的增加而增大.如表2所示,当内部碱金属原子M依次为Li、Na、K时,β0的变化规律分别为61864 a.u.(Mʹ=Li)<111340 a.u.(Mʹ=Na)<1003529 a.u.(Mʹ=K),30693 a.u.(Mʹ=Li)<119071 a.u.(Mʹ=Na)<587516 a.u.(Mʹ= K),16670 a.u.(Mʹ=Li)<19262 a.u.(Mʹ=Na)<169036 a.u.(Mʹ=K).

表2 碱金属化物的平均一阶超极化率(β0),平均极化率(α0),平均偶极矩(µ0),跃迁能(ΔE),振子强度(f0)以及最主要的跃迁轨道Table 2 Mean first hyperpolarizabilities(β0),polarizabilities(α0),dipole moments(µ0),transition energies(ΔE), oscillator strength(f0),and the main transition orbitals of crucial excited state of alkalides

图4 一阶超极化率对碱金属Mʹ原子序数的依赖关系Fig.4 Relationship between the first hyperpolarizability and the alkali Mʹatomic number
根据双能级公式可以分析M+aza222Mʹ-体系具有较大的一阶超极化率(β0)的原因,在静态条件下(扰动频率ω=0.0),双能级公式可表示为:25

上式中,ΔE、f0和Δμ分别代表体系最主要激发态的跃迁能、振子强度和基态与最主要激发态之间的偶极矩差.其中β0的值与ΔE3成反比,可见ΔE是影响体系一阶超极化率的最主要因素.本文使用含时Hartree-Fock方法得到了M+aza222Mʹ-体系的最主要激发态的跃迁能和振子强度以及主要的跃迁轨道(见表2).由于M+aza222Mʹ-体系的电子云弥散特性使其基态电子很容易被激发,因此这个体系的最主要激发能很小,仅为1.220-1.574 eV,这是体系具有大的一阶超极化率的本质原因.同时,配体外碱金属Mʹ的原子序数越大,碱金属的电子亲和势越小,其对额外电子的束缚能力越弱,额外电子云的弥散程度越高,因此碱金属Mʹ的原子序数的增加伴随着体系激发能的减小,而小的激发能可以带给体系更大的一阶超极化率,这是碱金属化物的一阶超极化率具有碱金属Mʹ序数依赖性的原因所在.由表2可知,当固定穴内的碱金属M不变时,体系的激发能ΔE随着穴外碱金属Mʹ的原子序数的增大而明显减小,因此,体系的β0值的变化规律为: M+aza222Li-<M+aza222Na-<M+aza222K-.
4 结论
本文使用B3LYP方法优化了M+aza222Mʹ-(M, Mʹ=Li,Na,K)体系的几何结构,并使用BHandHLYP方法计算了该体系的非线性光学性质.NBO结果表明,体系中aza222配体外部的碱金属原子Mʹ以阴离子形式存在,是典型的碱金属化物.分析该碱金属化物的结构和性质可知:(1)配体内外碱金属之间的距离d(M-Mʹ)依赖于碱金属原子序数呈规律性变化;若固定穴内碱金属原子M,d(M-Mʹ)距离随穴外碱金属Mʹ原子序数增大而增大,若固定穴外碱金属原子Mʹ,d(M-Mʹ)距离随穴内碱金属M原子序数增大而减小.(2)由于碱金属阴离子的电子弥散特性,体系的VIE值较小,对碱金属的原子序数依赖性与d(M-Mʹ)完全相反.当穴内碱金属原子M不变时, VIE值随穴外碱金属Mʹ原子序数增大而减小;当穴外碱金属原子Mʹ不变时,VIE值随穴内碱金属M原子序数的增大而增大.(3)M+aza222Mʹ-具有很大的一阶超极化率,β0值高达1.67×104-1.00×106a.u.,并且一阶超极化率与碱金属Mʹ的原子序数之间存在着单调依赖关系,当穴内碱金属原子M固定,随外部碱金属Mʹ原子序数的增大,一阶超极化率单调递增.与其它不同配体的碱金属化物相比,穴状aza222配体在增强体系一阶超极化率方面显示出良好的优越性.
(1) Eaton,D.F.Science 1991,253,281.
(2) Geskin,V.M.;Lambert,C.;Brédas,J.L.J.Am.Chem.Soc. 2003,125,15651.
(3) Nakano,M.;Fujita,H.;Takahata,M.;Yamaguch,K.J.Am. Chem.Soc.2002,124,9648.
(4) Kirtman,B.;Champagne,B.;Bishop,D.M.J.Am.Chem.Soc. 2000,122,8007.
(5)Avramopoulos,A.;Reis,H.L.J.;Papadopoulos,M.G.J.Am. Chem.Soc.2004,126,6179.
(6) Qiu,Y.Q.;Liu,C.G.;Chen,H.;Su,Z.M.;Yang,G.C.;Wang, R.S.Acta Phys.-Chim.Sin.2006,22,836.[仇永清,刘春光,陈 徽,苏忠民,杨国春,王荣顺.物理化学学报,2006,22, 836.]
(7) Sun,X.X.;Liu,Y.;Zhao,H.B.;Sun,S.L.;Liu,C.G.;Qiu,Y. Q.Acta Phys.-Chim.Sin.2011,27,315.[孙秀欣,刘 艳,赵海波,孙世玲,刘春光,仇永清.物理化学学报,2011,27,315.]
(8) Li,Y.;Li,Z.R.;Wu,D.;Li,R.Y.;Hao,X.Y.;Sun,C.C. J.Phys.Chem.B 2004,108,3145.
(9) Chen,W.;Li,Z.R.;Wu,D.;Li,Y.;Sun,C.C.;Gu,F.L.J.Am. Chem.Soc.2005,127,10977.
(10) Xu,H.L.;Li,Z.R.;Wu,D.;Wang,B.Q.;Li,Y.;Gu,F.L.; Aoki,Y.J.Am.Chem.Soc.2007,129,2967.
(11) Chen,W.;Li,Z.R.;Wu,D.;Gu,F.L.;Hao,X.Y.;Wang,B.Q.; Li,R.J.;Sun,C.C.J.Chem.Phys.2004,121,10489.
(12) Jing,Y.Q.;Li,Z.R.;Wu,D.;Li,Y.;Wang,B.Q.;Gu,F.L. J.Phys.Chem.B 2006,110,11725.
(13) Dye,J.L.;Ceraso,J.M.;Lok,M.T.;Barnett,B.L.;Tehan,F.J. J.Am.Chem.Soc.1974,96,608.
(14) Tehan,F.J.;Barnett,B.L.;Dye,J.L.J.Am.Chem.Soc.1974, 96,7203.
(15) Chen,W.;Li,Z.R.;Wu,D.;Li,Y.;Sun,C.C.;Gu,F.L.;Aoki, Y.J.Am.Chem.Soc.2006,128,1072.
(16) Chen,W.;Li,Z.R.;Wu,D.;Li,Y.;Li,R.Y.;Sun,C.C.J.Phys. Chem.A 2005,109,2920.
(17) Wang,F.F.;Li,Z.R.;Wu,D.;Wang,B.Q.;Li,Y.;Li,Z.J.; Chen,W.;Yu,G.T.;Gu,F.L.;Aoki,Y.J.Phys.Chem.B 2008, 112,1090.
(18) Kim,J.;Ichimura,A.S.;Huang,R.H.;Redko,M.;Phillips,R. C.;Jackson,J.E.;Dye,J.L.J.Am.Chem.Soc.1999,121, 10666.
(19) Champagne,B.;Perpete,E.A.;Jacquenmin,D.;van Gisbergen, A.S.J.;Baerends,E.J.;Soubra-Ghaoui,C.;Robins,K.A. J.Phys.Chem.A 2000,104,4755.
(20) Champagne,B.;Botek,E.;Nakano,M.;Nitta,T.;Yamaguchi, K.J.Chem.Phys.2005,122,114315.
(21) Nakano,M.;Kishi,R.;Nitta,T.;Kubo,T.;Nakasuji,K.; Kamada,K.;Ohta,K.;Champagne,B.;Botek,E.;Yamaguchi, K.J.Phys.Chem.A 2005,109,885.
(22) Reed,A.E.;Weinstock,R.B.;Weinhold,F.J.Chem.Phys. 1985,83,735.
(23) Frisch,M.J.;Trucks,G.W.;Schlegel,H.B.;et al.Gaussian 09, RevisionA.01;Gaussian Inc.:Wallingford,CT,2009.
(24) Dennington,R.T.K.;Millam,J.;Eppinnett,K.;Hovell,W.L.; Gilliland,R.GaussView,Version 3.09;Semichem,Inc.: Shawnee Mission,KS,2003.
(25) Oudar,J.L.;Chemla,D.S.J.Chem.Phys.2005,66,2664.
October 12,2011;Revised:December 11,2011;Published on Web:December 21,2011.
Structures and Nonlinear Optical Properties of the Alkalides M+aza222Mʹ-(M,Mʹ=Li,Na,K)
FAN Li-Tao LI Ying WU Di*LI Zhi-Ru SUN Chia-Chung
(State Key Laboratory of Theoretical and Computational Chemistry,Institute of Theoretical Chemistry, Jilin University,Changchun 130023,P.R.China)
Using density functional theory with the B3LYP functional,the optimized structures of the organic alkalides M+aza222Mʹ-(M,Mʹ=Li,Na,K,and aza222=Azacryptand[2.2.2])were calculated.The nonlinear optical(NLO)properties of these species were calculated by the BHandHLYP method.The results indicate that the M+aza222Mʹ-alkalides exhibit very large first hyperpolarizabilities(β0)up to 1.0×106a.u.(for M=Li,Mʹ=K).Both the first hyperpolarizabilities and the M-Mʹdistances of M+aza222Mʹ-were found to depend on the atomic number of the alkali metal atom M(Mʹ).By comparing the β0values of various organic alkalides,aza222 was found to be preferable to the previously investigated complexants in enhancing the first hyperpolarizabilities of alkalides.
Density functional theory;Nonlinear optics;Alkalide;First hyperpolarizability; Cryptand complexant
10.3866/PKU.WHXB201112212
O641
∗Corresponding author.Email:wud@mail.jlu.edu.cn;Tel:+86-431-81707218.
The project was supported by the National Natural Science Foundation of China(21043003,21173095).
国家自然科学基金(21043003,21173095)资助项目

