O/N替代掺杂对zigzag型硼氮窄纳米带能带及输运特性的影响
陈余行 张朝民 吴建宝 林 琦
(上海工程技术大学基础教学学院,上海201620)
O/N替代掺杂对zigzag型硼氮窄纳米带能带及输运特性的影响
陈余行 张朝民 吴建宝*林 琦
(上海工程技术大学基础教学学院,上海201620)
用第一性原理非平衡格林函数方法研究了O原子掺杂zigzag型硼氮窄纳米带(z-BNNNRs)的能带结构和电子输运特性.研究结果表明:O原子对N原子的替代掺杂使z-BNNNRs的能带结构出现明显变化,体系由半导体转变为金属;O掺杂明显地改变了z-BNNNRs体系的导电性能,在一定的偏压范围内产生明显的负微分电阻(NDR)现象,边缘掺杂比中间掺杂产生更大的负微分电导,进一步的输运性质计算给出的透射谱也印证了这一点.随着掺杂浓度的增加,负微分电导的极值也随之增大.
硼氮纳米带;氧掺杂;能带结构;输运性质;负微分电阻
1 引言
2004年英国曼彻斯特大学科学家通过机械剥离的方法首次成功地获得了二维平面结构的石墨片,1开创了低维纳米体系研究的新天地.2005年,他们采用同样的微机械剥离方法首先成功地制备出了和石墨具有类似的空间结构和成键属性的二维六边形蜂窝构型氮化硼晶体.2近几年来,石墨烯由于结构上的完全二维特征以及良好的导电性,在被制备出来以后就受到了广泛关注.3-6由石墨烯切割形成的具有准一维特性的石墨烯纳米带(GNRs),作为一种新颖的碳基纳米材料,由于随着其边沿形状不同及纳米带宽度的不同而表现出的性质也不同,被认为是未来纳米器件中非常重要的组成材料,因而被大量的研究.7-14在对GNRs的研究中,缺陷及掺杂对其结构和性质的影响一直是一个非常有意义的研究方向,9-14在掺杂元素中,由于B、C、N元素处在元素周期表的同一周期且彼此相邻,在物理、化学性质等方面接近,而受到关注.研究显示,掺杂使得GNRs的能带结构发生变化,材料从金属转变为半导体,13并且对其自旋极化输运性质也产生了影响.14相比之下,另一种与石墨烯纳米带结构类似的材料——硼氮纳米带受到的关注较小,相关的研究也相对较少.研究显示这种六边形蜂窝构型硼氮二维晶体具有良好的电学与光学性质.切割这种二维晶体可以得到不同宽度和边缘指向的硼氮纳米带(BNNRs).同石墨烯纳米带一样,BNNRs可分为armchair型BNNRs(a-BNNRs)和zigzag型BNNRs (z-BNNRs).
目前对硼氮纳米带的研究主要集中在对其电子结构及其调制与材料的光学性质的研究上,15-24研究显示,z-BNNRs的能带具有较大带隙,呈现出半导体的性质,且其带隙随着宽度的增加呈递减趋势,而a-BNNRs的带隙则出现了近周期性的震荡,18两种纳米带均为半导体性质.鉴于这些优异的电子性质,人们也尝试用各种方法调控氮化硼纳米带的电子结构.18-22研究表明扶手型氮化硼纳米带的带隙会随着外加电场强度的增加而减少,而锯齿型纳米带的会依据电场方向和强度的不同,带隙还有载流子的有效质量也发生较大的变化.但缺陷或掺杂对z-BNNRs的能带结构及其输运性质的影响却很少涉及,有必要进行深入的探讨和研究.本文利用第一性原理方法对氧原子掺杂对z-BNNNRs的能带结构和输运性质的影响进行了探讨,通过计算发现氧原子对氮原子的替代掺杂只对近邻的原子产生较大的畸变,对次近邻的原子影响较小,而氧原子对硼原子的替代掺杂则对近邻和次近邻原子均产生较大的畸变并伴随较大的形成能.因此,文中的掺杂模型选用氧原子对氮原子的替代掺杂.
2 计算方法和模型
能带结构和输运性质的计算采用密度泛函理论和非平衡格林函数的计算程序包SIESTA-3.025完成.其中体系电子能带的计算是采用DZ(Double ξ)基组,平面波截断能取200 eV,自洽场迭代使用简约布里渊区的9×9×1的k点,自洽迭代的收敛精度为10-4;体系输运性质的计算是采用单电子的散射理论26来进行,当两电极施加外部偏压V时,通过体系的电流I为
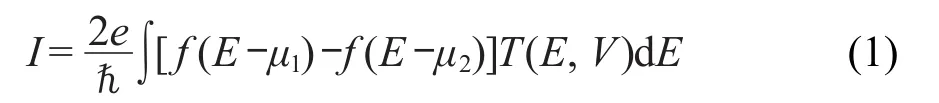
式中:e为电子电量,ℏ为Plank常数,f(E)为Femi-Dirac分布函数.施加外部偏压V=μ1-μ2,μ1、μ2分别为左、右电极的化学势.T(E,V)为电子从一个电极流向另一个电极的穿透函数,E为电子能量.其具体公式为

式(2)中:Tr表示矩阵求迹,Γ1、Γ2为左、右电极与散射区分子间的耦合作用,具体公式为

其中:Im表示虚部,Σ1(2)为左右电极的自能矩阵,gs为电极表面的格林函数矩阵,τ为左右电极与散射区的相互作用函数,G为体系的格林函数矩阵,具体公式为

式中:E为单位矩阵,H为散射区分子的哈密顿矩阵,S为电极表面积.通过上面的公式,就可以计算出体系的伏安特性.
BNNRs的宽度和长度用(m,n)标定,沿宽度方向一排硼氮原子的总个数定义为宽度m,沿长度方向的最小周期性单元重复的数目定义为长度n, BNNRs边缘的悬挂键用氢原子饱和.
3 计算结果与讨论
3.1 纯净z-BNNRs体系的能带结构
图1(a)给出了宽度m为4的z-BNNRs费米面附近的能带结构,带隙为4.3544 eV,可以看出,z-BNNRs呈现宽带隙半导体性质;图1(a)中的插图则给出了带隙大小随m的变化关系.从图中可以看出,随着宽度的增加,带隙大小是呈下降趋势的,这与文献18报道的结果相同.
3.2 O掺杂z-BNNRs体系的能带结构

图1 纯zigzag(4,8)型BNNRs(a)和氧掺杂(3.125%)的zigzag(4,8)型BNNRs费米面附近的能带结构(b)Fig.1 Band structures of pure zigzag(4,8)BNNRs(a)and oxygen-doping(3.125%)zigzag(4,8)BNNRs(b) near Fermi surfaceThe variation of band gaps of z-BNNRs is drawn as a function of width in the inset.m:the width of BNNRs manobelts
为研究O掺杂对z-BNNRs电子能谱的影响,我们以宽度为2的z-BNNRs做为研究模型,首先考虑了外来掺杂原子对体系构型的影响,通过对掺杂体系的充分弛豫发现O原子对z-BNNRs中N原子的替代掺杂对近邻的三个B原子产生较大的畸变,而对次近邻的N原子则影响较小,弛豫的结果与文献27中的计算结果相一致.在以下能带计算和输运性质的计算中对于掺杂体系均采用完全弛豫后的结构体系.图1(b)给出了O掺杂zigzag型BNNRs费米面附近的能带结构,从图中可以看出,O原子对z-BNNRs中N原子的替代掺杂在费米面处引入一对局域的杂质能带(图1(b)中能带α,β),能带β为空带,而能带α被部分占据改变了体系的导电性能,实现了体系从宽带隙的半导体到金属的转变.
3.3 掺杂z-BNNRs体系的输运性质
3.3.1 掺杂位置对体系输运性质的影响
通过之前的讨论可知,O掺杂使体系产生了从半导体到金属的转变,所以在讨论O掺杂z-BNNRs的输运性质时,左右电极均采用O掺杂的z-BNNRs,所采用的模型如图2所示.首先考虑是掺杂浓度为3.125%的情况下掺杂位置在对于z-BNNRs体系的影响,图3(a)显示了O掺杂浓度为3.125%,掺杂位置分别位于纳米带边缘和纳米带中间的z-BNNRs的I-V曲线,从图中可以看到两种位置的O掺杂均使z-BNNRs在[-1.5,1.5]偏压区间内呈现出负微分电阻行为.当O掺杂在纳米带中间位置,在偏压区间[-1.5,1.5]的±0.3 V对称位置各出现一个峰值,峰值的大小分别为9.4和-8.0 μA;而当O掺杂在纳米带的边缘位置,在偏压区间[-1.5,1.5]的0.4、0.8 V和-0.3、-1.0 V四个位置各出现大小两个峰值,峰值分别为10.5、3.1 μA和-6.8、-2.6 μA.为更好地理解掺杂位置对于体系输运性质的影响,我们也做出了掺杂O原子浓度为3.125%时两种掺杂位置(边缘与中间)的z-BNNRs的dI/dV微分电导随偏压V的变化曲线,如图3(b)所示.从图3(b)可见边缘掺杂和中间位置掺杂均在[-1.5,1.5]偏压区间出现两次负微分电阻行为,边缘掺杂出现负微分电导峰值要比中间位置出现的更大.综上所述,掺杂位置的不同使得体系的输运性质产生了较大的变化,这一点与硼掺杂一维带帽碳纳米管分子结构的电子输运特性较为相似,该体系中硼的掺杂位置在计算的偏压范围内对输运性质亦有较为明显的影响.28
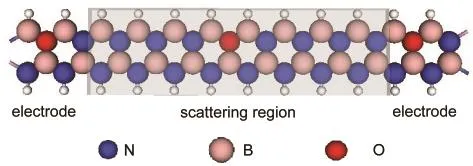
图2 氧掺杂z-BNNRs体系输运计算结构图Fig.2 Schematic description for the calculation of oxygen-doping z-BNNRs systemʹs transport properties

图3 氧原子掺杂浓度为3.125%时掺杂位置分别为带边缘和中心的zigzag(2,8)型BNNRs的输运特性曲线Fig.3 Transport properties of edge-doping zigzag(2,8)BNNRs and middle-doping zigzag(2,8)BNNRs with the oxygen atomic concentration of 3.125%(a)I-V characteristic curves;(b)variations of differential coefficient(dI/dV)versus voltage
为了进一步研究O掺杂位置对z-BNNRs输运性质的影响,解释观测到的负微分电阻行为随掺杂位置的变化,我们分别计算了O掺杂浓度为3.125%,掺杂位置分别位于纳米带边缘和中间的z-BNNRs在0.3、0.5、0.8和1.5 V偏压下的透射谱,结果如图4所示.从公式(1)可以看出,电流是由偏压窗口内T(E,V)的积分面积决定的,对于0.3 V偏压下透射谱,偏压窗口内的有效积分面积均比较大,且相差较小,对应于I-V曲线中较大的峰值位置;而对于0.5 V偏压下透射谱,纳米带边缘掺杂的偏压窗口下的有效积分面积明显小于纳米带中间掺杂的透射谱,所以对于边缘掺杂在0.5 V偏压下出现电流的谷值;随着偏压的增大,在0.8 V偏压下边缘掺杂和中间掺杂的透射谱的偏压窗口内的有效积分面积几乎相同,不过对于边缘掺杂0.8 V偏压下为其I-V曲线峰值较小的位置;在1.5 V偏压位置已经超出负微分电阻出现的区间范围,边缘掺杂和中间掺杂的透射谱几乎相同.可见,从不同偏压下的透射谱的变化趋势也反映出O原子对BNNTs纳米带中N的替代掺杂,由于位置的不同(边缘掺杂和中间掺杂)对体系的输运性质产生较大的影响,边缘掺杂能够产生更大的负微分电导.
3.3.2 掺杂浓度对体系输运性质的影响

图4 氧原子掺杂浓度为3.125%时掺杂位置分别位于纳米带边缘(a)和中间(b)的zigzag(2,8)型BNNRs在不同偏压下的透射光谱Fig.4 Transmission spectra with different bias voltages of edge-doping(a)zigzag(2,8)BNNRs and middle-doping(b)zigzag(2,8)BNNRs with the oxygen atomic concentration of 3.125%The zero of energy is set to the Fermi energy.The windows of bias are demonstrated with grey color.
为考虑浓度对体系输运性质的影响,我们也计算了在纳米带宽度一定的情况下,掺杂O浓度为3.125%、4.167%和6.250%的z-BNNRs的I-V曲线,如图5(a)所示.从图中可以看出,O掺杂浓度分别为4.167%和6.250%的z-BNNRs的I-V曲线的变化趋势大致相同,均在[-1.5,1.5]偏压范围两次呈现出负微分电阻行为,且其峰值的位置和大小产生较小的变化;对于掺杂浓度为4.167%的体系在正偏压区间-0.3和-0.8 V位置出现9.0和10.0 μA的峰值,在负偏压区间0.3和1.0 V位置出现10.0和8.1 μA的峰值;而对于掺杂浓度为6.250%的体系,在正偏压区间0.3和0.7 V位置出现8.0和8.6 μA的峰值,在负偏压区间-0.3和-0.7 V位置出现9.7和5.8 μA的峰值.为更好地理解不同掺杂浓度下的体系输运性质的变化,我们给出三种浓度下的dI/dV微分电导随偏压V的变化曲线,如图5(b)所示.由图5(b)中可以看出,随着掺杂浓度的增加,负微分电导的最大值也随之增大;这个变化与前面所述掺杂位置对体系输运性质的影响是相一致的,因为随着掺杂浓度的增加,掺杂原子的位置也越发靠近散射区的边缘位置,而边缘位置掺杂能够使得体系呈现更大的负微分电导.O/N替代掺杂在z-BNNTs体系由于掺杂位置或浓度的不同所引起的负微分电阻变化的特性在微电子器件的分子开关上将有着潜在的应用.
3.3.3 体系长度及宽度对输运的影响

图5 氧原子掺杂浓度为3.125%、4.167%、6.250%时z-BNNRs的输运特性曲线Fig.5 Transport properties of O-doping zigzag(2,8)BNNRs with the oxygen atom concentrations of 3.125%,4.167%,and 6.250%(a)I-V characteristic curves;(b)variations of differential coefficient(dI/dV)versus voltage

图6 不同氧原子掺杂浓度和不同长度和宽度的z-BNNRs的I-V曲线Fig.6 I-V characteristic curves of O-doping zigzag with different doping concentrations of oxygen atoms and different O-doping zigzag lengths and widths(a)O-doping zigzang(2,8)BNNRs and O-doping zigzag(2,4)BNNRs with the concentration of oxygen atoms of 6.250%; (b)O-doping zigzag(2,6)BNNRs and O-doping zigzag(3,6)BNNRs with the concentration of oxygen atoms of 4.167%. n and m represent the length and the width of BNNRs,respectively.
在之前的计算和讨论中可知掺杂位置和掺杂原子的浓度均对z-BNNRs体系的输运性质产生较大的影响,接下来我们考虑在掺杂浓度和位置确定的情况下,中间散射区宽度变化对体系输运性质的影响.这里分别计算了在掺杂浓度为6.250%的情况下,长度n分别为8和4的体系的输运特性,而体系的宽度不变均保持为m=2,I-V曲线如图6(a)所示.从图中可以看出,长度变化的两种体系都存在负微分电阻现象,对于长度较小的体系,峰值大小反而有所增大,随着长度的增加,掺杂原子的位置越发远离散射区的边缘,所以长度较短的体系能产生较大的微电流峰值,这点是与前面位置掺杂所讨论的边缘掺杂能导致较大的电流峰值的结论是相一致的.
考虑了散射区长度变化对输运性质的影响后,我们又考虑散射区宽度对于体系输运性质的影响,分别计算了掺杂浓度均为4.167%,宽度分别为2和3,而长度保持为n=6不变的体系的输运特性,I-V曲线如图6(b)所示.从图中可以看出,宽度变化的两种体系都存在负微分电阻现象,宽度较小的体系反而微电流峰值有所增大,随着宽度的增大,掺杂原子的位置越发远离体系的边缘,宽度较小掺杂位置愈靠近散射区的边缘,宽度较小的体系与前面位置掺杂所讨论的边缘掺杂能导致较大的微电流峰值的结论是相一致的.
4 结论
采用第一性原理和非平衡格林函数方法对O掺杂z-BNNNRs的能带结构及输运性质进行了研究.研究发现,O掺杂将使z-BNNNRs能带结构发生变化,材料从半导体转变为金属;O掺杂明显地改变了z-BNNNRs体系的导电性能,在一定的偏压范围内产生明显的负微分电阻现象,边缘掺杂能够比中间掺杂产生更大的负微分电导,进一步的输运性质计算给出的透射谱也印证了这一点.随着掺杂浓度的增加,负微分电导的极值也随之增大,同时长度和宽度的变化也对掺杂体系的输运性质产生一定的影响,与掺杂位置所导致的变化是一致的.O掺杂在zigzag型BNNNRs体系引起的负微分电阻变化的特性在微电子器件的分子开关上将有着潜在的应用,将有助于基于BNNRs的功能器件的设计.
(1) Novoselov,K.S.;Geim,A.K.;Morozov,S.V.;Jiang,D.; Zhang,Y.;Dubonos,S.V.;Grigorieva,I.V.;Firsov,A.A. Science 2004,306,666.
(2) Novoselov,K.S.;Jiang,D.;Schedin,F.;Booth,T.J.; Khotkevich,V.V.;Morozov,S.V.;Geim,A.K.Proc.Natl. Acad.Sci.U.S.A.2005,102,10451.
(3) Novoselov,K.S.;Geim,A.K.;Morozov,S.V.;Jiang,D.; Katsnelson,M.I.;Grigorieva,I.V.;Dubonos,S.V.;Firsov,A. A.Nature 2005,438,197.
(4) Zhang,Y.;Tan,Y.W.;Stormer,H.L.;Kim,P.Nature 2005,438, 201.
(5) Geim,A.K.;Novoselov,K.S.Nat.Mater.2007,6,183.
(6) Castro,N.A.H.;Peres,N.M.R.;Novoselov,K.S.;Gein,A.K. Rev.Mod.Phys.2009,81,109.
(7) Son,Y.;Cohen,M.L.;Louie,S.G.Phys.Rev.Lett.2006,97, 216803.
(8) Son,Y.;Cohen,M.L.;Louie,S.G.Nature 2006,444,347.
(9) Ouyang,F.P.;Xu,H.;Wei,C.Acta.Phys.Sin.2008,57,1073. [欧阳方平,徐 慧,魏 辰.物理学报,2008,57,1073.]
(10) Ouyang,F.P.;Xu,H.;Li,M.J.;Xiao,J.Acta.Phys.-Chim.Sin. 2008,24,328.[欧阳方平,徐 慧,李明君,肖 金.物理化学学报,2008,24,328.]
(11) Ouyang,F.P.;Wang,H.Y.;Li,M.J.;Xiao,J.;Xu,H.Acta. Phys.Sin.2008,57,7132.[欧阳方平,王焕友,李明君,肖金,徐 慧.物理学报,2008,57,7132.]
(12) Ouyang,F.P.;Wang,X.J.;Zhang,H.;Xiao,J.;Chen,L.N.; Xu,H.Acta.Phys.Sin.2009,58,5640.[欧阳方平,王晓军,张 华,肖 金,陈灵娜,徐 慧.物理学报,2009,58,5640.]
(13) Lin,Q.;Chen,Y.H.;Wu,J.B.;Kong,Z.M.Acta.Phys.Sin. 2011,60,97103.[林 琦,陈余行,吴建宝,孔宗敏.物理学报,2011,60,97103.]
(14) Zheng,X.H.;Dai,Z.X.;Wang,X.L.;Zeng,Z.Acta.Phys.Sin. 2009,58(Special issue),S259.[郑小宏,戴振翔,王贤龙,曾 雉.物理学报,2009,58(专刊),S259.]
(15) Watanabe,K.;Taniguchi,T.;Kanda,H.Nat.Mater.2004,3, 404.
(16) Arnaud,B.;Lebègue,S.;Rabiller,P.;Alouani,M.Phys.Rev. Lett.2006,96,26402.
(17) Li,J.;Gui,G.;Zhong,J.X.Journal of Applied Physics 2008, 104,94311.
(18) Zhang,Z.H.;Guo,W.L.Phys.Rev.B 2008,77,75403.
(19) Du,A.J.;Smith,S.C.;Lu,G.Q.Chem.Phys.Lett.2007,447, 181.
(20) Chen,Z.G.;Zou,J.;Liu,G.;Li,F.;Wang,Y.;Wang,L.;Yuan, X.L.ACS Nano 2008,2,2183.
(21) Park,C.H.;Louie,S.G.Nano Lett.2008,8,2200.
(22) Barone,V.;Peralta,J.E.Nano Lett.2008,8,2210.
(23) Jin,C.H.;Lin,F.;Suenaga,K.;Lijima,S.Phys.Rev.Lett.2009, 102,195505.
(24) Gui,G.;Li,J.;Zhong,J.X.Phys.Rev.B 2008,78,75435.
(25) Brandbyge,M.;Mozos,J.S.;Ordejón,P.;Taylor,J.;Stokbro,K. Phys.Rev.B 2002,65,165401.
(26) Datta,S.Electronic Transport in Mesoscopic Systems; Cambridge University Press:Cambridge,1995;pp 117-163.
(27) Silva,L.D.A.;Guerini,S.C.;Lemos,V.;Filho,J.M.IEEE Trans.Nanotechnol.2006,5,517.
(28) Zhao,P.;Liu,D.S.Chin.Sci.Bull.2010,55,4104.
October 13,2011;Revised:November 28,2011;Published on Web:December 7,2011.
Effect of O/N Substitutive Doping on the Band Structure and Transport Properties of the zigzag Boron Nitride Narrow-Nanoribbons
CHEN Yu-Hang ZHANG Chao-Min WU Jian-Bao*LIN Qi
(College of Fundamental Studies,Shanghai University of Engineering Science,Shanghai 201620,P.R.China)
By performing first-principles calculations and non-equilibrium Greenʹs function,the energy band structure,transmission spectrum and current-voltage characteristics of the O-doping zigzag boron nitride narrow-nanoribbons(z-BNNNRs)were investigated.The calculation results show that O-doping remarkablychangesthez-BNNNRsenergybandstructureandtransform thematerialfrom a semiconductor to a metal.It is also demonstrated that the system exhibits an obvious negative differential resistance(NDR)characteristic.Further investigations revealed that the position and concentration of O-doping also affected the NDR behavior over a certain range of bias.The negative differential conductance(NDC)for edge-doping is greater than that for middle-doping and the maximum of the NDC increases with an increase of the concentration of O-doping.This special electronic transport property of O-doping z-BNNNRs makes it more suitable as a candidate for molecular devices.
BN nanoribbon;O-doping;Energy band structure;Transport property;Negative differential resistance
10.3866/PKU.WHXB201112071
O641
∗Corresponding author.Email:wujianbao@sues.edu.cn;Tel:+86-21-67791039.
The project was supported by the National Natural Science Foundation of China(11047164),Shanghai College Foundation for Excellent Young Teachers of China(gjd10023),andAcademic Program of Shanghai Municipal Education Commission,China(11XK11,2011X34).
国家自然科学基金(11047164),上海市高校选拔培养优秀青年教师科研专项基金(gjd10023)和上海市教委学科建设项目(11XK11,2011X34)资助

