幂级数在函数方面的应用

袁 炜，贺 欣

(郑州铁路职业技术学院，河南 郑州 450052)

1 引言

我们在数学分析中已经掌握和了解了一些有关幂级数的定义和性质，知道了幂级数是函数项级数中最基本的一类;幂级数的特点是在其收敛区间上绝对收敛，且幂级数在收敛半径范围内可任意次的求导和求积分，又可任意交换求和次序．因此，在此范围内幂级数与多项式一样简便．我们先来看一下幂级数的定义和一些相关的性质．

幂级数的基本性质为:

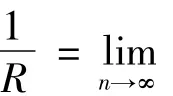
性质 1．4［2］:在收敛半径范围内，即在( － R，R)上，幂级数可任意次逐项求导或求和且产生的新幂级数的收敛半径不变．

知道了幂级数的性质，我们可以看出幂级数是一类最简单的函数项级数，从某种意义上说，它也可以看作是多项式函数的延伸，幂级数在理论和实际上有很多应用，特别是在应用它表示函数方面，有许多方便的运算性质，因此，它在研究函数的方面成为了一个很有用的工具，使我们对它的作用有了新的认识．我们来看一下幂级数在函数中的一些应用．

2 幂级数在函数方面的应用

当f(x)的原函数不能用初等函数的有限形式表示出来时，计算f(x)的定积分就遇到了困难，现在，可以利用幂级数取有限项的办法近似计算这些定积分的值．

2．1 幂级数在计算积分中的应用

我们在计算积分时，当具体要求被积函数能够展成收敛的幂级数，且积分限必须在幂级数的收敛域之内，然后利用逐项积分来计算所求定积分的值．

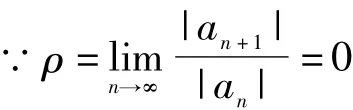
∴收敛半径为R=+∞，这里用到了性质1．2，所以:

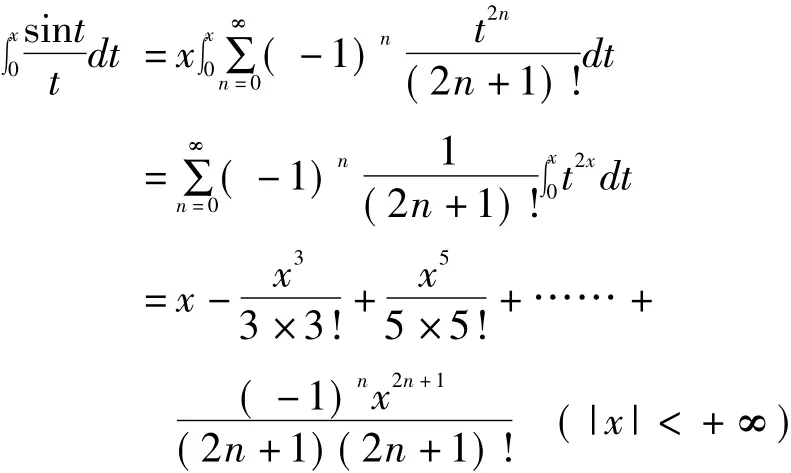
2．2 用幂级数来计算级数的和

我们在求级数的和时，要利用幂级数的性质1．4:幂级数在收敛区间内可逐项求导与逐项求积分，由此可计算级数的和．

则由幂级数逐项微分的性质可知:

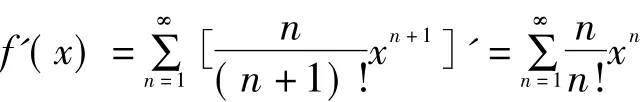
由幂级数逐项积分的性质有:

2．3 用幂级数的性质证明一些不等式

我们可以通过利用幂级数的展开式和性质来证明一些不等式

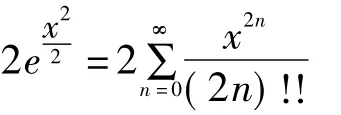
2．4 幂级数在近似计算中的应用

解:数ex的麦克劳林级数是， x∈R．

只需n＞5，由此可知当取项数为n≥6就可满足题目要求

则它在积分区间［0，1］上是连续的，利用sin x的展开式［1］得:

这是交错级数，每项绝对值数列单调减少趋于0，取前三项的和作为近似值，则误差为:

2．5 用幂级数形式来表示某些非初等函数

有些连续函数的原函数和有些常微方程的解不是初等函数，即非初等函数，可用幂级数表示这些原函数的解

问题1:求连续函数e－x2的原函数F(x)

解:e－x2

令 x= －t2，有

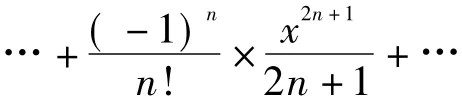
对幂级数在收敛区间内逐项求积分，可得幂级数在理论上和实际中都有很多应用，通过幂级数的展开式来表示函数．利用幂级数和函数的分析性质．常常能够解决数学分析中很多难题．由于它结构简单，因而成为计算常用函数．如指数函数、对数函数、三角函数和很多超越函数的一个基础工具．

［1］华东师范大学数学系．数学分析［M］．北京:高等教育出版社，1990．6．

［2］姚允龙．数学分析［M］．上海:复旦大学出版社，2002．8．

［3］裴礼文．数学分析中的典型问题与方法［M］．北京:高等教育出版社，1983．