改进的Mean-Shift遥感影像分割方法
周家香,朱建军,马慧云,梅小明
(中南大学 地球科学与信息物理学院,湖南 长沙,410083)
国内外在图像分割方面已取得了很多成果,现有自然图像分割方法可概括为以下几个方面:基于全局信息或局部信息;基于区域或边缘;针对灰度影像或纹理影像[1]。由于遥感影像所记录地物的复杂性和多样性,数据量巨大,将这些分割方法引入到遥感影像分割中面临很大困难[2−3]。Mean-Shift (MS)算法是一种高效的统计迭代算法,依靠特征空间样本点的统计特征,不需要任何先验知识,近年来被广泛地应用于图像分割[4−7]和跟踪[8]等计算机视觉领域。传统MS算法的计算复杂度是O(kdN2) (其中k为每个数据点的平均迭代次数,d为数据维数,N为1幅图像的像素)[9−12],如IKONOS和QuickBird等遥感影像,需要多次迭代才能收敛。同时,若所用的特征向量的维数多,则收敛速度比较慢,影响遥感图像的实际应用。近年来,一些研究者研究了MS算法的原理,提出减少迭代次数和降低每次迭代的计算量这2种提高算法效率的方法[10]。为了提高MS算法对遥感影像分割的速度和效果,本文提出以下改进措施:
(1) 对不同空间分辨率遥感图像给定空间带宽参考值,不同波段采用不同的灰度值域带宽。基于传统MS算法编写的EDISON软件需要人工输入空间带宽和值域带宽,且所有波段采用相同的值域带宽。若将遥感影像分割成有意义的区域且没有过多的细节,自适应带宽才能得到好的分割效果。
(2) 面对大数据量的遥感影像分割速度慢的问题,本文主要在MS运行效率上采取多项加速措施。
(3) 针对 MS分割存在过分割现象,将检测出的模点采用基于全局模点融合来得到稳定的分割结果。
(4) 可用于遥感影像分割的特征很多,模点检测或模点融合时利用全部特征势必增加计算时间,改进方法将可将特征分组,利用位置和颜色特征进行模点检测,利用纹理特征进行模点融合。
1 改进MS遥感影像分割算法
1.1 传统高斯MS算法模点检测
传统高斯核MS由高斯核密度估计的梯度推导获得[4]。给定d维欧拉空间R中n个采样点{xi,i=1,…,n},利用高斯核函数K (x)= ( 2π)−d/2exp(−x2),则MS迭代向量为:

式中:xs为二维位置特征;xr为多维值域特征;hs为空间带宽;hr为值域带宽。则传统MS计算步骤:
(1) 选用高斯核函数,带宽hs和 hr,随机给定样本点x;
(2) 根据式( 1) 计算样本点的迭代向量m(x);
开展拓展实验是培养学生科学探究能力的有效补充途径。目前高中生物教材中的很多实验为体验或验证性实验,即使是探究性实验,也列出了详细的探究过程与具体内容,学生往往在未经充分思维后就直接参考了教材。因此,教材实验在培养学生自主探究能力上还稍显不足,不能满足热爱生物学科的学生的求知需求和探究愿望,而拓展实验可以作为有效补充。为此,在教学实践中,笔者结合校本课进行了拓展实验教学,积极探索有效开展拓展实验促进学生科学探究能力提升的实施策略。
(3) 条件判断,若|m(x)−x|>ε(ε为阈值,如 0.001),则移动点x到m(x),执行步骤(2),否则,结束循环;
(4) 将结束循环后的 m(x)赋给 x,此时 m(x)称为样本点x的模点;
(5) 移动到下一样本点x,重复步骤(2)~(4),直至检测出影像内每个数据点的模点为止;
(6) 将收敛至相同模点的数据点归为同一区域,得到初分割结果。
这样,整个影像被分解成m个子区域Sj(j=1,2,…,m),每个子区域像素为nj,中心为cj,则:

1.2 全局模点融合
由于MS分割存在过分割问题,经过MS分割后,将以点阵表示的图像转化为块状表示。然后,采用如下过程的基于区域的MS迭代。
对每一个子区域Sj(j=1,2,…,m),进行以下迭代:

式中:np为区域p的像素;h为带宽;k为迭代次数;= c 。用上式进行迭代计算,直至j 为止(εw是阈值,如0.001),将最终收敛值记录为。
1.3 改进的MS遥感影像分割算法实现
1.3.1 滤波
图像噪声会使检测出的局部模点数过多,这样使后面的模点融合变得困难。滤波能降低噪声对模点检测的影响。事实上,MS本身对噪声不太敏感[11],模点检测前的滤波能很好地降低噪声的影响,这样能使模点检测过程更简单。本文选择3×3的中值滤波。
1.3.2 带宽的选择
在MS算法中最重要的参数是带宽矩阵H,它决定迭代速度和分割效果。目前,Plug-in 和Cross-validation是广泛使用带宽选择方法[1]。Plug-in规则是用估计参数来代替未知参数,渐进积分均方误差是应用于Plug-in规则的通用标准。使渐进积分均方误差最小便可估计全局值域带宽:
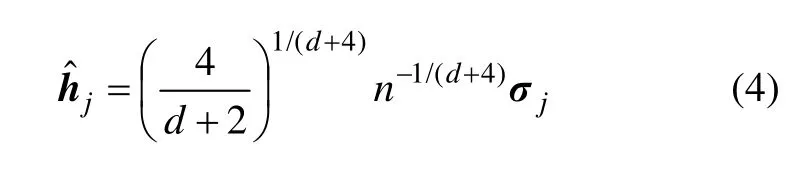
式中:d为特征向量维数;j为单个波段;n为数据量;σj为特征向量的标准差。
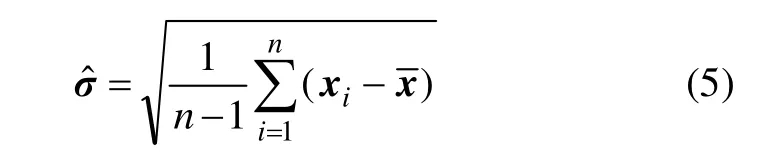
在plug-in准则下获得的值域带宽hr=(hR,hG,hB)能尽可能地降低估计密度函数与原始密度函数之间的变形。为了将遥感影像分割成有意义的区域而不含有过多的细节,一般来说,过小的hr是无意义的。但是,过大的值域带宽导致忽略更多的影像细节,同时降低检测出的模点数;相反,小的灰度带宽使更多的地物细节被提取出来。因此,灰度值域带宽hr被认为是分割的尺度。
1.3.3 快速高斯模点检测
应用传统MS算法进行聚类,可得到初始分割结果。初始分割是对影像中每一个像点进行MS迭代得到其模点,由于遥感影像数据量大,迭代计算量非常大,本文采用以下加速策略。
(1) 以待处理点 xs为中心,事先根据图像的空间分辨率来选择空间带宽hs,以长、宽均为2hs+1的正方形按下式构造高斯空间模板;

式中:xs表示待处理点的二维坐标,xsi为以xs为中心,长和宽为2hs+1正方形内的采样点二维坐标。可以看作权值,与xs点近的采样点权值大,远的采样点权值小。则式(1)变成:
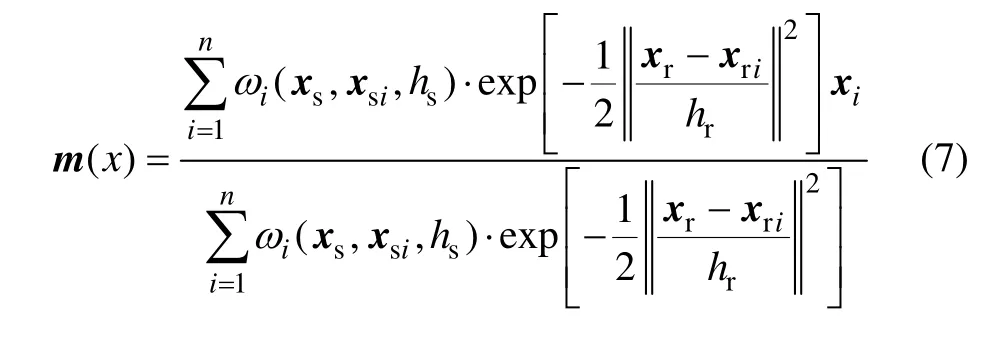
(2) 为了减少MS迭代次数,从xn点开始MS迭代,第 τ次迭代后的向量为等于或近似于另一特征向量xm,则认为xn和xm收敛于同一个模点,停止迭代。
(3) 对任意一随机样本点x,沿一定的路径收敛至一固定点(即模点),将收敛路径一定宽度内的点都认为收敛至相同的模点,这些点不再参加迭代计算。
(4) MS迭代计算量大的1个主要原因是特征向量的维数,而遥感图像可用的特征向量的维数很多,本文将特征向量分为2组,首次迭代时使用多光谱灰度特征,模点融合时使用纹理特征。
1.3.4 基于全局的模点融合
由于传统MS分割一般存在过分割现象,进一步将分割后的影像进行全局模点融合,得到最终分割结果。遥感影像的特征有位置、灰度、纹理、形状等,为了达到理想的分割结果,应尽可能地利用遥感影像的多维特征[9],这样势必会增加计算时间。为了充分利用遥感影像的多维特征又不增加计算时间,在模点融合时使用纹理特征。
此时,用到的纹理特征f1,f2和f3分别为:

式中:i和j为像素点灰度值;p(i,j)为灰度值i和j出现的归一化概率;L为灰度级。则式(3)中h应为纹理带宽ht。对任一分割子区域Sj(j=1,2,…,m),其纹理带宽由下式计算:

式中:nj为第 j块的像素,fki(k=1,2,3)为该块内像素i的 fk纹理特征;ckj(k=1,2,3)为第j块的fk纹理均值。
2 实验结果评价与分析
2.1 分割实验
在改进的分割方法中,空间带宽hs主要影响计算速度。不同传感器的影像有不同的空间分辨率。图1所示为 SPOT5影像采用不同空间带宽分割结果的对比。实验发现,空间分辨率为10.00 m的SPOT5影像选用hs=5比较合适,空间分辩率为2.44 m的Quickbird影像选用hs=9比较合适。
图2(a)是1幅Quickbird 影像270×270的子图像,采用前面提出的参考空间带宽 hs=9和由式(4)计算的灰度值域带宽进行快速高斯MS迭代得到图2(b)所示的分割结果(290个模点)。图2(c)所示是用EDSION软件(1个基于传统MS算法编写的软件)分割结果。将本文的分割结果与EDISON软件分割结果进行对比,由图2(c)可见:本文分割结果要优于EDISON软件分割结果。

图1 SPOT5影像不同空间带宽对比实验Fig.1 Contrast experiment of SPOT5 image with various space bandwidths

图2 改进分割方法与EDISON分割结果对比Fig.2 Comparative segmentation between presented approach and EDISON of Quickbird image
从图2(b)可以看出:本文的分割结果比较理想,但与分割参照图(图3(b))比较还存在过分割现象。对初分割结果进行全局模点融合,保持原有空间带宽不变,采用式(11)计算每块的纹理带宽,得到图3(a)所示的实验结果。由图3(c)可见:本文分割结果比较理想。
2.2 本文改进方法与传统MS算法的时间比较
通过实验比较传统MS方法与本文MS改进方法的算法时间。采用图2(a)所示Quickbird图像,计算时间见表1,从表1可以看出:本文所采用加速策略是有效的。
2.3 分割效果讨论
为了评价分割的效果,本文对图2(a)所示的Quickbird影像进行定量对比实验。Polak等[13]提出了一种基于对象一致性误差(EOC)的客观有效的图像分割评判标准。EOC(Ig,Is)∈[0,1](其中Ig为地面参考对象,Is为实际分割对象)。当EOC=0时,表示分割完全与地面参考对象一致;EOC越小,表示分割效果越好。实验所用图2(a)的研究范围较小,图像空间分辨率较高,且各类地物相对集中,通过目视判读得到实验参考图(图3(b))。将地物分为房屋、林地、水面、农田、绿地以及阴影6类。表2所示为本文方法与EDISON软件分割的EOC,可以看出:采用本文方法所得房屋、林地的分割效果明显优于EDISON的分割效果,水面、农田、绿地和阴影4类地物的分割效果相当。

图3 模点融合后分割结果Fig.3 Segmentation results after mode merging
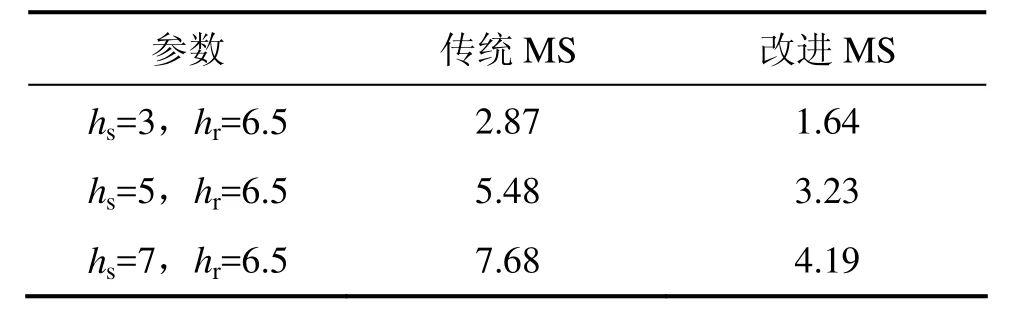
表1 传统MS与改进MS计算时间比较Table 1 Comparative time of traditional MS and improved MS s

表2 改进分割方法与EDISON分割方法的Eoc对比Table 2 Comparison of Eoc between presented improved approach and EDISON
3 结论
(1) 对常用的高分辨率遥感影像如 SPOT5和Quickbird的MS模点检测的空间带宽的选择给出了参考值,其他的遥感影像根据其空间分辨率参照这2类影像来确定。
(2) 遥感影像不同波段分别用公式计算值域带宽,以实现自适应的MS遥感影像分割。
(3) 模点检测时采用 4个有效的加速措施,减少了MS迭代时间;同时,将遥感影像的多维特征分组,模点检测时采用空间特征和多光谱特征,模点全局融合时采用纹理特征,这样加快了MS迭代速度。
(4) 采用基于全局的模点融合提高遥感影像分割精度。用 MATLAB实现了本文改进的遥感图像分割方法,实验结果与由传统算法所得结果相比,本文方法具有分割效果好等优点。
[1]HONG Yi-ping, YU Jian-qiang, ZHAO Dong-bin. Improved mean shift segmentation approach for natural images[J]. Applied Mathematics and Computation, 2007, 185(2): 940−952.
[2]van der Sande C J, de Jong S M, de Roo A P J. A segmentation and classification approach of IKONOS-2 imagery for land cover mapping to assist flood risk and flood damage assessment[J]. International Journal of Applied Earth Observation and Geoinformation, 2003, 4: 217−229.
[3]杨朝云, 陈光儒, 吕嫦艳, 等. 一种改进的高分辨率遥感影像分割方法及应用[J]. 电脑信息技术, 2010, 18(4): 45−48.YANG Zhao-yun, CHEN Guang-ru, LÜ Chang-yan, et al. An improved high resolution RS images partition way and its applying[J]. Computer and Information Technology, 2010, 18(4):45−48.
[4]Comaniciu D, Meer P. Mean-Shift: A robust approach towards feature space analysis[J]. IEEE Transaction on Pattern Analysis and Machine Intelligence, 2002, 24(5): 603−619.
[5]Comaniciu D, Ramesh V, Meer P. The variable bandwidth mean shift and data-driven scale selection[C]//Proceedings of Eighth IEEE International Conference on Computer Vision. Vancouver,United States, 2001: 438−445.
[6]王兆虎, 刘芳, 焦李成. 一种基于视觉特性的遥感图像分割[J]. 计算机学报, 2005, 28(10): 1687−1691.WANG Zhao-hu,LIU Fang,JIAO Li-cheng. A remote sensing image segmentation algorithm based on vision information mean shift algorithm accelerated mean shift algorithm[J]. Chinese Journal of Computers, 2005, 28(10): 1687−1691.
[7]Comaniciu D. An algorithm for data-driven bandwidth selection[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2003, 25(2): 281−288.
[8]Comaniciu D, Ramesh V, Meer P. Real-time tracking of non-rigid objects using mean shift[C]//Proceedings of IEEE Conference on Computer Vision and Pattern Recognition. Hilton Head Island, United States, 2000: 142−149.
[9]Georgescu B, Shimshoni I, Meer P. Mean shift based clustering in high dimensions: a texture classification example[C]//Proceedings of IEEE International Conference on Computer Vision. Nice, France, 2003: 456−463.
[10]Carreira-Perpinan M A. Acceleration strategies for Gaussian mean—shift image segmentation[C]//Proceedings of the 2006 IEEE Computer Society Conference on Computer Vision and Pattern Recognition. New York: IEECS Press, 2006: 543−549.
[11]Kaftan J N. Mean shift segmentation evaluation of optimization techniques[C]//International Conference on Computer Vision Theory and Application. Madeira, Portugal, 2008: 365−374.
[12]Carreira-Perpinan M A. Gaussian mean shift is an EM algorithm[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2007, 29(5): 767−776.
[13]Polak M, ZHANG Hong, PI Ming-hong. An evaluation metric for image segmentation of multiple objects[J]. Image and Vision Computing, 2009, 27: 1223−1227.

