基于经验模态分解的低信噪比探地雷达数据处理

冯德山，戴前伟，余凯,

(1. 中南大学 地球科学与信息物理学院，湖南 长沙，410083；2. 水利部黄委会勘测规划设计研究院，河南 郑州，450003)

在探地雷达(Ground penetrating radar，GPR)的探测过程中，由于地下介质结构复杂、物性参数迥异和各种噪声、杂波干扰的存在，导致雷达波在地层中传播时变得十分复杂[1]。因此，如何有效地对GPR这种非平稳、非线性信号[2]进行处理，突破以处理稳态数据为主的Fourier变换制约，成为GPR实际应用中亟待解决的问题。柳刚等[3]应用小波变换对低信噪比雷达信号进行处理，论述了小波变换在处理低信噪比的瞬变信号的优势；张志禹等[4]对雷达记录进行小波分解并结合KL变换实现了目标回波信号的串扰抑制；吴宝杰等[5]应用S变换进行雷达数据处理，去除了部分噪声干扰，突出有效信号；吴健生等[6]应用 Radon变换对GPR剖面中存在的“X”形同相轴等线段形进行处理，消除了旁侧干扰影响等。以上时频方法在一定程度上提高了雷达的数据解译精度，但大都属于小波变换或以傅里叶变换为其最终理论依据，仍存在各自难以克服的缺点。以小波变换为例，虽然它具备了多分辨的性质，但仍存在预选小波基函数、软硬阈值参数设置等制约因素，限制了小波变换在GPR信号处理中的应用和推广。经验模态分解 (Empirical mode decomposition，EMD)是一种分析非线性非平稳信号的新方法[7−8]。它首先利用EMD方法将信号分解为若干固有模态函数(Intrinsic mode function，IMF)，然后，将 Hilbert变换作用在每一个 IMF上，得到相应的Hilbert瞬时谱，通过分析各个分量及其Hilbert谱，揭示原信号的多尺度振荡变化特征。它既能使信号分解具有唯一性，又能在时域和频域同时具有良好的局部化性质。利用 EMD分解对信号分解完毕之后，可以根据工程问题的需要灵活地对信号实现重构。它没有先验的变换函数，但是，它具有小波变换的多分辨率性质，又不需要像小波那样考虑小波基的选取问题。经过十几年的发展，EMD分解在海洋气象过程[9]、光谱数据预处理[10]、地球物理[11]等领域得到了广泛研究和应用。Flandrin等[12]通过对高斯白噪声的分析，发现EMD方法表现为时域的二进滤波；Wu等[13]把EMD应用于基于噪声统计规律的去噪；Damerval等[14]提出了二维EMD快速算法；汤井田等[15]应用EMD分解对大地电磁信号进行工频干扰抑制和基线飘移矫正；段生全等[16]以地震资料为应用实例，在物理意义、精确性和自适应性方面全面比较了EMD分解(HHH变换)、Fourier 变换和小波分析法异同及优劣；余志雄等[17−18]运用Hilbert变换将探地雷达实信号转换成复信号，分别提取瞬时振幅、瞬时相位、瞬时频率波形图，形成3个参数独立剖面，提高了雷达解释精度。在此，本文作者首先对低信噪比GPR信号进行EMD分解，得到从高频至低频的GPR信号的IMF分量，通过消去属于噪声部分的本征模态函数分量，达到提高GPR数据信噪比的目的；然后，对去噪后的雷达剖面进行重构，再利用Hilbert变换求取GPR复信号，并提取瞬时振幅、瞬时相位、瞬时频率3个参数，形成3个相互独立的剖面，通过多参数波形剖面相互参照、综合分析，避免了使用单一时距剖面分析所造成的解释偏差。它与传统复信号分析方法不同之处在于输入的信号是经过EMD分解之后的GPR信号，能根据信号处理的目的，针对性地去除低信噪比中各种噪声，在赋于瞬时参数物理意义的同时，提高了GPR数据的解析精度。

1 经验模态分解原理

经验模态分解(EMD)是Hilbert-Huang变换的关键组成部分，它有3个假定条件[19]：

(1) 待处理的信号中至少存在1个极大值和1个极小值。

(2) 由极值点间的间隔决定特征时间尺度。

(3) 若数据序列仅仅包含有拐点，可通过求 1阶或者多阶导数来确定极值点，并且最终结果也可由求积分来获得。

在满足了3个假定条件后，经验模态分解方法认为所有的信号都可由不同的本征模态函数IMF组成，其中，任意1个IMF都可以是线性的或者是非线性的。IMF都必须满足以下2个条件：

(1) 对于 1列数据，极值点和过零点的个数都必须相等或者至多相差1点。

(2) 在任意点，由局部极大点和极小点构成的 2条包络线的平均值为0。每个IMF可以认为是信号中固有的1个模态函数。

EMD的具体实现步骤可描述如下：设信号序列为f(t)，首先找出 f(t)中所有的极大值点和极小值点，通过三次样条拟合，获得f(t)的上包络线u1(t)和下包络线v1(t)，计算上、下包络线在每点的平均值，从而获得1条平均值曲线 m1(t)。用原始信号 f(t)减去所得到的均值，得到1个新的数据序列h1(t)：

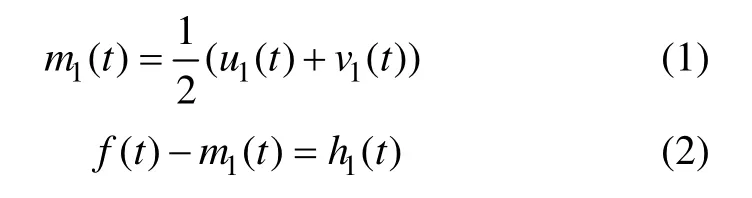
根据上面给出的IMF的判定条件对新的数据序列h1(t)进行判定。若 h1(t)不满足判定条件，则它不是 1个IMF分量序列，为此，重复进行上述处理过程n次，使所得的hk(t)满足IMF的判定条件，此时，hk(t)就是第 1阶(IMF)c1(t)，这个分量代表信号 f(t)中的最高频率分量。然后，原始信号f(t)减去c1(t)，则可以得到去掉了高频部分的差值信号序列r1(t)：

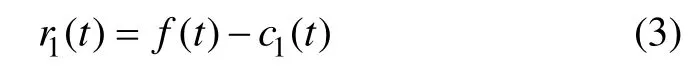
此时，将r1(t)作为待处理的原始数据序列，重复上述步骤，这样，就可以得到第2个IMFc2(t)。重复操作n次，则可以得到n个本征模态函数分量，即：

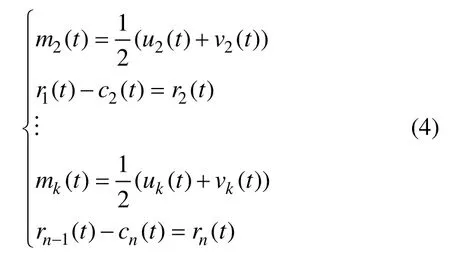
当rn(t)变成了1个常量或者成为1个单调函数时就停止运算。原始信号f(t)可以表示为所有的IMF及剩余量之和：

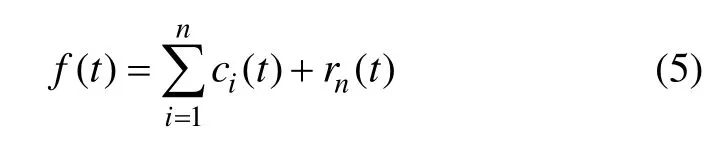
式中：rn(t)为最后得到的残余函数(单调函数)，它代表了信号的平均趋势。所有IMF分量都反映了信号的特征尺度，其尺度依次由小到大。所以，各个IMF分量相应地包含了由高到低不同频率段的成分，代表非线性形号的内在模态特征，它随着信号本身的变化而变化。

2 复信号分析理论

复信号分析又称解析信号分析，就是把与记录道相关的信息在时间域上直接分解为瞬时振幅、瞬时相位、瞬时频率的一种处理和解释技术[20]。在进行复信号分析之前，首先要进行Hilbert变换。Hilbert变换能有效、真实地获取信号中所含的有效信息，它本质上是一个全通滤波器[20]。设输入的GPR信号为x(t)，它是经过EMD分解并去噪处理的，通过滤波器H(ω)滤波后输出信号为xˆ(t)。若H(ω)具有的幅频特征是全通型的且相频具有－90°相移，则

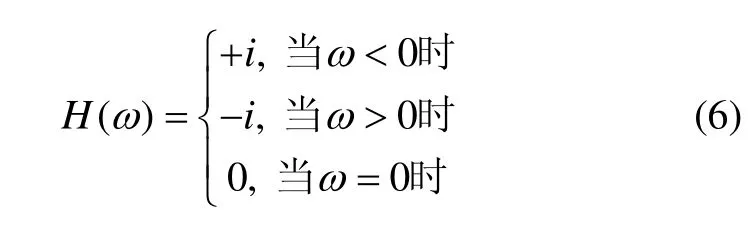
这时滤波器的输出 xˆ(t)称为x(t)的Hilbert变换。显然，xˆ(t)与 x(t)正交。滤波器 H(ω)称为 Hilbert滤波器。x(t)的 Hilbert变换可以记作 xˆ(t)或者 H·x(t)。而 xˆ(t)的定义为：

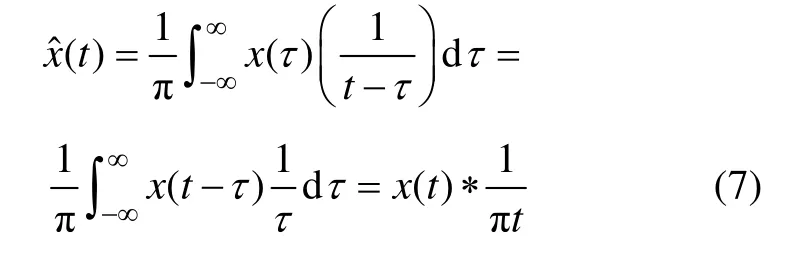
将 x(t)和它的 Hilbert变换xˆ(t)结合起来，组成 1个复信号，即[21]：

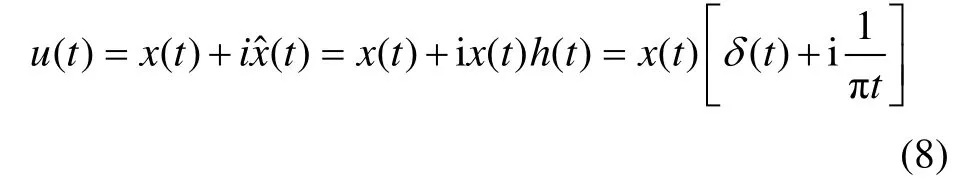
式中：u(t)为x(t)的复信号，又称为解析信号。由于x(t)可以分解为三角函数形式，设x(t)=A(t)cos[ω0t+φ(t)]，(t)亦可表示为(t) = A(t) sin [ ω0t+ ϕ (t )](其中 ω0=2πf)，因此，x(t)的复信号又可表示为：

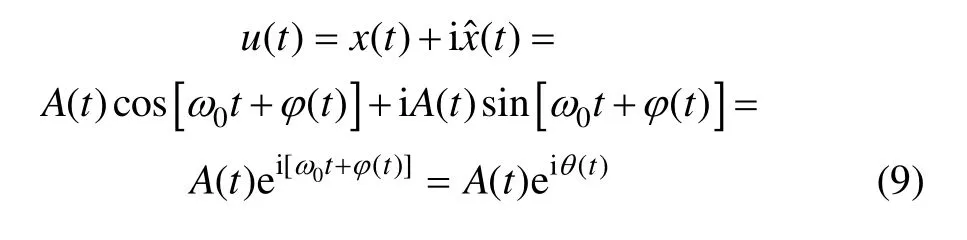
显然，A(t)和 q(t)都随时间而变化。A(t)称为 u(t)的瞬时振幅；θ(t)=ω0t+φ(t)称为u(t)的瞬时相位，相位的时间变化率为

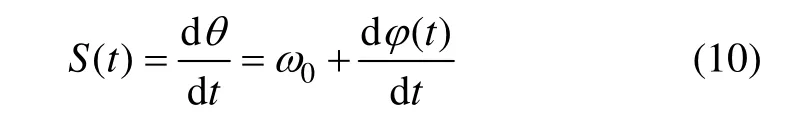
S(t)即为所谓u(t)的瞬时频率。当φ(t)不变或变化不大时，φ′(t)可视为0或常数C，即S(t)=ω0+C只与频率有关。

对于瞬时振幅、瞬时相位和瞬时频率，可以用以下方法计算：首先由EMD分解后的GPR记录x(t)经Hilbert变换求得ˆ(t)，然后计算瞬时振幅：

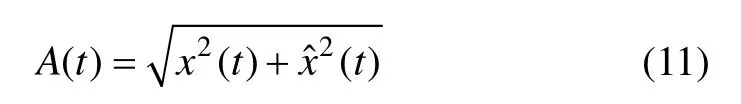
瞬时振幅是时间变量t的函数，与相位θ(t)无关。瞬时相位为

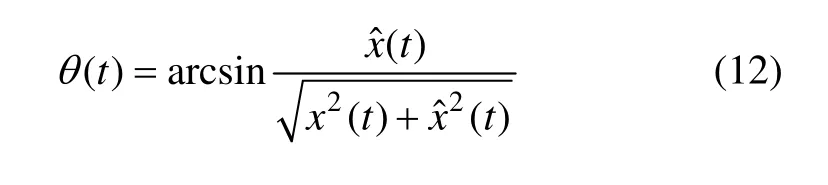
或

瞬时频率 S(t)是瞬时相位函数对时间的变化率，即对θ(t)求导得：

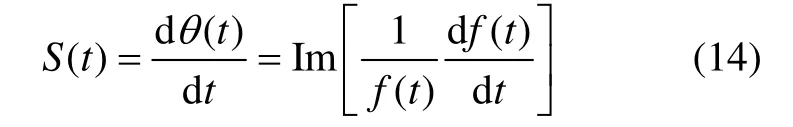
复信号分析技术可以将GPR记录中的瞬时振幅、瞬时相位和瞬时频率分离出来，同一GPR的3个参数瞬时谱从不同的角度反映地下介质的特性。瞬时振幅是对电磁波反射强度的量度，与该时刻GPR信号总能量的平方根成正比，利用这种特征可以对特殊岩层的变化作出判定。当地层中存在有比较明显的分层、空隙或者是地下水的分界面时，在瞬时振幅剖面图中会看到非常明显的异常反应。瞬时相位是GPR剖面上同相轴连续性的量度。雷达波在物性参数相同或相近的地下介质中传播，在相位图中表现出来其相位是连续变化的；而雷达波在物性参数不同或相差较大的地下介质中传播，在异常体处相位会表现出相位错断的强烈反应。瞬时频率所表示的是相位的时间变化率即相位的导数，反映出其相速度。在地层中介质岩性的变化会引起频率的变化，因而利用瞬时频率也作为对地层分界面进行判断的依据。在这3个参数中，瞬时相位谱的分辨率最高，而瞬时频率谱和瞬时振幅谱的变化也较直观，所以，通常根据瞬时频率谱和瞬时振幅谱来确定地下异常或分层的大概位置，然后，利用瞬时相位谱精确确定异常位置和分层轮廓线。有时也可以直接利用瞬时相位谱来确定地下异常的位置。

3 基于 EMD分解的雷达数据处理实例

3.1 单道雷达信号的EMD分解

经验模态分解是自适应的，其分解快速而且有效，同时它又是基于信号的局部变化特性的，所以，特别适合于 GPR这种非线性、非平稳信号的分析。图1所示为1个单道雷达数据EMD分解结果。分析图1中的各个IMF曲线的波形可知：由IMF1到IMF5，频率成分随着分量阶数的增加移向低频；第1阶分量(IMF1)频率最高，首先被提取出来，其中可能包含了高频噪声，余下分量的噪声依次降低，说明 EMD分解具有去除高频噪声的功能；第 2和第 3阶分量(IMF2，IMF3)代表了原雷达道的主要成分，IMF4及其之后的分量相对分量幅值较前3个分量小，不是雷达波的主要成分，余量反映了信号的平均趋势。此外，原始图、IMF1和IMF2中600到800号采样点间反映并明显的异常信息，在IMF3中反映非常清晰、突出，由此可见，经验模态分解还具有分离高、低频异常的作用。

3.2 GPR模拟数据的EMD分解去噪及复信号分析

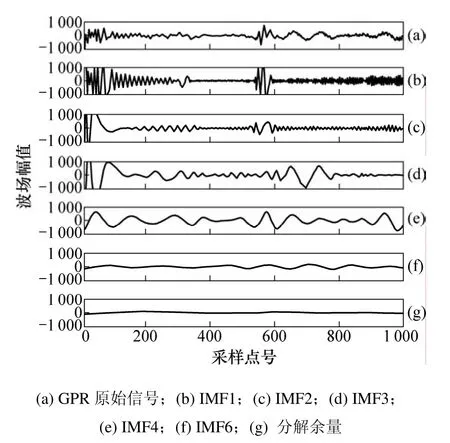
图1 单道GPR信号EMD分解图Fig.1 Single trace GPR signal EMD map

通常使用GPR进行勘探时，干扰普遍存在，如外部噪声的干扰、复杂的地下围岩的干扰等等。因而，在GPR信号处理过程中，如何消除这些干扰并从信号中得到有效的信息，这对于GPR资料的处理及解释有着重大意义。以GPR正演模拟为基础，并在GPR正演数据中加入随机噪声，以分析 EMD分解的去噪效果。设定雷达模型如图2所示，其中：最上层是厚度为0.5 m的空气介质，空气层以下为素填土层，素填土的介电常数为10.0，电导率为0.002 S/m；在素填土层中设置5个金属球状异常体，金属球体的上顶埋度为6.0 m，其电导率为1.0×108S/m，半径为1.0 m，金属球体间距为1.5 m；模拟区域长×宽为20.0 m×10.0 m。脉冲波形为Ricker子波，频率为60 MHz，脉冲位置距上边界0.48 m处，计算的网格长与宽均为0.1 m；时窗为400 ns；采样点从左边0.2 m开始，每隔0.2 m采1个点，采样过程中发送点与接收点是同步移动的，收发距为0.8 m，每道波形有1 024个采样点，共采集了94道雷达数据。采用有限差分法对该模型进行正演，其正演合成剖面如图3所示。图4所示为雷达正演数据加入随机噪声后的剖面。由图4可见：由于绕射现象及随机噪声的存在，导致信号异常混乱，GPR剖面的信噪比与分辨力大大降低。

为此，利用EMD对加噪后的GPR正演剖面进行分解，得到图5所示的分解后的本征模态函数图IMF1～ IMF7。由于EMD分解实际上是一个高通滤波的过程，所以，在对信号的分解过程中高频成分被慢慢滤出，图5(a)～(b)中前2个分离出来的IMF完全是后期加入的高频噪声；图5(c)～(d)中2个IMF是雷达剖面信号的主要成分，其中图5(c)中的 IMF4为金属球体的绕射异常；图5(e)所示为分解得到的IMF7，由于GPR信号的有效部分基本被分离出来，故属于金属球体的异常在图中得不到反映，后面的IMF分量图不再列出。

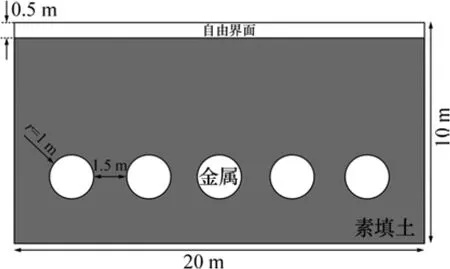
图2 雷达模型示意图Fig.2 Sketch map of GPR model

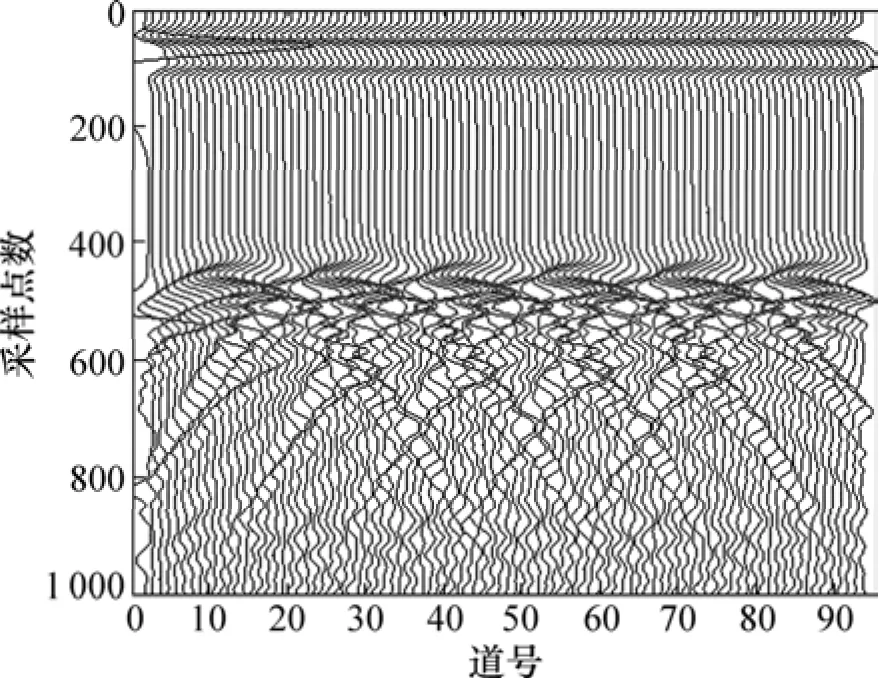
图3 雷达正演剖面图Fig.3 GPR forward simulation map

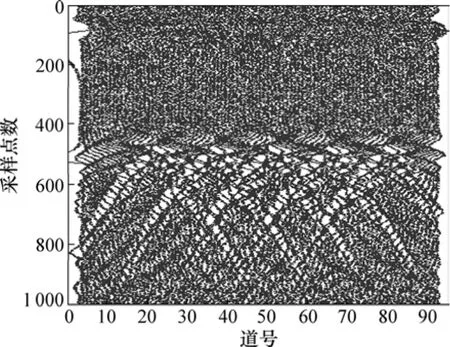
图4 加噪后的雷达正演剖面图Fig.4 GPR forward simulation map of addition noise

通过分析EMD分解结果可知：加入的噪声主要存在于IMF1～IMF2剖面中，为此去除IMF1～IMF2并对其它IMF分量中的有效信号进行重构，重构后的新分量如图5(i)所示。分析图5(i)可知：通过EMD分解后去除主要由噪声组成的 IMF1～IMF2后，大大降低了信号中的噪声干扰，起到了类似滤波的效果。尽管对于GPR剖面的信噪比有较大提高，然而，剖面中异常的显示并不很清晰。为此，在EMD分解的基础上，对重构后的图5(i)信号进行Hilbert变换，分别求得图6所示的GPR瞬时振幅剖面、图7所示的瞬时相位剖面和图8所示的瞬时频率剖面。由于这3个瞬时特征参数所对应地下介质的物性参数不同，其剖面图表像各异，故根据不同的地质状况选择合适的剖面图对信号进行分析比直接利用原始剖面图要更加清晰、有效。对比原始剖面图，瞬时相位图与瞬时频率图更好地反映了异常信息。

3.3 对实测GPR数据进行基于EMD分解的复信号分析

湖南长沙黑麋峰抽水蓄能电站进厂交通隧洞未衬砌的J0+200.00 m～J0+984.00 m段围岩地质条件复杂，需详细查明隧洞中存在的破碎带、裂隙等不良地质体，以确保进出厂人员的作业安全。为此，在该隧洞段开展了探地雷达隐患探测。在探测过程中，采用 GSSI公司生产的 SIR−3000型雷达数据采集单元，选取频率为900 MHz天线，点采样方式，点距为0.20 m，每道扫描512个采样点。

图9(a)所示为该段中比较典型的雷达原始剖面图，可见：由于隧洞中存在的钢拱架、铁丝网、电缆干扰等，导致该原始剖面异常复杂，直观感觉剖面中存在异常体，但又不能准确定位。显然，仅根据该剖面图无法对探测段进行准确的判断和地质解释。为此，先对实测信号进行EMD分解，得到了图9(b)～(e)中分解后的本征模态函数图IMF1～ IMF4(后面分量为无效信号，没有列出)。由于EMD分解实际上是一个高通滤波的过程，信号中的高频噪声成分主要集中在IMF1剖面中，故去除IMF1可达到滤波消噪的目的。图9(f)所示为去除IMF1后的重构图，该剖面中的异常信息比其在原始剖面图中要更加清晰，但仍未达到准确指导异常解释的分辨率。对 EMD分解后的信号进行Hilbert变换，在此基础上，进行复信号分析以提取瞬时特征参数。图10所示为重构后的GPR瞬时振幅剖面，图11所示为重构后的GPR瞬时相位剖面，图12所示为重构后的GPR瞬时频率剖面。对比3种瞬时剖面可知：经过复信号分析处理的GPR剖面更加清晰直观，分辨率更高，由于它们分别对应地下介质不同的物性参数，故其剖面图表象各异，在这3个瞬时参数谱之中，瞬时相位谱效果最好，瞬时频率谱次之。从3个瞬时剖面中，可以清楚地分辨位于道号50～125之间采样点数150～200之间的破碎带位置，后经钻探验证。因此，根据不同的地质状况选择合适的剖面图，对信号进行分析会比直接利用原始剖面图要更加清晰、有效，它能使实测信号中异常信息的识别变得更加简单、准确。若综合3个参数的瞬时谱，利用多个参数联合评估、解释，则能达到相互验证，提高解释精度的目的。

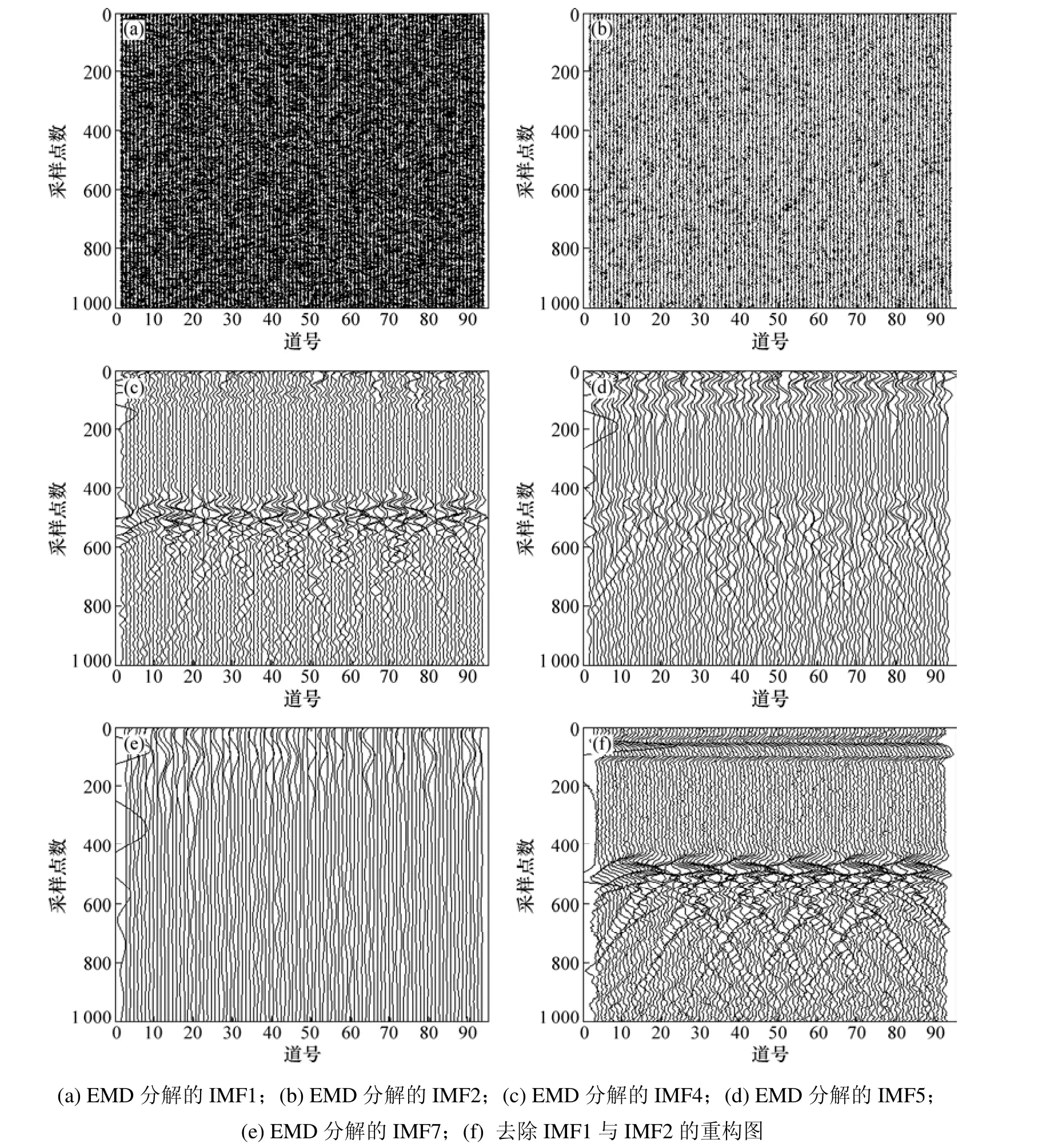
图5 EMD分解得到的IMF1～IMF8及其重构图Fig.5 Maps of IMF1～IMF8 after EMD decomposition and reconstruction

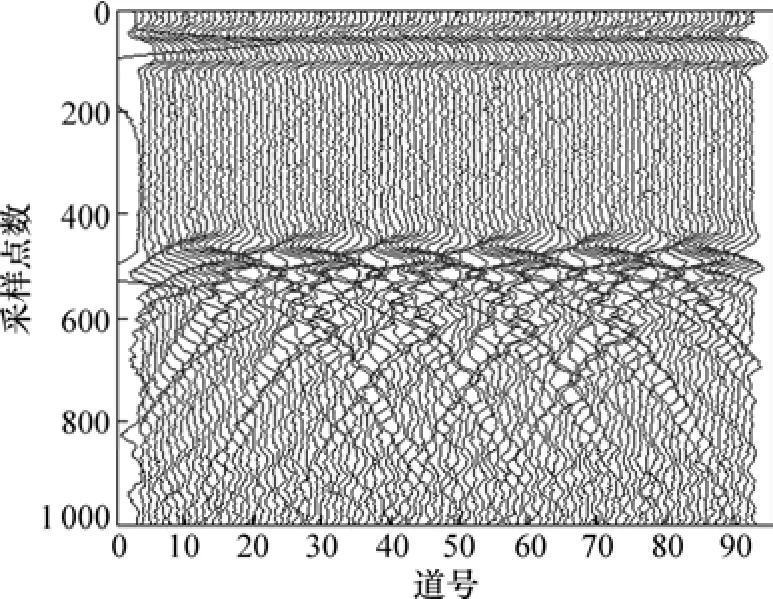
图6 正演资料瞬时振幅剖面Fig.6 Instantaneous amplitude profile of simulated data

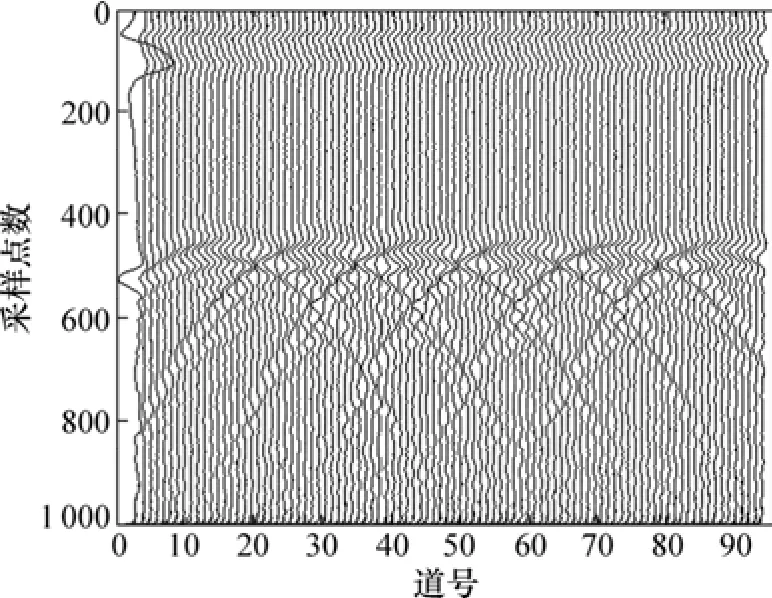
图7 正演资料雷达瞬时相位剖面Fig.7 Instantaneous phase profile of simulated data

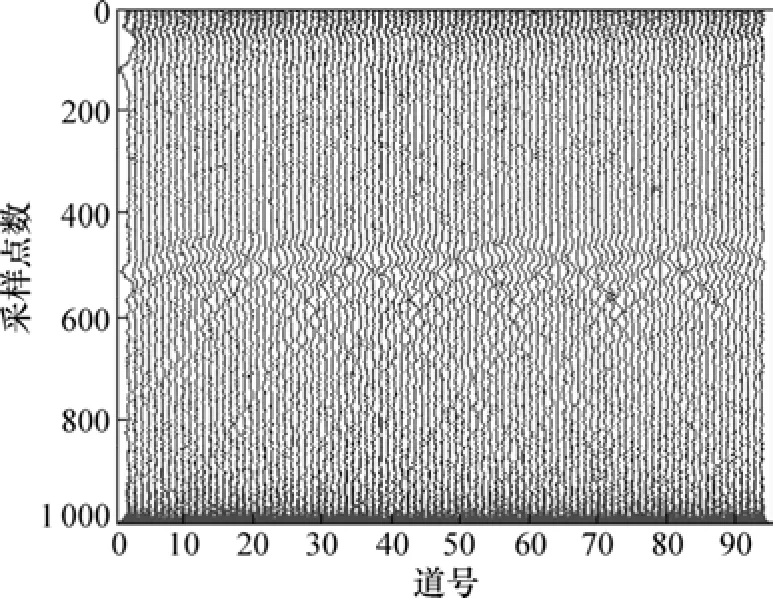
图8 正演资料雷达瞬时频率剖面Fig.8 Instantaneous frequency profile of simulated data

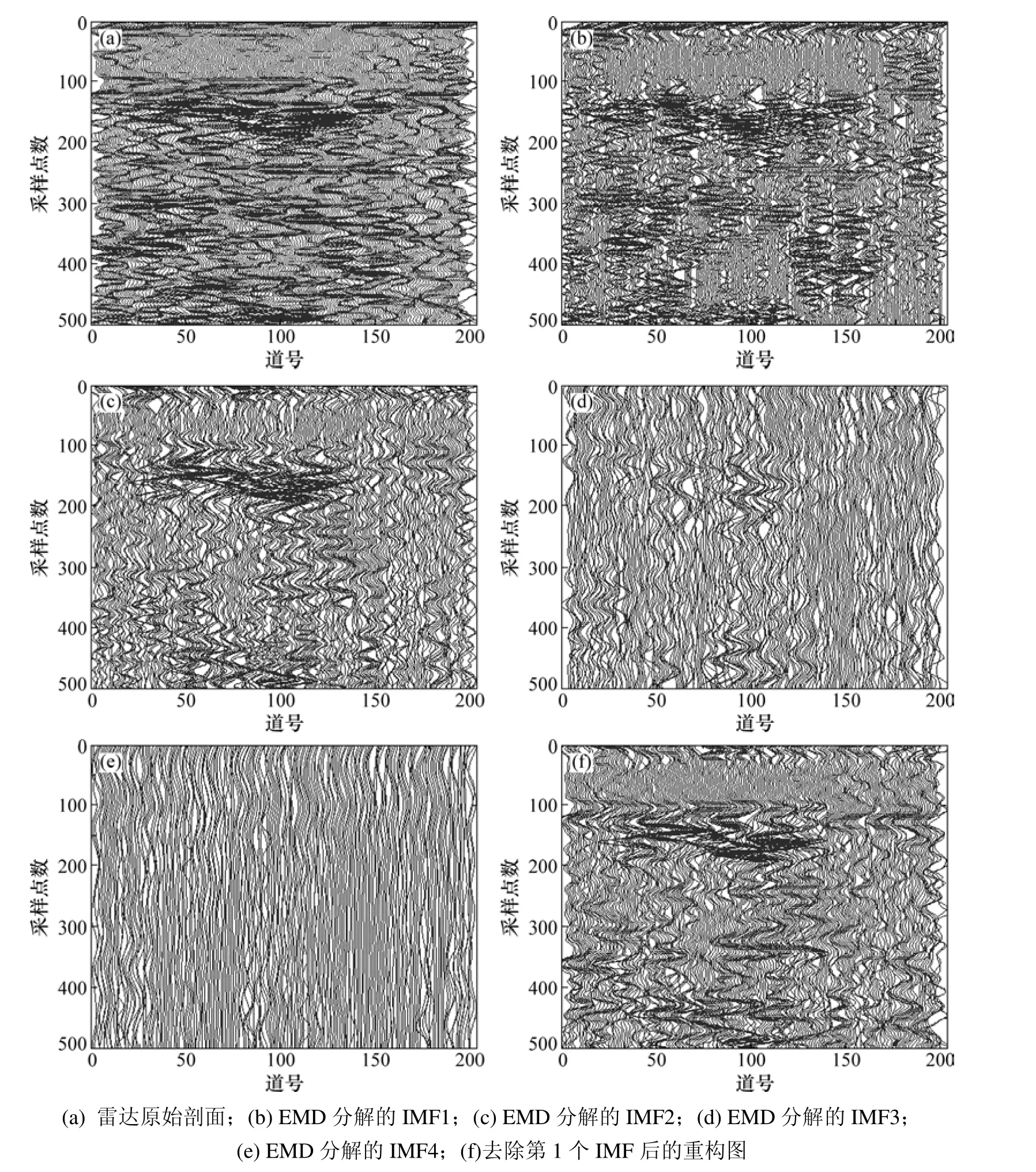
图9 雷达原始剖面与EMD分解得到的IMF1～IMF4及其重构图Fig.9 Original profiles of GPR and IMF1～IMF4 after EMD decomposition and reconstruction profile

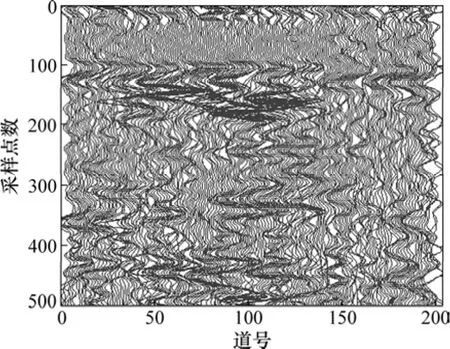
图10 实测资料瞬时振幅剖面Fig.10 Instantaneous amplitude profile of field data

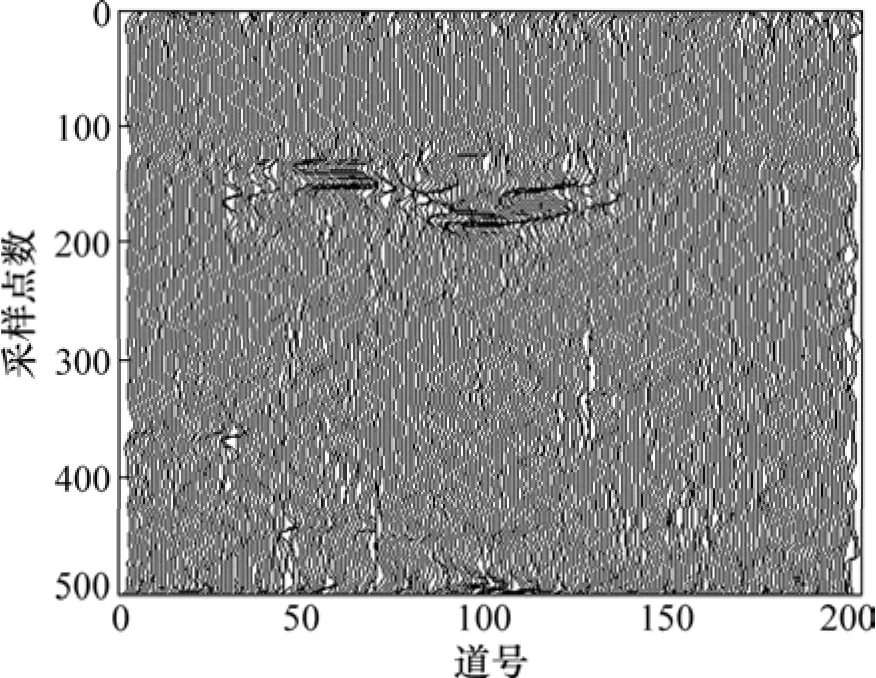
图11 实测资料雷达瞬时相位剖面Fig.11 Instantaneous phase profile of field data

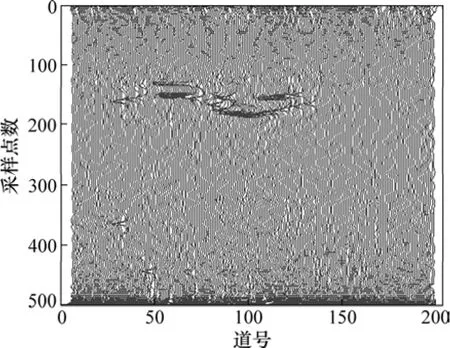
图12 实测资料雷达瞬时频率剖面Fig.12 Instantaneous frequency profile of field data

4 结论

(1) EMD分解的本质是从GPR剖面中从高至低逐步分离出不同频率成分，并通过分屏的方式把各个频率段所对应的异常信息更有效地显示出来，根据不同的数据处理目的，可灵活地对这些IMF雷达剖面图进行处理。EMD分解对于低信噪比雷达数据具有较强的适应性，把 EMD分解应用于含噪的雷达信号，去除含噪的IMF分量再重构GPR剖面，可以较好地实现对低信噪比GPR数据的噪声去除，达到改善GPR信号分析效果、提高信噪比和数据解释精度的目的。

(2) 对 GPR数据先进行 EMD分解，然后结合Hilbert变换和复信号分析求取雷达信号的瞬时特征参数，并用所求得的瞬时振幅、瞬时相位、瞬时频率的三瞬信息特征图与原始信号的剖面图相结合，应用多参数分析方法来表达雷达剖面中蕴含的信息，能够使雷达剖面中的反射界面更加清晰可见，有助于突出雷达剖面中异常体特征，提高GPR数据处理及解释的精度。

[1]曾昭发, 刘四新, 王者江, 等. 探地雷达方法原理及应用[M].北京: 科学出版社, 2006: 159−161.ZENG Zhao-fa, LIU Si-xin, WANG Zhe-jiang, et al. Theory and application of ground penetrating radar[M]. Beijing: Science Press, 2006: 159−161.

[2]翟波, 杨峰, 孙水明, 等. 基于二维滤波的探地雷达数据去噪研究[J]. 南京师范大学学报: 工程技术版, 2007, 7(3): 79−83.ZHAI Bo, YANG Feng, SUN Shui-ming, et al. Research of GPR signal de-noising based on 2-D in ensional filtering[J]. Journal of Nanjing Normal University:Engineering and Technology Edition,2007, 7(3): 79−83.

[3]柳刚, 李术才, 薛翊国, 等. 基于小波变换的雷达低信噪比信号处理技术及应用研究[J]. 工程勘察, 2009(9): 85−90.LIU Gang, LI Shu-cai, XUE Yi-guo, et al. GPR signal processing approach under low signal to noise ratio based on wavelet transforms and its application[J]. Geotechnical Investigation & Surveying, 2009(9): 85−90.

[4]张志禹, 刘亚丽. 基于小波域KL变换的探地雷达信号处理[J].煤田地质与勘探, 2007, 35(2): 70−72.ZHANG Zhi-yu, LIU Ya-li. Signal processing of ground penetrating radar based on KL transforms in wavelet domain[J].Coal Geology & Explorations, 2007, 35(2): 70−72.

[5]吴宝杰, 杨桦, 张伟光. 探地雷达数据的 S变换时频分析[J].上海地质, 2008, 107(3): 13−15, 19.WU Bao-jie, YANG Hua, ZHANG Wei-Guang. S-transform time-frequency analysis of GPR data[J]. Shanghai Geology,2008, 107(3): 13−15, 19.

[6]吴健生, 张昊. 拉东变换在探地雷达资料处理中的应用[J].同济大学学报: 自然科学版, 2005, 33(9): 1270−1273.WU Jian-sheng, ZHANG Hao. Application of radon transform in ground penetrating radar data processing[J]. Journal of Tongji University :Natural Science, 2005, 33(9): 1270−1273.

[7]Huang N E, Shen Z, Long S R, et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationarity time series analysis[J]. Proceedings of the Royal Society London: Series A, 1998, 454: 903−995.

[8]Huang N E, Wu M C, Long S R, et al. A confidence limit for the empirical mode decomposition and the Hilbert spectral analysis[J]. Proceedings of the Royal Society London: Series A,2003, 31: 417−457.

[9]熊学军, 郭炳火, 胡筱敏, 等. EMD方法和Hilbert谱分析法的应用与探讨[J]. 黄渤海海洋, 2002, 20(2): 12−21.XIONG Xue-jun, GUO Bing-huo, HU Xiao-min, et al. The application and research of EMD and Hilbert[J]. Jounal of Oceanography of HuangHai & BoHai Seas, 2002, 20(2): 12−21.

[10]蔡剑华, 王先春. 基于经验模态分解的近红外光谱预处理方法[J]. 光学学报, 2010, 30(1): 267−271.CAI Jian-hua, WANG Xian-chun. Near-Infrared spectrum pretreatment based on empirical mode decomposition[J]. Acta Optica Sinica, 2010, 30(1): 267−271.

[11]皮红梅, 刘财, 王典. 利用 Hilbert-Huang变换提取地震信号瞬时参数[J]. 石油地球物理勘探, 2007, 42(4): 418−424.PI Hong-mei, LIU Cai, WANG Dian. Using Hilbert-Huang transform to pick up instantaneous parameters of seismic signal[J]. Oil Geophysical Prospecting, 2007, 42(4): 418−424.

[12]Flandrin P, Rilling G, Goncalves P. Empirical mode decomposition as a filter bank[J]. Singnal Processing Letters,IEEE, 2004, 11(2): 112−114.

[13]Wu Z, Huang N E. A study of the characteristics of white noise using the empirical mode decomposition method[J]. Proceedings of the Royal Society London: Series A, 2004, 460: 1597−1611.

[14]Damerval C, Meignen S, Perrier V. A fast algorithm for bidimensional EMD[J]. Signal Processing Letters, IEEE, 2005,12(10): 701−704.

[15]汤井田, 化希瑞, 曹哲民, 等. Hilbert-Huang变换与大地电磁噪声压制[J]. 地球物理学报, 2008, 51(2): 603−610.TANG Jing-tian, HUA Xi-rui, CAO Zhe-min, et al.Hilbert-Huang transformation and noise suppression of magnetotelluric sounding data[J]. Chinese Journal of Geophysics,2008, 51(2): 603−610.

[16]段生全, 贺振华, 黄德济. HHT方法及其在地震信号处理中的应用[J]. 成都理工大学学报: 自然科学版, 2005, 32(4):396−400.DUAN Sheng-quan, HE Zhen-hua , HUANG De-ji. Application of the Hilbert-Huang transform to the analysis of seismic signal[J]. Journal of Chengdu University of Technology: Science& Technology Edition, 2005, 32(4): 396−400.

[17]余志雄, 薛桂玉, 周创兵. 复信号分析技术及其在地质雷达数字处理中的应用[J]. 岩石力学与工程学报, 2005, 24(5):798−802.YU Zhi-Xiong, XUE Gui-yu, ZHOU Chuang-bin. The application of complex signals in GPR[J]. The Jurnal of Rock Mechanic and Engineering, 2005, 24(5): 798−802.

[18]谢雄耀, 万明浩. 复信号分析技术在地质雷达信号处理中的应用[J]. 物探化探计算技术, 2000, 22(2): 108−112.XIE Xiong-yao, WAN Ming-Hao. The application of complex signal in treatment of signal of GPR[J]. Geophysical Exploration and Chemical Exploration, 2000, 22(2): 108−112.

[19]汤井田, 蔡剑华, 任政勇, 等. Hilbert-Huang变换与大地电磁信号的时频分析[J]. 中南大学学报: 自然科学版, 2009, 40(5):1439−1405.TANG Jing-tian, CAI Jian-hua, REN Zheng-yong.Hilbert-Huang transform and time-frequency analysis of magnetotelluric signal[J]. Journal of Central South University of Technology: Science & Technology, 2009, 40(5): 1439−1405.

[20]肖兵, 鲍光淑, 赵秋梅, 等. 探地雷达复信号分析及改进[J].中南工业大学学报: 自然科学版, 1997, 28(1): 1−3.XIAO Bin, BAO Guang-shu, ZHAO Qiu-mei, et al. The improvement in complex signal of GPR[J]. Journal of Central South University Technology: Natural Science, 1997, 28(1): 1−3.

[21]杨秋芬. 基于EMD分解的探地雷达信号瞬时频率分析[J]. 煤田地质与勘探, 2009, 37(4): 64−67.YANG Qiu-fen. The instantaneous frequency analysis of GPR data using empirical mode decomposition[J]. Coal Geology &Exploration, 2009, 37(4): 64−67.