基于灰色关联支持向量机的地表沉降预测

谭鹏，曹平

(中南大学 资源与安全工程学院，湖南 长沙，410083)

隧道的地表沉降量与众多随机性、不确定性因素存在着复杂的非线性关系，很难用一种确定的关系进行确定表达。如何用已经监测到的工程参数进行建模，并对沉降的未来演化规律、发展趋势等进行预测，在工程上具有十分重要的意义[1]。目前主要方法是传统分析方法、智能岩石力学的神经网络方法和灰色理论。传统分析方法是利用观测的历史沉降位移建立预测的统计模型，但是，这种统计模型一般当因变量和自变量之间是线性关系或一些简单的函数关系时才使用，同时，当数据太少时不具有统计意义。智能岩石力学的神经网络方法也是基于大样本的一种学习方法。灰色理论在部分信息未知的小样本、贫信息的系统预测中是一种非常有效的方法[2]，但近年来的研究表明[3−5]，该方法由于本身存在一些理论缺陷，使得预测结果出现较大误差。在此，本文作者基于对岩石力学的研究思路[3−10]，将灰色关联理论与基于统计学习理论发展的新学习方法支持向量机结合起来，将灰色理论中的灰色关联分析应用到支持向量机模型中，充分应用支持向量机对复杂的非线性数据的预测能力[11]，建立灰色关联支持向量机预测模型，以便为隧道地表沉降提供一种预测新途径。

1 灰色关联SVM预测模型

1.1 灰色关联分析

灰色关联分析[2](Grey relational analysis，GRA)的目的是定量地反映出系统与各影响因素的关联度，进而从一个系统的众多子因子中挑选出主因子。其方法是将系统中的因变因子所对应的统计数据转化为几何曲线，灰色关联分析认为曲线几何形状越接近，则关联程度就越大，该曲线所对应的因子即为主导此工程系统发展态势的主要因子。灰色关联计算步骤如下。

(1) 设系统的特征序列为：

被比较序列为：

(2) 由于系统的众多影响因子具有不同的量纲，在数量级上存在较大的差异，因此，为了尽量减少计算和分析过程中的误差，对原始数据列采用均值化法或初值化法加以处理。

(3) 求解参考数列与被比较数列绝对差的最大值和最小值。灰色关联度系数ε(k)按如下公式计算：

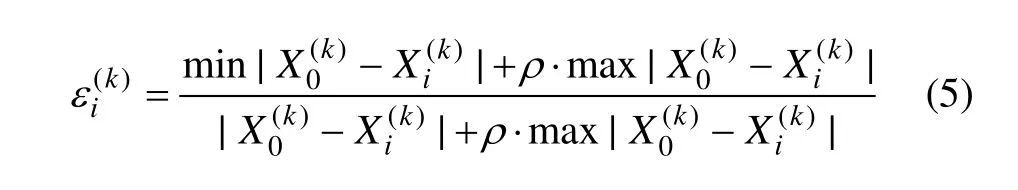
(4) 求解关联度，并按照从大到小的顺序依次排列关联度，关联度最大的为主要因子。

1.2 支持向量机理论

支持向量机[11](Support vector machine，SVM)是Vapink等根据统计学习理论中结构风险最小化原则提出的，具有很好的泛化性能。SVM既有严格的理论基础，又能较好地解决小样本非线性高维数和局部极小点等实际问题。用它建模不必知道因变量和自变量之间的关系，利用支持向量机空间中构造的最优决策函数，通过事先选择的非线性映射将输入样本向量因子映射到高维特征空间，并在这个高维空间中，寻求获得因变量和自变量之间非常复杂的非线性映射关系[4−5]，其核心思想就是学习机器要与有限的训练样本相适应。基本过程如图1所示。

对于支持向量机函数拟合问题就是用函数f(x)=w·x+b 拟合数据{Xi，Yi}(i=1，2，…，n)，Xi∈Rn，Y∈R。数据样本为n维向量的问题，按照支持向量机理论拟合函数为：

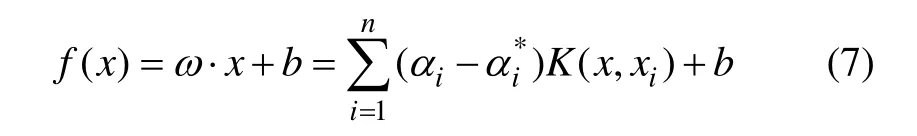
式中αi，αi*和b通过解下面的二次优化问题获得：

此时，通常αi和只有一小部分不为0，即为模型中的支持向量。式中：C为1个正常数；ε为惩罚因子，表示对超出误差ε的样本的惩罚程度；K(xi，xj)为核函数；对于非线性问题，若在原始空间中的得不到满意的结果，则可以通过非线性变换转化为某个高维空间中的线性问题。变换可能比较复杂，SVM通过引入核函数进行变换从而巧妙地解决了这一问题。核函数是通过非线性变换Φ把输入空间Rn中的数据矢量x映射到1个高维特征空间F中。

图1 支持向量机结构示意图Fig.1 Sketch of support vector mechine

高维计算问题目前常用的核函数主要有以下几种。

(1) 多项式函数：

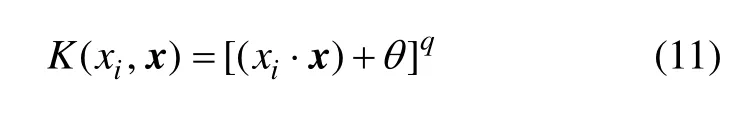
(2) RBF核函数：

(3) Sigmoid核函数：

关于式(13)，(14)和(15)对应的二次优化问题，目前已有多种方法求解，在支持向量机问题中常用的方法有内点算法、SMO方法、分解方法等。

1.3 建模结构及参数的选择

隧道的地表沉降受众多复杂因素的影响，尤其是对样本量和样本有无规律都同样适用的特点，为解决系统问题提供了可能性。掘进隧道引起的地表沉降系统是1个典型的灰色系统，影响最大沉降量H和沉降槽系数i的因子众多，因此，可以根据灰色关联分析原理，确定影响沉降的主要因子，消除无关因子的干扰，以此作为对支持向量机(SVM)输入数据的前期处理，从而提高模型的预测能力。

本文是用模拟退火算法[10−11]来搜索 SVM 的最优的核函数 K(xi，xj)和参数 c。GR-SVM 预测模型结构图见图2。首先，初始化参数设置，随机产生一组初始SVM参数，用给定的样本训练这一组由SVM参数所对应的模型；然后，用获得的 SVM 模型对给定的检验样本进行预测，以检验样本中最大预测误差作为适应值。通过模拟退火算法搜索迭代直到找到满意的SVM 参数为止[10−11]。

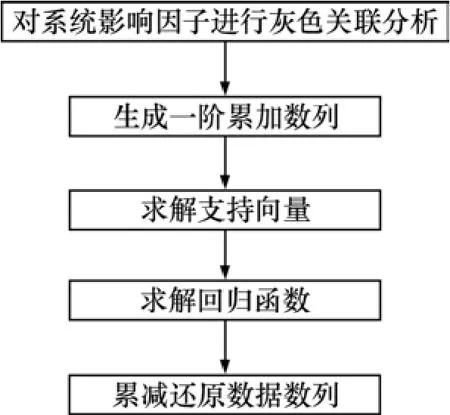
图2 GR-SVM预测模型结构图Fig.2 Sketch of GR-SVM’s prediction model

灰色关联支持向量机模型首先用灰色关联方法获取主因子，然后，利用灰色预测方法对原始序列进行一次累加，生成一阶累加序列。并利用支持向量机拟合非线性数据能力的优势对生成序列建立预测模型，最后将预测结果进行累减还原得到预测值。

2 实例分析

本文依据文献[12]中的实测资料建立GR-SVM预测模型。主要以3个场地的盾构工程为对象进行分析，包括上海地铁二号线龙东路到中央公园盾构工程、广州地铁二号线越秀公园道三元里盾构工程、南京地铁盾构工程。采用GR-SVM所得smax和i的预测值与实测值对比分别见表1和表2。地表沉降的GR-SVM训样品参数见表3和表4，其中：c为土层黏结力；H为隧道埋深；n为土的固结度；φ为内摩擦角；D为隧道直径；F为盾构推力压力；Es为割线弹模；P为注浆压力值；v为盾构机推进速度。

选取26个施工监测点的实例，对地面最大沉降量Smax和沉降槽宽度系数i分别建立GR-SVM预测模型。随机地选取20个监测点作为预测模型的学习样本(见表3)，其余的6个样本实例(表4)用于测试模型的预测能力。用学习样本完成对GR-SVM模型的训练，建立预测模型对剩余的6个样本进行预测。

表1 smax预测值与实际值对比(GR-SVM)Table 1 Comparison between predicted and measured data of smax

表2 i预测值与实际值对比(GR-SVM)Table 2 Comparison between predicted and measured data of i

表3 地表沉降的GR-SVM训练样本参数Table 3 Learning samples for surface settlement

表4 地表沉降的GR-SVM训练样本Table 4 Prediction samples for surface settlement

建立灰色关联分析模型选取主要影响因子。对特征序列和比较序列进行归一化处理，并根据式(1)～(6)进行系统的特征序列和系统影响因素灰色关联度分析，结果如表3所示。

3 结果分析

从表1和表2可知：smax预测值的最大绝对误差的绝对值为3.780 mm，最大相对误差为17.8%；i预测值最大绝对误差的绝对值为 0.385 mm，最大相对误差是6.55%；总体上具有较高的精度。

为了比较GR-SVM方法的预测精度，本文利用表3中的学习样本选取 SVM 方法建立隧道地表沉降的预测模型。预测样本通过GR-SVM和SVM 2种模型所得的预测误差对比结果如表5所示。算法模型的精确度在很大程度上取决于所采用算法性能。为了便于采用量化的方法表示计算模型的性能，本文引入指标判识率(True accept rate，TAR)，即与实测值相符的预测值加以接收的正确概率。根据预测结果发现GR-SVM 的判识率达到 95%，SVM 的判识率只达70%，2种模型均能表达地表沉降的非线性关系。但由表 5比较 2种模型的预测误差可以看出：基于GR-SVM 的隧道地表沉降的非线性组合预测精度更高，优于单一的 SVM 预测模型预测精度。表明灰色关联支持向量机模型在合适的核函数等支持向量机参数下具有较高的预测精度。

在以上 2种模型的建立过程中均发现核函数K(xi，xj)和参数c对预测结果的影较大，因此，寻找一种合适的算法来搜索SVM的最优的核函数K(xi,xj)和参数 c，可以克服试算的低效率和盲目性。将模拟退火算法和支持向量机相结合，用模拟退火算法来搜索支持向量机参数[10−11]。smax和i的预测值与实测值对比结果分别见图3和图4。

图3 smax预测值与实际值对比Fig.3 Comparison between predicted and measured data of smax

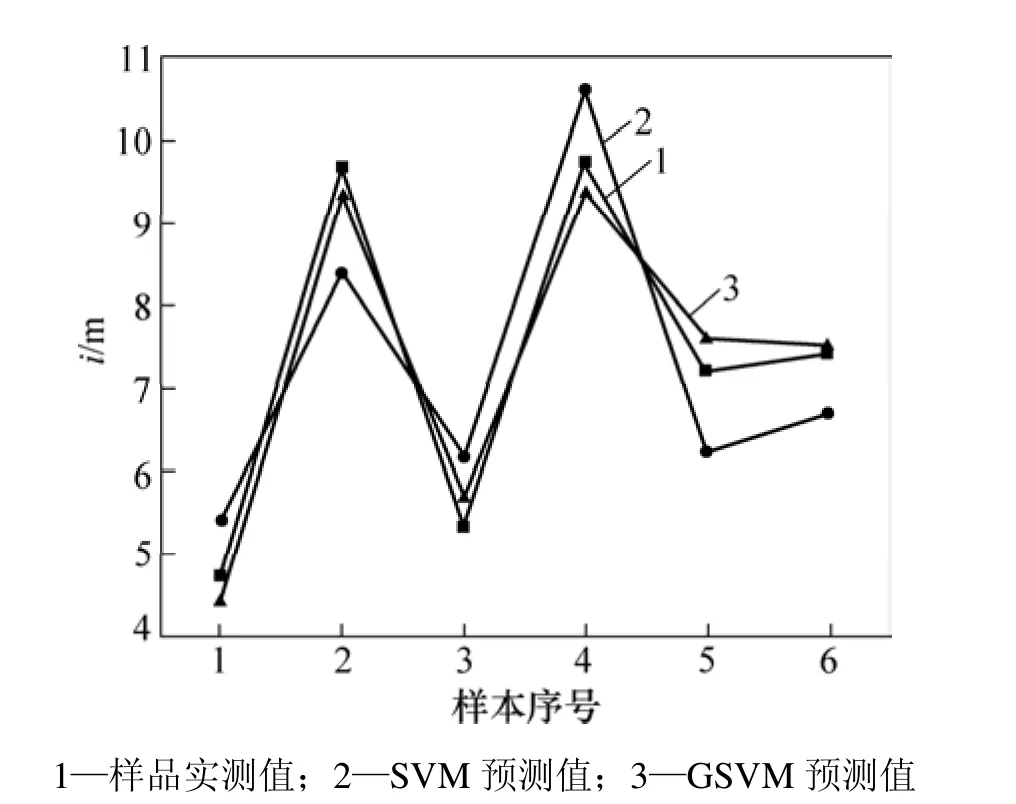
图4 i预测值与实际值对比Fig.4 Comparison between predicted and measured data of i

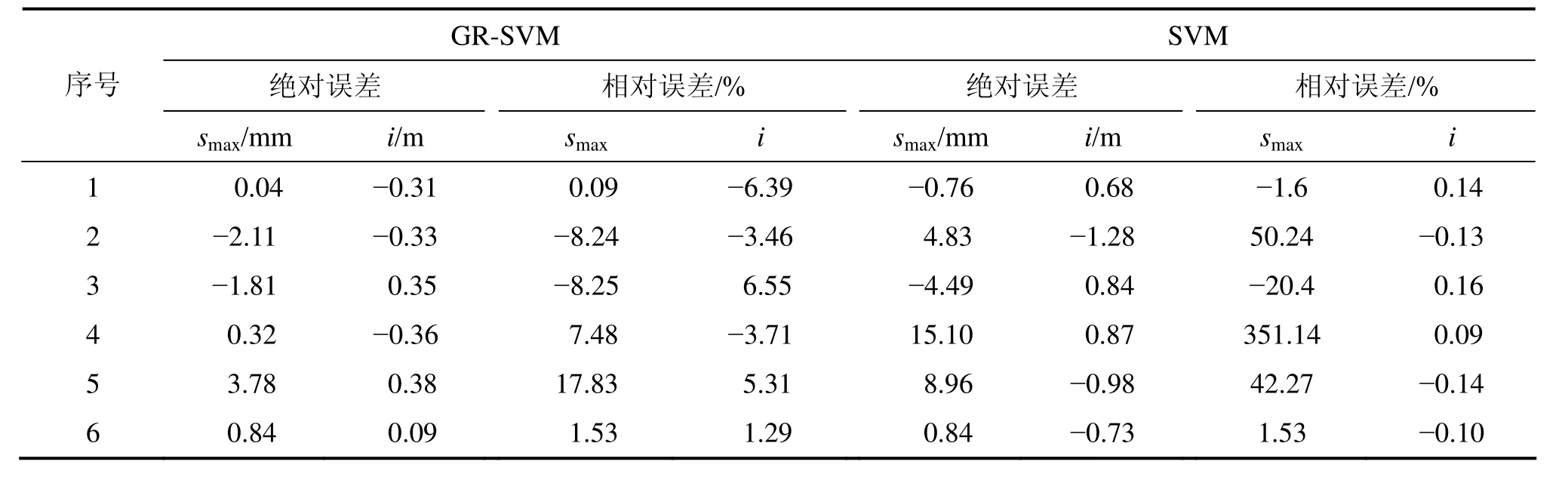
表5 测试样本误差Table 5 Error of test samples of surface settlement

4 结论

(1) 灰色关联支持向量机的分析方法是对学习样本数据和预测样本数据进行关联分析处理，并充分利用了SVM在处理高维数、非线性问题的优良特性。

(2) 用GR-SVM建立起岩土体力学参数与变形之间复杂的非线性映射关系，能够较好地拟合预测复杂的地表沉降系统。该模型比较全面地反映了系统的变化特征，提高了对未来状态分析的效率和预测精度。

[1]冯夏庭. 智能岩石力学导论[M].北京: 科学出版社, 2000:111−116.FENG Xia-ting. Introduce of intelligent rock mechanics[M].Beijing: Science Press, 2000: 111−116.

[2]陈新民, 罗国煜. 基于经验的边坡稳定性灰色系统分析与评价[J]. 岩土工程学报, 1999, 21(5): 638−641.CHEN Xin-min, LUO Guo-yu. Grey system analysis and evaluation of slop stability based on experience[J]. Chinese Journal of Rock Mechanics an Engineering, 1999, 21(5):638−641.

[3]林耀进, 周忠眉, 吴顺祥. 集成灰色支持向量机预测模型研究与应用[J]. 计算机应用, 2009, 29(12): 3287−3289.LIN Yao-jin, ZHOU Zhong-mei, WU Shun-xiang. Research and application of integrated grey support vector machine model[J].Journal of Computer Applications, 2009, 29(12): 3287−3289.

[4]赵洪波, 冯夏庭. 非线性位移时间序列预测的进化−支持向量机方法及应用[J]. 岩土工程学报, 2003, 25(4): 468−471.ZHAO Hong-bo, FENG Xia-ting. Study and application of genetic-support vector machine for nonlinear displacement time series forecasting[J]. Chinese Journal of Geotechnical Engineering, 2003, 25(4): 468−471.

[5]赵洪波, 冯夏庭. 位移反分析的进化支持向量机研究[J]. 岩石力学与工程学报, 2003, 22(10): 631−633.ZHAO Hong-bo, FENG Xia-ting. Study of geneticsupport vector machine in displacement back analysis[J]. Chinese Journal of Rock Mechanics and Engineering, 2003, 22(10): 631−633.

[6]景海河, 叶欣. 基于支持向量机的矿区开采沉降的预测[J].黑龙江科技学院学报, 2008, 18(4): 250−252.JING Hai-he, YE Xin. Subsidence prediction of diggings based on support vector machine[J]. Journal of Heilongjiang Institute of Science & Technology, 2008, 18(4): 250−252.

[7]徐传华, 任青文, 周庆华. 基于支持向量机和模拟退火算法的位移反分析[J]. 岩石力学与工程学报, 2005, 24(22):4134−4138.XUN Chuan-hua, REN Qing-wen, ZHOU Qing-hua.Displacement back analysis based on support vector machine and simulated annealing[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(22): 4134−4138.

[8]Kirkpatrick S, Gelatt C D, Veccki M R. Optimization by simulated annealing[J]. Science, 1983, 220: 67l−680.

[9]赵洪波, 冯夏庭. 支持向量机函数拟合的边坡稳定性估计[J].岩石力学与工程学报, 2003, 22(2): 241−245.ZHAO Hong-bo, FENG Xia-ting. Application of support vector machines function regression in the evolution stability of slope[J]. Chinese Journal of Rock Mechanics and Engineering,2003, 22(2): 241−245.

[10]赵洪波. 支持向量机在隧道围岩变形预测中的应用[J]. 岩石力学与工程学报, 2005, 24(4): 649−652.ZHAO Hong-bo. Predict the surrounding deformations of tunnel using support vector machine[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(4): 649−652.

[11]Cristianini N, Taylor S T. 支持向量机导论[M]. 李国正, 王猛,译. 北京: 电子工业出版社, 2004: 81−129.Cristianini N, Taylor S T. An introduction to support vector machines and other kernel-based learning methods[M]. LI Guo-zheng, WANG Meng, transl. Beijing: Electronics Industry Press, 2004: 81−129.

[12]李守巨, 刘应曦, 孙伟. 智能计算与参数反演[M]. 北京:科学出版社, 2008: 145−274.LI Shou-ju, LIU Ying-xi, SUN Wei. Intelligence computation and parameter identification[M]. Beijing: Science Press, 2008:145−274.