基于实测边界线的地下巷道三维建模方法
谭正华 ,王李管,熊书敏,刘任任
(1. 湘潭大学 湖南省高等学校智能制造重点实验室,湖南 湘潭,411105;2. 中南大学 数字矿山研究中心,湖南 长沙,410083)
巷道系统是矿山三维虚拟场景的重要组成部分,是构建数字矿山的基础。已有的三维巷道实体建模研究依据其数据来源可分为两大类:基于中心线(或导线)的巷道实体三维建模和基于实测底板边界线的巷道实体三维建模。基于中心线的巷道建模已发展一些较成熟的算法[1−4],但多数金属矿山存在大量实测的巷道底板边界数据,这些数据形象地描述了各中段巷道底板宽度信息和巷道间的贯通情况。因此,基于实测底板边界线的巷道三维建模更接近实际情况,建模相对复杂且更具一般性。孙卡等[5]提出了采用约束三角剖分的方法生成巷道模型的上下底盘面,利用两段成面法生成巷道模型的侧面,最后将这些面组合成巷道模型。但该方法难以解决常见的圆弧拱、三心拱等断面的巷道建模问题。分层建模方法[1]是生成连通巷道实体的有效方法,可用于群体工程连通精细建模。本文借鉴文献[1]中分层轮廓线的概念,设计一种基于实测底板边界线和断面参数,构造巷道实体的分层轮廓线,生成地下巷道三维实体模型的方法。
1 算法原理及流程
实测的边界线将其所在的平面划分为1个或多个封闭区域(内含孔洞)。本文采用区域树[6]表达边界线所划分的区域,1个区域对应1个区域树。树的层次结构表达了边界线之间的空间拓扑关系;然后采用约束三角剖分的方法将各区域网格三角化,同时提取三角形中表示“出口”和断面底板的边;根据断面生成断面轮廓线,然后均匀离散化各断面轮廓线,生成表示实体巷道的特征点;根据区域树表示的边界拓扑关系,分层提取特征点,生成分层轮廓线;最后,对相邻轮廓线采用“基于轮廓线的三维重构”算法和对顶、底轮廓线采用“多边形区域三角化”算法,从而实现巷道体的网格三角化。
基于边界线的巷道建模主要分为2个主要部分:(1) 数据的前期处理。由于矿山实测数据多存在重复点、重复线,而且以DWG和DXF格式保存的数据为二维平面数据,故必须进行删除重复点、重复线操作,同时必须调整边界线的高程。(2) 根据边界线和断面构造三维井巷实体。需要注意的是:构成巷道内外边界线必须闭合。三维巷道建模流程图见图1。
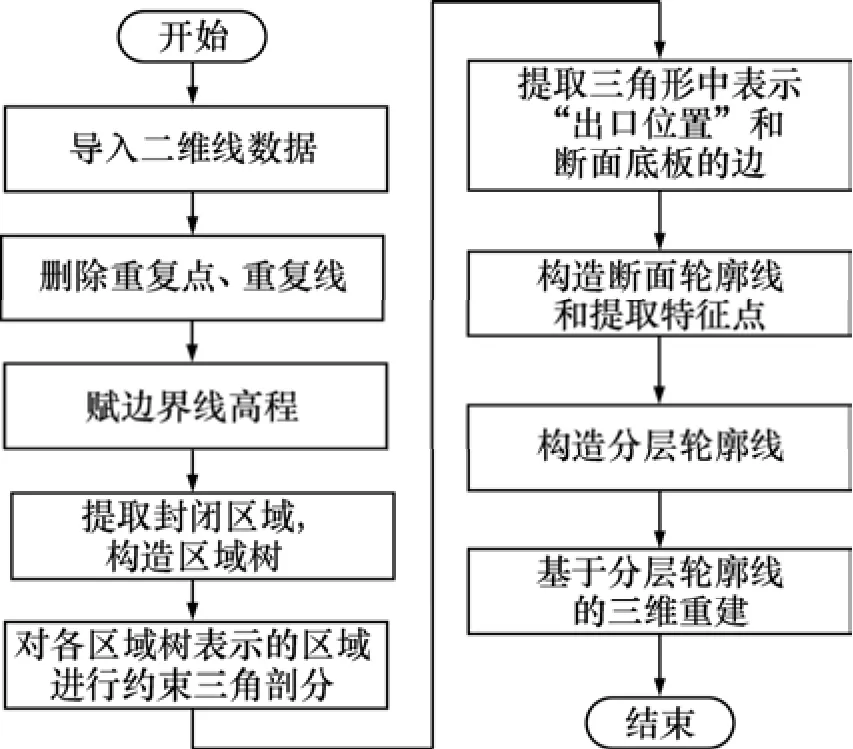
图1 三维巷道建模流程Fig.1 Process of 3D modeling for laneway
2 算法的关键过程
2.1 构造区域树
基本原理是采用树结构来表达边界线划分的区域,区域树具有如下特点:
(1) 1个封闭区域映射1个区域树。
(2) 区域树的结点表示区域的内、外边界(即巷道的底板边界),其根结点表示该区域的最外围边界,子结点表示区域内部的孔、岛边界。
(3) 结点之间的上下层次关系表示边界的包含关系,同层结点表示边界的并列关系。
(4) 边界是有方向性的,并对边界方向作如下规定:区域最外围边界的走向为逆时针方向,内部孔洞边界沿顺时针方向,岛边界沿逆时针方向。
如图2(a)所示,某实测的巷道底板边界线a,b,c,d和e将该中段划分为1个封闭区域,见图2(b);阴影部分表示划分的封闭区域,该区域内含4孔洞,其对应的区域树表示见图2(c)。
区域的提取方法有多种[6−8],其中文献[6]给出了定向极大、极小闭环的概念,通过建立结点−路径网络拓扑结构图,采用内层路径优先查找算法,提取所有定向闭环,最后建立定向极小闭环和定向极大闭环的隶属关系,建立区域树,有效地实现了复杂区域的识别、提取,具有普遍适用性。本文采用文献[6]中的算法提取中段平面的所有复杂区域。

图2 区域和对应的树结构Fig.2 Region and its representation using tree structure
采用区域树形式化表达了巷道底板边界间的空间拓扑关系,为区域的三角化提供了数据来源。
2.2 多边形区域的三角化
多边形的三角剖分就是在不产生新顶点的条件下将平面多边形划分成一系列不相重叠的三角形[9]。多边形三角剖分算法有多种[10−13],其中,毕林等[13]提出的三角化算法适用带洞、岛的任意简单多边形,时间复杂度近似O(n),采用该算法,对巷道底板边界线多边形网格三角化,生成结果局部示意图见图3。
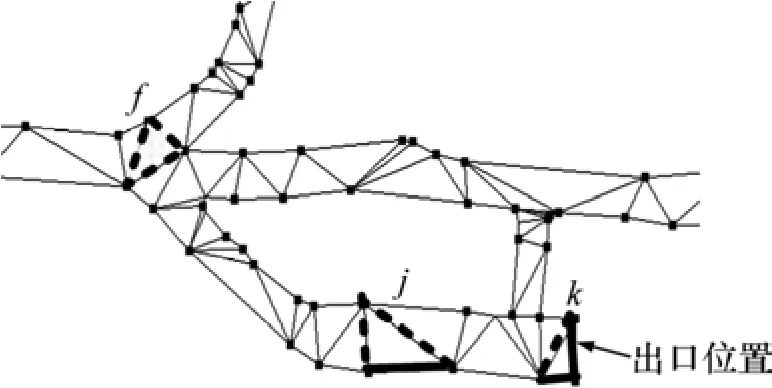
图3 多边形区域三角化示意图Fig.3 Schematic diagram of polygon triangulation
2.3 提取表示“出口”位置和断面底板的边
根据网格三角形和底板边界共边的数目,将三角形分为3类:(1) 不共边的三角形;(2) 共1条边的三角形;(3) 共2条边的三角形。见图3中的三角形f,j和k,三角形中的实粗线部分表示该边和原边界线共边,虚粗线表示不共边。
“出口”位置的边只存在于第3类三角形中。表示“出口”位置的边和其前后的边有明显角度变化,根据这一特征对其进行识别和提取;第1和2类三角形中不与边界重合的边中最短的边作为断面底板的边。
2.4 断面轮廓线和特征点的构造
设计的巷道断面有固定的底边宽度、墙高、拱高,形状比较规则,反映了设计图中垂直于巷道中线处的断面形状和尺寸,见图4。提取的断面底边和巷道中线往往是不垂直的,故需要根据垂直中线处的断面轮廓线,通过投影变换建立断面底板处的断面轮廓线。
以图5为例,当断面形状为三心拱时,构造底板AC处的断面轮廓线算法如下。
步骤 1:构造垂直于巷道中线的直线段 AB。AB的长度表示断面的底宽。根据设计断面中的“拱高/底宽”(一般为1/3,1/4或1/5)确定该处的实际拱高。
步骤 2:根据断面参数中的墙高、巷道底宽和拱高,拟合AB处的断面轮廓线。
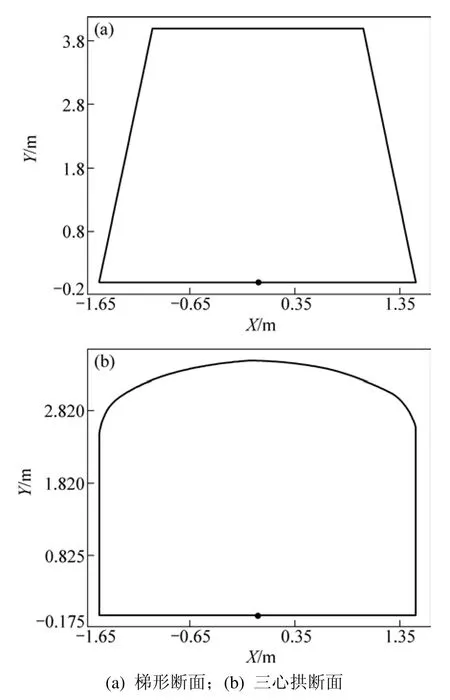
图4 2种常见的巷道断面Fig.4 Two laneway cross-sections
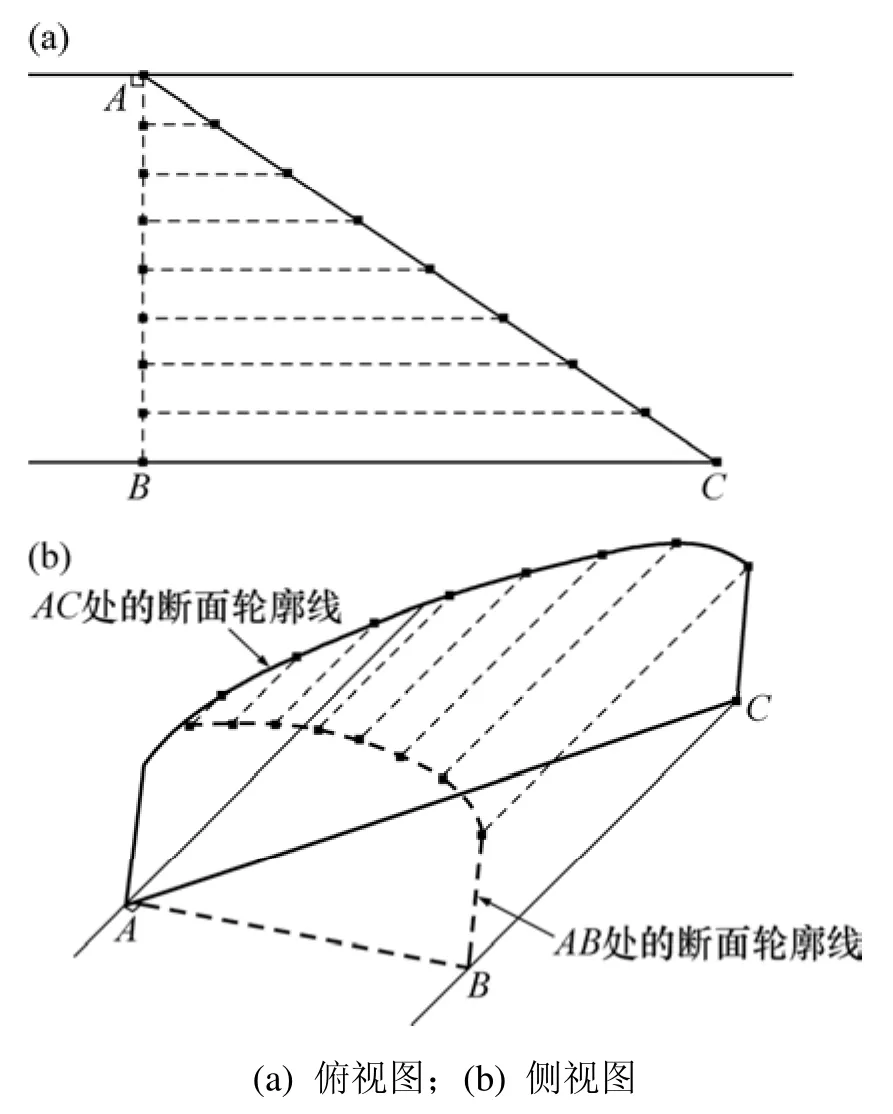
图5 建立断面轮廓线Fig.5 Reconstruct cross-section contour
步骤 3:通过投影变换,建立 AC处的断面轮廓线。
离散化断面轮廓线,获取巷道断面的特征点。以梯形断面和三心拱断面为例(见图6),梯形断面存在2组特征点:(p0−p1)和(p2−p3),三心拱断面有 5组特征点:(p0−p1),(p2−p3),(p4−p5) ,(p6−p7),(p8−p9)。
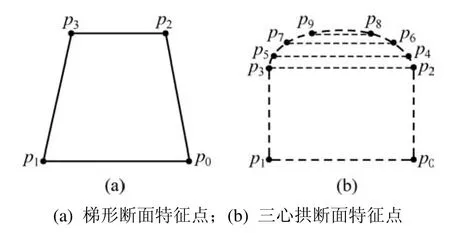
图6 提取断面轮廓线特征点Fig.6 Laneway section data acquiring
2.5 构造巷道实体的分层轮廓线
区域树结构表达了底板边界的空间拓扑关系,通过获取断面轮廓线的特征点,建立巷道实体的分层轮廓线。当断面形状分别为梯形和三心拱时,构造的分层轮廓线示意图见图7。
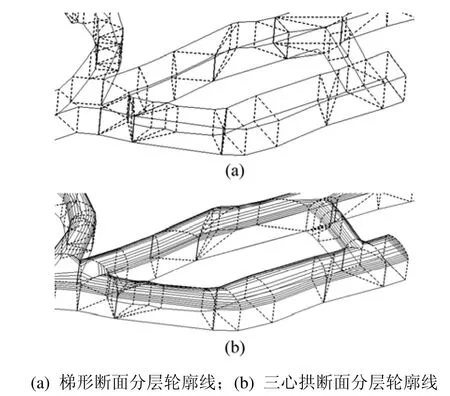
图7 巷道实体的分层轮廓线Fig.7 Hierarchical contours of laneway
2.6 基于分层轮廓线的三维重建
在生成巷道实体分层轮廓线的基础上,巷道实体表面的重建问题转化为基于一组轮廓线重建其三维表面。许多学者在三维重建方面进行了很多研究[14−18]。对于 2条连续的截面轮廓曲线之间的三角划分的问题,周焰等[15]提出了一种利用物体2个截面轮廓曲线
一般有较大的相似性这一事实,首先进行粗略分块,然后在块内进行三角划分,从而实现了一种三维物体表面重建的多尺度算法。文献[16]对文献[15]的方法进行了改进,首先采用一种改进的CSS方法提取轮廓曲线的角点,其次进行角点配对,采用一种新的配对方法,根据曲线间距离设定动态阈值,根据配对情况进行轮廓相似性判断;在相似的轮廓曲线之间根据配对情况进行分块。每个块内部进行的简单的三角划分与文献[14]中的方法一样。由于巷道实体的分层轮廓线之间存在相似性,本文采用文献[16]中方法实现对所有相邻的分层轮廓线网格三角化(见图8)。巷道实体是封闭的,因此,还必须分别对顶、底轮廓线实现多边形的区域三角化。本文采用文献[13]中算法实现了顶、底轮廓线的网格三角化。最后,对所有的三角化网格合并,最终生成封闭的三维巷道实体表面模型。
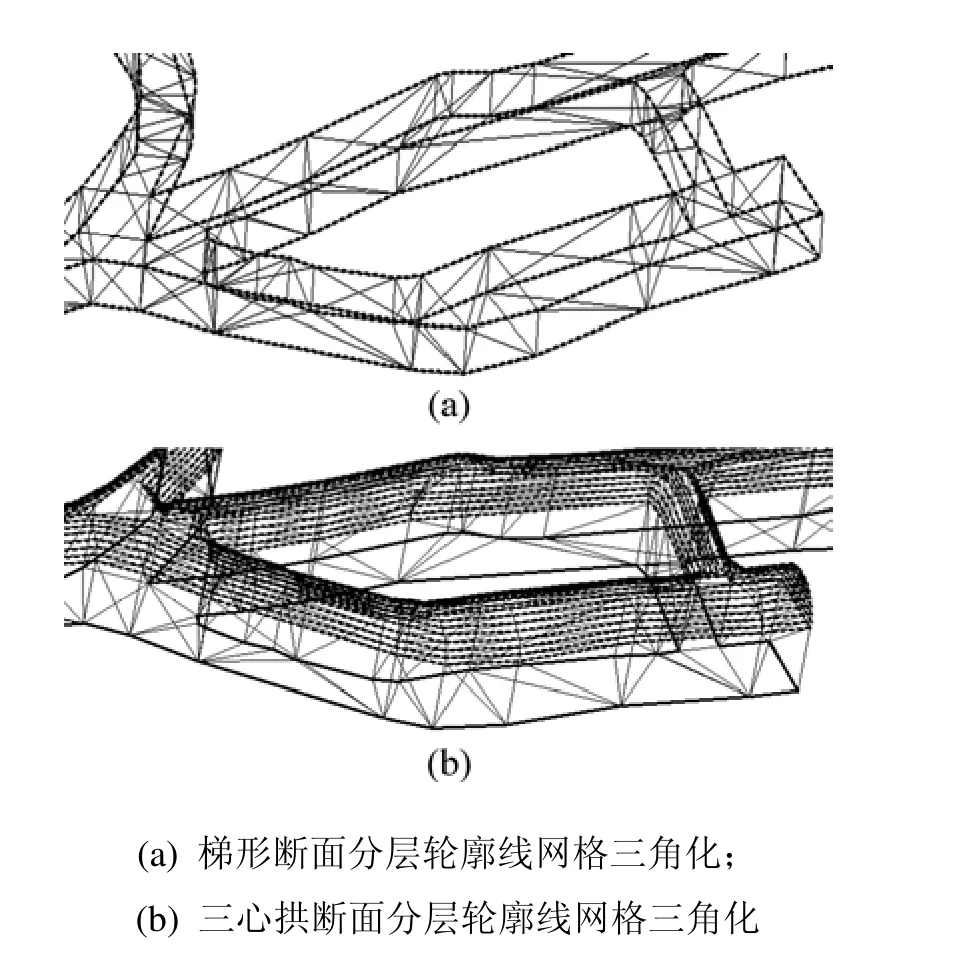
图8 基于分层轮廓线的网格三角化Fig.8 Triangulation based on hierarchical contours
3 算法分析和应用实例
3.1 算法复杂度分析
该算法时间复杂度主要由以下几部分确定:(1)基于边界轮廓线的区域树构造,当存在l个极大闭环和k个极小闭环时,该算法时间复杂度为O(lk)[6];(2)多边形的区域三角化,定义多边形的顶点数目为 n,三角化时间复杂度近似线性,即O(n);(3)网格的生成,包括分层轮廓线的曲面重建[17]和顶、底轮廓线的三角化[13],时间复杂度与顶点数均近似线性。故总的时间复杂度为:O(lk)+O(n)。
3.2 应用实例
通过VC+开发工具和HOOPS可视化工具包实现了该算法,运行环境为Windows 2000操作系统,CPU为Inter Pentium4 3.00 GHz,内存为512 MB。对图3(a)所示底板边界线生成巷道实体(三心拱断面、梯形断面),局部渲染效果见图9。
实验 1:当边界线数为8,13,17,30和42时,分别生成巷道(三心拱断面),耗时如表 1所示,边界数与时间关系如图10所示。
实验 2:对图3(a)中边界线的顶点坐标进行线性插值加密,分别得到顶点个数为678,1 662,3 074,5 419和7 830,生成巷道(三心拱断面)耗时结果如表2所示,其顶点数−时间曲线如图11所示。从图11可见:当边界数一定时,算法耗时与顶点数呈近似线性关系。
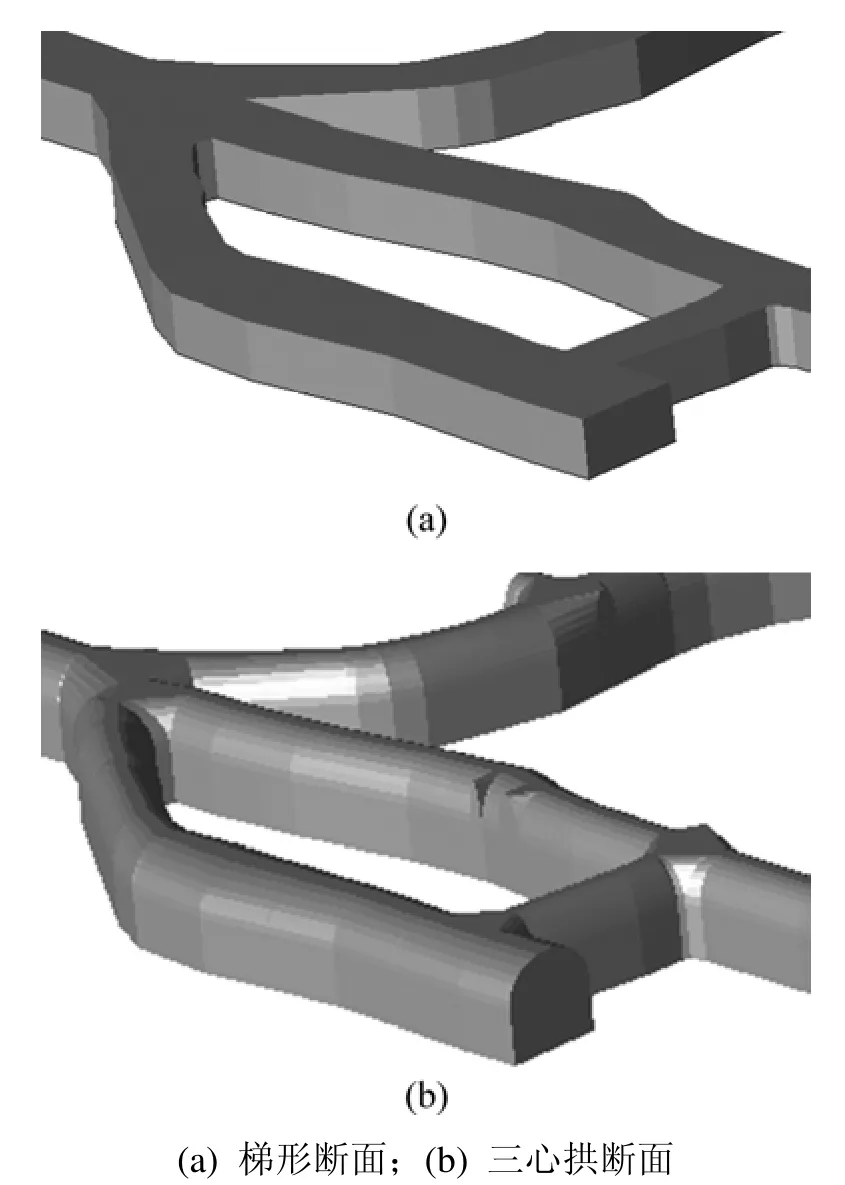
图9 局部渲染效果图Fig.9 3D rendering for laneway model
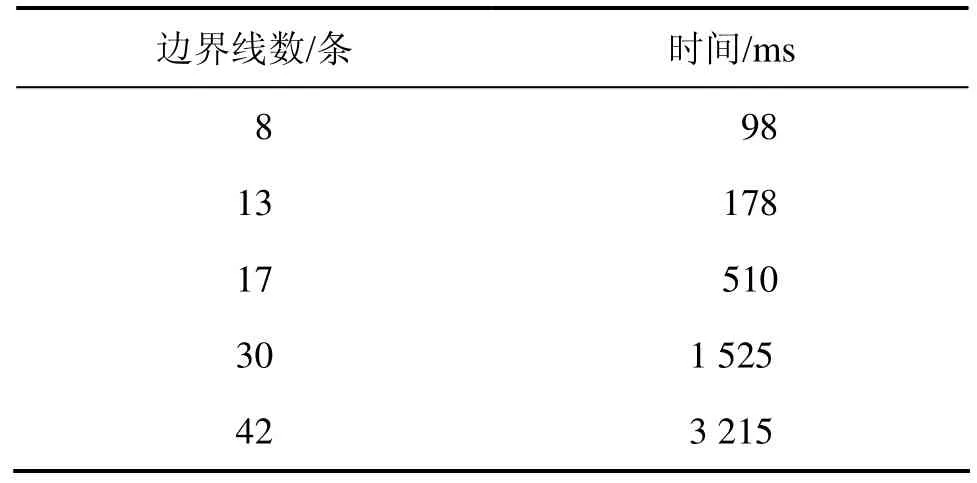
表1 不同边界线数算法耗时Table 1 Consuming times for different numbers of boundary

图10 边界数−时间曲线Fig.10 Time changes with different numbers of boundary

表2 不同顶点个数算法耗时Table 2 Consuming time for different numbers of vertex
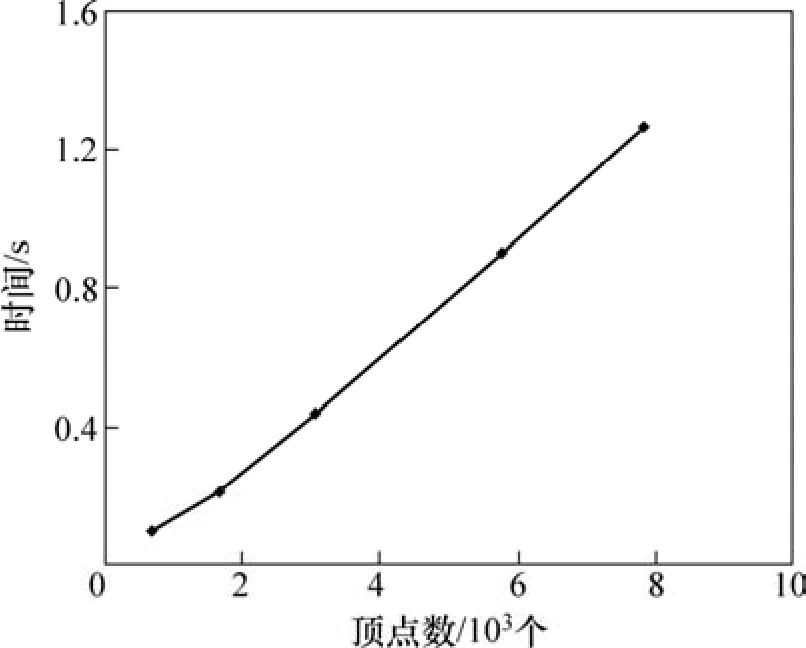
图11 顶点数−时间曲线Fig.11 Time changes with different numbers of vertex
4 结论
提出了一种有效的实测巷道三维建模方法。根据实测巷道底板边界线和断面形状,生成巷道实体的特征点,构造分层轮廓线,采用连线框和网格三角化方法,建立虚拟环境下的三维巷道实体,为下一步虚拟漫游以及采掘量的估算提供数据来源。该方法具有以下优点:
(1) 能有效地解决任意复杂不等宽实测底板边界线和不同断面形状下的巷道实体建模问题。
(2) 当断面形状为三心拱时,建模过程中断面轮廓线的拱高根据工程设计中的拱高和底宽的比(1/3,1/4或1/5)计算得出,要构造更符合实际的巷道三维模型,须进一步探讨和验证。
(3) 边界(多边形)数是影响算法时间复杂度的主要方面,需要进一步降低构造区域树的时间复杂度,如考虑采用 OBB树的碰撞检测算法确定定向闭环之间的隶属关系。
[1]谭正华, 王李管, 毕林, 等. 平面连通巷道三维实体分层建模方法[J]. 武汉大学学报: 信息科学版, 2010, 35(3): 360−363.TAN Zheng-hua, WANG Li-guan, BI Lin. et al. A hierarchicl modeling method for plane connected three-dimensional laneway entity based on media curves[J]. Geomatics and Information Science of Wuhan University, 2010, 35(3):360−363.
[2]徐志强, 杨邦荣, 王李管, 等. 巷道实体的三维建模研究与实现[J]. 计算机工程与应用, 2008, 44(6): 202−205.XU Zhi-qiang, YANG Bang-rong, WANG Li-guan, et al.Laneway entity three-dimensional modeling study and realiza-tion[J]. Computer Engineering and Applications, 2008,44(6): 202−205.
[3]汪云甲, 伏永民. 矿井巷道三维自动建模方法研究[J]. 武汉大学学报: 信息科学版, 2006, 31(12): 1097−1100.WANG Yun-jia, FU Yong-min. On 3D automatic modeling method of mine roadway[J]. Geomatics and Information Science of Wuhan University, 2006, 31(12): 1097−1100.
[4]葛永慧, 王建民. 矿井三维巷道建模方法的研究[J]. 工程勘察, 2006(10): 46−49.GE Yong-hui, WANG Jian-min. 3D modeling method for lane way[J]. Journal of Geotechnical Investigation & Surveying,2006(10): 46−49.
[5]孙卡, 翁正平, 张志庭, 等. 基于带约束三角剖分的三维巷道建模方法[J]. 矿业研究与开发, 2007, 27(5): 64−66.SUN Ka, WENG Zheng-ping, ZHANG Zhi-ting, et al. 3D roadway modeling method based on restrained triangulation[J].Mining Research and Development, 2007, 27(5): 64−65.
[6]谭正华, 王李管, 毕林, 等. 参数曲线集复杂区域的全自动识别算法[J]. 计算机工程, 2010, 36(8): 23−26.TAN Zheng-hua, WANG Li-guan, BI Lin, et al. Automatic identification algorithm for complicated regions of parameterized curve set[J]. Computer Engineering, 2010, 36(8):23−26.
[7]宋怀波, 路长厚, 王富春. 一种新的复杂区域孔洞填充算法[J]. 桂林电子科技大学学报, 2006, 26(6): 451−454.SONG Huai-bo, LU Chang-hou, WANG Fu-chun. A new hole-filling algorithm for complicated connecting regions[J].Journal of Guilin University of Electronic Technology, 2006,26(6): 451−454.
[8]何亚彬, 杨恢先, 代秋芳. 参数曲线集最小闭环提取算法[J].计算机工程与应用, 2005, 41(32): 109−111.HE Ya-bin, YANG Hui-xian, DAI Qiu-fang. An algorithm for picking up minimum closed loops from parameterized curve set[J]. Computer Engineering and Applications, 2005, 41(32):109−111.
[9]马小虎, 潘志庚, 石教英. 基于凹凸顶点判定的简单多边形Delaunay三角剖分[J]. 计算机辅助设计与图形学学报, 1999,11(1): 1−3.MA Xiao-hu, PAN Zhi-geng, SHI Jiao-ying. Delaunay triangulation of simple polygon based on determination of convex concave vertices[J]. Journal of Computer Aided Design& Computer Graphics, 1999, 11(1): 1−3
[10]Gareym R, Johnsond S, Preparata F P, et al. Triangulating a simple polygon[J]. Information Proceeding Letters, 1978, 7(4):175−179.
[11]Seidel R. A simple and fast incremental randomized algorithm forcomputing trapezoidal decompositions and for triangulating polygons[J]. ComputGeom Theory Appl, 1991, 1(1): 51−64.
[12]Chazelle B. Triangulating a simple polygon in linear time[J].Discrete Comp Geom, 1991, 6(5): 485−524.
[13]毕林, 王李管, 陈建宏, 等. 快速多边形区域三角化算法与实现[J]. 计算机应用研究, 2008, 25(10): 3030−3033.BI Lin, WANG Li-guan, CHEN Jian-hong, et al. Fast triangulation algorithm for polygon regions and implementation[J]. Application Research of Computers, 2008,25(10): 3030−3033.
[14]Keppel E. Approximating complex surface interpolation technique for reconstruction 3D objects from serial crosssections[J]. Computer Vision, Graphics, and Image Processing,1989, 48(1): 124−143.
[15]周焰, 李德华, 陈振羽, 等. 三维物体表面三角划分的快速算法[J]. 中国图像图形学报, 2000, 5(9): 764−768.ZHOU Yan, LI De-hua, CHEN Zhen-yu. A fast algorithm of triangulation on 3D surface[J]. Journal of Image and Graphics,2000, 5(9): 764−768
[16]周焰, 李德荣, 徐长勇. 一种基于区域分割的三角划分方法[J]. 武汉大学学报: 信息科学版, 2003, 28(2): 227−231.ZHOU Yan, LI De-rong, XU Chang-yong. A blocking based triangulation of surface between planar contours[J]. Geomatics and Information Science of Wuhan University, 2003, 28(2):227−230.
[17]王强, 马利庄, 鲍虎军. 基于骨架的断层间复杂轮廓线的三角片曲面重构[J]. 计算机学报, 2000, 28(8): 842−846.WANG Qiang, MA Li-zhuang, BAO Hu-jun. Skeleton-based triangular surface reconstruction from complex contour lines[J].Chinese Journal of Computers, 2000, 23(8): 842−846.
[18]Congy G, Parvin B. An algebraic solution to surface recovery from cross-sectional contours[J]. Graphical Models and Image Processing, 1999, 61(3): 222−243.

