基于特征值矩阵的循环平稳检测算法
赵春晖,马 爽,成宝芝
哈尔滨工程大学信息与通信工程学院,哈尔滨,150001
频谱感知技术是认知无线电的关键技术,可确保认知用户不干扰授权用户的正常通信.同时,该技术可靠的感知可为认知用户创造更多占用空闲频谱资源的机会,从而使认知用户实现通信.目前,频谱感知技术一般包括匹配滤波检测[1]、能量检测[2]、循环统计量检测[3]和基于以上3种技术的合作检测[4-5].能量检测方法简单且易于实现,只需测量频域或时域上一段观测空间内接收信号的总能量并判决是否出现授权用户,接收机无需信号的先验知识.然而,能量检测无法区分主用户信号、二级用户信号和干扰.循环平稳检测可在不需任何噪声先验知识的情况下,通过不同的循环频率区分信号,进而在较低信噪比时仍能达到可靠地检测性能[6-7].本研究通过分析循环统计量的计算过程发现经过正交变换,使信号的循环自相关函数向量正交化,信号之间的相关信息未得到充分利用,信息有一定损失.本研究改进了统计量的计算方法,提出基于特征值矩阵的循环平稳检测.
1 循环平稳检测
通信信号具有循环平稳特性,高斯噪声不具有循环平稳特性.根据这一特点,Lunden等[3]提出循环平稳检测方法.文献 [8]提出了多循环频率的循环平稳检测算法.循环自相关函数的估计为

其中,x(t)是接收信号;t是采样时间;M是采样值个数;(*)代表取复共轭.xx(*)(α)是1×2N的循环自相关函数估计向量,由不同循环频率的实部和虚部组成,即
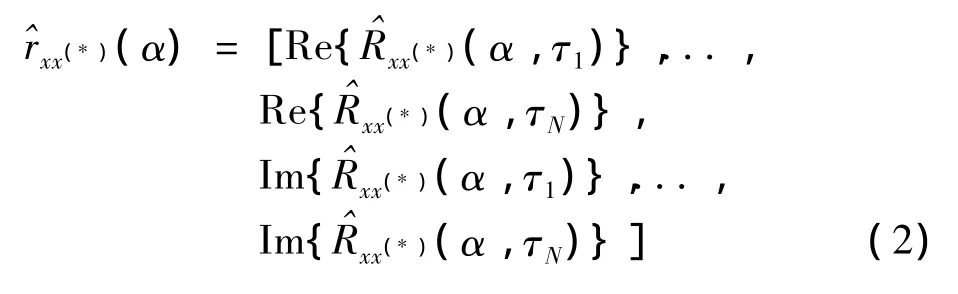
其中,N为延迟个数;Re为取实部;Im为取虚部.为检验在某一频率上是否具有二阶循环平稳特性,假设

其中,rxx(*)是循环自相关函数向量非随机真值;εxx(*)为估计误差,通常假设其服从正态分布.

这里,∑xx(*)是2N×2N的xx(*)协方差矩阵.
根据广义似然比检验,得检验统计量为


2 基于特征值矩阵的循环平稳检测
2.1 统计量分析
由式(3)可知,循环自相关函数的估计存在误差,则式(3)可表示为

其中,ε1为高斯噪声的循环自相关函数;ε2为信号与噪声的交叉项;r为信号的循环自相关函数真值.
理论上,由于高斯噪声是平稳随机过程,当循环频率α≠0时,ε1应为0.又因为信号与噪声独立,因此ε2也为0.实际中,由于信号长度有限,ε1和ε2并不为0.因此,估计误差将会影响统计量的计算.

此时,Λ =diag(λ1,λ2,…,λ2N).其中,P 是由对称矩阵xx(*)的特征向量组成的正交矩阵;Λ是由2N个xx(*)的特征值组成的对角阵.由此,循环统计量公式可化为

由于P是正交矩阵,所以P-1=PT,检验统计量也可表示为


表1 协方差矩阵的特征值Table1 Covariance matrix eigenvalues

最后,从统计量的计算公式角度来看,经典的循环统计量算法,如式(5),实质是二次型计算,循环自相关函数向量的协方差矩阵估计xx(*)的逆矩阵可作为二次型的系数矩阵.从二次型的结构可见,由于二次型的系数矩阵为协方差矩阵的逆矩阵,相关性强的两项的乘积系数反而更小.因此,统计量的计算实质是突出了不相关.为进一步突出不相关,可将协方差矩阵对角化,使协方差矩阵的能量都集中在主对角线上,相关性强的两项乘积系数将更小.
2.2 基于特征值矩阵的循环平稳检测
综上所述,本研究提出基于循环自相关向量的协方差矩阵的特征值矩阵的统计量计算方法,用协方差矩阵的特征值矩阵代替原有的协方差矩阵.该特征值矩阵不但使信号的信息更集中,且不含正交矩阵,因此可保留循环自相关函数向量之间的所有信息,使得信号的相关信息在循环统计量计算过程中得到充分利用.本研究提出的循环统计量公式为

为采用恒虚警概率检测方法,需判断统计量在H0下服从什么分布.在H0的假设下,估计误差向量只包含高斯噪声的循环自相关向量ε1.当噪声是均值为零的高斯白噪声时,采样值互不相关,所以近似协方差矩阵为对角阵.此时,协方差矩阵可为


因此,在H0下,基于特征值矩阵的统计量与原循环统计量相同,且服从自由度为2N的卡方分布,即

综上所述,计算基于特征值矩阵的循环统计量的方法为:首先,根据式(12)计算T'xx(*);然后,根据式(15)确定判决门限λ,使虚警概率满足Pf;最后,根据统计量T'xx(*)与门限λ的关系,判决信号是否存在.
2.3 定性比较两种循环统计量
为比较两种循环统计量计算方法,本研究比较了两种统计量统计意义上的大小.
设二次型为Y=rTAr,其中 r为高斯随机向量,其对角化为其中,λk为二次型矩阵的某个特征值;mk为该特征值的重复度;此时,二次型的数学期望[9]为

根据式(16)分别计算两种循环统计量计算方法(式(5)和式(12))的数学期望.为便于推导,设协方差矩阵∑xx(*)的特征值各不相同,则mk=0.此时,两种统计量计算公式的数学期望为(将期望公式中的系数1/2省略)

其中,λ=[λ1λ2… λ2N]为协方差矩阵所有特征值构成的行向量;r=[r1r2…r2N]为循环自相关函数构成的行向量;L=rP=[l1l2…l2N]为循环自相关函数向量经过正交变换后的向量;L2=Ldiag(L)为向量L线性变换后的向量;r2=rdiag(r)为向量r线性变换后的向量;符号表示向量长度.
由式(17)和式(18)可知,循环统计量的数学期望可表示成向量内积形式.向量内积(a,b)的几何意义为:向量a的长度乘以向量b在a上的投影的长度.式(17)和式(18)的空间关系如图1.若比较两种统计量的数学期望,则要比较L2与r2在λ上的投影长度.而L2与r2分别由L与r通过线性变换得到,即向量角度的旋转和长度的缩放.在信噪比较低时信号幅度较小,计算得到的循环自相关函数向量较小,因L与r的长度不变,得L2<.因此,L2在λ方向上的投影小于r2在λ方向上的投影.综上所述,E(T)<E(T').因此,基于特征值矩阵的循环统计量在统计意义上优于经典的循环统计量.

图1 向量之间的关系Fig.1 Vector relationship
2.4 计算复杂度分析
循环平稳特征检测的一个缺点是计算复杂度高,基于特征值矩阵的循环平稳特征检测方法可降低计算复杂度.下面我们将比较两种计算循环统计量方法的复杂度.比较式(5)和式(12),因系数M对于计算复杂度的比较无影响,所以只考虑向量矩阵之间的运算.式(12)和式(5)各自所需加法及乘法的次数如表2.
此外,求矩阵的特征值最有效和可靠的算法是QR(quadrature right-triangle)算法,其计算量[10]为4/3×n3.因为循环统计量中的求逆运算为伪逆,而求矩阵伪逆采用初等变换法的计算量[11]为10/3×n3.其中,n为矩阵的维数,所以求矩阵特征值要比求矩阵伪逆计算简单.用Matlab软件计算得到协方差矩阵特征值和伪逆的运行时间分别为1.132 2×10-4s和0.033 8 s.因此,基于特征矩阵的循环平稳检测算法比经典的循环平稳特征检测算法计算更简单,从而降低了循环统计量的计算复杂度.

表2 计算复杂度比较Table2 The comparison of computational complexity
2.5 多循环求和循环平稳检测
由于不同循环频率的循环自相关函数是近似不相关的,可推得基于特征值矩阵的多循环频率求和检测器的检验统计量为[6]

其中,Tm为采用多循环频率时的检验统计量.统计量的分布在H0假设下保持不变,服从卡方分布,自由度为2NNα,Nα是循环频率的个数.
3 仿真性能分析
设待测的主用户信号是基带OFDM信号,表示为[6]
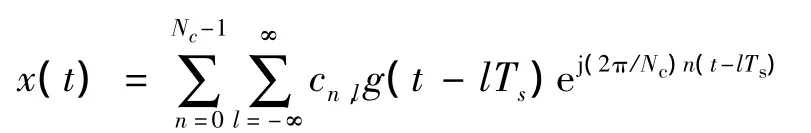
其中,Nc是载波个数;Ts=Td+Tcp是符号长度,Td为有用符号的长度,Tcp是循环前缀的长度;g(t)表示长度为Ts的矩形窗;cnl是数据符号.仿真中使用的循环频率是1/Ts和2/Ts,检测器的时间延迟为±Td.循环谱估计中使用的是长度为61,β是参数为10的Kaiser窗,信号总长度为125个OFDM符号.信噪比(signal to noise ratio,SNR)定义为 γ=10lg(σ2x/σ2n),其中σ2x和σ2n分别是发射信号和噪声的方差.仿真采用蒙特卡罗试验,图2~图8中的曲线都是由500次试验平均而得.
首先,在高斯白噪声下,比较经典的循环平稳检测方法和基于特征矩阵的循环检测方法的性能,描述检测概率pd和γ的关系.
图2描述了在虚警概率pf=0.01时的两种检测方法的检测概率的比较结果.其中,MY表示基于特征矩阵的循环平稳检测的检测结果;Cycle表示经典循环平稳检测的检测结果.由图2可知,基于特征值矩阵的检测概率比经典循环平稳检测方法在低信噪比时有所提高.为证明此方法对于其他虚警概率依然具有良好的性能,表3给出了在不同虚警概率时仿真得到的检测概率比较结果.其中,检测概率1是经典循环平稳检测方法下的检测概率,检测概率2是基于特征矩阵循环平稳检测的检测概率.

图2 单循环频率的检测概率与信噪比的关系Fig.2 Relationship between probability of detection and SNR
为验证基于特征值矩阵循环平稳检测算法在多循环频率时依然适用.图3描述了两种检测方法在两个循环频率时的检测结果.其中,Two-Cycle是经典算法使用两个循环频率的检测结果;MY指基于特征值矩阵的循环平稳检测算法使用两个循环频率时的检测结果.由图3可知,在多循环频率下,基于特征值矩阵的循环平稳检测算法优于经典的循环平稳检测.

表3 两种检测方法在不同虚警概率时的检测概率的比较Table3 The comparison of probability of detection with different probability of false alarm

图3 两种方法使用多循环频率时检测概率与SNR的关系Fig.3 Comparison of probability of detection between two methods
由于无线环境是实时变化的,因此噪声具有不确定性.为验证基于特征矩阵的循环平稳检测对噪声是不敏感的,图4和图5比较了当噪声存在0.170 3 dB的不确定时的两种方法检测结果.由图4和图5可知,当噪声存在不确定时,检测性能不受影响.因此,循环平稳检测对噪声是不敏感的.图4表明,当噪声存在不确定时,基于特征矩阵的检测性能优于经典循环平稳检测方法.比较图2和图4可知,噪声存在不确定时,检测概率并没有下降.图5描述两种方法在噪声存在不确定时采用多循环频率的检测结果.

图4 在噪声存在不确定时单循环频率检测概率的比较Fig.4 Relationship between probability of detection and SNR with noise uncertainty

图5 噪声存在不确定时两种检测方法使用多循环频率的检测结果的比较Fig.5 Comparison of detection probability between the two methods with noise uncertainty
结 语
本文通过分析经典循环平稳检测算法发现,在计算循环统计量的过程中,循环自相关函数向量被正交化,各元素之间的相关性被消除,因此原始信号的信息在统计量计算过程中有一定损失.因此,本文改进了循环统计量的计算方法,提出基于特征值矩阵的循环平稳特征检测.仿真结果表明,在高斯白噪声背景下,无论噪声是否存在不确定,基于特征值矩阵的循环平稳检测方法的检测性能优于经典的循环平稳检测方法.此外,基于特征矩阵的循环平稳检测算法降低了计算复杂度.
/References:
[1]CHEN Xiao-fei,Nagaraj S V.Entropy based spectrum sensing in cognitive radio[J].Wireless Telecommunications Symposium,2009,89(2):174-180.
[2]Cabric D,Mishra S M,Brodersen R W.Implementation issues in spectrum sensing for cognitive radios[C]//Proceedings Asilomar Conference on Signals,Systems,and Computers.Grove:IEEE Computer Society,2004,1:772-776.
[3]Lunden J,Koivunen V,Huttunen A,et al.Spectrum sensing in cognitive radios based on multiple cyclic frequencies[C]//Cognitive Radio Oriented Wireless Networks and Communications.Orlando:IEEE Computer Society,2007:37-43.
[4]Mishra S M,Sahai A,Brodersen R W.Cooperative sensing among cognitive radios[C]//IEEE International Conference on communications.Istanbul:IEEE Press,2006,4:1658-1663.
[5]Renzo M D,Imbriglio L,Fabio G,et al.Cooperative spectrum sensing for cognitive radios:performance analysis for realistic system setups and channel conditions[C]//Mobile Lightweight Wireless Systems.Berlin:Springer,2009,13:125-134.
[6]Lunden J,Koivunen V,Huttunen A,et al.Collaborative cyclostationary spectrum sensing for cognitive radio systems[J].IEEE Transactions on Signal Processing,2009,57(11):4182-4195.
[7]GOH L P,LEI Zhong-ding,FRANCOIS C.DVB detector for cognitive radio[C]//IEEE International Conference on Communications.Glasgow:IEEE Press,2007:6460-6465.
[8]Dandawate A V,Giannakis G B.Statistical tests for presence of cyclostationarity[J].IEEE Transactions on Signal Processing,1994,42(9):2355-2369.
[9]Raphaeli D.Distribution of Noncentral indefinite quadratic forms in complex normal variables[J].IEEE Transactions on Information Theory,1996,42(3):1002-1007.
[10]HU Mao-lin.Matrix Calculation and Application [M].Beijing:Science Press,2008:171-187.(in Chinese)胡茂林.矩阵计算与应用 [M].北京:科学出版社,2008:171-187.
[11]YAO Li-hui.Research on Calculation and Application in Matrix Equation of the Generalized Inverse Matrices[D].Zhengzhou:PLA Information EngineeringUniversity,2008.(in Chinese)尧礼辉.广义逆矩阵计算及在矩阵方程中应用的研究[D].郑州:解放军信息工程大学,2008.

