基于矩形代数和公共模式方法的相似图像检索

刘大有，董 婥，王生生

吉林大学计算机科学与技术学院，长春130012

基于空间关系的CBIR算法［1］(content-based image retrieval，CBIR)，主要依据图像中对象之间的空间关系进行相似性检索.近十多年来，一些基于空间关系的CBIR算法陆续被提出.Gudivada等［2］提出的SIMR算法及 El-Kwae等［3］扩展SIMR得到的SIMDTC算法，将对象抽象成几何中心点，利用两点之间的角度描述对象间的空间关系，忽略了对象自身大小.WANG［4-5］等提出基于2D BE-string排序的最大公共子序列(longest common subsequence，LCS)算法.基于LCS的算法考虑物体在两个维度的排列顺序，无法精确描述区域间的空间拓扑关系.Hsieh等［6］提出公共模式方法(common pattern method，CPM)，随后又提出将图像中所有对象及对象间方位关系表示为空间关系图(spatial relationship graph，SRG)，用两个SRG的公共顶点和公共边的总数度量相似性［7］.这两个方法同样将对象抽象成几何中心点，仅利用两点之间的方位排序进行检索，不仅导致检索出了不相关的图像，且耗时，无法满足互联网上快速响应的需求.Chiang等［8］提出将对象抽象成最小边界矩形(minimum bounding rectangle，MBR)，将MBR一维上的空间关系映射为ING(interval neighbor group)的一个顶点，对象间距即为两个维度上ING顶点的最短路径之和，对象间距离越远说明相似性越低.Wang等［9］在MBR表示物体的基础上，考虑对象间z轴方向的距离，得到复合的方位关系并计算方位距离.以上两种方法需计算所有对象间距，当图像中对象规模为n时，需进行n×(n-1)/2次计算.这些方法中.CPM是一个平均比较时间最短，且具兼容性的方法，尤其是在对象较多或符号重复率较高的情况下，仍满足多项式时间复杂性［6］，是目前较好的相似性算法之一.实验说明，CPM的检索速度是基于LCS的团集LCS_clique的30倍，是SIMR、SIMDTC和2D BE-string的8～10倍［6］.随着对象数目或符号重复率的增加，LCS_clique、SIMR和SIMDTC的检索时间将会激增，而CPM仍保持稳定的速度，满足多项式时间的复杂性［6］，CPM的检索效果比9DLT 的检索效果更好［10］.

由于CPM采用基于点的空间模型，无法检索出精确结果.为此，本研究基于CPM，将图像中的对象抽象为MBR，采用矩形代数描述对象间的空间关系，得到基于矩形代数的相似性图像检索算法(similarity retrieval by rectangle algebra，SRRA).SRRA关于对象间的相似性度量比CPM更严格，在计算最大相似对象集合的过程中，可有效减少不相关对象的计算，不仅得到更准确的检索结果，且显著缩短了检索时间.

1 研究背景

1.1 矩形代数(rectangle algebra)

1983年，Allen［11］提出基于连续区间的时态推理系统，即区间代数.区间代数中定义了13种基本关系，每个基本区间关系描述两个时间段的确定关系.Balbiani等［12］将 Allen时态区间代数扩展到二维空间，得到矩形代数，所描述的空间对象是四边平行于二维直角坐标的矩形，如图1.

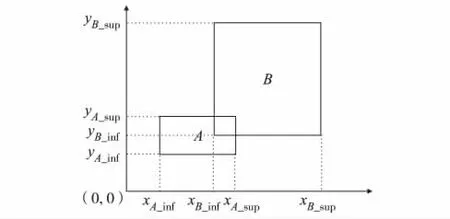
图1 矩形代数描述的空间对象Fig.1 The objects described by rectangle algebra

矩形代数关系的定义为［13］

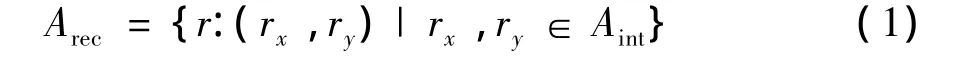
其中，Aint={p，pi，m，mi，e，d，di，s，si，f，fi，o，oi}，如表1.Arec构成一个互不相交且联合完备(jointly exhaustive and pair wise disjoint，JEPD)的关系集合，它包含矩形所有关系［14］.尽管 Hoàng等［15］提出新的空间关系制图法，矩形代数仍因其易于理解、良好的计算性质和推理方法被广泛采用.

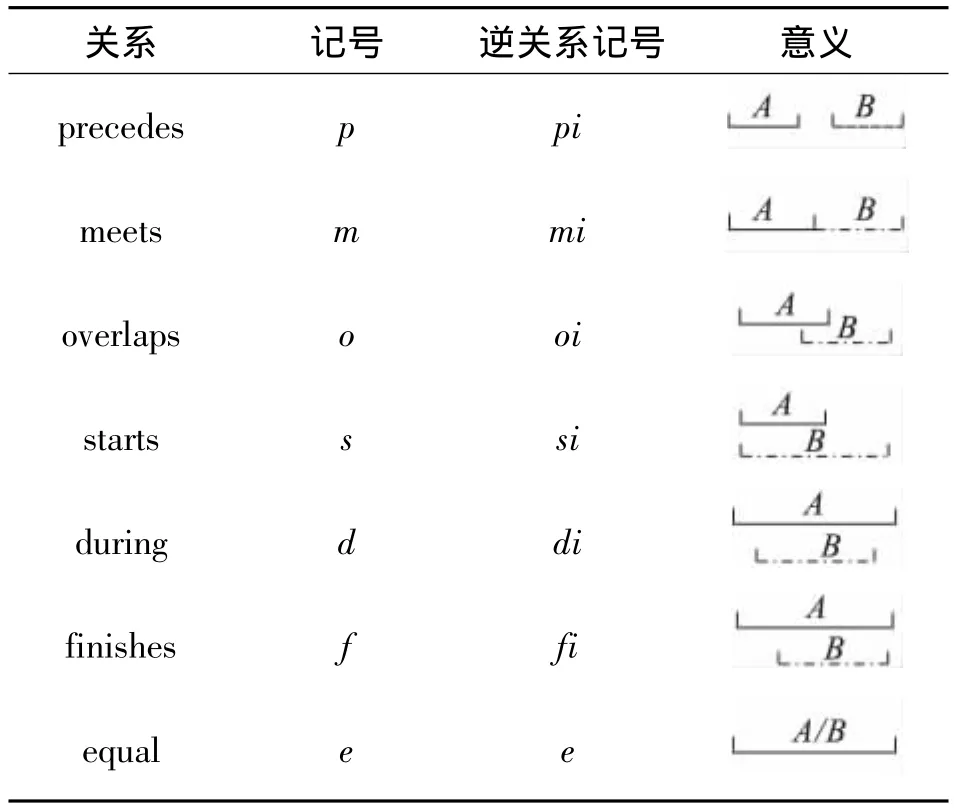
表1 矩形代数的13种基本关系Table1 The basic relationships of rectangle algebra

1.2 LCS_clique

1989年，Lee等［16］提出 LCS_clique算法利用两个2D string构建一个type-i公共子图，通过寻找其最大团，求得两幅原始图像的最大公共子图.

type-i公共子图的定义为［6］

令S为图像f1的对象子集，T为图像f2的对象子集.若存在一个从S到T的双射函数满足:①S中对象Oi的符号等于g(Oi)的符号;② 对于S中任意两个对象Oi和Oj，f1中的Oi和Oj是type-i相似的，同时f2中的g(Oi)和g(Oj)也是type-i相似的(其中i=0，1，2)，我们说S和T是f1和f2的type-i公共子图.

1.3 CPM

2008年，Shu-Ming Hsieh等提出用CPM解决图像检索问题.CPM将图像中对象抽象成几何中心点，采用type-i方法度量对象间的相似性.利用LCS_clique思想，CPM将无向的type-i公共子图转化为一组有向无环的CP_DAG图，将在type-i公共子图内寻找最大团的问题转化为在这一组CP_DAG内寻找最长路径的问题.最长路径上的顶点构成最大的相似对象集合，集合内所有对象的相似值加和是两图的相似值.

与 LCS_clique、SIMR、SIMDTC及2D BE-string 相比，CPM是一个平均比较时间最短的算法.一般来说，CPM的检索速度是LCS_clique的30倍，是SIMR、SIMDTC和2D BE-string的8 ～10倍［6］.同时，随着对象数目或符号重复率的增加，LCS_clique、SIMR和SIMDTC的检索时间将会激增，而CPM仍保持稳定的速度，满足多项式时间的复杂性［6］.

但是，CPM无法精确描绘对象间的空间关系.采用type-i方法判断两点的方位关系，忽略了对象自身的大小，基于点的空间模型无法描述区域间的拓扑关系.例如，两物体呈现meet和overlap等不同拓扑关系时，CPM易将其表示成相同的方位关系，从而认为物体具有较高的相似性.这既不能很好地区分图像，还会因为判断空间相似性不严格，增加冗余计算，使检索过程费时费力.

2 SRRA算法

本研究基于CPM，将图像中对象抽象为MBR，用矩形代数描述对象间的空间关系，从而改进得到SRRA算法.算法步骤为

①建立符号化图像数据库.把图像中对象抽象成MBR并标注对象的符号(symbol)，即每个对象表示为(［xinf，xsup］，［yinf，ysup］，symbol)这样的三元组.每张图像按照所有对象的xinf坐标从小到大将对象排序.例如，查询图像f1可表示为α=a1a2...an1，数据库图像 f2可表示为 β =b1b2...bn2.这样，我们不再需要存储图像本身，只要存储一串三元组即可.

②建立顶点数组M.当ai.symbol=bj.symbol时，生成顶点(i，j)，并将其放入顶点数组M.为便于计算，用vk表示M中第k个顶点.注意，这里的顶点并不代表一个对象，而是具有相同符号的两个对象构成，即vk=(i，j).

③构造SRRA中的矩形代数相似图(rectangle algebra similaritygraph，RASG)，其函数记作construct_RASG()，具体构建步骤如图2.

RASG的顶点来自M的元素，对于RASG()的任意两点vm和vn，设vm=(i，j)，vn=(o，p)，若满足i＞o且j＞p，同时，ai和ao存在某种矩形代数关系r，而 bj和bp存在相同的矩形代数关系 r，RASG()存在有向边 ＜vm，vn＞.

生成RASG(i，j)的步骤为

i)RASG(i，j)的第一个顶点为(i，j);

ii)对所有 RASG(k，h)，k ＜ i，h ＜ j，求得其中和顶点(i，j)具有相同的空间关系的顶点以及相应的有向边.考察顶点(i，j)和(k，h)是否具有相同的空间关系，需分别在x轴和y轴上判断对象的投影范围属于哪种矩形代数基本关系(表1)，相应算法为 Algorithm RA((i，j)，(k，h)). 当 求 得RASG(k，h)中和顶点(i，j)具有相同的空间关系的顶点以及相应的有向边之后，需要将其全部加入RASG(i，j).这是RASG(i，j)的扩展过程，表示按顺序扫描到(i，j)为止，包含(i，j)的最大相似对象集合;

iii)扩展RASG(i，j)的具体情况可分为:一，若RASG(k，h)中仅(k，h)和(i，j)具有相同矩形代数关系，则直接在RASG(i，j)中增加顶点(k，h)，增加一条从(i，j)到(k，h)的有向边，并给这条有向边赋值一个新的pID;二，通常称RASG(k，h)中和(i，j)具有相同的矩形代数关系的顶点组成的集合为SV，相应的有向边集合为SE，且＞1.对于任意路径p'∈SE，将该路径上的所有顶点和边依次加入RASG(i，j)，同时增加从(i，j)到(k，h)的有向边，设路径号为p'，则该有向边成为路径 p'的一部分.生成算法见Algorithm Construct_RASG((i，j)).

图2 Algorithm SRRA()构建步骤Fig.2 Construct Algorithm SRRA()

④针对M中的每个元素(i，j)生成RASG(i，j)，并依此得到当前图中的最长路径pi.最后，在集合{pi}中寻找最长路径pmax.pmax上的所有顶点即最大相似对象集合.

下面将给出最长路径上的顶点即构成最大相似对象集合的正确性说明.

传统方法利用最大团解决图像检索问题需构建一个无向图，其每个顶点和RASG顶点定义一致;无向图中的边表示连接的两个顶点所代表的对象之间具有相同矩形代数关系.设无向图的顶点数为N，则在构建无向图的过程中，需考察每个顶点和其余N-1个顶点的关系.在求解最大团的过程中，还需不断考察任意顶点和其他顶点是否相邻.

由SRRA算法可知，构建RASG(i，j)需不断扩展，将RASG(k，h)中和(i，j)具有相同的矩形代数关系的顶点及相应的有向边合并入RASG(i，j)，其中k＜i，h＜j，且只需考虑符合这种关系的顶点.考虑两种扩展RASG(i，j)的情况:

第一种情况，当RASG(k，h)中和(i，j)具有相同矩形代数关系的顶点集合内只有一个顶点(k，h)，不存在相应的有向边时，将(k，h)加入RASG(i，j)，并增加一条从(i，j)到(k，h)的有向边，同时分配该边新的ID路径编号.此时该路径长度为1，路径上两个顶点具有相同矩形代数关系.

第二种情况，设RASG(k，h)中和(i，j)具有相同矩形代数关系的顶点集合为SV，相应的有向边集合为SE，＞1.考虑任意路径pID∈SE，设其长度为n.

根据第一种情况可知，每条边上的两点所代表的对象具有相同的矩形代数关系，且在加入的过程中，当前加入的顶点和路径的起始点也具有相同的空间关系，那么路径上的n+1个顶点所代表的对象中，任意两个对象间均具有相同的矩形代数关系，且由于pID∈SE，路径上的n+1个顶点也都属于集合SV，所以这n+1个顶点也都和(i，j)具有相同的矩形代数关系.当把pID路径上的边和顶点依次加入RASG(i，j)时，需要增加一条从(i，j)到(k，h)有向边并为其赋值pID.此时，路径的长度变成n+1，并且这n+2个顶点中任意两个顶点的矩形代数关系也保持一致.因此，这条路径表示的意义同无向图中最大团的意义是一样的.至此，我们把求无向图的最大团问题转化为求有向图中最长路径的问题.

同时，从算法中可见，构建RASG(i，j)时只考虑RASG(k，h)，其中，k＜i，h＜j;同时，若RASG(k，h)中第一个顶点(k，h)和(i，j)不满足相同的空间关系，则RASG(k，h)其余顶点均不必再考察，这个候选图RASG(k，h)直接被删减掉.这样，求解最长路径问题比求解最大团问题显著减少了时间.

3 结果分析

3.1 实验数据

本实验数据分为人工构造数据集和Simplicity system数据库.人工构造数据集用来比较SRRA和CPM的检索时间，Simplicity system数据库用来比较SRRA和CPM的检索效果.为与CPM使用的对象信息一致，本研究在构造每个对象的MBR时随机生成对象符号、(xinf，yinf)坐标和最小外界矩形的长l、宽w，则xsup=xinf+l，ysup=yinf+w，对象的几何中心点表示为(xcen，ycen)，其中xcen=(xinf，xsup)/2，ycen= (yinf，ysup)/2;Simplicity system 数 据 库(http://wang.ist.psu.edu/docs/related/)需要人工对图像进行符号标注处理，这个过程对应算法SRRA建立符号化图像数据库的过程.

3.2 实验结果

本实验测试环境为:处理器Intel(R)Core(TM)2 Duo CPU E7500 2.93 GHz，内存 2G，硬盘160 G，操作系统为Windows XP，编程环境为Visual Studio 2008.

首先复原CPM，然后基于CPM改进得到SRRA.图3是SRRA与CPM随着图像中对象数目不同，每图所需检索时间对比结果.

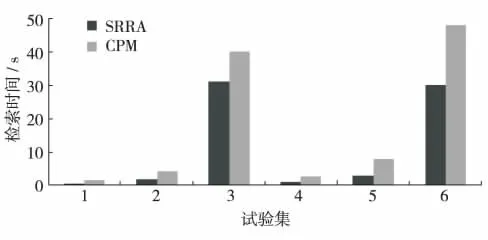
图3 SRRA与CPM平均一次的检索时间对比Fig.3 The average cost of SRRA and CPM

测试集1～3中每组包括1 000张图像，每张图包含的对象数分别是5、10和15;测试集4～6中每组2 000张图像，每张图包含的对象数分别是5、10和15.由图3可见，SRRA算法在各组测试集上的检索时间均远小于基于CPM的算法.这是因为CPM算法用type-i方法判断对象的相似性，会将很多原本不同的拓扑关系表示为相同的方位关系，所以在构建CP_DAG的过程中，不相关的顶点和空间关系都被加入CP_DAG，构建时间显著增加.SRRA算法采用的矩形代数比type-i需要更复杂的判断，使时间略增，但检索过程中空间关系判断的耗时极少，大部分时间都用来构建RASG，而矩形代数能严格衡量空间关系相似，所以构建RASG过程中可扩展的顶点和边都很少，构建时间显著缩短.在检索大对象数目时，SRRA算法优势明显，如图3中第3组和第6组对比结果.图4对比了SRRA算法和CPM算法模拟检索耗时.测试集7～8每组包括1×105张图片，每张图片包含的对象数目分别是5张和10张.用这组模拟数据考察图像数目多，每张图像内包含对象数目小的特点.由图4可知，在海量数据中检索图像时，SRRA较CPM可缩短一半的检索耗时.

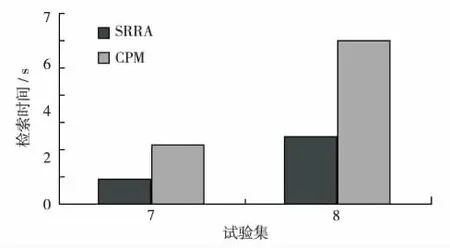
图4 对比SRRA与CPM在1×105张图片中检索1张的耗时Fig.4 The total cost of SRRA and CPM running on massive image database

关于CPM和SRRA的说明:

①在对象投影到x轴和y轴上的线段均是彼此分离的情况下，基于CPM的算法和SRRA算法的相似性度量结果一致，基于CPM的算法效率更高，这种情况在现实中很少发生;

②当两幅图中仅有一组符号相同的对象时，只能得到其位置信息，无法得到对象间的空间关系，此时CPM和SRRA都不适用，这种情况在实际检索中也较罕见.

图5是SRRA和CPM在Simplicity system数据库以5(a)为查询图像推荐结果，图5(b)是SRRA推荐的7幅图像，图5(b)和(c)是CPM推荐的13幅图像.相似性图像检索只需两图像中对象集合有交集即可，所以图5(b)和(c)中可出现多个对象.设图5(a)棕色马为A，白马为B.CPM仅比较对象的几何中心点的方位关系，图5所有图像中A的中心点均位于B的中心点的NS方向，故CPM推荐(b)、(c)两组图像;(a)中A和B投影在x轴的关系是precede，在y轴的关系是start，而(c)中A和B在x轴的关系是overlap，SRRA认为图5(c)中A和B的拓扑关系与图5(a)中A和B的拓扑关系不一致，故SRRA不推荐图5(c)的图像.在本实验中，若把最大相似对象数目为2的图像推荐为检索结果，则CPM推荐的结果大约比SRRA推荐的结果多50%，而这50%的结果多为不能严格满足拓扑关系的图像，这在后续的相关反馈步骤里也会给用户带来复杂的选择.

图5SRRA和CPM的推荐结果Fig.5 The recommended result of CPM and SRRA

结 语

本研究在CPM的基础上，采用矩形代数描述对象间的拓扑关系，提出基于矩形代数的相似性图像检索算法SRRA.在8组人工构造测试数据集和Simplicity system数据库上对两种算法进行了实验对比，结果表明，SRRA不仅在时间上优于CPM，且检索结果更符合用户需求.下一步，我们将在SRRA算法的基础上引入相关反馈算法［17-18］.由于传统的相关反馈算法大都针对数值化特征向量进行修正，在基于空间关系相似性的CBIR中无法使用［19］，因此，在未来研究中，我们将致力于把所有图像符号化后求得的字符串看做一个有序数据库，针对有序数据库进行序列模式挖掘，以此找到用户选择的正例集合中有效的空间信息;根据空间关系具有复合的性质，我们打算采用矩形代数基本关系复合、路径一致原理［20］相结合的方法，完成空间关系的复合计算，达到查询图像重定义的目的.

/References:

［1］Datta R，Joshi D，LI Jia，et al.Image retrieval:ideas，influences，and trends of the new age ［J］.ACM Computing Surveys，2008，40(2):1-60.

［2］Gudivada V N，Raghavan V V.Design and evaluation of algorithms for image retrieval by spatial similarity ［J］.ACM Transactions on Information Systems，1995，13(2):115-144.

［3］El-Kwae E A，Kabuka M R.A robust framework for content-based retrieval by spatial similarity in image databases［J］.ACM Transactions on Information Systems，1999，17(2):174-198.

［4］WANG Ying-hong.Image indexing and similarity retrieval based on spatial relationship model［J］.Information Sciences，2003，154(1/2):39-58.

［5］YIN Peng-yeng，LIU Chin-wen.A new relevance feedback technique for iconic image retrieval based on spatial relationships ［J］.The Journal of Systems and Software，2009，82(4):685-696.

［6］Hsieh Shu-Ming，Hsu Chiun-Chieh.Retrieval of images by spatial and object similarities［J］.Information Processing and Management，2008，44(3):1214-1233.

［7］Hsieh Shu-Ming，Hsu Chiun-Chieh.Graph-based representation for similarity retrieval of symbolic images ［J］.Data and Knowledge Engineering，2008，65(3):401-418.

［8］Chiang J Y，Cheng Shuenn-ren，Huang Shuenn-Reng，et al.Multiple-instance image database retrieval by spatial similarity based on interval neighbor group［C］//Proceedings of the ACM International Conference on Image and Video Retrieval CIVR'10.Xi'an(China):ACM Press，2010:135-142.

［9］Wang Hui-hui，Mohamad Dzulkifli，Lsmail N A.Semantic gap in CBIR:automatic objects spatial relationships semantic extraction and representation［J］.International Journal of Image Processing，2010，4(3):192-204.

［10］Rezaei-Kalantari Kimia，Eftekhari-Moghadam A M.Symbolic image indexing and retrieval by spatial similarity:a new approach based on multi-dimensional B+tree［C］//The 4th International Conference on New Trends in Information Science and Service Science(NISS).Gyeongju(Korea):［s.n.］，2010:145-152.

［11］Allen J F.Maintaining knowledge about temporal intervals［J］.Communications of the ACM，1983，26(11):832-843.

［12］Balbiani P，Condotta J F，L Del Cerro L F.A new tractable subclass of the rectangle algebra［C］//Proceedings of the 16th International Joint Conference on Artificial Intelligence.San Francisco(USA):Morgan Kaufmann Publishers，1999:442-447.

［13］CHEN Juan.Research on Spatial Directional Relation Models and Integrative Reasoning of Multi-aspect Spatial Relations［D］.Changchun:Jilin University，2011.(in Chinese)陈 娟.空间方位关系模型及多方面空间关系结合推理的研究 ［D］.长春:吉林大学，2011.

［14］DONG Yi-qun.Research on Some Problems of Qualitative Spatial Direction Relations Modeling［D］.Changchun:Jilin University，2011.(in Chinese)董轶群.定性空间方向关系建模中若干问题研究［D］.长春:吉林大学，2011.

［15］Hoàng Nguyen Vu，Gouet-Brunet Valérie，Rukoz Marta.A cartography of spatial relationships in a symbolic image database［J］.Proceedings of the 14th International Conference on Computer Analysis of Images and Patterns:Part I.Berlin:Springer-Verlag，2011，6854:377-385.

［16］Lee Suh-yin，Shan Man-kwan，YANG Wei-pang.Similarity retrieval of iconic image database［J］.Pattern Recognition，1989，22(6):675-682.

［17］LIU Lin，LI Ren-fa，LI Zhong-sheng，et al.Research on relevance feedback in contrent-based image retrieval［J］.Application Research of Computers，2009，26(7):2427-2431.(in Chinese)刘 琳，李仁发，李仲生，等.基于内容图像检索中的相关反馈技术研究 ［J］.计算机应用研究，2009，26(7):2427-2431.

［18］XU Xiang-li，ZHANG Li-biao，LIU Xiang-dong，et al.Image retrieval relevance feedback algorithm based on particle swarm optimization ［J］.ACTA Electronica Sinica，2010，38(8):1935-1940.(in Chinese)许相莉，张利彪，刘向东，等.基于粒子群的图像检索相关反馈算法 ［J］.电子学报，2010，38(8):1935-1940.

［19］YIN Peng-yeng，LIU Chin-wen.A new relevance feedback technique for iconic image retrieval based on spatial relationships ［J］.The Journal of Systems and Software，2009，82(4):685-696.

［20］XING Shi-mei.Research on Consistency Techniques in Constraint Satisfaction Problems［D］.Changchun:Jilin University，2011.(in Chinese)邢士美.约束满足问题中相容技术的研究 ［D］.长春:吉林大学，2011.