基于可整平基准尺的工业测量定向方法

景 冬，卢秀山，郑文华，于胜文，王婷婷

山东科技大学测绘科学与工程学院，山东青岛266590

工业测量系统(industrial measuring system，IMS)是通过光学角度测量仪器对部件、产品及构筑物进行非接触和实时三维坐标测量，并在现场进行测量数据的处理、分析和管理的应用系统［1-2］，其构成如图1.作为测量技术的一个新的应用领域，IMS在制造业、大型工程等方面得到广泛应用［3］.

现有的工业测量系统主要采用2台以上设备以互瞄观测方式行相对定向［4］，因此系统多采用安装有互瞄用内觇标的专用电子经纬仪作为角度测量仪器，此类专用仪器应用范围较小，系统价格昂贵.为降低设备采购成本，如何将同等精度非专用测量设备应用于工业测量领域，并提高工业测量系统在国内的应用程度就显得尤为重要［5］.

图1 工业测量系统的构成Fig.1 Configurations of industrial measuring system

本研究结合自行设计的可整平基准尺，提出新的系统定向模型，采用同级别测角设备代替0.5″级高精度专用电子经纬仪，展开新型非互瞄工业测量系统的研究［6］.

1 基于可整平基准尺的空间后方交会

假设经整平后基准尺的两个观测点为S1和S2，其水平投影距离和高差分别为D和H.基于该定向模型的基准尺，观测时需将S1、S2、D及H借助辅助整平装置 (如符合水准管、电子水准仪)调整到固定值，即两点在空间的相对位置一定.本文将满足该条件的基准尺称为可整平基准尺，如图2.

图2 可整平基准尺Fig.2 Adjustable scale bar

为理解基于可整平基准尺的空间后方交会原理，首先以基准尺为参照，建立物方空间直角坐标系.设S1点作为基准尺坐标系坐标原点O，基准尺边S1S2在水平面上的投影为x轴，通过O点铅垂向上为z轴，y轴使坐标系符合右手法则.如图3.

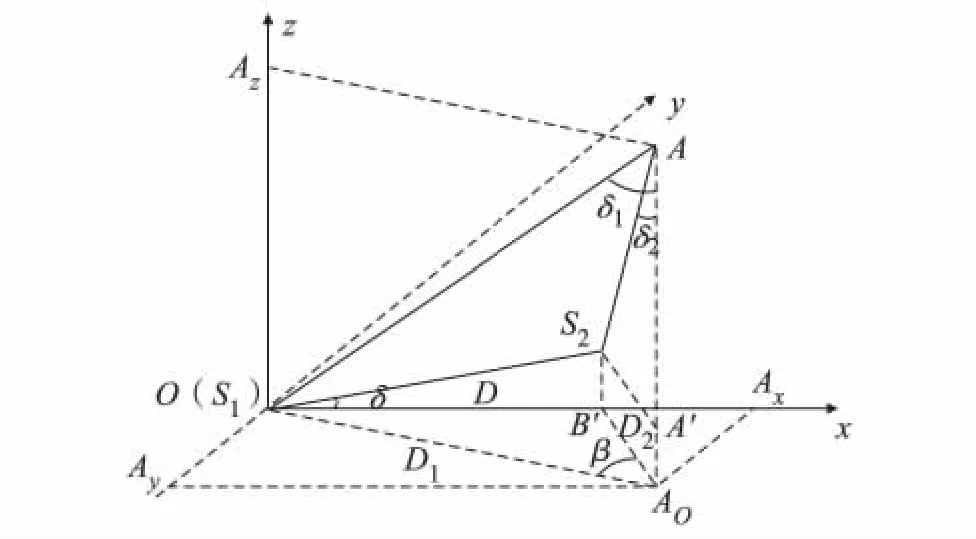
图3 基于可整平基准尺的空间后方交会Fig.3 Spatial resection base on the adjustable scale bar

假定为左盘观测值，分别观测基准尺上两点O(S1)和S2，得水平、垂直方向值分别为β0、α0和β1、α1. 因此，水平角 β 为视线与铅垂线所成的角度为δ0和δ1.设两点在基准尺坐标系中高程分别为H1和H2;S1点至测站仪器中心A的水平距离为D1，S2至A的水平距离为D，A点的高程为H，则

解方程

其中±可由两竖直方向天顶距大小判断，从而达到采用测量边前方交会，获得测站在基准尺坐标系下的平面坐标.

测站坐标(xA，yA，zA)分别为

对基准尺两目标点S1和S2竖直角观测值进行计算，单个盘面 (盘左或盘右)均可解算出测站所采用的电子经纬仪 (electronic theodolite)在基准尺坐标系下的高程h'T和h″T，且单个仪器中心定位与其它仪器无关，因而取

为提高观测精度，可对基准尺进行盘左与盘右双盘面观测，这就能进一步减小观测误差及测角仪器的读数误差.

对于该定向模型，由于在定向观测过程中，需要目标观测点S1和S2的两点水平投影距离D和高差H已知，因而要求两点的空间相对位置为定值.

2 非互瞄系统定向

2.1 相对定向

在非互瞄三维工业测量系统中，由于所采用的电子经纬仪、全站仪等测角仪器均无或不使用内觇标，因而不能直接互瞄进行相对定向，测站间相对定向参数需间接计算得出［7-8］.

非互瞄定向 (non-mutuolly collimate orientation principle，NMCO)三维工业测量系统中目标观测及数据处理采用前方交会的方法，为方便数据处理，宜采用测站坐标系作为观测坐标系.测站坐标系以测站中心A点作为原点O，基线AB为x轴，通过基线铅垂向上为z轴，y轴使坐标系符合右手法则.

基准尺坐标系以基准尺观测点S1点作为基准尺坐标系坐标原点O，基准尺S1S2边在水平面上的投影为x轴，通过基准尺观测点S1竖直向上为z轴，y轴使坐标系符合右手法则.基准尺坐标系与测站坐标系均为空间直角坐标系，其坐标系转换仅限于坐标原点的变换及水平面坐标绕z轴的旋转角值κ.

基准尺坐标系原点O与测站坐标原点A间的坐标转换参数为其中，Δx、Δy和Δz分别为坐标原点O测站在基准尺坐标系下，平移到标原点A在x轴、y轴和z轴增量.

水平面x轴与y轴转换所需的z轴旋转角θ为

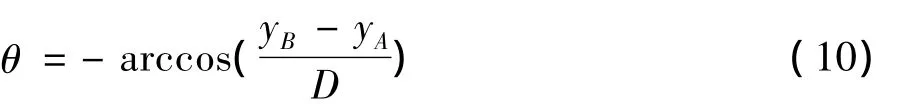
测站观测基准尺目标点各方向线与基准尺坐标系轴夹角为

基准尺坐标系中x轴过测站中心平行线在两测站测角仪器中水平角观测值HSA、HSB分别为

通过计算两测站中心在基准尺坐标系中高程，可求得两测站中心高差

2.2 绝对定向

绝对定向是确定工业测量系统的尺度基准，即确定基线的值［4］.采用非互瞄方式完成测站测角仪器中心在基准尺坐标系下坐标定位，即相对定向过程中直接观测作为长度基准的基准尺，无需再对两台或多台观测仪器采用传统方式进行专门的系统绝对定向，进而获取观测目标的相关观测数据.为测站A和测站B，分别观测基准尺上观测点S1和S2时，获得的水平角观测值.可见，测站坐标系x轴在其水平角观测值HA和HB为

3 精度分析

由于对目标观测采用测角前方交会方式，其精度分析与现有工业测量系统相同，因而本研究仅对与交会测站中心A点相关的D1和D2作精度分析.为不影响目标点观测精度，测站点位中误差一般取观测点点位中误差的1/3为限差.但由于观测点位的中误差受设站位置影响，不宜直接作为精度评定因素.现有的工业测量系统多采用基准尺观测解算数据作为定向精度评定依据，因而本研究选用该方式对系统定向进行精度评定.

由于测站中心A点在基准尺坐标系下的高程坐标也由D1和D2推出，因而A点的坐标精度可由D1和D2推得.以测站中心A至基准尺观测点S1水平距离D1为例，若将D1看作仪器对两基准尺观测点S1和S2水平观测角夹角β，以及视线与z轴夹角δ1和δ2的函数，即

4 验证分析

通过对某检校场的观测，对经由非互瞄定向的三维工业测量系统观测，处理后的目标点坐标数据进行精度评定.

与现有三维工业测量系统 (如Leica Axyz测量系统)进行直观精度对比［9］.使用该系统安装有内觇标的TM5100A电子经纬作为验证实验观测仪器，基线长度约9 m，基线距观测目标点间水平距离约为4.5 m.基准尺采用双向符合水准管整平后，在平行于两目标点水平投影方向整平误差小于1.163×10－3mm，垂直于投影方向整平误差小于7.522×10－3mm，对仪器观测精度影响小于0.08″.

通过非互瞄定向方式，完成相关观测，将获取的目标观测数据，经采用光束平差法自行编写的系统观测数据处理软件［10］后，所获得观测目标点在观测坐标系下各方向中误差均方根 (root meansquare，RMS)如表1.

通过分析式 (16)求得mD1，可知测站中心至基准尺观测点S1的水平距离D1的精度，除受到测角精度的影响之外，还取决于空间后方交会的空间图形形状.在实际测量中，应尽量增大仪器对两基准尺观测点S1和S2水平观测角夹角β，以及视线与z轴夹角 δ1和 δ2.

表1 观测目标点中误差的均方根Table 1 RMS of observation target mean square error单位:mm

保证测站不变前提下，采用互瞄定向方式进行系统相对定向后，将之前目标点观测获取的数据，经Leica Axyz系统软件处理可获得观测点位在该系统下的观测坐标系坐标值.由于两组坐标系不同，而坐标转换误差远大于观测误差，无法直接进行精度比较.采用两坐标系下相邻点间距离差值进行间接对比，所得两系统间相邻点间距互差d如表2.

表2 Axyz与NMCO系统间相邻点间距计算Table 2 Comparison of vicinity points distance between Axyz and NMCO systems 单位:mm

由表1和表2的结果可知，基于可整平基准尺的非互瞄工业测量系统中，对目标点的观测中误小于0.03 mm.与Leica Axyz三维工业测量系统相比，相邻点间距互差最大值为0.009 mm.上述观测精度符合工业测量观测精度要求.

结 语

采用TM5100A电子经纬仪和同等观测精度测角仪器 (如同时具备测距功能的TCA2003全站仪)观测验证，基于可整平基准尺的非互瞄观测定向模型与现有Leica Axyz工业测量系统的观测精度相同，并可满足精密工程及设备的工业测量观测要求.由于本研究不需要两台以上观测设备互瞄，在保证可整平基准尺位置不变的前提下，各观测设备与静态观测目标点的观测相互独立，因此可采用一台观测设备通过搬站实现对目标点的观测，降低设备采购成本.通过该定向模型，构建了价格低廉，且测量精度和性能可与国外成熟商品化系统相媲美的新型三维工业测量系统.

/References:

［1］LI Guan-yun.The state of the art and applications of the industrial measuring systems［J］.Engineering of Surveying and Mapping，2001，10(2):36-40.(in Chinese)李广云.工业测量系统最新进展及应用［J］.测绘工程，2001，10(2):36-40.

［2］LI Zong-chun，LI Guang-yun，TANG Ting-song，et al.E-lectronic multi-theodolite measuring system applied in the precision installation of a large antenna［J］.Hydrographic Surveying and Charting，2005，25(1):25-29.(in Chinese)李宗春，李广云，汤廷松，等.电子经纬仪交会测量系统在大型天线精密安装测量中的应用［J］.海洋测绘，2005，25(1):25-29.

［3］FENG Wen-hao，ZHENG Wen-hua.Some methods for orientation of initial direction between two angle-measurement instruments in industrial surveying［J］.Wtusm Bulletin of Science and Technology，2002，27(2):1-3.(in Chinese)冯文灏，郑文华.工业测量中两测角装置间起始方向线的定向方法［J］.测绘信息与工程，2002，27(2):1-3.

［4］FENG Wen-hao.A method to set up control net with extra high accuracy for industrial objects［J］.Journal of Wuhan Technical University of Surveying and Mapping，1999，24(2):119-123.(in Chinese)冯文灏.工业测量中特高精度控制网的建立方法［J］.武汉测绘科技大学学报，1999，24(2):119-123.

［5］FENG Wen-hao.Method for setting up a three-dimensional industrial surveying system of building blocks type［J］.Geomatics and Information Science of Wuhan University，2002，27(4):403-407.(in Chinese)冯文灏.建立积木式三维工业测量系统的研究［J］.武汉大学学报:信息科学版，2002，27(4):403-407.

［6］FENG Wen-hao.Some applications of standard rulers in industrial surveying［J］.Bulletin of Surveying and Mapping，2003(3):40-43.(in Chinese)冯文灏.工业测量中标准尺的几种应用［J］.测绘通报，2003(3):40-43.

［7］HUANG Gui-ping，LI Guang-yun.Study of system orientation and coordinate calculation of IMS［J］.Acta Geodaetica et Cartographic Sinica，2003，32(3):256-260.(in Chinese)黄桂平，李广云.电子经纬仪工业测量系统定向及坐标解算算法研究［J］.测绘学报，2003，32(3):256-260.

［8］Stephen K.Axyz Mathematics for Users［Z］.Switzerland:Leica，2000(1).

［9］Stephen K.Axyz Data Manager Software Reference Manual［Z］.Switzerland:Leica，2000(1).

［10］LI Guang-yun，ZHANG Liang-ju，WEI Jian-dong，et al.The bundle adjustment method and its application in TSST industrial measuring system［J］.Journal of the Pla Institute of Surveying and Mpping，1996，13(2):95-107.(in Chinese)李广云，张良琚，卫建东，等.光束法平差在工业测量系统 TSST中的应用［J］.解放军测绘学院学报，1996，13(2):95-107.