基于改进差别矩阵的增量式属性约简算法

冯少荣，张东站

厦门大学信息科学与技术学院，福建厦门361005

知识约简是粗糙集理论［1］的核心内容之一.在粗糙集理论中，知识约简分为属性约简和属性值约简.随着数据库系统中数据的不断增加，属性约简相对属性值约简更加有效.它大大简化了数据库结构的复杂度，提高了人们对隐含在数据库庞大数据量下的各种信息的认识程度.因此，属性约简成为目前粗糙集的研究热点之一［2-5］.决策表的属性约简通常是不唯一的，人们希望能找到具有最少属性的最佳约简.然而，找到最佳约简是一个NP-hard问题，导致NP-hard的主因是属性的组合爆炸，解决该问题通常采用启发式搜索方法，求出最佳或次最佳约简［6-8］.现有的属性约简大体上可分为，基于差别矩阵或基于差别矩阵的改进的属性约简算法、基于正区域的属性约简算法及启发式的属性约简算法，其共同特点是:①利用属性的重要性作为启发式信息，但并不完备［9］;②这些算法大都针对静态的信息系统或决策表，不适合信息系统或决策表动态变化的情况.现有的有关属性约简的增量式算法不多，已有的动态增量属性约简算法，其时间和空间复杂度都较高.很多属性约简是从求属性核开始的，所以求核是粗糙集理论的关键之一，求解属性核也面临同样问题.

本研究围绕粗糙集中的求属性核和属性约简问题，分析现有的求核算法和属性约简算法［10-11］时间和空间复杂度高的原因，基于差别矩阵对称性，通过改进差别矩阵定义，改进增量式求属性核算法及高效的属性约简完备算法.理论分析和实验验证都表明，本研究提出的算法有效可行，可明显降低时间和空间复杂度.

1 改进的差别矩阵定义及求核算法

1.1 改进的差别矩阵定义

按照文献 ［11］差别矩阵定义，U1为论域，xi和xj是论域U1中的元素，mij和mji是差别矩阵M中的元素项，在计算差别矩阵时，当xi∈U1，xj∈U1时，mij=mji，文献 ［11］ 同时计算了mij及mji.由于差别矩阵是对称的，因此只需计算mij就能正确求核.当较大时，可显著降低计算量，特别是当决策表一致时，减少的不必要计算量是求核实际所需计算量的1/2.

故当xi∈U1，xj∈U1时，通过限定i＞j，只计算mij，而不需计算与其对称且相等的mji.因此，本研究对给定信息系统 (information system，IS)，将文献 ［11］的差别矩阵M={mij}重新定义为

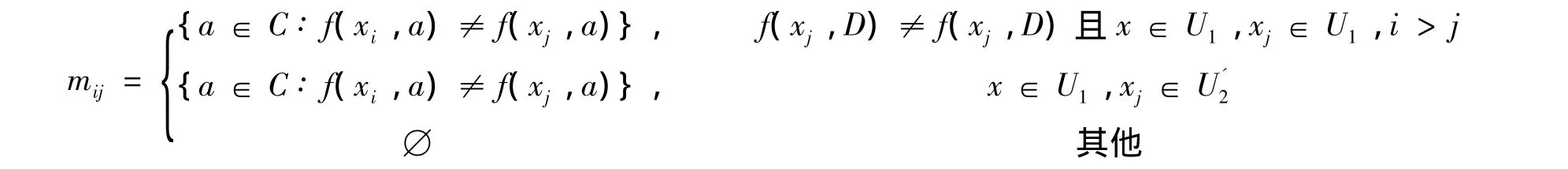
1.2 改进的求核算法

针对动态增加的情况，文献［11］中算法2(optimization for incremental updating algorithm of a core，OIUAC)的时间复杂度为时间复杂度较低.该算法的空间复杂度为 O，由于该算法在计算核时使用了差别矩阵，导致空间复杂度较高，特别当决策一致时，U1=U，U'2=0，U为论域，空间复杂度为，不能有效处理大数据集.为此，本研究通过改进文献［11］中的算法2，由于差别矩阵是对称矩阵，只存储差别矩阵下三角部分，降低空间复杂度.

基于本研究重新定义的差别矩阵，新的求属性核的算法流程如图1.其中，C为条件属性集合;f为属性集到值域集的映射;count(≥1)为mij在差别矩阵M中出现的次数;DMSC(C)为C的核.

2 改进的核增量式算法

2.1 算法原理

在只存储差别矩阵下三角部分情况下，针对文献［11］的3种情况，本研究分别做如下处理:

①当x与(U1∪U'2)一致时，计算x与U1∪U'2间的mij，并按如图2的处理过程，将 mij增至DMSC(C)，U1=U1∪ {x}.

②当x与U1不一致时，在U1中找出与x不一致的 y，计算 y与 U1∪ U'2之间的 mij，并把DMSC(C)中相应的mij依据图2处理过程删除;令U'2=U'2∪{y}，U1=U1－{y}，并计算y与U1之间的mij，按图2处理过程，将mij增至DMSC(C).

③当x与U'2不一致时，DMSC(C)保持不变.

改进的核增量式算法 (improved optimization for incremental updating algorithm of a core，IOIUAC)流程图如图2.其中，core(C)表示最终得到的条件属性集C的核.

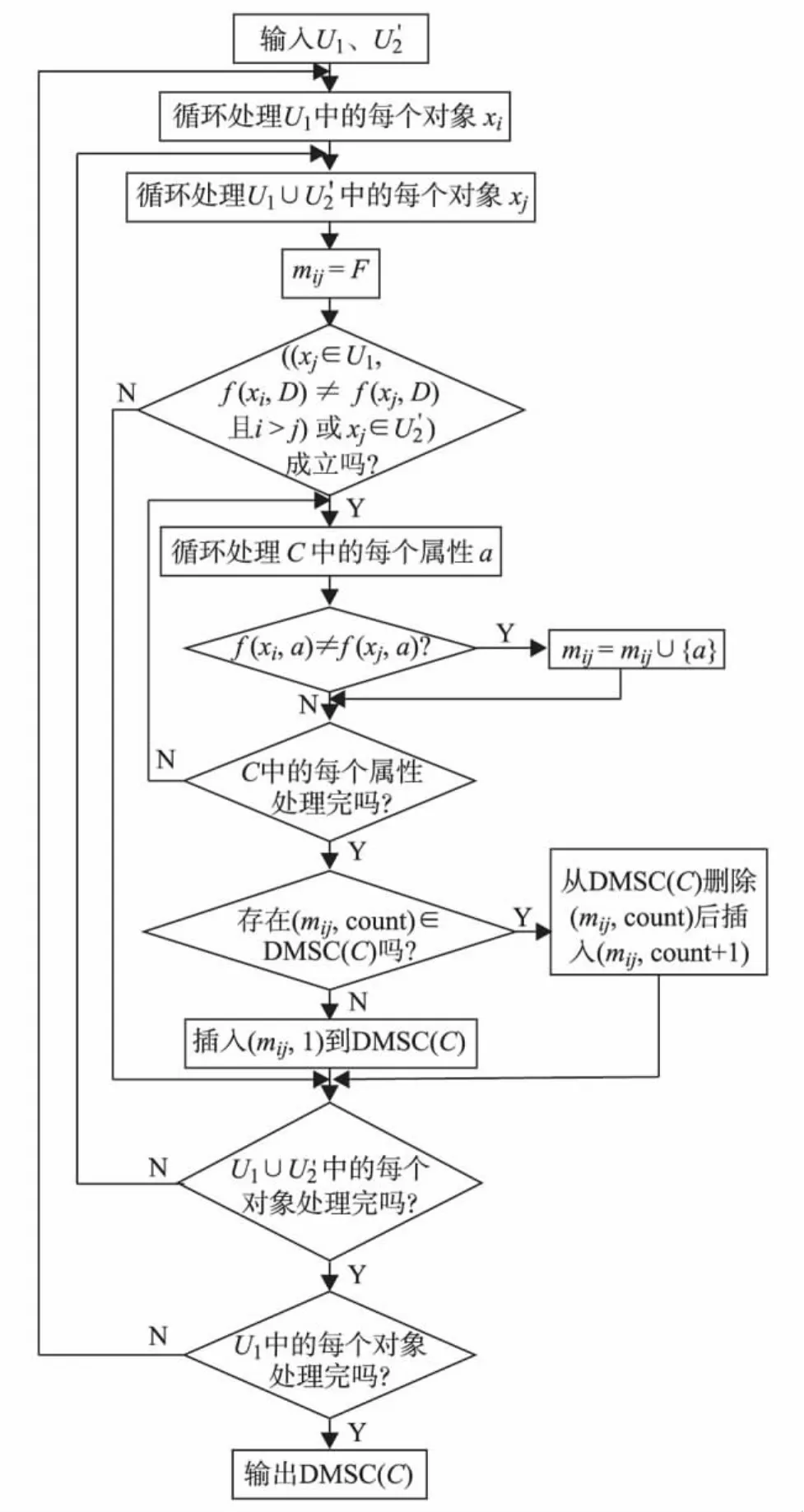
图1 改进的求核算法Fig.1 Improved algorithm of the computation of a core

2.2 算法分析

①当x与(U1∪U'2)一致时，将x加入U1，文献［11］对差别矩阵增加了1行1列，由于mij=mji，当xi∈U1，xj∈U1时，增加的列对于核计算来说是多余的，所以IOIUAC只需计算相应的行;此时计算量为.判断x与(U1∪U'2)是否一致，所需计算量为故在此情况下，IOIUAC的总时间复杂度为

②当x与U1不一致时，计算U1中与x不一致的对象y，并删除DMSC(C)中y所在行的单个属性，其计算量为然后，y作为U'2中的对象计算相应的DMSC(C)，其计算量为判断一致性的时间为，所以，x与U1不一致时总的时间为故IOIUAC的时间复杂度为，小于文献［11］中算法2的时间复杂度

③当x与U'2不一致时，文献［11］算法2空间复杂度为，而算法IOIUAC空间复杂度为为条件属性数.由于，故 IOIUAC较文献［11］中算法2的空间复杂度有显著改善.

2.3 实验

在内存为1 024 MB，CPU为PⅣ 2.9 GHz，操作系统为Windows XP的联想PC上，Eclipse下Java实现文献［11］中算法 OIUAC及本研究提出的IOIUAC.利用UCI提供的蘑菇数据库 (mushroom)进行实验，该数据库有8 124个对象.将蘑菇数据库看作决策表，并进行2个实验.

实验1 从8 124个对象中选择7 000个对象作为基准决策表 (基准决策表即该表生成的差别矩阵作为OIUAC和IOIUAC的输入)，从剩下1 124个对象中依次选择200、500、800和1 124个对象作为增量，执行OIUAC和IOIUAC，运行结果如图3.

实验2 由蘑菇数据库生成8 000个对象，其中有1 000个不一致对象，从生成的8 000个对象中选择7 500条作为基准决策表，从剩下的500个对象中依次选择100、200、300和500个对象作为增量，执行OIUAC和IOIUAC，运行结果如图4.

2.4 实验分析

实验1 8 124个对象为一致性对象.OIUAC计算及遍历差别矩阵相应的行和列，而IOIUAC只需计算1行，又因我们优化了核属性计算算法，所以IOIUAC的计算时间比较少.

实验2 当x与U1不一致时，OIUAC首先遍历差别矩阵中与x相应的行和列，删除DMSC(C)中相关的核属性，然后把该对象插入U2，计算U2中x相应的差别矩阵，把核属性插入DMSC(C).此时，IOIUAC的计算量明显少于OIUAC的计算量.

对实验过程的监测结果显示，OIUAC因为存储差别矩阵，随着对象数从7 200个增至8 124个，内存使用量从225 Mbit增至285 Mbit;而IOIUAC内存使用量一直保持小幅增加，增幅仅约20 M.所以，IOIUAC较OIUAC的另一重要优势为前者可应对大数据集的挑战.

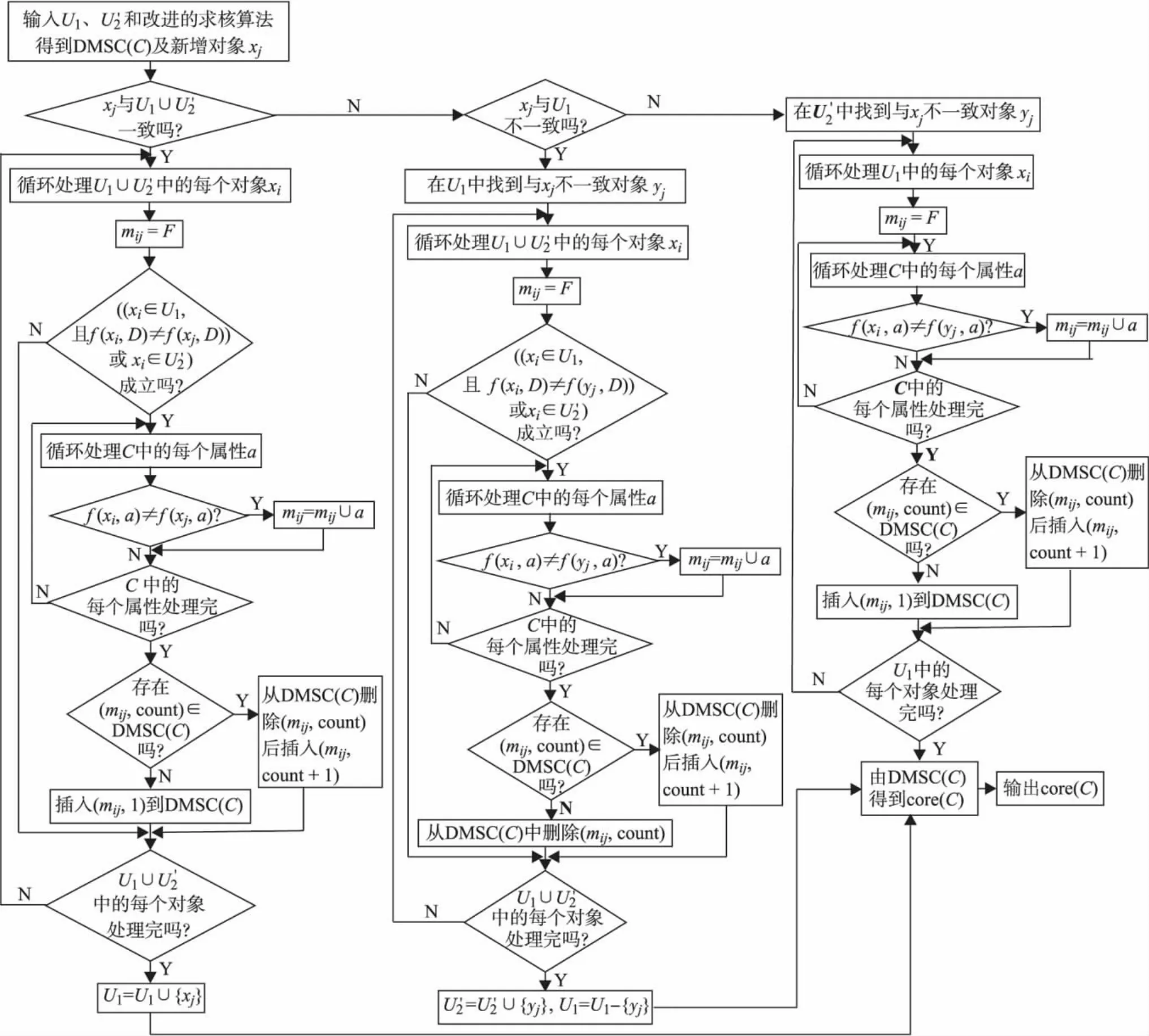
图2 改进的核增量式算法Fig.2 Improved optimization for incremental updating algorithm of a core

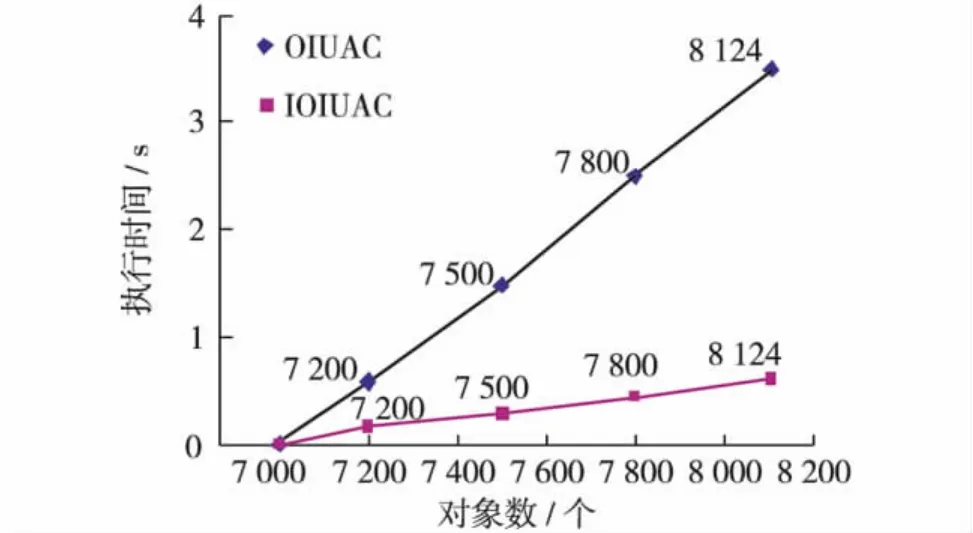
图3 第1组实验算法的执行时间Fig.3 Algorithm running time in first group experiment

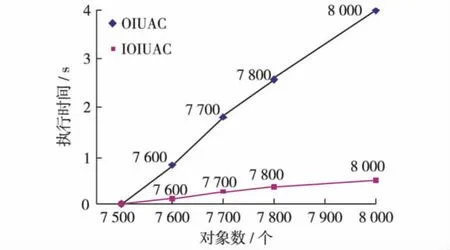
图4 第2组实验算法的执行时间Fig.4 Algorithm running time in second group experiment

3 改进的属性约简完备算法及其分析

文献［12］的增量式属性约简算法多次调用求核过程，其时间复杂度为，这是引起时间复杂度高的一个重要原因;又因该算法存储了差别矩阵，求核遍历差别矩阵的时间复杂度为，故文献［12］使用差别矩阵是引起时间空间复杂度高的另一重要原因.当决策表一致时，有U1=U，文献［12］属性约简算法的时间和空间复杂度至少为O

徐章艳［13］给出的属性约简算法RedueBaseSig，其时间复杂度为，由于该算法未从求核出发，在某些情况下，获得并非属性的约简，其中会包含冗余属性.

文献［14］对RedueBaseSig进行了改进，提出一种基于分布计数的基数排序方法的等价类划分算法.对决策表采用分布计数的基数排序，按属性集C对决策表S排序，该算法的时间复杂度也为O，空间复杂度为

3.1 改进的属性约简完备算法

改进的增量式属性约简算法 (improved incremental updating algorithm of attribute reduction for inserting，IIUAARI)分2种情况:① 新增对象x，若x与U'2一致或x与U'2中的某个对象不一致或x与U1中的对象是P一致的，则P是一个属性约简;②其他情况，由增量式核算法IOIUAC计算得到的核开始重新计算属性约简.

IIUAARI流程如图5.其中，POSC(D)表示D的C正域，POSS(D)表示D的S正域，NEGS(D)表示D的S负域.

3.2 时间复杂度分析

运行IIUAARI算法时各中间步骤的时间复杂度分别为:更新 DMSC(C)为判断一致性为由DMSC(C)得到核为判断P不一致性为计算POSC(D)、POSS(D)和 NEGS(D)时，3个公式的复杂度都为 O;POSC(D)≠POSS(D)的循环处理为综上可知，算法IIUAARI总时间复杂度为

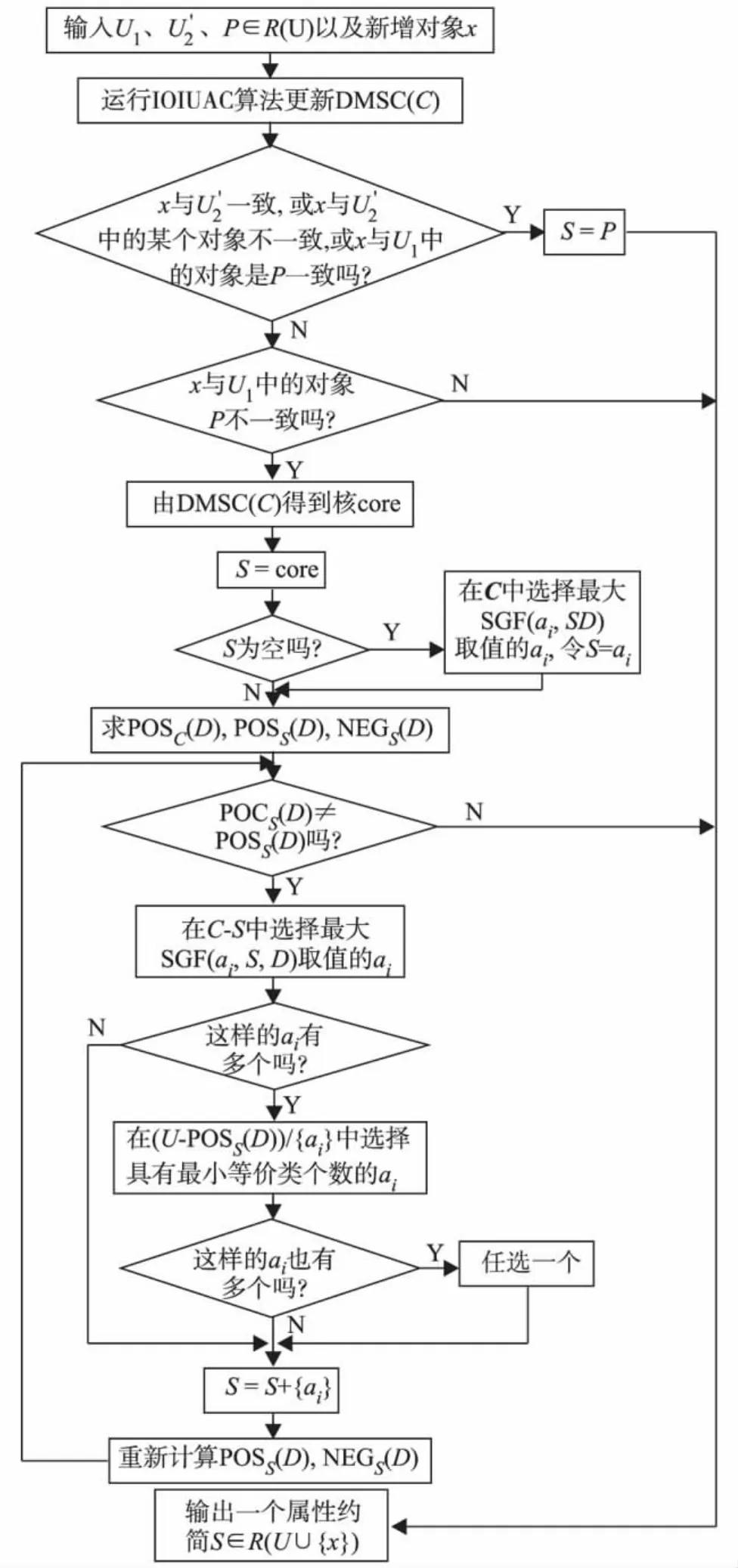
图5 改进的增量式属性约简算法Fig.5 Improved incremental updating algorithm of attribute reduction

由于IIUAARI算法没有存储差别矩阵，所以它的时间复杂度较文献［12，15］的有显著降低，并与文献［14］的时空复杂度相当.但文献［14］的求核算法只能用于求一致性决策表的核;而IIUAARI算法充分利用已有的核，能减少计算量，适用于一致性、不一致性决策表的属性增量式约简;同时当新增对象x，x与U2中的某个对象不一致或x与U1中的对象是P一致时，IIUAARI的时间复杂度为能高效求得属性约简.

3.3 示例说明

表1是一张有5个对象和5个属性二值数据表，其中，C={C1，C2，C3，C4}为条件属性集;D 为决策属性.

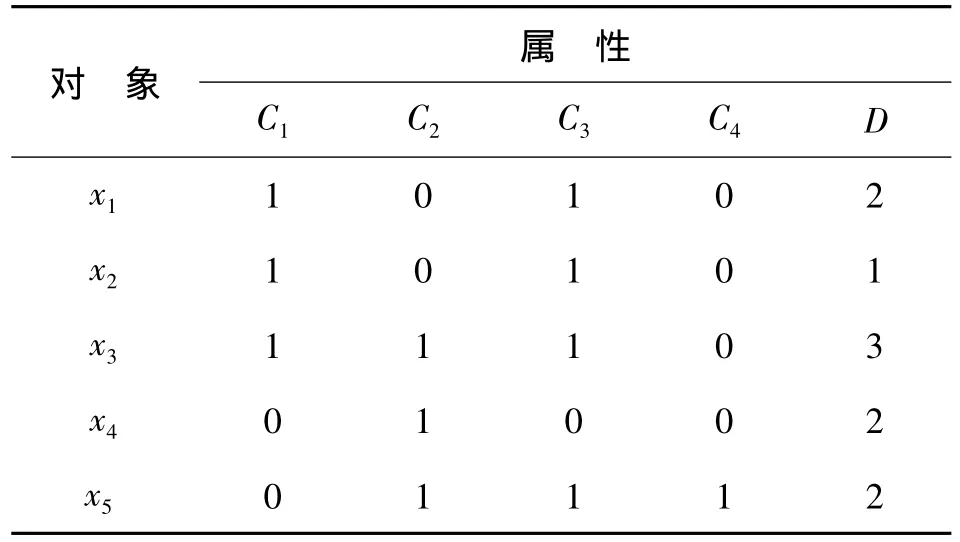
表1 二值数据表Table 1 Two-value data table

由表1可知，U1={x3，x4，x5}，U2={x1，x2}，U'2={x1}，由文献［11］定义可得差别矩阵M为

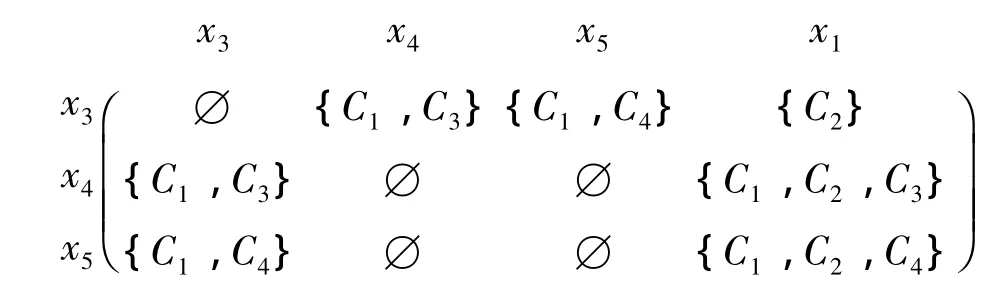
由文献［11］可得，该表中核为{C2}.由文献［1］可知，{C1，C2}和{C2，C3，C4}为其2个属性约简.

为进一步说明算法IIUAARI，以下通过新增对象x说明插入对象后属性约简更新情况.

① 若 x={1，0，1，0，3}，则 x与 x1不一致，由IIUAARI可知，核和属性约简不变.

② 若 x={1，1，1，0，1}，则 x与 x3不一致;当IIUAARI通过IOIUAC更新DMSC(C)，且x与U1中的对象不一致时，由DMSC(C)=∅及S=∅，可得 SGF(C1，S，D)=2/6， SGF(C2，S，D)=0，SGF(C3，S，D)=1/6，SGF(C4，S，D)=1/6;在C中选择 C1，使得 SGF(ai，S，D)取值最大，则 S={C1}，由于POSC(D)=POSS(D)，故S={C1}为一属性约简.

③ 若 x={0，1，0，0，3}，则 x与 x4不一致;当IIUAARI通过IOIUAC更新DMSC(C)，且x与U1中的对象不一致时，由 DMSC(C)={C2}及 S={C2}，可得SGF(C1，S，D)=1/6，SGF(C3，S，D)=0，SGF(C4，S，D)=1/6;(U-POSS(D))/{C1}=2，将C1加入 S，得 S={C1，C2};重新计算可得SGF(C3，S，D)=1/6， SGF(C4，S， D)=1/6;(U-POSS(D))/{C1}=2，将 C3加入 S，S={C1，C2，C3}，此时 POSC(D)=POSS(D)，故 S={C1，C2，C3}为一属性约简.

④ 若 x={1，1，0，1，3}，则 x 与原决策表中的对象P一致，由算法IIUAARI可知，核和属性约简不改变.

⑤ 若 x={0，1，0，1，3}，则 x 与原决策表中的对象一致;IIUAARI通过IOIUAC更新DMSC(C);由 DMSC(C)={C2，C3，C4}，S={C2，C3，C4}，POSC(D)=POSS(D)，可得 S={C2，C3，C4}为一属性约简.

可见算法IIUAARI在各种情况下得到的约简与文献［12］算法相同，本文示例取自文献［12］.

结 语

本研究基于已有增量式求核算法，提出不存储差别矩阵的改进增量式求核算法，由于差别矩阵是对称矩阵，本研究中的求核算法，通过只存储差别矩阵下三角部分，有效降低了空间复杂度.故能有效地处理大数据集.由于本文的IIUAARI算法没有存储差别矩阵，充分利用已有的核，显著减少计算量，降低了属性约简的复杂度，较已有的属性约简增量式算法［12-18］更高效，而且它适用于一致性、不一致性决策表的属性增量式约简.故可以用于快速处理大数据集，能高效的求得属性约简.

下一步我们将继续完善属性约简算法，着重考虑对象删除情况下核增量式算法及属性约简的更新问题.

/References:

［1］ Pawlak Z.Rough sets［J］.International Journal of Information and Computer Science，1982，11(5):341-356.

［2］ QIAN Yu-hua，LIANG Ji-ye，Pedrycz Witold，et al.Positive approximation:an accelerator for attribute reduction in rough set theory ［J］.Artificial Intelligence，2010，174(9/10):597-618.

［3］ HE Qiang，WU Cong-xin，CHEN De-gang，et al.Fuzzy rough set based attribute reduction for information systems with fuzzy decisions ［J］.Knowledge-Based Systems，2011，24(5):689-696.

［4］ QIAN Yu-hua，LIANG Ji-ye，Pedrycz Witold，et al.An efficient accelerator for attribute reduction from incomplete data in rough set framework ［J］.Pattern Recognition，2011，44(8):1658-1670.

［5］ XU Wei-hua，LI Yuan，LIAO Xiu-wu.Approaches to attribute reductions based on rough set and matrix computation in inconsistent ordered information systems ［J］.Knowledge-Based Systems，2012，27:78-91.

［6］ Wong S K M，Ziarko W.On optimal decision rules in decision tables［J］.Bulletin of Polish Academy of Sciences，1985，33(11/12):663-676.

［7］ Hu X H，Cercone N.Mining knowledge rules from databases:a rough set approach［C］//Proceedings of the 12th International Conference on Data Engineering.New Orleans(USA):IEEE Press，1996:96-105.

［8］ Hu X H，Nick Cercone.Learning in relational databases:a rough set approach ［J］.International Journal of Computational Intelligence，1995，11(2):323-338.

［9］ WANG Guo-yin，YU Hong，YANG Da-chun.Decision table reduction based on conditional information entropy［J］.Chinese Journal of Computers，2002，25(7):759-766.(in Chinese)王国胤，于 洪，杨大春.基于条件信息熵的决策表约简 ［J］.计算机学报，2002，25(7):759-766.

［10］ YE Dong-yi，CHEN Zhao-jiong.A new discernibility matrix and the computation of a core［J］.ACTA Electronica Sinica，2002，30(7):1086-1088.(in Chinese)叶东毅，陈昭炯.一个新的差别矩阵及其求核方法［J］.电子学报，2002，30(7):1086-1088.

［11］ YANG Ming.An incremental updating algorithm of the computation of a core based on the improved discernibility matrix ［J］.Chinese Journal of Computers，2006，29(3):407-413.(in Chinese)杨 明.一种基于改进差别矩阵的核增量式更新算法［J］.计算机学报，2006，29(3):407-413.

［12］ YANG Ming.An incremental updating algorithm for attribute reduction based on improved discernibility matrix［J］.Chinese Journal of Computers，2007，30(5):815-822.(in Chinese)杨 明.一种基于改进差别矩阵的属性约简增量式更新算法 ［J］.计算机学报，2007，30(5):815-822.

［13］ XU Zhang-yan，YANG Bin-ru.Quickly attribution reduction algorithm based on decision table［J］.Journal of Chinese Computer Systems，2006，25(5):858-861.(in Chinese)徐章艳，杨炳儒.一个基于决策表的快速属性约简算法 ［J］.小型微型计算机系统，2006，25(5):858-861.

［14］ GE Hao，LI Long-shu，YANG Chuan-jian.Improvement to quick attribution reduction algorithm ［J］.Journal of Chinese Computer Systems，2009，30(2):308-312.(in Chinese)葛 浩，李龙澍，杨传健.改进的快速属性约简算法［J］.小型微型计算机系统，2009，30(2):308-312.

［15］ LIU Yang，FENG Bo-qin，ZHOU Jiang-wei.Complete algorithm of increment for attribute reduction based on discernibility matrix［J］.Journal of Xi'an Jiaotong University，2007，41(2):158-161.(in Chinese)刘 洋，冯博琴，周江卫.基于差别矩阵的增量式属性约简完备算法 ［J］.西安交通大学学报，2007，41(2):158-161.

［16］ QIAN Jin，YE Fei-Yue，LU Ping.An incremental attribute reduction algorithm in decision table［C］//Proceedings of the Seventh International Conference on Fuzzy Systems and Knowledge Discovery(FSKD).Yantai(China):IEEE Press，2010，4:1848-1852.

［17］ XU Yi-tian，WANG Lai-sheng，ZHANG Rui-yan.A dynamic attribute reduction algorithm based on 0-1 integer programming ［J］.Knowledge-Based Systems，2011，24(8):1341-1347.

［18］ ZHANG Jun-bo，LI Tian-rui，RUAN Da.Rough sets based incremental rule acquisition in set-valued information systems［J］.Autonomous Systems:Developments and Trends，2012，391:135-146.