几种面向弹道目标跟踪算法的性能评估

王 品，谢维信，刘宗香，李鹏飞

1)深圳大学ATR国防科技重点实验室，深圳518060;2)防空兵指挥学院导弹系，郑州450052

目前预警系统的任务之一就是跟踪战略导弹，在导弹系数未知的情况下选择合适的滤波器至关重要.随着非线性滤波方法和机动目标跟踪方法的发展，弹道导弹目标的滤波跟踪方法和跟踪精度都得到不断改善［1-2］，伴随高速计算机的发展，卡尔曼滤波器在复杂的实时应用中也得以实现.近年来，多种非线性卡尔曼滤波已被广泛用于视频和激光跟踪系统、卫星导航、战略导弹轨迹估计、雷达等控制系统［1-6］.然而，在工程应用中面临的问题是多样的，对滤波器性能的要求也不一样.可以说，滤波器性能决定着信息融合系统的整体性能.所以对非线性卡尔曼滤波器的性能做深入研究具有重要现实意义［7-12］.弹道目标从发射到击中目标，经历推进段、自由飞行段和再入段3个飞行阶段［13］.再入段即目标进入大气层的飞行阶段，是本研究的重点.在该阶段，目标受重力、空气阻力等力的影响，由于阻力的非线性导致目标运动也具有很强的非线性特征.因此，采用弹道目标模型检验非线性滤波器的跟踪性能，其结果能充分反映各种非线性滤波器的性能优劣.

本研究在导弹系数未知的情况下，通过分析二维空间弹道目标动力学模型，用Cramer-Rao下界理论推导并分析该模型相应的Cramer-Rao下界，提出相应的评估方法，为非线性卡尔曼滤波器的性能评估提供了理论参考.

1 二维空间中的弹道目标动力学模型

二维空间弹道目标动力学模型的运动方程［1］为

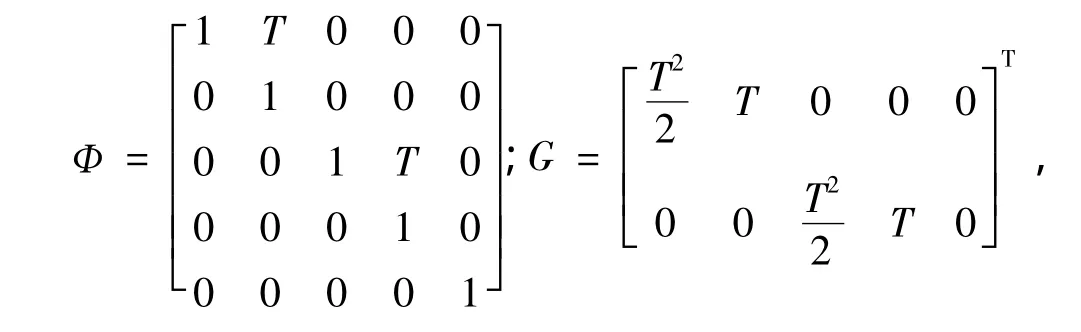
T为雷达采样间隔.过程噪声wk是零均值高斯白噪声，其协方差为

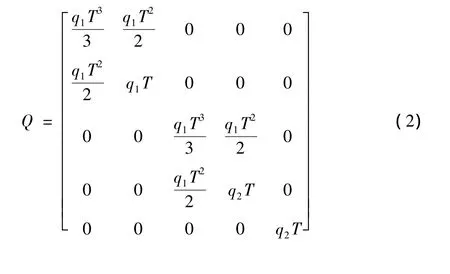
其中，q1和q2为与过程噪声有关的参数.由于阻力加速度的密度函数［1］为 0.5(g/β)ρv2，所以二维空间下空气阻力加速度fk(xk)用目标状态向量的各分量表示为

其中，ρ为空气密度;g为重力加速度;β为弹道系数.

用雷达跟踪目标，雷达坐标为(0，0).斜距离r和高低角ε的误差标准差分别用σr和σε表示.将雷达测量转换为笛卡尔坐标下的参数，测量方程可写成线性形式

其中，zk= ［dkhk］T，d=rcos ε，h=rsin ε;

假设量测噪声vk为零均值高斯白噪声，其协方差为

其中，

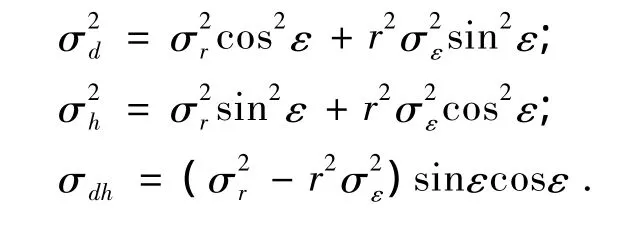
2 弹道目标跟踪的Cramer-Rao下界

由于最优贝叶斯非线性滤波器是无法实现的，因此提出了很多近似的次优算法，而对这些次优算法性能的评估，需有一个理论上的最优性能下界，即Cramer-Rao lower bounds(CRLB).它是一个滤波器性能分析的基准，有重要的应用价值.本研究推导了二维空间弹道目标跟踪的CRLB，并以此为标准比较4种滤波器的跟踪性能.

考虑式 (1)描述的非线性系统，设k时刻的测量集为Zk={zi}ki=1，状态xk的无偏估计为，其协方差为Pk|k，该矩阵的下界记为CRLB，且满足

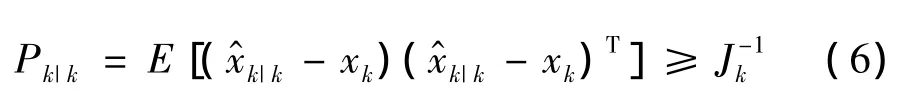
其中，Jk=E{▽skψTk(xk)}T为信息矩阵，其迭代公式为

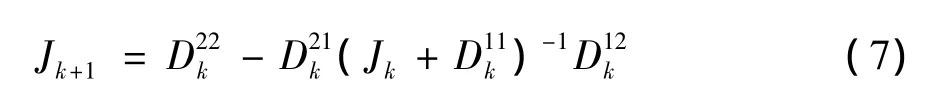
由于过程噪声和测量噪声均为加性高斯噪声，故有

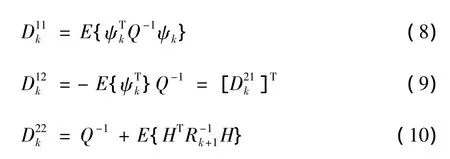
其中，雅克比矩阵

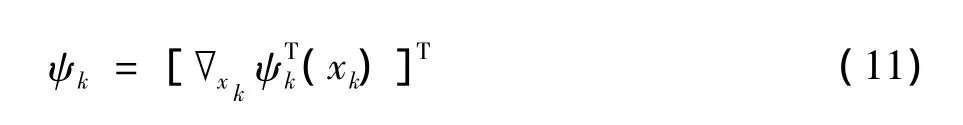
将式 (8)～式 (10)代入式 (7)得

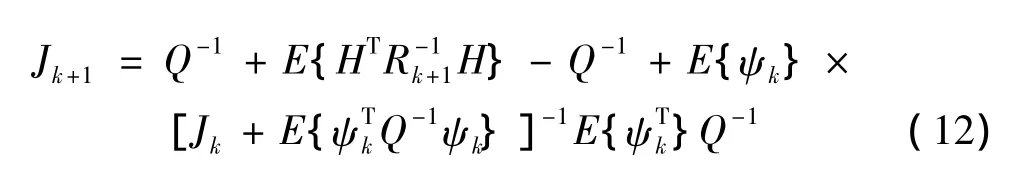
因此，在k时刻，状态向量无偏估计的CRLB为

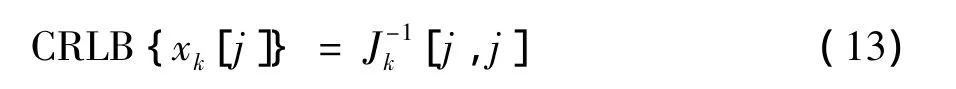
其中，j=1，2，3，4.

若不考虑过程噪声，则信息矩阵的迭代方程［2］为

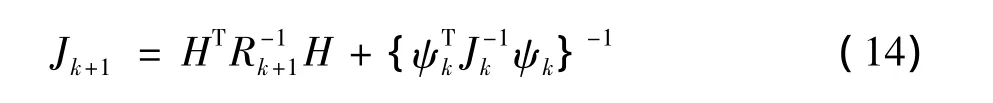
初始信息矩阵J0为初始状态协方差矩阵的逆

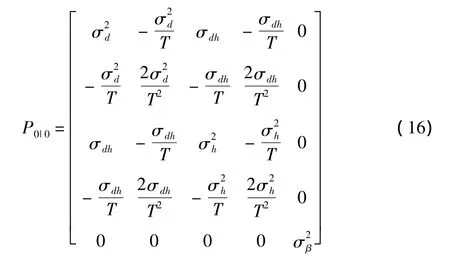
其中，σβ为弹道系数标准差.由式(11)和式(1)得雅克比矩阵

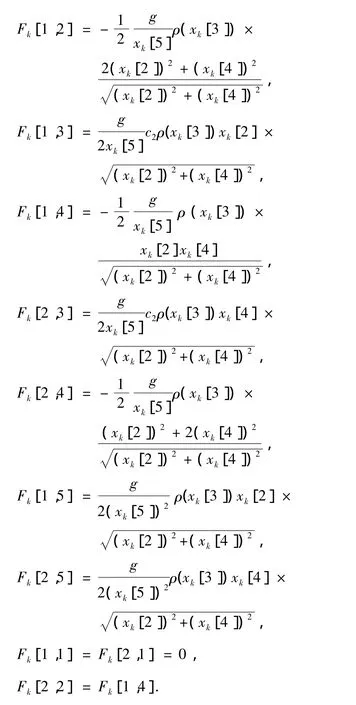
空气密度估计值为 ρ(xk［3］ =c1e-c2xk［3］).

3 非线性Kalman滤波器

3.1 扩展Kalman滤波

扩展 Kalman滤波 (extended Kalman filter，EKF)的基本思想，是将式 (1)的非线性函数通过泰勒级数展开以进行线性化，然后套用线性滤波理论得到求解原非线性滤波问题.其一阶泰勒级数展开式为

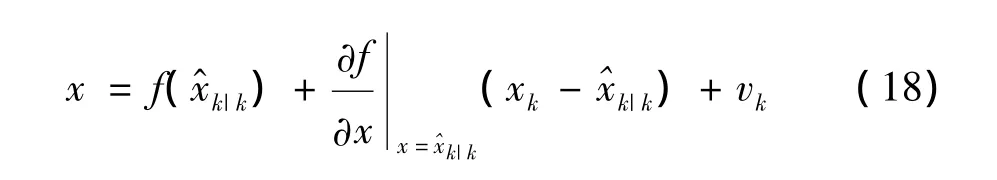
由于忽略了高阶项，EKF具有运算复杂度小，计算效率高等优点，但EKF的非线性变换方式存在较大误差，当维数较大时其雅可比矩阵的计算复杂，有时甚至不存在［8-9］.

3.2 其他典型非线性Kalman滤波器

由于用有限的参数来近似随机变量的概率统计特性要比近似任意非线性函数更容易，因此使用采样方法近似非线性函数的概率分布来解决非线性问题成为近期研究非线性滤波的主要方向.其中，具有代表性的滤波器为基于无迹变换的无迹卡尔曼滤波 (unscented Kalman filter，UKF)、基于 Gauss-Hermite数值积分的积分卡尔曼滤波 (quadrature Kalman filter，QKF)及基于曲面径向体积准则的体积卡尔曼滤波 (cubature Kalman filters，CKF).这3种滤波器均选取一些能体现高斯密度的真实均值和协方差的采样点，将这些点经非线性系统传递的方法拟合高斯密度，经过非线性系统传递后得到的后验均值和协方差都能够精确到二阶以上.由于不需对非线性系统进行线性化，且易于在非线性系统的状态估计中应用，因此UKF、QKF和CKF应用广泛.

3.2.1 UKF

UKF不需对非线性状态和测量模型进行线性化，而是对状态向量的概率密度函数 (probability density function，PDF)进行近似化.近似化后的PDF仍是高斯的，它表现为一系列选取好的δ采用点，对于n维状态，每次循环需2n+1个采样点.采样点和各采样点对应的权值计算参见文献 ［10］.

3.2.2 QKF

QKF是基于Gauss-Hermite数值积分的非线性卡尔曼滤波.通过线性回归点 (Gauss-Hermite积分点)，可确定高斯密度.设状态的后验概率可用高斯分布近似，通过Gauss-Hermite积分点线性回归系统的状态方程和观测方程，可得到系统的先验和后验概率估计.对于n维状态，利用3点Gauss-Hermite积分，每次循环采样点的个数是3n.积分点ξi和相应的权值ωi的计算运用了正交多项式和3对角矩阵之间的关系，用文献 ［11］的方法计算采样点和各采样点对应的权值.

3.2.3 CKF

CKF算法是近年提出的研究高斯分布下的非线性滤波问题［12］的算法，它把高斯分布下的非线性滤波问题归结为积分计算问题，其中被积函数都是非线性函数与高斯密度乘积的形式，然后基于曲面径向体积准则来实现非线性滤波，对于n维状态，利用3阶球面－径向规则，每次循环需要2n个容积点.

3.3 计算复杂度分析

算法复杂度是衡量算法是否具有实时处理能力的指标，在实时性要求很高的系统中显得尤为重要.复杂度只代表各种算法运行1次所需的乘法次数，不包括目标产生、运动和测量时间.设n为状态向量的维数，m为量测向量的维数，实际中m＜n.对同一模型，上述4种滤波器有量的比例关系.假设一阶EKF状态1步预测和1步量测预测分别需A次乘法和B次乘法，预测和更新步EKF相当于只需1个点的计算，而UKF、QKF和CKF的采样点数由状态向量的维数决定，UKF每次递推需2n+1个采样点，1步预测和1步更新约需2n+1×(A+B)次乘法，同样CKF的1步预测和1步更新约需2n×(A+B)次乘法，QKF的1步预测和1步更新约需3n×(A+B)次乘法.

EKF首先要计算雅可比矩阵，通常需计算n2+mn次导数.EKF每次递推过程需1次m×m矩阵求逆运算，约需2m3次乘法运算，再加上计算协方差矩阵及状态更新，所以EKF递推1步约需A+B+2n3+2n2+3mn2+3m2n+2mn+2m3次乘法运算，对于本研究的跟踪模型，A+B=n2+2n+mn，所以EKF的时间复杂度T(n)=O(n3).

UKF、QKF和CKF每次递推都需进行1次m×m矩阵求逆，2次求n×n矩阵的平方根等，每次矩阵求平方根或矩阵分解约需计算2n3次乘法运算.综上可见，UKF和CKF算法的时间复杂度数量级相同，CKF所需采样点数比 UKF少1个，所以CKF的计算量稍小.QKF需3n个采样点，QKF算法的时间复杂度属于其他数量级，所以理论上QKF运行速度最慢.对于本研究的跟踪模型，4种算法相应的计算复杂度如表1.

表1 4种滤波器的复杂度比较Table 1 The complexity of the filters

4 仿真结果及分析

二维弹道目标的状态向量由式 (2)给出，目标的位置和速度的初始值均服从高斯分布.弹道系数的分布并非服从高斯分布，根据目标质量以及截面积的先验知识，可以给出弹道系数的取值区间β0∈［βL，βU］，在该区间上，β0服从β分布［2］，其概率密度函数

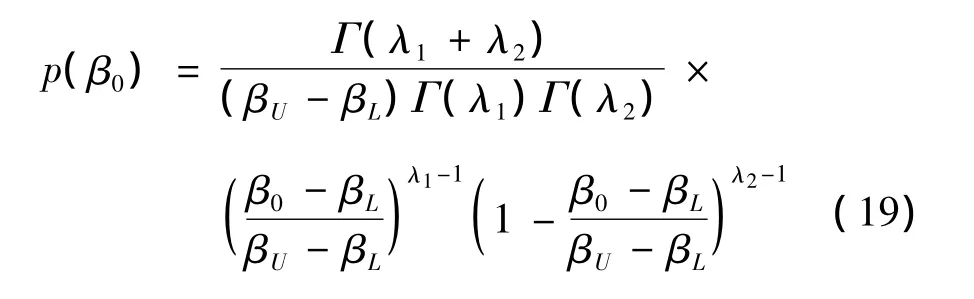
其中，λ1和λ2的取值决定概率密度函数的形状;Γ为Gamma函数.仿真实验中，上述4种非线性滤波器均要求待估计量的概率密度函数服从高斯分布，初始状态向量服从N(，P0|0)，因此我们需要用高斯密度函数来近似p(β0)［2］，如图1.

实验中弹道系数的参数设置为:λ1=λ2=1.9，βL=1 ×104kg/ms2，βU=6.3 ×104kg/ms2，用于近似β分布的高斯概率密度函数的均值和标准差分别为36 500 kg/ms2和14 500 kg/ms2.雷达测量距离标准差为σr=200 m，测量方位角标准差为σε=0.017 rad，4种非线性滤波器的采样时间间隔T=0.1 s，采样次数N=300，噪声参数q1=q2=5，g=9.81 m/s2.采用500次蒙特卡罗仿真，初始速度v0=2 290 m/s，目标初始方向γ0=19π/18，所以初始状态 x0=［232000 v0cosγ0130000 v0sinγ040000］T，用平均误差、均方根误差及CRLB理论来检验滤波性能，结果如图2～图5.图2是4种滤波器跟踪弹道目标的位置估计均方根误差，从图2可见，QKF、UKF和CKF跟踪精度明显优于EKF，且CKF的均方根误差变化相对平稳.图3～图5是500次仿真实验4种滤波器对目标位置、速度和弹道系数估计的平均误差，图中显示在25 s前后，EKF在估计目标位置、速度和弹道系数上均开始产生很大偏差，并在后来产生不同程度的发散.CKF跟踪精度最好，QKF、UKF和CKF跟踪精度相差不大，估计精度几乎接近CRLB，接近最优.

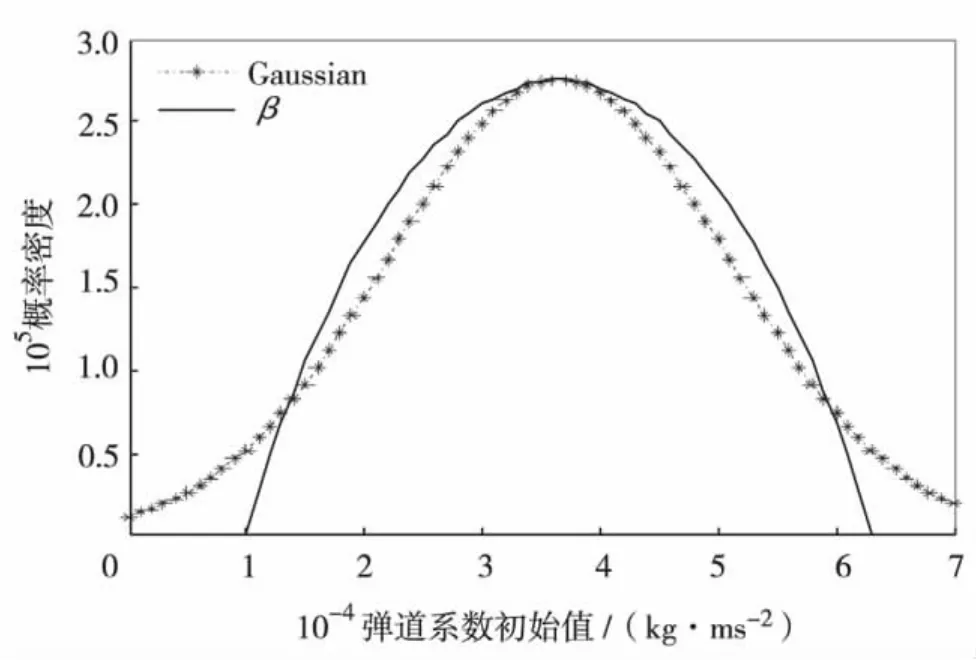
图1 弹道系数初始值概率密度函数Fig.1 Probability density of ballistic coefficient

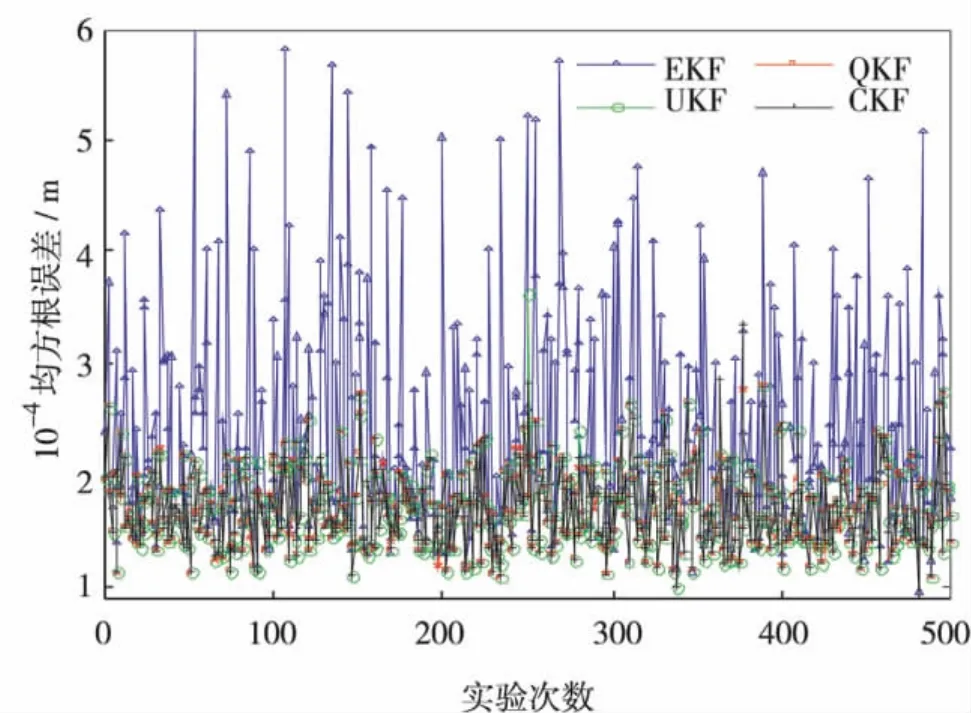
图2 500次实验均方根误差比较Fig.2 The comparison of the RMSE in 500 times

原因是EKF仅仅利用了非线性函数Taylor展开式的一阶偏导部分 (忽略高阶项)，它是对非线性系统模型进行的线性化近似，进而利用KF算法进行滤波估计，本研究采用的二维弹道模型弹道系数是变化的，目标的加速度也是变化的，所以机动性很强，导致估计EKF的状态后验分布时产生较大误差，影响滤波算法的性能，从而影响整个跟踪系统的性能.QKF、UKF和CKF是对状态的概率统计近似，即设计少量的采样点，这些采样点经过非线性函数的传播，计算向量的统计特性，所以估计精度更高.

表2比较了4种非线性滤波器500次实验的平均运行时间.由表2可知，EKF的跟踪实时性能最好，QKF跟踪实时性能最差，QKF的平均运行时间是EKF的89倍.因在本研究的实验中，状态向量是5维的，量测向量是2维的，由表l中的复杂度分析可知，经过300次采样，EKF的乘法次数约为17.7×104次，UKF的乘法次数约为54.8×104次，CKF的乘法次数约为48.6×104次，QKF的乘法次数约为748.2×104次.

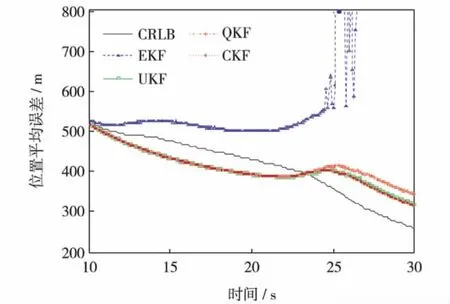
图3 位置平均误差和CRLB的比较Fig.3 Mean estimation error of position versus CRLB

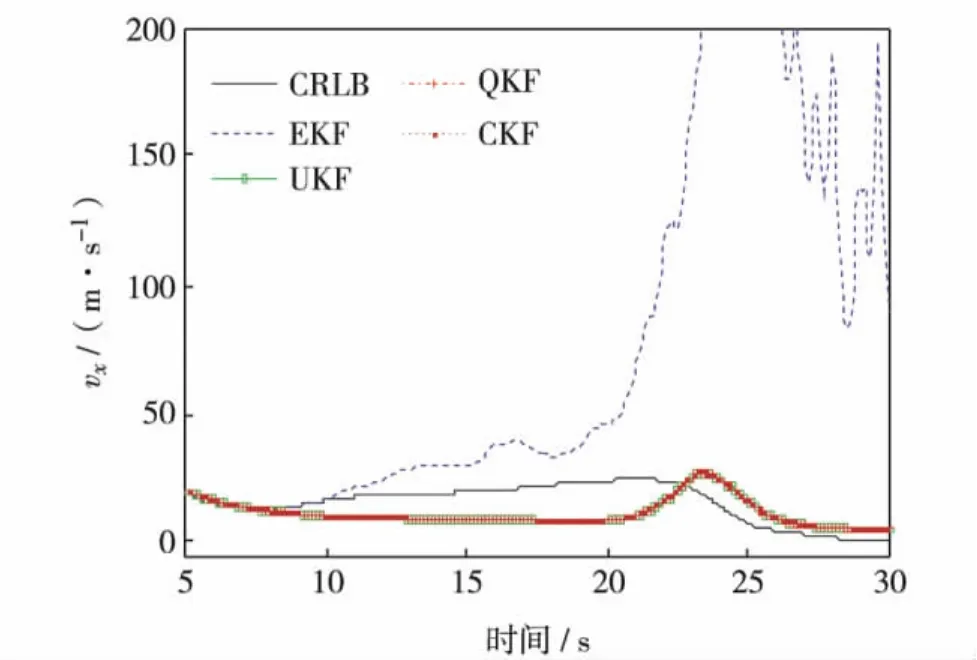
图4 速度平均误差和CRLB的比较Fig.4 Mean estimation error of velocity versus CRLB

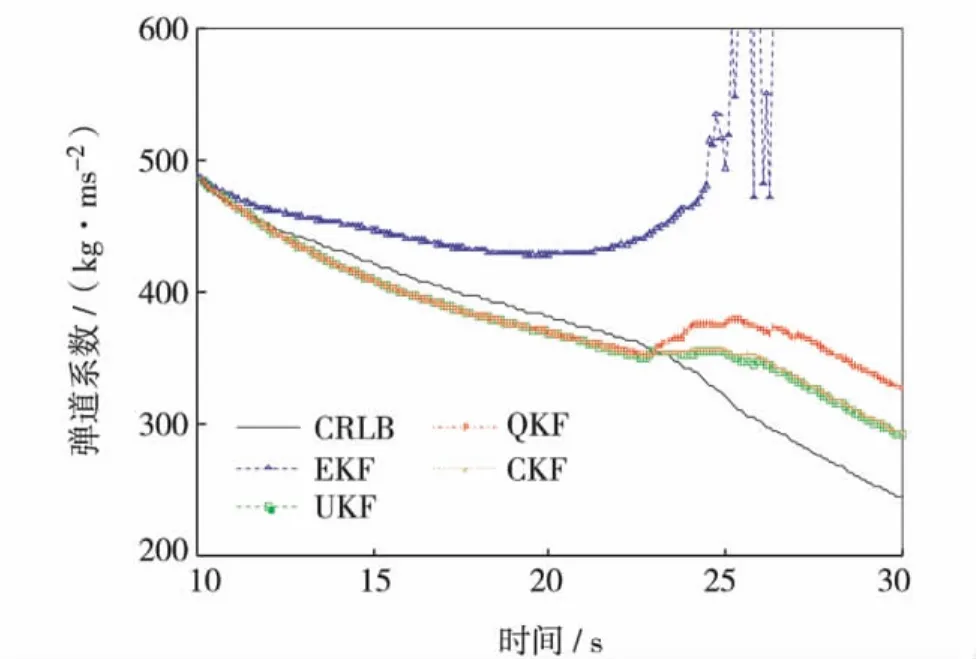
图5 弹道系数平均误差和CRLB的比较Fig.5 Mean estimation error of ballistic coefficient

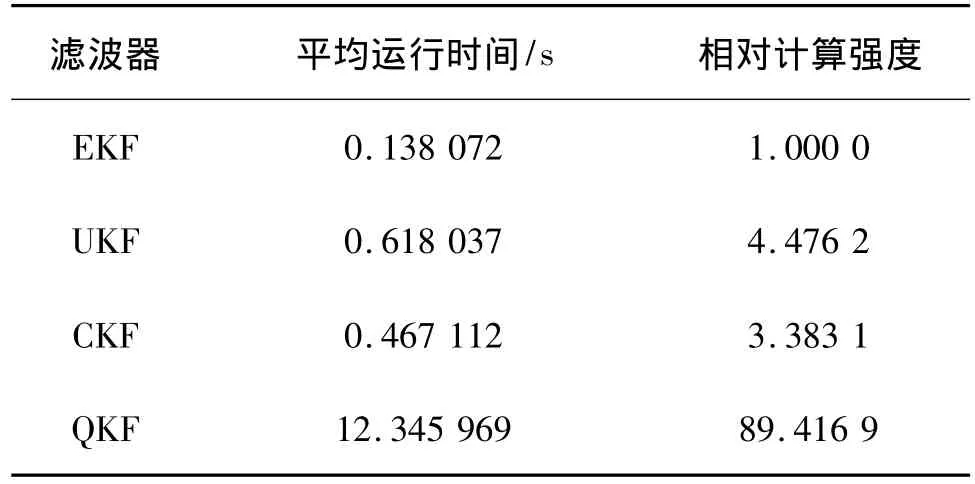
表2 500次试验滤波器的CPU平均运行时间Table 2 The average CPU time of the filters for 500 experiments

结 语

选择合适的滤波器是工程应用的关键之一，可以说滤波技术性能，决定着信息融合系统的整体性能.本研究结合防空作战的需要，在导弹系数未知的情况下利用二维空间中的弹道目标动力学模型，推导该模型的Cramer-Rao下界，基于Cramer-Rao下界理论比较了几种非线性卡尔曼滤波器的性能.综上理论分析和仿真实验结果表明，CKF的跟踪精度较高，跟踪速度相对较快.但针对具体应用环境又表现出各具特色:① 在任何情况下，EKF的跟踪实时性能最好，但跟踪精度最低，因而EKF适用于对跟踪实时性要求较高，对精度要求较低的环境;②QKF的跟踪精度与UKF以及CKF相当，但由于其计算复杂度随状态向量的维数成指数增长，因而不适合工程应用;③ CKF和UKF相比，CKF速度稍微快一点并且相对稳定，此时选择CKF更加合适.这对于提高我国国土防空的侦察预警能力具有重要的现实意义.

/References:

［1］ Farina A，Ristic B，Benvenuti D.Tracking a ballistic target:comparison of several nonlinear filters［J］.IEEE Transactions on Aerospace and Electronic Systems，2002，38(3):854-867.

［2］ Ristic B，Farina A，Benvenuti D，et al.Performance bounds and comparison of nonlinear filters for tracking a ballistic object on re-entry［J］.IEE Proceedings:Radar，Sonar and Navigation，2003，150(2):65-70.

［3］ LI Liang-qun，HUANG Jing-xiong，XIE Wei-xin.Target tracking based on particle filtering in passive sensor array［J］.Journal of Electronics ＆ Information Technology，2009，31(4):844-847.(in Chinese)李良群，黄敬雄，谢维信.被动传感器阵列中基于粒子滤波的目标跟踪［J］.电子与信息学报，2009，31(4):844-847.

［4］ HUANG Jian-jun，LI Peng-fei，YU Jian-ping，et al.Multitarget data association algorithm using cluster cloud model based c-means clustering［J］.Journal of Shenzhen University Science and Engineering，2010，27(1):11-15.(in Chinese)黄建军，李鹏飞，喻建平，等.基于类云模型聚类的多目标数据关联算法 ［J］.深圳大学学报理工版，2010，27(1):11-15.

［5］ GUO Zun-hua，XIE Wei-xin，HUANG Jing-xiong.Performance analysis of sensors transmitting data with wired access scheme［J］.Journal of Shenzhen University Science and Engineering，2010，27(1):1-5. (in Chinese)郭尊华，谢维信，黄敬雄.传感器网络有线接入信息传输性能分析［J］.深圳大学学报理工版，2010，27(1):1-5.

［6］ WAN Jiu-qing，LIANG Xu，MA Zhi-feng.Infrared maneuvering target tracking based on IMM-PF with adaptive observation model［J］.Acta Electronica Sinica，2011，39(3):602-608.(in Chinese)万九卿，梁 旭，马志峰.基于自适应观测模型交互多模型粒子滤波的红外机动目标跟踪 ［J］.电子学报，2011，39(3):602-608.

［7］ Ienkaran Arasaratnam，Simon Haykin.Cubature Kalman smoothers［J］.Automatica，2011，47:2245-2250.

［8］ GAO Song，PAN Quan，XIAO Qin-kun.Maneuvering target tracking based on extended Kalman filter［J］.Fire Control＆ Command Control，2009，34(9):13-17.(in Chinese)高 嵩，潘 泉，肖秦琨.基于扩展卡尔曼滤波的机动目标航迹跟踪 ［J］.火力与指挥控制，2009，34(9):13-17.

［9］ Bar-shalom Y，Li X R，Kirubarajan T.Estimation with Applications to Tracking and Navigation［M］.John Wiley ＆ Sons，2001.

［10］ Julier S，Uhlmann J，Durrant-white H F.A new method for nonlinear transformation of means and covariances in filters and estimators［J］.IEEE Transactions on Automatic Control，2000，45(3):477-482.

［11］ Arasaratnam I，Haykin S，Elliott R J.Discrete-time nonlinear filtering algorithms using Gauss-Hermite quadrature［J］ //Proceeding of the IEEE，2007，95(5):953-977.

［12］ Arasaratnam I，Haykin S.Cubature Kalman filters ［J］.IEEE Transactions on Automatic Control，2009，54(6):1254-1269.

［13］ QI Zhao-hui，LIU Xue-mei，LIANG Wei.Survival simulation and sensitivity analysis of ballistic missile in boost phase based on MCMC ［J］.Systems Engineering and E-lectronics，2010，32(4):803-806.(in Chinese)齐照辉，刘雪梅，梁 伟.基于MCMC的导弹主动段突防仿真及灵敏度分析 ［J］.系统工程与电子技术，2010，32(4):803-806.