基于差分进化算法的认知无线电决策引擎
毕晓君,李安宁
(哈尔滨工程大学信息与通信工程学院,黑龙江哈尔滨150001)
近年来,认知无线电被认为是克服频谱资源紧缺和提高通信效率最具有前景的技术[1],其中认知能力和重配置能力是认知无线电系统必须具备的两大基本功能[2].而认知决策引擎是实现重配置能力的关键技术,它根据感知到的环境参数,对多个目标进行参数优化,可减小发射功率、降低系统误码率和增大数据传输速率等,从而提高通信效率.目前关于认知无线电决策引擎问题的研究尚属起步阶段,文献成果较少.其中文献[3]将遗传算法应用到决策引擎中,但遗传算法存在收敛速度慢、易于早熟等问题,导致优化效率比较低;文献[4]提出了二进制粒子群算法,虽然在收敛速度上有所提高,但仍易陷入局部最优.而目前效果最好的方法是基于协进化粒子群算法(coevolutionry particle swarm optimization,CPSO)的认知决策引擎[5],与其他算法相比,在一定程度上可以提高系统的整体性能,但在易陷入局部最优和优化时间方面仍有待进一步提高.
差分进化算法是近年兴起的目前效果最好的优化算法,查阅现有文献,还没有将差分进化算法应用到认知无线电决策引擎的研究成果.为此本文进行了探索和尝试,提出一种基于二进制差分算法的认知无线电决策引擎,实验仿真结果表明,它可以在更短的时间内,获得更适合系统的工作参数,使系统整体性能有较大幅度的提高.
1 认知无线电决策引擎模型
认知无线电系统不仅需要适应动态变化的无线环境,还需要考虑到用户的应用需求、遵守特定频段的频谱特性和传播特性等参数;因此,认知决策引擎所要解决的问题可以描述成多目标优化问题,通过调整自身参数来实现多个目标最佳的性能组合[6].
假设认知无线电需要调整的参数为
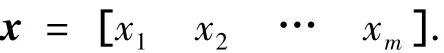
式中:m为参数的个数.
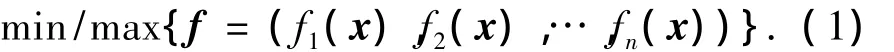
式中:f=(f1,f2,…,fn)表示所要实现的各目标函数,n为目标函数个数,则认知决策引擎所要解决的优化问题可以表示为式(1)的形式:
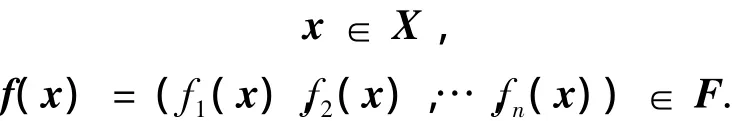
式中:X代表所要调整参数的约束空间,F代表目标函数适应度值的约束空间[7].
实际上,不同的信道条件和用户需求导致目标函数的侧重程度也不相同,例如在多媒体通信中,侧重点是最大化数据传输速率;在数据通信中,侧重点是最小化误比特率.因此,大部分文献采用式(2)的形式将复杂的多目标函数优化问题转换成单目标优化问题,通过权值的不同来满足各用户对不同目标偏好程度的需求[7].

式中:wi≥0,i=1,2,…,n,w1+w2+ … +wn=1.wi为各个目标函数的权值,权值越大代表对该目标的偏好程度越大,反之亦然.
本文与文献[8]相同,根据多载波频谱环境、用户需求以及频谱限制,选取最小化传输功率、最小化误码率以及最大化数据速率3个目标函数作为认知决策引擎的重点,进行参数优化.虽然文献[5]中将最大化吞吐量也作为一个目标函数,但是系统吞吐量主要由系统误码率决定,最小化误码率就可以保证最大化系统吞吐量,因此没有必要再引入最大化吞吐量这一目标函数.3个目标函数的归一化表达式分别为:
1)最小化传输功率:
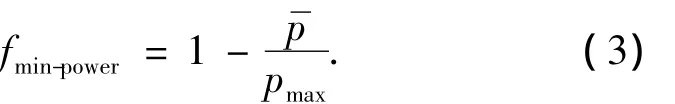
式中:pmax为子载波所能达到的最大传输功率,p为所有子载波的平均功率.
2)最小化误码率:
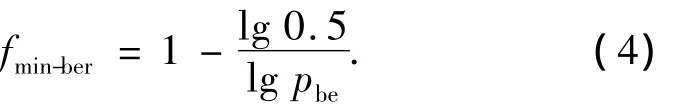
式中:pbe为所有子信道的平均误码率,定义0.5为系统所能容忍的误码率最大值,不同调制方式误码率计算公式不同,为了能够与文献[5]进行有效的性能对比,本文也选用AWGN信道条件,则M-PSK的误码率如式(5)所示.
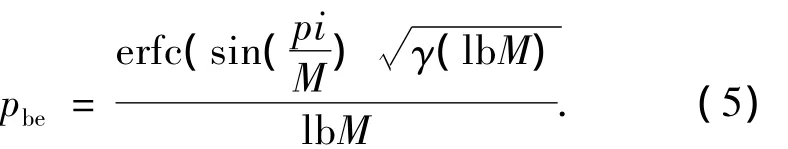
而M-QAM的误码率如式(6)所示.
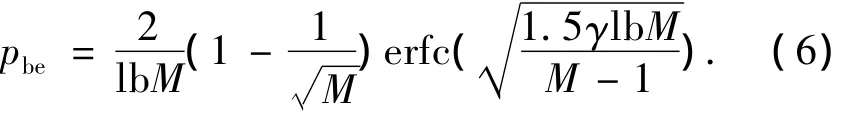
式中:M为调制进制数,γ为信噪比,erfc为互补误差函数.
3)最大化数据速率:
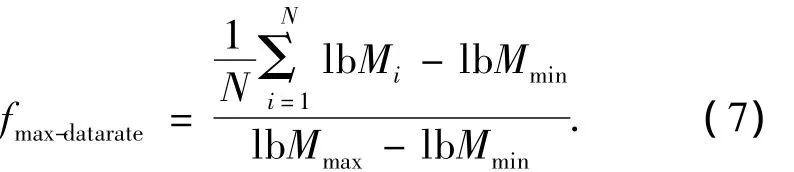
式中:N为子载波数目,Mi为第i个子载波的调制进制数,Mmin为最小调制进制数,Mmax为最大调制进制数.
由此认知决策引擎所要优化的目标函数可以表示为式(8)的形式:
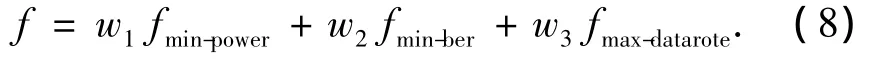
2 差分进化算法
2.1 标准差分进化算法
差分进化算法(differential evolution,DE)是1995年由Storn等提出的一种群体智能优化算法[9],2005年被引入国内.DE算法具有记忆个体最优解和种群内信息共享的特点,通过种群内个体的合作与竞争来实现对优化问题的求解,其本质是一种基于实数编码的具有保优思想的贪婪遗传算法.
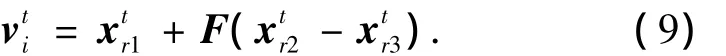
式中:r1,r2,r3∈{1,2,…,NP}互不相同且与 i不同;为父代基向量为父代差分向量;F为变异因子.然后,对个体由式(9)生成的变异个体实施交叉操作,生成试验个体如式(10)所示.
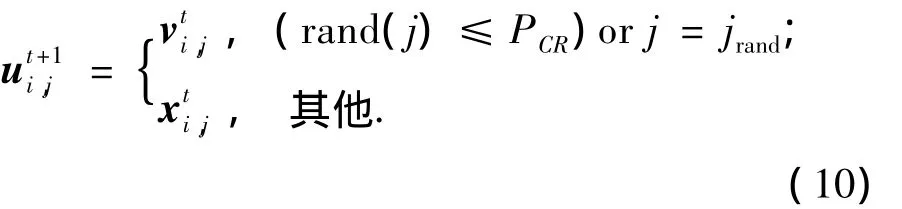
式中:rand(j)为[0,1]的均匀分布随机数;PCR为[0,1]的交叉概率;jrand为{1,2,…,D}之间的随机量.利用式(8)对试验个体的目标函数进行比较,对于最大化问题,则选择目标函数值较低的个体作为新种群的个体,如式(11)所示.
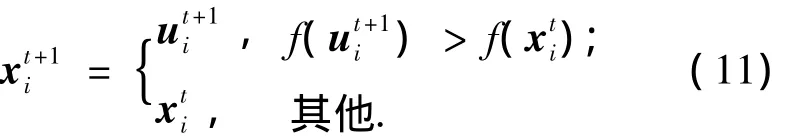
式中:f为目标函数.
DE算法流程图如图1所示.
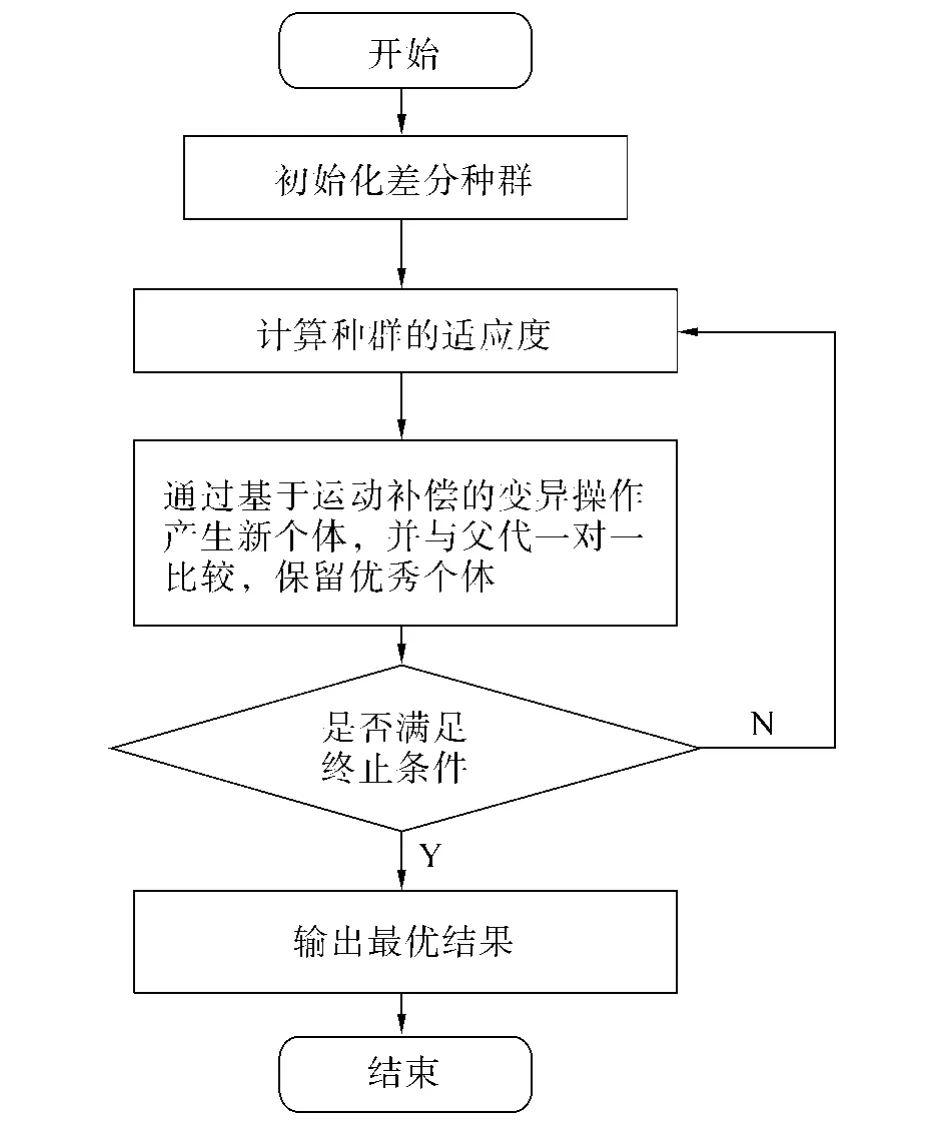
图1 差分进化算法流程Fig.1 Flowchart of DE
2.2 二进制差分进化算法
最初的DE算法主要针对解决连续空间函数优化问题,为解决离散优化问题,文献[10]提出一种二进制差分算法(binary differential evolution,BDE),可以有效解决离散函数优化问题.
与标准差分算法相比,BDE的不同之处在于问题解空间都是通过0和1编码,如果直接进行变异操作所得到的变异个体可能不符合解空间取值范围的限制,所以进行以下操作,首先按照式(12)把解向量映射到[0,1]:
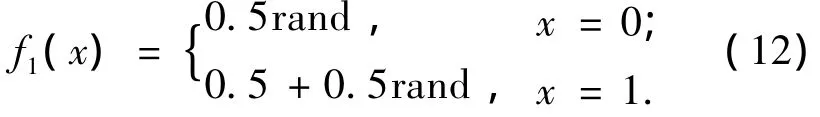
然后针对变异操作后不在[0,1]的解按照sigmoid函数映射到该范围内,如式(13)所示.
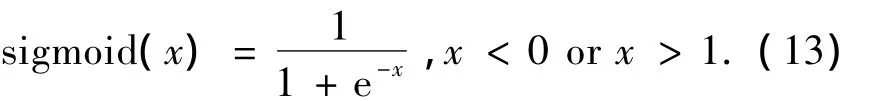
最后在交叉操作之前再将解重新解码成由0和1组成的解,如式(14)所示.
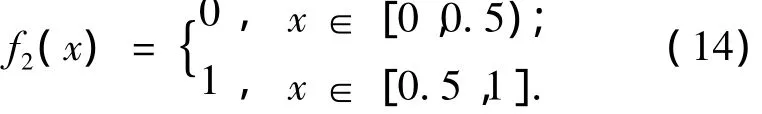
除了以上不同之外,二进制差分算法与标准差分算法类似.
3 基于BDE算法的认知决策引擎
在式(8)中,首先需要确定3个目标函数对应的权重值,为此本文采用文献[11]提供的权重值,具体如表1所示.

表1 目标函数的权重设置Tabel 1 The settings of the weight of the objective function
实际上,不同的权重值代表了系统不同的工作模式.模式1侧重于最小化传输功率,适用于低功耗情况;模式2侧重于最小化误码率,适用于可靠性要求较高的情况;模式3侧重于最大化数据速率,适用于对数据速率要求高的情况.
本文采用BDE算法对式(8)进行寻优计算,以获得认知决策引擎的最优参数组合,其具体的步骤如下:
1)设定参数:设定算法终止条件即种群最大迭代次数Max_g,初始群体规模POPSIZE,每个个体的维数为codelength,子载波数目N.
2)生成初始种群:随机生成一个POPSIZE行codelength列的矩阵,其中每行表示一个个体.
3)计算适应度:对于每个个体分别将N个子载波的功率和调制方式进行解码,根据式(3)~(7)计算 fmin-power、fmin-ber和 fmin-datarate,然后根据式(8)及表 1计算每个个体的适应度值.
4)差分和交叉算子操作:对于每个父代个体,从父代种群中随机选取2个不同的个体,并根据式(9)产生变异后新的子代;根据式(10)生成交叉后的新个体.
5)选择操作:将变异和交叉前后的个体进行适应度比较,较优的个体保留下来进入下一代.
6)重复3)~5),直到满足终止条件,其中最大适应度值对应的解就是最佳工作参数组合.
4 实验仿真与结果分析
为验证本文提出算法应用于认知决策引擎的效果,这里进行了仿真实验,并与目前效果最好的CPSO算法[5]进行对比,从而证明本文提出算法的有效性和先进性.实验是在 Inter core i7 CPU Q720,1.6GHz、内存4GB的计算机上运行,程序采用Matlab 2010b版本编写.仿真环境是基于多载波通信系统,采用32个子载波,为了模拟信道的衰落,为每个子载波分配一个区间为[0,1]的随机数.发射功率为0~25.2 dBm,步长间隔 0.4 dBm,编码由 6位二进制比特组成,调制方式可能为 BPSK、QPSK、16QAM和64QAM,由2位二进制比特进行编码,因此每个子载波功率和调制方式由8位比特进行编码.信道类型为AWGN,噪声功率为0 dBm,路径损耗为0 dB[5].在 BDE 算法中 PCR=0.6,F=0.1.在CPSO 算法中,c1=2,c2=2,vmax=4,w=1.2 种算法初始种群为30,迭代次数为1 000.
本文BDE算法与CPSO算法对3种模式分别进行30次独立的仿真实验,最后对30次仿真结果平均.图2分别给出了3种模式下平均目标函数值随迭代次数的变化情况.
图2 2种算法适应度对比Fig.2 The comparison of the fitness in twoalgorithms
从图2中可以看出,在3种模式下CPSO算法都陷入局部最优后,适应度值不再变化,同时算法结束后最优个体的适应度值都低于本文BDE算法,说明不能保证每次发现全局最优解;而本文BDE算法可以在CPSO算法陷入局部最优后,仍可以通过不断迭代提高适应度值,最终准确发现全局最优解,说明本文BDE算法的全局寻优能力强于CPSO算法.同时BDE算法在3种模式下目标函数适应度值都高于CPSO,说明在最小化功率、最小化误码率和最大化数据速率3个目标综合评价下,基于BDE的认知决策引擎在不同工作模式下整体优化性能都要优于基于CPSO的认知决策引擎.
表2给出了2种算法在不同模式下30次独立实验的平均运行时间和各目标工作性能.从表2可以看出,与目前效果最好的CPSO算法相比,本文算法在3种模式下所需要的运行时间明显少于CPSO算法所需时间,说明本文算法的认知决策引擎速度快于基于CPSO的认知决策引擎.同时在模式1下,本文算法优化后的平均功率明显小于CPSO算法优化后结果,降低了系统的功率损耗;在模式2下,本文算法优化后的平均误码率远远小于CPSO算法的结果,提高了通信质量;在模式3下,本文算法优化后的数据速率大于CPSO算法的结果,提高了系统的通信效率.
表2 2种算法优化时间及结果对比Tabel 2 The time and results of two algorithms
综上所述,本文提出的基于BDE算法的认知决策引擎整体优化性能优于基于CPSO的认知决策引擎,并且工作效率和对偏好目标工作性能都明显优于CPSO算法.
5 结束语
针对认知无线电决策引擎调整工作参数问题,本文提出了一种基于BDE算法的认知决策引擎算法.实验仿真结果表明,本文提出的算法能够快速得到最佳工作参数,同时使整体优化性能更好,并且在不同模式下针对主要优化目标取得更好的工作性能,更适合解决认知决策引擎实际问题,在认知无线电系统中具有一定的实用价值.
[1]NEWMAN T R,RAJBANSHI R,WYGLINSKI A M,et al.Population adaptation for genetic algorithm cognitive radios[C]//Proceedings of the 2nd International Conference on Cognitive Radio Oriented Wireless Networks and Communications.Orland,USA,2007:279-284.
[2]郭彩丽,冯春燕,曾志民.认知无线电网络技术及应用[M].北京:电子工业出版社,2010:14-15.
[3]ZHANG X Q,HUANG Y Q,JIANG H,et al.Design of cognitive radio node engine based on genetic algorithm[C]//2009 WASE International Conference on Information Engineering.Taiyuan,China,2009:22-25.
[4]POVALAC K,MARSALEK R.Adjusting of the multicarrier communication system using binary particle swarm optimization[C]//Proceedings of 19th International Conference Radioelektronika 2009.Bratisalava,Slovakia,2009:251-254.
[5]赵知劲,张伟卫,彭振,等.基于协进化粒子群优化的认知决策引擎[J].计算机工程,2011,37(3):163-165.ZHAO Zhijin,ZHANG Weiwei,PENG Zhen,et al.Cognitive decision engine based coevolutionry particle swarm optimization[J].Computer Engineering,2011,37(3):163-165.
[6]赵知劲,徐世宇,郑仕链,等.基于二进制粒子群算法的认知无线电决策引擎[J].物理学报,2009,58(7):5118-5125.ZHAO Zhijin,XU Shiyu,ZHENG Shilian,et al.Cognitive radio decision engine based on binary particle swarm optimization[J].Acta Physica Sincia,2009,58(7):5118-5125.
[7]焦传海,王可人.一种基于免疫遗传算法的认知决策引擎[J].系统工程与电子技术,2010,32(5):1083-1087.JIAO Chuanhai,WANG Keren.Cognitive radio decision based on immune genetic algorithm[J].Systems Engineering and Electronics,2010,32(5):1083-1087.
[8]WU D,WANG F,YANG S Y.Cognitive radio decision engine based on priori knowledge[C]//Proceedings of 3rd International Symposium on Parallel architectures,Algorithms and Programming.Dalian,China,2009:346-349.
[9]毕晓君,王义新.多模态函数优化的拥挤差分进化算法[J].哈尔滨工程大学学报,2011,32(2):223-227.BI Xiaojun,WANG Yixin.Multimodal function optimization using a crowding differential evolution[J].Journal of Harbin Engineering University,2011,32(2):223-227.
[10]DENG C S,ZHAO B Y,YANG Y L,et al.Novel binary differential evolution algorithm for discrete optimization[C]//5th International Conference on Natural Computation.Tianjin,China,2009:346-349.
[11]NEWMAN T R.Cognitive engine implementation for wireless multicarrier transceivers[J].Wireless Communications and Mobile Computing,2007,7(1):1129-1142.

