无线传感器网络环境下基于卡尔曼滤波的PTP协议

叶玲，李太华，代学武

(西南大学电子信息工程学院，重庆400715)

保持节点之间时间上的同步在分布式系统中具有十分关键的地位，是保证各节点协同工作，处理数据正确和信息传输可靠的前提.时间同步(time synchronization)是一个将各分布式节点上的时钟对准的过程，其目的是把各节点和设备的时钟偏差限定在足够小的范围内.作为分布式系统的一个重要分支，无线传感器网络的很多应用依赖于时间同步［1］，比如数据融合、TDMA 调度、基于 TOF(time of flight)定位技术［2］、面向波束成形(beam forming)的多节点协同技术［3］等.无线传感器网络具有能量受限、计算能力低、通信容量低等特点［4］.无线网络节点的时钟通常是通过本地的晶振和中断机制来实现的，受制造误差、温度变化、CPU处理延迟等影响较明显.因此，实施高精度的时间同步算法是一项具有挑战性的工作.

目前在数据包交换网络中，广泛使用的时间同步算法主要采用时间信息包交换技术，其研究的内容主要是如何通过时间信息的交换来提高不够精确的时钟的精确度，比如因特网上广泛采用的NTP协议、针对工业以太网的IEEE 1588 PTP等.针对无线传感器网络已陆续出现多种时间同步协议，主要可以分为以下几类:1)基于发送者—接收者的双向同步，典型算法如 TPSN［5］(timing-sync protocol for sensor networks)算法;2)基于发送者—接收者的单向时间同步，如 FTSP［6］(flooding time synchronization protocol)算法和 DMTS［7］(delay measurement time synchronization)算法;3)基于接收者—接收者的同步算法，如 RBS(reference broadcast synchronization)［8］算法.但它们未能在能效和精度上进行充分的优化［9］.针对有线包交换网络，已经形成了一个IEEE 1588精确时间同步协议(precision time synchronization protocol，PTP)标准［10］.在一定条件下，其时间同步的精度可以控制在微秒范围内，该同步的精度远高于基于 NTP时间同步协议.相比于FTSP等时间同步协议，由于PTP操作简单、对带宽的要求相对较低，更适合于通信带宽和能量受限的无线传感器网络设备.上述特点使其在同步精度和功耗上能够实现较好的平衡.但由于IEEE1588 PTP协议是针对有线网络提出的，如何将PTP运用于无线传感器网络以提高无线网络的时间同步精度尚未有定论，国际和国内相关的工作才刚刚展开.因此本文重点研究如何利用卡尔曼滤波器在无线传感器网络中实现高精度的时间同步.

时间同步的本质是一个用通信带宽和计算功耗换时间精度的问题，受到通信延迟抖动(与通信带宽相关)和时间戳精度(与CPU处理能力相关)的影响很大.基于时间信息包交换的时间同步过程涉及2个方面:有偏差的物理时钟和时间信息交换协议(即时间同步算法).为了更好地研究时间同步，需要对物理时钟和时间信息交换分别进行建模.时钟模型主要有2种比较典型的方案:1)采用基于时钟振荡器物理特征的差分方程进行描述［11］.在真实的无线传感器网络中，节点时钟频率漂移在不同时期服从不同规律.因此该方案的关键是获取差分方程模型的参数.2)采用一阶高斯马尔可夫链模型，也称一阶自回归模型(autoregressive，AR)来描述时变的时钟漂移［12］.

本文尝试将PTP协议用于无线传感器网络，主要研究PTP时间同步精度与时钟戳的不确定性和延迟抖动之间的数量关系.利用AR时钟模型构建时钟的状态转移方程，将PTP协议建模为一组观测方程，然后基于卡尔曼滤波器对时钟偏移(offset)和时钟偏移率(skew)进行跟踪，以提高PTP同步协议在无线传感器网络的时间同步的性能.

1 系统建模

1.1 时钟模型

时钟建模使用状态转移方程组来描述网络节点自身的本地(物理)时钟变化规律，而物理时钟通常有偏差且不精确.如图1所示，横坐标表示基准时间(或全局时间)t，纵坐标表示一个节点有误差的本地时间C(t).C(t)具有分段线性特征，除在可数点集P⊂R(集合P表示时钟参数发生改变的情况)外二次可导的函数，即dC2(t)/dt2在t∉P时总是存在的.C(t)可表示为

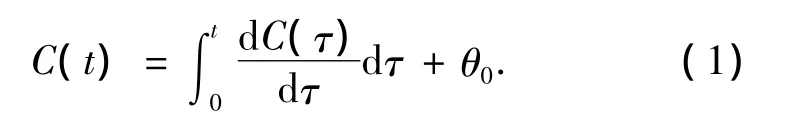
式中:θ0为时钟偏移的初始值，dC(t)/dt为时钟变化率，也称作时钟变化频率偏移，描述了本地时钟的频率.理想情况下，精确时钟C(t)=t，其时钟变化率为dC(t)/dt=1且P=∅.

图1 时钟漂移模型Fig.1 Clock model

在此后的论述中，用TM(t)=t来表示精确时钟，即主时钟或全局时钟.时钟偏移θ用来描述本地时钟C(t)和全局时钟 TM(t)之间的差值，θ=TM(t)－C(t).时钟偏移率 α=1－dC(t)/dt，描述了本地时钟频率和全局时钟频率之间的差异.

本地软件时钟模型主要描述软件时钟和物理时钟的关系，常用模型是:软件时钟对硬件时钟值作仿射变换，硬件时钟是只读的，即不能更改硬件时钟速率.不同的软硬件配置有不同的软件时钟模型.本文中软件时钟的值是把物理时钟的值根据θ和α来修正后得到的.

由于时钟偏移率α通常会受温度等环境因素影响，但比较缓慢，通常可以假设在一个较小的时间间隔内，α是不变的.因此，通过离散化处理，连续时钟模型(1)可转化为一组离散时间域上的状态转移方程:

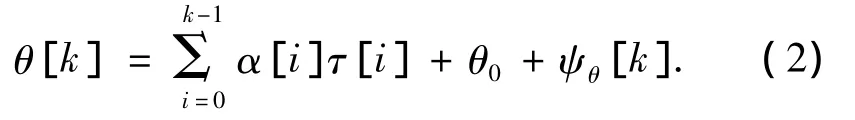
式中:θ0是初始时钟漂移(即t=0时刻的时钟漂移值)，α［i］是时间段 τ［i］内的时钟偏移率(0≤i≤k－1)，ψθ［k］是瞬时的时钟偏移波动 ωθ［k］的累积和，即 ψθ［k+1］= ψθ［k］+ ωθ［k］.将式(2)写成递归的形式，则时钟偏移的状态转移方程为

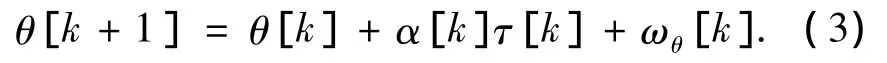
根据文献［12］，时钟偏移率的变化可以用一个AR过程来描述，于是α的状态转移方程为

式中:τ［k］为时间同步间隔(即2次同步之间的时间间隔)，本文中假定为固定不变，即τ［k］=ΔT;ωθ［k］代表时钟偏移的白噪声;ωα［k］代表时钟偏移率的噪声(白频率噪声).ωθ［k］和 ωα［k］是 2 个不相关的高斯白噪声过程，方差分别为和.

1.2 PTP时间同步协议模型

PTP协议［10］是一种主从时钟同步协议，其基本原理是:从节点通过与主节点交换包含时间标记的时间信息包，计算出主从节点之间的时钟偏移θ，从而估计出主节点的时间，并调整从节点的本地时钟使其与主时钟保持同步.PTP中的时间标记信息包交换过程如图2所示.

图2中t1和t2为一次同步中主从时钟记录下的时间标记，t3和t4为紧接着的一次Delay_Req请求报文传输过程中，从时钟和主时钟记录下的时间标记.考虑到主从之间数据包的传输延迟，它们之间的关系如下:

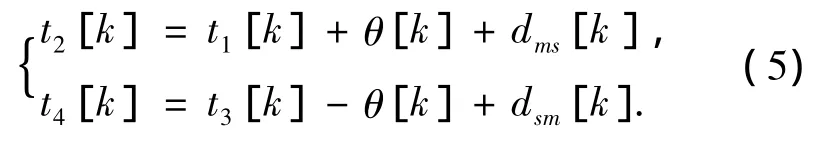
式中:k代表第k次时间同步过程，dms代表数据包从主时钟到从时钟的传播时延，dsm代表数据包从从时钟到主时钟的传播时延.将主从时钟间的时钟偏移θ看作待求解未知量，解方程组(5)，可得到

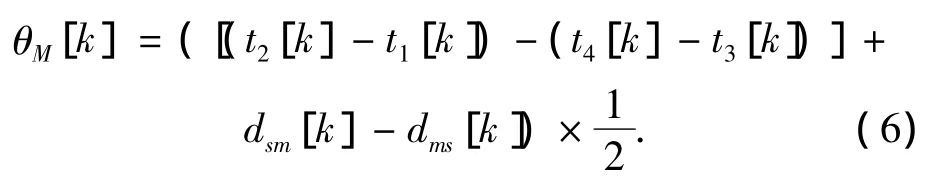
式(5)描述了时间同步协议中时间标记信息包交换过程中主从时间标记之间的关系.式(6)是时钟偏移的观测方程，描述了如何从时间信息包交换中“测量”出主从时钟偏移.

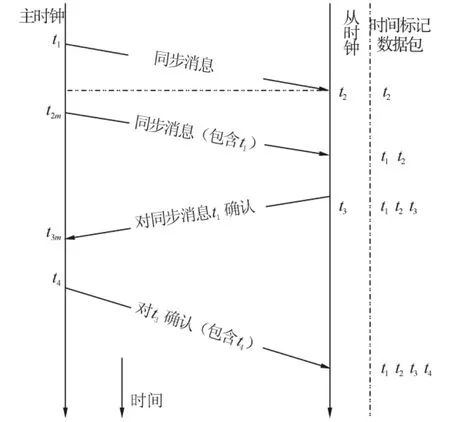
图2 PTP协议时间标记包交换过程Fig.2 Timing diagram of message exchange by PTP

在PTP时间同步协议中，传输时延假定对等，即dsm=dms.但实际网络中由于无线介质的共享、冲突退避和重发等因素，数据包的传输时延不会相等，即dsm≠dms.在这里，将传输延迟的不对等性可以用延迟抖动来描述，即把传输时延dsm和dms看作一个均值为d、方差为的高斯随机过程N(d，σd)的2次取值.令 Δd=(dsm－dms)/2，计算 θ的式(6)可写为

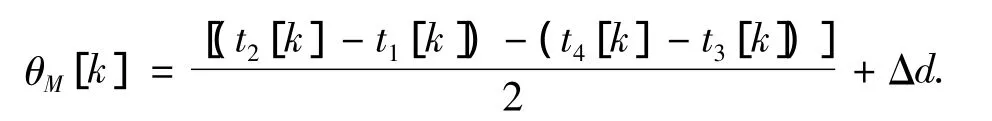
式中:Δd描述了传输延迟的不对称性，Δd是一个均值为0，方差为1/2×的高斯随机变量.进一步考虑由于嵌入式系统中断处理延迟等所造成时间戳的不确定性，在主从时钟的观测值ti中，同样存在时钟值读取误差 Δti(i=1，2，3，4)，Δt1和 Δt4是主时钟的盖戳的不确定性，Δt2和Δt3是从时钟的盖戳的不确定性.于是θ的观测方程为

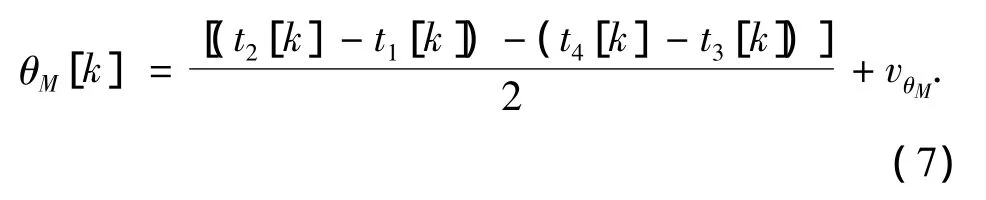
式中:vθM代表θ的观测噪音，定义为

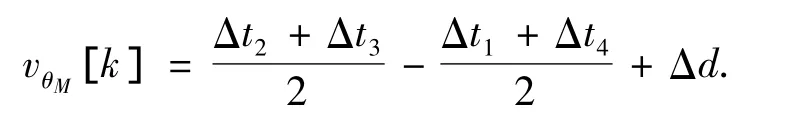
观测噪音 vθM是时间标记误差 Δti(i=1，2，3，4)与传输延迟不对称性Δd之和.假设时间标记的不确定性是零均值的独立随机变量是 Δt1和Δt4的方差是 Δt2和 Δt3的方差，则 vθM的方差是各个独立随机变量的方差之和:

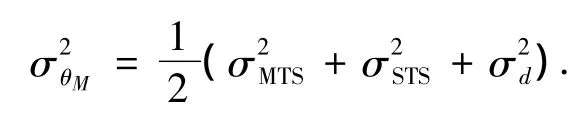
因为Δt2和Δt3的均值不为零(时间延迟始终是个正数)，故vθM的均值不为0，而是Δt2和Δt3的平均值相加.假定在一个同步周期τ［k］内恒定不变，则时钟偏移率α［k］可以从θ的观测值中计算出来，α［k］的观测方程为

同理，可以得到αM［k］的观测噪音的方差为

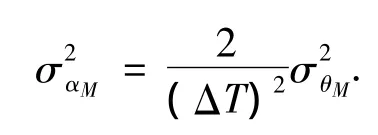
注意，由于αM［k］是从θ的观测值得到的，观测噪音 vαM与 vθM相耦合，它们的协方差为

2 基于卡尔曼滤波器的时间同步

假设基于主从时钟包交换所获取的时间信息是绝对精确且可靠的，则如第1部分所述的关于时钟偏移和时钟偏移率的观测值可直接用于矫正本地时钟，以实现时间同步.然而，由于主从时钟包交换过程中存在着各种不确定因素，期间获取的时间信息通常是不精确且不可靠的.因此，需要通过滤波器技术对其进行预处理.在第1部分已经建立的递归时钟模型和同步协议模型的基础上，可以利用卡尔曼滤波器方程实现递归估计器.

基于这一目的，正如第1部分所述，从式(7)和式(8)可以得到观测方程:

将状态转移方程(3)、(4)和观测方程(9)写成矩阵形式，可建立时钟同步的状态空间模型:

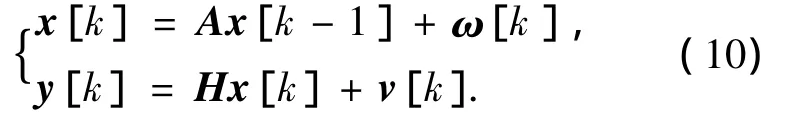
式(10)分别称为时钟状态方程和观测方程.式中:x［k］=［θ［k］ α［k］］T为第 k 轮时钟状态向量;y［k］=［θM［k］ αM［k］］T为第 k 轮时钟观测向量;，为状态转移矩阵为测量系统的参数矩阵，它将真实状态空间映射到观测空间;=［vθM［k］ vαM［k］］T分别表示过程噪声和观测噪声，ω［k］服从 N(0，Q)正态分布，v［k］服从N(0，R)正态分布，且两噪声的各样本间均相互独立.v［k］的零均值假设在实际系统中并不一定成立，v［k］的均值同样是一个与发送节点、接收节点相关的变量，尽管如此，在v［k］均值未知的情况下对其进行零均值的假设是开展卡尔曼滤波所要求的条件，而零均值的假设所引入的误差最终将体现在时钟同步误差的均值上.在这里，设定

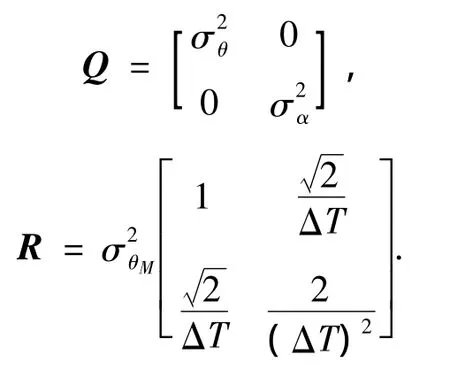
由此，卡尔曼滤波器的迭代算法过程可以描述成如式(11)、(12):

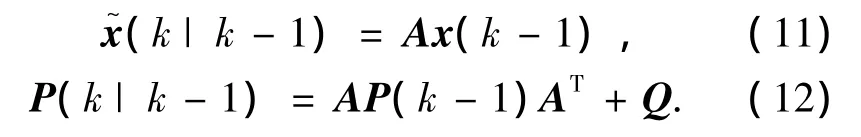
式(13)～(15)为更新过程:

3 实验结果分析

在这一部分，基于不同观测噪声条件，主要分析主从时钟之间，时钟偏移和时钟偏移率估计误差平均值和标准差的变化趋势.

在仿真实验中，时钟模型(式(3)、(4))用来仿真不精确时钟，最小步长是10－6s，远远小于时钟同步周期ΔT(在仿真实验中ΔT=0.1 s)，ΔT同样是卡尔曼滤波器进行迭代算法的周期.

对于时间同步的精确度的衡量，采用了时钟偏移的估计误差和时钟扭曲率估计误差这2项指标，分别用估计误差的均值和估计误差的方差来表示.

图3、4反应了在不同σSTS取值下，主从时钟在时钟偏移(offset)和时钟偏移率(skew)估计误差均值的变化趋势，体现了时钟可靠性的变化规律.

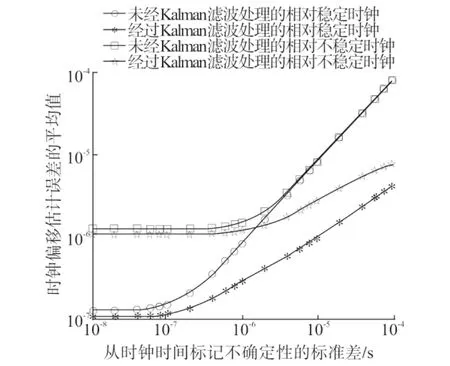
图3 时钟偏移估计误差的平均值Fig.3 Offset estimation error mean

图4 时钟偏移率估计误差的平均值Fig.4 Skew estimation error mean

由图3可知，随着时间标记不确定性的增加，时钟偏移估计误差均值在2种算法模式下均呈现增加趋势，但基于卡尔曼滤波器的PTP算法的均值明显小于无卡尔曼滤波器的PTP算法.针对不同的时钟类型，可以看出相对稳定时钟，在不同算法模式下其估计误差均值均低于相对不稳定时钟.但同样可以看出同一时钟在2种算法模式下，当时间标记不确定性很小时，时钟偏移估计误差均值差别不显著，但随着时间标记不确定性增大，基于卡尔曼滤波器伺服的PTP算法的优势则十分显著.

由图4知，随着时间标记不确定性的增加，时钟偏移率估计误差均值在无卡尔曼滤波器的算法模式下呈现显著增大趋势，但在基于卡尔曼滤波器的PTP算法模式下，估计误差均值则表现出相对的稳定性，且明显小于无卡尔曼滤波器的PTP算法.针对不同的时钟类型，可以看出相对稳定时钟，在不同算法模式下其估计误差均值均低于相对不稳定时钟.

由图5可知，随着时间标记不确定性的增加，时钟偏移估计误差的标准差在2种算法模式下均呈现增加趋势，但基于卡尔曼滤波器的PTP算法的标准差明显小于无卡尔曼滤波器伺服的PTP算法.针对不同的时钟类型，可以看出，相对稳定时钟，在不同算法模式下其估计误差的标准差均低于相对不稳定时钟.但同样可以看出，同一时钟在2种算法模式下，当时间标记不确定性很小时，时钟偏移(offset)估计误差的标准差差别不显著，但随着时间标记不确定性增大，基于卡尔曼滤波器的PTP算法的优势显著.

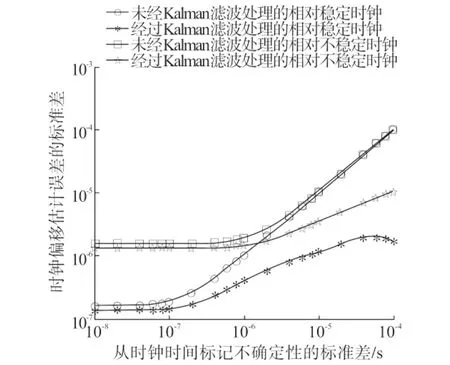
图5 时钟偏移估计误差的标准差Fig.5 Offset estimation error standard deviation

由图6可知，随着时间标记不确定性的增加，时钟偏移率估计误差的标准差在无卡尔曼滤波器的模式下呈现显著增大趋势，但在基于卡尔曼滤波器的PTP模式下，估计误差的标准差则表现出相对的稳定性，且明显小于无卡尔曼滤波器伺服的PTP算法.针对不同的时钟类型，可以看出相对稳定时钟，在不同算法模式下其估计误差的标准差均低于相对不稳定时钟.值得注意的是，图6中时钟偏移率估计误差的标准差在前一段存在一变小趋势，这需要更加精确的理论推导证明.

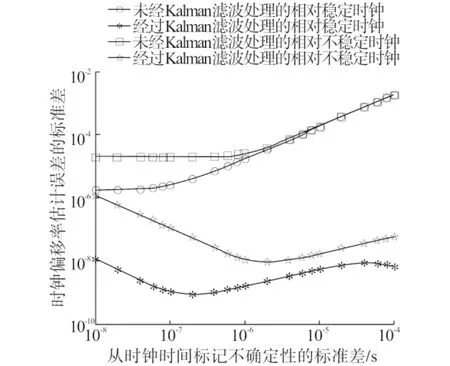
图6 时钟偏移率估计误差的标准差Fig.6 Skew estimation error standard deviation

主从时钟时钟偏移和时钟偏移率估计误差均值和标准差反映了时钟同步算法的精度和稳定性.综合图3～6可知，基于卡尔曼滤波器的PTP时钟同步算法对主从时钟在时钟偏移和时钟偏移率的估计，无论是精度还是稳定性，均优于无卡尔曼滤波器的PTP时钟同步算法.但是，当观测噪声比较小，即从时钟时间标记不确定性非常小时(比如，σSTS=10－8s)，基于卡尔曼滤波器的PTP时钟同步算法优势不显著，而随着观测噪声逐步增大时，基于卡尔曼滤波器的PTP时钟同步算法优势则愈发显著.因此，基于卡尔曼滤波器的PTP时钟同步算法比较适用于观测噪声较大的应用中.标准的无线传感器网络节点时钟之间标记不确定性的标准差σSTS在10－5左右［15］.由图3～6可以看出，当观测噪声处于这一量级时，基于卡尔曼滤波器的PTP时钟同步算法优势已十分显著.因此，基于卡尔曼滤波器的PTP时钟同步算法适用于无线传感器网络的应用.

根据仿真实验结果(图3～6)可知，稳定性不同的2类时钟，在2种不同时钟同步算法模式下，当观测噪声较小时，比如σSTS≤10－5时，相对稳定的时钟的时钟同步精度和稳定性均优于相对不稳定的时钟.但是当观测噪声较大时，比如σSTS＞10－5时，则相对稳定的时钟的时钟同步精度和稳定性相对不稳定的时钟虽有优势，但趋于不显著，特别是在无卡尔曼滤波器的PTP时钟同步算法模式下.因此，可以得出结论，当观测噪声较大时，选择具有高稳定度(往往价格更高)时钟的无线传感器网络节点已无必要.

4 结束语

本文对基于卡尔曼滤波器的PTP时间同步算法进行了理论分析、建模和仿真，并与无卡尔曼滤波的PTP时间同步算法就时钟估计误差精度和稳定性进行比较研究.实验结果显示，基于卡尔曼滤波器的时间同步算法在精度和稳定性上有明显的优势，并为在真实物理环境中配置无线传感器网络提供了参考，比如在不同噪声环境下，节点时钟精度的选择等.

［1］SUNDARARAMAN B，BUY U，KSHEMKALYANI A D.Clock synchronization for wireless sensor networks:a survey［J］.Ad Hoc Networks，2005，3(3):281-323.

［2］CAPKUN S，CAGALJ M，SRIVASTAVA M.Secure localization with hidden and mobile base stations［C］//Proceedings of 25th IEEE International Conference on Computer Communications.Barcelona，Spain，2006:1-10.

［3］MUDUMBAI R，BARRIAC G，MADHOW U.On the feasibility of distributed beamforming in wireless networks［J］.IEEE Transactions on Wireless Communications，2007，6(5):1754-1763.

［4］LIU Q，LIU X，ZHOU J，et al.Adasynch:a general adaptive clock synchronization scheme based on Kalman filter for WSNs［J］.Wireless Personal Communications，2012，63(1):217-239.

［5］GANERIWAL S，KUMAR R，SRIVASTAVA M B.Timingsync protocol for sensor networks［C］//The First ACM Conference on Embedded Networked Sensor System.New York，USA，2003:138-149.

［6］MAROTI M.The flooding time synchronization protocol［C］//Proc 2nd ACM Conf Embedded Networked Sensor Systems.New York，USA，2004:39-49.

［7］PING S.Delay measurement time synchronization for wireless sensor networks IRB-TR-03-013［R］.Berkeley:Intel Research，2003.

［8］ELSON J，GIROD L，ESTRIN D.Fine-gained network time synchronization using reference broadcasts［C］//Proc fifth Symposium on Operating Systems Design and Implementation.New York，USA，2002:147-163.

［9］ZENG Y，HU B，LIU S.Vector Kalman filter using multiple parents for time synchronization in multi-hop sensor networks［C］//Proc of the IEEE SECON.San Francisco，USA，2008:413-421.

［10］EIDSON J C，FISCHER M，WHITE J.IEEE 1588 standard for a precision clock synchronization protocol for networked measurement and control systems［S］//IEC 61588(E):2004-IEEE Std.1588(E)，2002.

［11］GALLEANI L，SACERDOTE L，TAVELLA P，et al.A mathematical model for the atomic clock error［J］.Metrologia，2003，40(3):257-264.

［12］HAMITON B R，MA X，ZHAO Q，et al.Aces:adaptive clock estimation and synchronization using Kalman filtering［C］//Proceedings of the 14th ACM International Conference on Mobile Computing and Networking.New York，USA，2008:152-162.

［13］ABUBAKARI H，SASTRA S.IEEE 1588 style synchronization over wireless link［C］//Proc IEEE ISPCS.Ann Arbor，USA，2008:127-130.

［14］BARENDT N，CORRELL K，BRANICKY M.Servo design considerations for software-only implementations of the precision time protocol［C］//ISPCS.Zurich，Switzerland，2005:10-12.

［15］SAVVIDES A，HAN C，SRIVASTAVA M.Dynamic finegrained localization in ad-hoc networks of sensors［C］//Proceedings of the 7th Annual International Conference on Mobile Computing and Networking.New York，USA，2001:166-179.