田径运动技术评定的模糊集重心改进算法

吴志远，王远干

(钦州学院数学与计算机学院,中国 钦州 535000)

在田径运动教学中，评定学生田径运动技术是田径教学考核的一个重要方面，也是科学管理与控制教学过程的一个不可缺少的重要环节[1]．利用评定得到的反馈信息可以及时查找教学中存在的问题，不断改进教学方法，优化教学过程，提高教学质量[2]．因此，田径运动技术评定方法、评定标准科学与否，不但影响到评价结构的客观性和公正性，还会影响到反馈信息的有效性和可靠性，影响到田径教学的教学改革．

目前评定运动技术所采用的方法，主要有专家评分法、模糊综合评价法等．由于种种原因，专家评价法的评价标准难以把握和统一，导致评价结果受到个人主观影响较大，不能准确反映真实情况[3]．模糊综合评价法能较好地处理运动技术评价问题中的模糊信息，很受学者们青睐[4-5]，但它也存在不足，比如模糊综合评价法采用模糊合成算子，在复合过程中强调极值的作用，造成信息丢失较多[6-8]．为此，作者引入模糊集重心算法．传统的模糊集重心算法利用模糊关系重心替换模糊关系合成，从一定程度上克服了模糊综合评价法信息丢失问题，但还存在不足．一是传统的模糊集重心算法只允许专家直接给出一个具体的隶属度，因此专家很难准确地给出评语[9]；二是传统的模糊集重心算法往往采用模糊统计法建立模糊关系矩阵[10]，该方法虽然操作方便简单，但不能充分利用专家意见，也会产生信息丢失．为此，作者对基于模糊集重心算法的田径技术评价模型进行了改进，改进模型允许专家通过模糊区间分来评测指标，然后再分别计算区间分端点的重心，最后考虑各因素的权重和专家的权威给出决策意见．改进的评价模型克服了专家评分法的主观性和模糊综合评价等方法的信息丢失问题，并且结构简单，不但便于专家操作，还可以充分利用专家的评测意见，是解决体育运动技术测评的无结构决策性问题的有效方法．

1 模糊集重心的定义

设U为实数域R中的有界可测集，则U上的模糊集A的隶属函数μA(x)的重心定义为

(1)

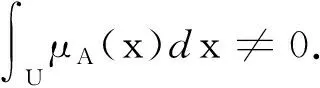
特别地，当论域U={x1,x2,…,xn}⊂R(R为实数域)时，上述(1)式可表示为[11-12]

(2)

模糊集的重心描述了模糊集的隶属度在论域U内集中的位置．当隶属函数一定时，其重心的位置也是一定的[13]．由此可见，模糊集重心是模糊集的一个固有属性，它刻画了模糊集的隶属函数在论域U内集中的位置，因而可以用模糊集重心来描述隶属函数的分布情况．

2 基于改进模糊集重心算法的田径运动技术评定方法

基于改进模糊集重心算法的田径技术评定模型，利用田径技术评价指标的隶属函数的重心进行综合评价，根据田径技术评价指标实际情况，通过计算专家的模糊区间分的重心，确定重心位置，然后再根据评价指标的权重和专家的权威确定评价结果．基本步骤为:

(1) 建立评价体系．某种田径运动技术的高低往往要从多个因素(或技术指标)去综合评价，不妨设有n个因素，因而因素集为U={U1,U2,…,Un}．根据U中各因素Ui(1≤i≤n)对U的重要程度的不同，给每个因素相应地赋予一个权重，各因素的权重为W=(w1,w2,…,wn)；

图1 语言值标尺

(2) 确定评语集．采用常用的由5个等级所组成的评语集：V={v1,v2,v3,v4,v5}={差，合格，一般，良好，优秀}．为了方便专家的给分，将这5个评语置于一个连续的语言值标尺上，且每个评语在标尺上的长度设为1，见图1．

图2 打分格式

(3) 专家评分．为了方便专家表达评测意见，提高评判的客观性和可靠性，允许专家通过用一个模糊区间分来评测一个技术指标，打分格式如图2所示，其中用uimin j、uimax j分别表示专家给出的指标的最小值模糊区间分和最大值模糊区间分，i表示第i个因素，j对应于第j个评语．

(3)

(4)

综合m个专家的意见，可得ui的最大重心Gimax和最小重心Gimin分别为

(5)

(6)

从而得U的最大重心Gmax和最小重心Gmin分别为

(7)

(8)

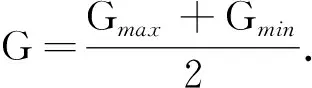
3 基于改进的模糊集重心算法的田径运动技术评定实例

为了说明以上算法的可行性和实用性，现就田径中的背越式跳高技术评定为例，评定某位学生的背越式跳高技术水平．

通过查阅资料[14-15]和咨询专家，认为背越式跳高技术与助跑、起跳、过杆、落地4个方面有密切关系，所以评价因素集为U={助跑U1，起跳U2，过杆U3，落地U4}．设评价因素的权重系数为W=(0.15,0.54,0.25,0.06)，评价集为V={差，合格，一般，良好，优秀}．

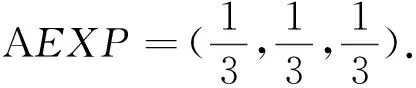
对于其他专家，其他指标的计算与此类似，为了节约篇幅，不再赘述．

表1 专家1对各技术指标的评分及其重心值

当我们得到3位专家评价的最大重心值、最小重心值后，由公式(5)、(6)可以计算出各技术指标的综合模糊集重心值，见表2．其中，技术指标1：助跑的最大重心和最小重心分别为

表2 3位专家对方案评价所得重心值

下面计算该学生背越式跳高技术得分的最大重心和最小重心，由公式(7)、(8)得

4 实验仿真结果对比与分析

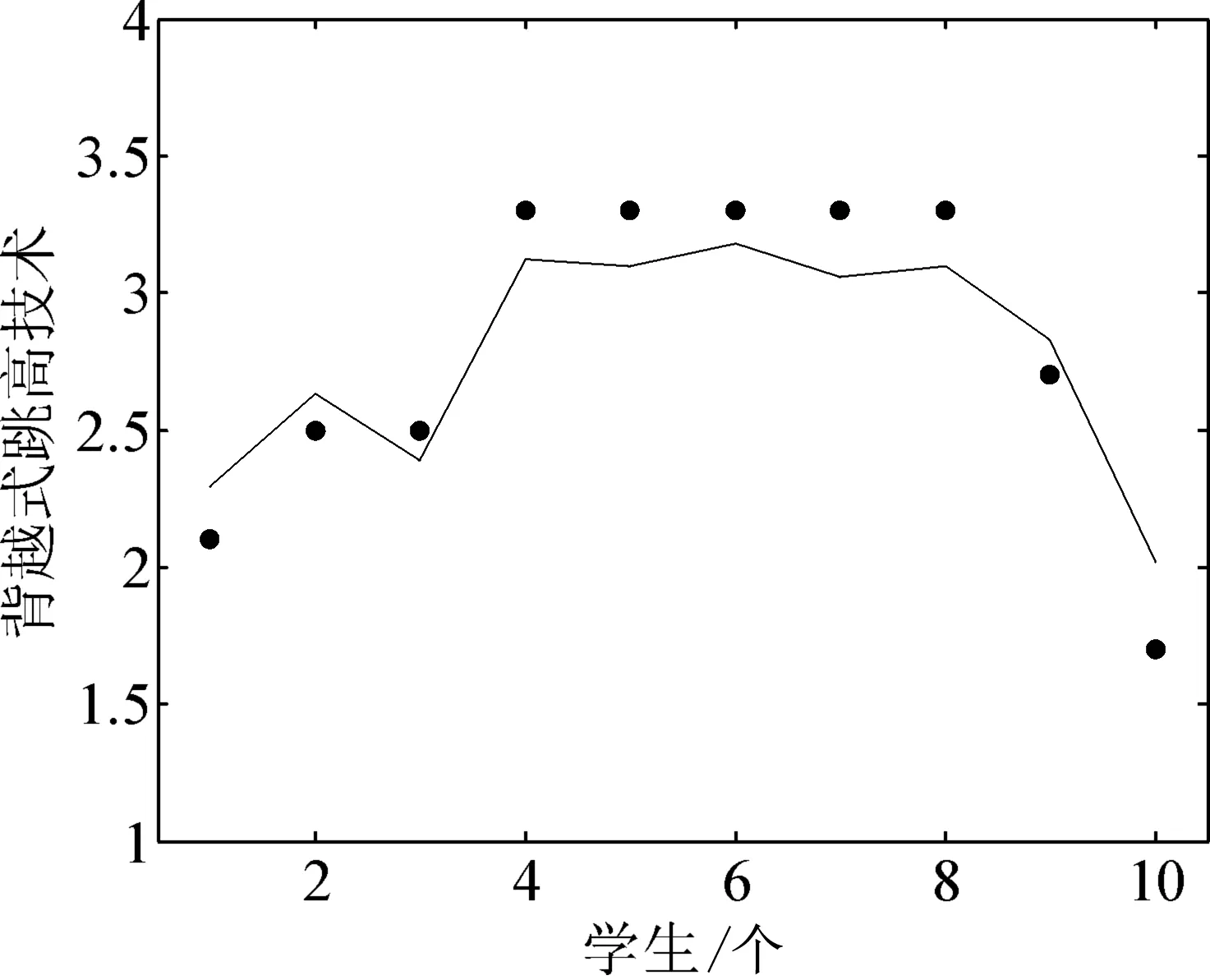
图3 两种方法仿真结果对比

为了对比本文方法的优势，采用传统模糊集重心评价法和改进模糊集重心评价法进行了仿真实验．项目组成员在本校体育学院组织了5名体育教师对体教本091班的10名学生采用2种评价方法进行了仿真测试，图3是2种方法得到的结果，其中，点状图为传统模糊集重心评价法得到的结果，线状图为改进模糊集重心评价法得到的结果，两者之间的距离反应出算法偏差．从图中可以看出，2种算法的结果有一定的偏差，其中，第十位学生，利用改进模糊集重心评价法得到的技术等级为“一般”，利用传统模糊集重心评价法得到的技术等级为“合格”，相差甚大．

通过分析，出现偏差的主要原因是传统模糊集重心评价法在采用模糊统计法建立模糊关系矩阵时产生了信息丢失，专家在(t-1,t]区间里随意给一个分值，这个分值对评价结果贡献都是一样的，因此不能充分利用每位专家的评价意见，评价结果出现了一定偏差．在改进模糊集重心评价法中，评价指标的重心和评价对象的评语都是由各个评价指标在各个评语上的评测信息综合产生的，充分利用了专家的评价意见，因此，可以克服传统方法的弊端，判断准确性大幅提高．

5 结束语

评定学生田径运动技术是科学管理与控制教学过程的一个不可缺少的重要环节，传统的评价方法由于其存在一定的局限性，不能准确反映教学效果，也不能从评价结果得到有价值的反馈信息，在一定程度上影响了学生学习的积极性和教学改革．本文提出了一种基于模糊集重心算法的评价模型．该算法不但给出了一个与人们思维模式一致的连续语言值标尺，还允许专家利用一个模糊区间分来评测指标，因而非常有利于专家表达其思想．在改进的模糊集重心评价法中，评价指标的重心和评价对象的评语都是由各个评价指标在各个评语上的评测信息综合产生的，充分利用了每一位专家的每一个数据，因此评价结果科学、合理．测评实例的数值仿真结果也验证了模糊集重心改进算法的实用性与有效性．

参考文献：

[1] 刘永东.田径运动技术客观化评定方法的探讨[J].湖北体育科技, 2001,20(1):82-84.

[2] 陈燕萍.运用系统论和控制论评价田径运动教学效果[J].福建体育科技, 1999,18(2):63-64.

[3] 吴向明.论田径技术评定中存在的几个问题[J].成都体育学院学报, 2002,28(5):78-80.

[4] 汪 鸿.运用模糊数学方法对田径运动技术进行综合评定的研究[J].体育科研, 2004,25(1):47-49.

[5] 唐 艺，梁 刚.基于优化组合的高校体育理论题库的研究与设计[J].湖南师范大学自然科学学报， 2011，34(5)：41-45.

[6] 郑双忠,刘艳军,丁明祯,等.基于模糊重心的建筑火灾危险性评价[J].东北大学学报, 2004,25(3):283-286.

[7] 范玉茹,隋立芬,马 莉.基于模糊集重心的DLG产品质量的模糊综合评判[J].测绘科学, 2011,36(5):155-156.

[8] 阚新玉.基于模糊集重心的模糊综合评判在体育教师教学评估中的应用[J].河南教育学院学报, 2005,14(4):60-62.

[9] 钟诗胜,王知行.基于模糊区间分和模糊重心的决策方法[J].系统工程理论与实践, 1997,17(3):8-15.

[10] 张学东,李新通,章 浩,等.基于模糊重心综合评判的GIS数据产品质量评价研究[J].测绘科学, 2007,32(6):49-51.

[11] 钟诗胜.工程方案设计中的模糊理论与技术[M].哈尔滨:哈尔滨工业大学出版社, 2000.

[12] 何新贵.模糊知识处理的理论与技术[M].北京：国防工业出版社,1994.

[13] 周援衡,王永和,胡 萍.基于模糊集重心理论的软岩分类[J].铁道科学与工程学报, 2011,8(1):48-51.

[14] 吴向明,朱 科,张 楠.田径运动技术特性浅析[J].成都体育学院学报, 1996,22(3):43-45.

[15] 许崇高.田径技术教学法纲要与范例[M].西安：陕西人民教育出版社,1990.