反函数在高等数学中的应用归纳

王 伟 (扬州工业职业技术学院基础部，江苏 扬州 225127)

反函数在高等数学中的应用归纳

王 伟 (扬州工业职业技术学院基础部，江苏 扬州 225127)

从极限、导数、积分、常微分等多方面对反函数的应用进行归纳，同时在较弱的条件下，给出利用反函数求导、求不定积分和定积分的相关定理，改进和推广了相关文献中的结果。

反函数；连续；严格单调；可积

反函数作为初等数学中的一个重要概念，在高等数学中仍起着非常重要的作用。鉴于反函数这一概念的特殊性，文献[1]根据定积分的可积条件与分部积分法推出一种利用反函数求解定积分的简捷方法；文献[2]由换元积分和分部积分法推导利用反函数求解不定积分的方法；文献[3]则通过建立命题、构造反例，对反函数的求导定理进行深入研究，说明定理中的条件不能保证结论成立。笔者在文献[1-3]研究基础上，对反函数的相关定理条件进行适当减弱，改进和推广了相关结果，同时从极限、导数、积分、常微分等多个教学内容，对反函数的例题进行归纳，比较全面地概括了反函数在高等数学中的应用。

1 主要结果

引理1[4]设y=f(x),x∈D为严格增(减)函数，则f必有反函数f-1，且其f-1在其定义域上f(D)也上是严格增(减)函数。

引理2[4]若函数f在[a,b]上严格单调并连续，则反函数f-1在其定义域[f(a),f(b)]或[f(b),f(a)]上连续。

引理3[4]若f为[a,b]上的连续函数，则f在[a,b]上可积。

引理4[4]若f为[a,b]上的单调函数，则f在[a,b]上可积。

定理1设函数y=f(x)在[a,b]上严格单调并连续，若存在y0∈[f(a),f(b)]或[f(b),f(a)]，使得[f-1(y0)]′≠0，则：

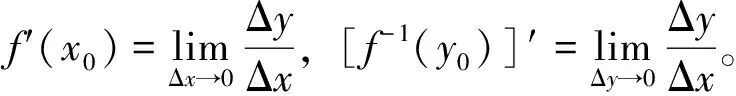
定理2设函数y=f(x)在[a,b]上严格单调并连续，则：

证明根据题意及引理1，2可知，函数y=f(x)存在反函数x=f-1(y)，且x=f-1(y)在[f(a),f(b)]或[f(b),f(a)]上连续，即x=f-1(y)在[f(a),f(b)]或[f(b),f(a)]上存在原函数。

根据分部积分公式，可知：

定理3设函数y=f(x)在[a,b]上严格单调，则:

证明不妨设函数y=f(x)在[a,b]上严格单调递增。此时f(x)的值域即反函数x=f-1(y)的定义域为[f(a),f(b)]，并且反函数x=f-1(y)在[f(a),f(b)]上也严格单调递增。

根据题意及引理1，4可知，函数y=f(x)在[a,b]上可积，其反函数x=f-1(y)在[f(a),f(b)]上可积。

(1)

即：

(2)

此时，可在分割T上选取点集{ξi}={xi-1}，结合式(1)可知：

即有:

又由式(2)，得：

即:

3 应 用

无论是在极限、导数或是积分的教学中，都能看见反函数存在的缩影。下面着重以函数y=arcsinx为例，对高职数学中反函数的应用进行归纳。

例1已知y=arcsinx，求导数y′。

解设y=arcsinx，其反函数为x=siny。根据定理1，可知：

解设y=arcsinx，其反函数为x=siny，则当x=a时，y=arcsina；当x=b时，y=arcsinb。根据定理3，可知：

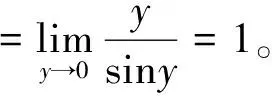
例4求微分方程y′=arcsinx。

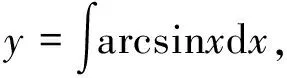
[1]傅湧.反函数求定积分[J].大学数学，2009，6(3)：157-160.

[2]何晓娜.应用反函数求不定积分[J].高等函授学报(自然科学版)，2010，2(1)：40-41.

[3]沈晨，金贵荣.关于反函数求导定理的注记[J].高等数学研究，2007，9(5)：43-44.

[4]华东师范大学数学系.数学分析(上册)[M].第3版.北京：高等教育出版社，2001.

10.3969/j.issn.1673-1409(N).2012.08.057

O171.2

A

1673-1409(2012)08-N172-02

2012-04-23

王伟(1983-)，女，2005年大学毕业，硕士，讲师，现主要从事高等数学教育方面的教学与研究工作。

[编辑] 洪云飞