《圆的周长》教学改进与反思
梁邦林
(仪征市谢集中心小学,江苏 仪征 211400)
[教学内容]
苏教版小学数学第十一册第89-90页内容及例1。
[教学目标]
(1)使学生理解圆周率的意义,理解掌握圆的周长公式,并能正确地计算圆的周长;
(2)通过动手操作,培养学生的观察、比较、分析、综合和主动研究、探索解决问题方法的能力;
(3)通过以圆的周长、直径变化时圆周率保持不变的探索,对学生进行辨证唯物主义的教育;
(4)结合我国古代数学家祖冲之的故事,对学生进行爱国主义的教育。
[教学重点]
推导圆的周长计算公式的过程,正确计算圆的周长。
[教学关键难点]理解圆周率的意义。
[教具]课件。
[学具]
圆形实物3个(大小不等)、直尺、细绳、表格、计算器。
一、教学设计片段
[片段一]
师:你们还记得什么是周长吗?
生:周长就是封闭图形一周的长度。
师:这些图形的周长你们认识吗?请你们选一个图形指指它的周长。
小结:圆也有周长,绕圆一周的长度就是圆的周长。
师:在这些图形里你觉得哪个图形的周长最难求?
生:圆。
师:为什么啊?
生1:因为其他图形是线段围成的,把这些线段的长度加起来就行了。
生2:直的线是可以直接测量的;圆的边是弯的,无法直接测量它的长度。
生3:圆的周长我知道怎样算,直径×圆周率。
(很多学生积极响应:是的,直径×圆周率)
师(不知所措):直径×圆周率?
生 4:对,也就是直径×3.14。
生5:圆周率就是π,等于3.14。
……
【我的困惑:当发现近乎一半的学生已经知道圆的周长计算公式时,我真的有些语无伦次、不知所措了。本来的设计意图是希望从“周长”导入,在激活已有的知识经验的基础上,试图创造矛盾冲突来激发学生自主探究,引出“化曲为直”的思想方法来测量圆的周长,为后面的“猜想——验证”打基础。可现在学生都已知道圆的周长计算公式,如何再创造认知冲突,如何再引导学生动手验证呢】
[片段二]
师:有什么办法来验证一下这个公式到底对不对?
生1:对的,书上就是这么写的!
师:书上写的一定对吗?
生2:老师,我爸就是这么说的。
师:你爸说的一定对吗?那你说说为什么要这样算?
(学生可能感觉到了我的恼羞成怒,不敢再作声。课堂气氛一下子变得凝固起来)
师:要证明圆的周长是不是等于直径乘以圆周率,我们要看一下圆的周长和直径到底有什么关系。这需要我们动手来实验。
(布置实验的内容:测量三个圆片的周长、直径,计算出圆的周长是直径的几倍。学生有些漫不经心,但小组合作似乎缓和了一下课堂气氛)
我发现学生很快就把实验报告单填好了。走进一看,他们都是先在“圆的周长是直径的几倍”这一栏填上3.14,再用3.14乘以圆片上的直径,算出圆的周长。如下表:
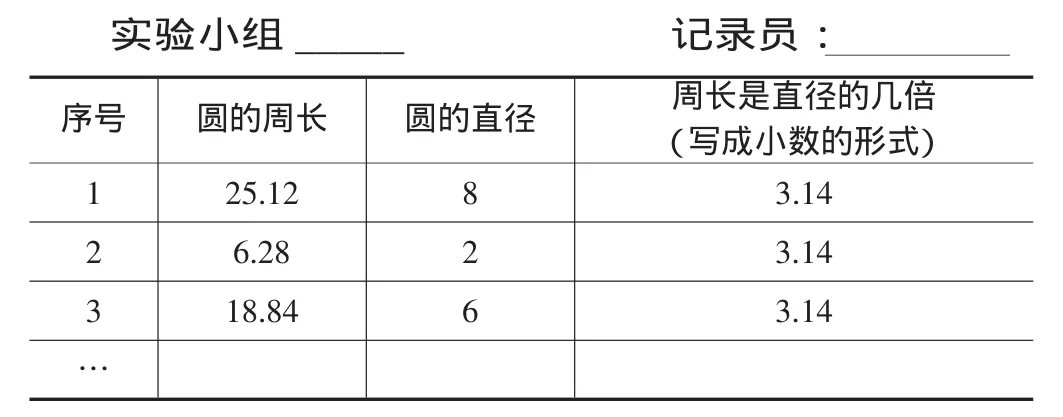
实验小组_____ 记录员:序号 圆的周长 圆的直径 周长是直径的几倍(写成小数的形式)1 25.12 8 3.14 2 6.28 2 3.14 3 18.84 6 3.14…
师:你们是怎么实验的?这个3.14是怎么得到的?
生1:圆的周长本来就是直径的3.14倍啊。
师:现在我们正在验证是不是3.14倍,怎么能直接拿来用呢?
生2:老师,我们算出来刚好都是3.14。
师:是吗?这“周长是25.12厘米”你们是怎么测量出来的?太精确了吧?
……
【我的困惑:这个“猜想——验证”的环节曾被老师们无数次精彩地演绎,在任何一个“圆的周长”教学展示中,这个环节似乎都是必不可少的。为什么到了我的课堂中,学生就不需要验证了呢?他们把动手测量当作是游戏在玩耍,为了堵住我的嘴居然还“睁眼说瞎话”。那么,这个动手验证的环节可以少掉吗?少了这个环节课堂会少掉什么呢】
二、课后反思
(一)课堂上还需要实验验证圆周长的计算公式吗
课后我在班级进行了调查,发现虽然有大部分学生知道了圆周长的计算公式,但他们都不能正确理解圆周率的意义和特征。事实上,研究圆的周长就是在研究圆周率的意义。所以,在课上“动手验证”这一环节是必要的。因为动手验证除了帮助学生知道圆的周长与直径的关系、理解圆的周长计算公式外,还可以培养他们科学实验的意识和观察、归纳等数学能力,可以帮助他们掌握“猜想——验证”的数学学习方法。
但事实上,学生体验不到实验的必要性,不想动手验证,动手验证是我们老师强加给他们的。
在“命令——操作”中研究圆周率,学生内心没有“任务驱动”的心理感应,他们是不会自主地动手验证的。如何让学生在已知圆的周长计算公式的基础上,自发地产生研究“圆的周长与直径的关系”(即圆周率)的需要,是本节课教师需要突破的难点。
(二)实验中圆周率与π值不相符怎么办
事实上,由于多种因素的限制,学生动手验证后得到的值很难与3.14相符,我们该怎样来处理这个矛盾呢?仅仅就说是实验误差吗?好像很难说服学生。而且如果这样处理,那么实验的作用又有什么意义呢?其实这样的测量求证不管怎样减少误差都是很难得到较精确的π值的!我们都知道圆周率的研究经历了数学家们数千年的探索和实验,实现值较精确的突破是刘徽的“割圆术”,而并非我们课堂上所采用的测量方法。
(三)如何让学生体验圆周率是一个固定不变的无限不循环小数
我们的实验结果和学生已有的经验都很难来解释圆周率π是一个固定的数,且是无限不循环小数。我的教学是呈现一些祖冲之的资料后介绍说明圆周率有这一特征,但总感觉是强买强卖的说教。因为学生之前认为圆周率约等于3.14,而实验的数据很难刚好全是3.14,即使刚好是3.14,也很难说明圆周率是固定的数,且是无限不循环小数。我们如何才能帮助学生体验到圆周率是一个固定不变的无限不循环小数呢?
三、教学改进
片段一:创设情境,找准起点
师:我们今天要来研究“圆的周长”。(板书课题)你觉得什么是圆的周长?
生1:绕圆一周的长度是圆的周长。
生2:围成圆一圈的曲线的长度是圆的周长。
师:黑板上画了两个圆,你觉得哪个圆的周长比较长一些?你是怎么想的?
生3:大圆的周长一定长一些。
生4:因为半径长一点,所以它的周长就长一些。
生5:直径长一些,周长也就长一些。
师:要知道大圆的周长比小圆的长多少,你有什么办法?
生6:可以算一算。圆的周长=直径×圆周率,或圆的周长=半径×2×圆周率。
师:什么是圆周率?
生7:圆周率是3.14.
生8:圆周率是π。
生9:不是3.14,3.14的后面还有很多位。圆周率约等于3.14.
师:圆周率可以用希腊字母π表示。那这个公式是用来计算哪个圆的周长?
生9:这两个圆都可以算。
师:操场上的圆呢?或者圆形游泳池的周长呢?
生10:任何圆的周长都可以用这个公式计算。
师:为什么?
生11:因为任何一个圆的周长除以直径都等于圆周率。
师:是吗?不管大圆还是小圆,周长除以它的直径都等于圆周率,也就是约等于3.14,你怎么这么确信?
生11:书上看来的,好像是这样的。
师:你从来都没有怀疑过吗?其他同学呢?
生12:大圆和小圆总有区别吧。
生13:我想也是这样的。但是不敢确定。
【改进说明:一开始先把学生已经知道的全“抖”出来,以便找准学生的学习起点。既然学生知道圆的周长计算公式,却对圆周率不是很清楚,那么我们可以提“为什么这个公式可以计算任何一个圆的周长”“是不是任何圆的周长除以直径都等于圆周率”等问题来激活学生的最近发展区,把他们的思考焦点集中到圆周率上来,他们才会顺其自然地想办法证明:“不管大圆还是小圆,周长除以它的直径都等于圆周率。”如果成立,那么这个公式确实是可以解决任何圆的周长计算问题。研究圆周率的过程就是在研究圆周长计算的本质意义】
[片段二]动手实验,体验探索圆周率的发现过程
师:既然对“任何一个圆的周长除以它的直径都约等于3.14”这一观点有些怀疑,那么我们该怎么办呢?
生1:我们可以找一些圆来实验一下。
生2:先量出这些圆的周长和直径,再计算周长除以直径。
师:量直径是没有问题的,那圆的周长怎么量啊?
生3:可以用绳先绕圆一周,再把绳子拉直进行测量。
师:这个方法可行吗?(课件演示)
师:这种绕绳法你觉得妙在哪里?
生4:把弯曲的圆周长拉直了测量。
师:这种“化曲为直”的办法真的让人赞叹。还有别的方法吗?
生5:可以把圆先做个记号,再在直尺上滚一周,可以测量出圆的周长。(课件演示)
师:我们给这种方法取个名字叫滚圆法。接下来我们小组实验,把材料袋里的学习材料拿出来,有选择地使用。
(学生小组合作,测量、记录有关数据并计算)
【改进说明:学生对于“任何圆的周长除以直径是不是都约等于3.14”这一问题不敢确定,因此激活了他们的探究欲望,使操作验证变成了一种学生自发的需要。在这种需要的驱动下,学生自然能规划实验的过程、能创生“化曲为直”的测量方法,创新精神和实践能力得到了很好的培养】
[片段三]交流类比,感受圆周率的特征
(展示各组实验报告单)
师:仔细观察,大家有什么发现?
生1:圆的周长是直径的3倍多。
生2:每一次的实验数据为什么都不一样?而且没有一个数据是3.14。
生3:因为我们实验的时候有误差。
师:你们的意思是这个倍数的精确程度取决于我们测量的误差大小。如果测量时很精确就会是3.14倍,是吗?
生:是的。
师:老师尽量精确地测量了10次,结果和你们一样,没有一次是3.14,(呈现实验数据)看来这个倍数是不确定的。后来我查了一份资料,我们一起来看一下。(投影资料:中国古代数学名著《周算经》中有“周三径一”的说法)
师:你们有什么想说的吗?
生4:“周三径一”是不是说周长是直径的3倍?
师:是的。你们说是3.14倍,实验数据有没有3.14倍,现在历史资料又说是3倍,到底哪一个对?
生5:不知道。
生6:有点糊涂了。
师:不确定了吧!老师当时跟你们一样很迷惑,怎么办?通过进一步查资料发现,几千年来古今中外的数学家们一直都在研究圆周率。在1700多年前的魏晋时期,我国的杰出数学家刘徽首先指出圆周率不是3!他得出了一个较精确的圆周率的值。他是用什么方法的呢?(投影资料)
师:现在又多出了一个圆周率的值——3.1416,你们相信哪一个?
(此时教师相机介绍千古绝技——“割圆术”)
生7:圆周率等于3是不可能了。
师:那这个3.1416呢?
生:应该对吧,也不肯定。
师:这个数据在当时的条件下已经是非常精确了。
(投影祖冲之相关研究圆周率的资料)
师:看了这些资料,你有什么想说的?
生8:我以前听说过祖冲之,现在发现刘徽也很伟大。中国真是藏龙卧虎!
生9:中国不愧是数学大国。中国人真了不起!
生10:那圆周率到底是几啊?
生11:我们的实验是无论如何也做不到这么精确的。
师:是的。其实还有很多数学家选择了另外的方法在研究圆周率,有兴趣的同学可以去查一下这方面的资料。老师这里还有一份资料。(投影资料)
电子计算机的出现带来了计算方面的革命,1967年圆周率被推算到小数点后2000多亿位,但仍然未算完……后来人们进一步证明了这个数是个固定的数,也是个无限不循环小数。(呈现圆周率小数点后200位)
师:现在你有什么发现?
生12:圆周率是一个无限不循环小数。
生13:圆周率是经过了几千年的研究才发现的。
生14:圆周率是一个固定的数,3.141592653589793 23846……
师:是的,圆周率是一个固定的无限不循环小数。我们为了计算方便,才取它的近似值3.14。现在能回答刚开始时的问题了吗?
生15:任何一个圆的周长除以它的直径都是一个固定的数,但不是3.14。
生16:因为圆的周长与直径的倍数是一个固定的无限不循环小数,所以我们取近似值为3.14。
生17:圆周率是一个固定的数,所以任何一个圆的周长都可以用“直径×圆周率”来计算。
生18:也可以用“半径×2×圆周率”来计算。
……
练习(略)
【改进说明:只有让学生对已知的“圆周率≈3.14”产生怀疑,他们才会关注圆周率到底是多少,怎样可以得到证明的方法。“周三径一”的搅和,把学生的思维推向了另一个起点:除了动手实验外,我们还需要查阅文献资料!使学生深切地体验到,文献研究也是学习的一种重要方式。介绍刘徽和祖冲之的“割圆术”,不仅加强了学生的爱国主义教育,培养了科学探索的精神,而且让他们在了解圆周率研究历史的同时,体验到圆周率是一个固定的无限不循环小数,使他们能自主建构起对于圆周率和圆周长计算的正确理解】

