数学教学中要明白3个为什么

● (台州市第一中学 浙江台州 318000) ● (台州市教研室 浙江台州 318000)

数学教学中要明白3个为什么

●李建明(台州市第一中学 浙江台州 318000) ●蒋荣清(台州市教研室 浙江台州 318000)

近几年中学数学课堂教学的有效性问题备受关注.中学数学课堂到底该实现什么目标，学生在中学数学课堂中哪些方面该得到有效培养，这些在课程标准中都有了明确的要求：一是数学知识与技能的学习；二是在知识的学习过程中把握方法、提升能力、发展意识；三是建立对数学的全面的良好的情感态度价值观.观察目前国内中学数学课堂，在“双基”巩固落实上一直都做得很好，但在思维能力培养上却不尽如人意，有效性的缺失主要表现于此.那么如何更好地弥补这种缺失，进一步提高数学课堂教学的有效性？本文认为关键在于教师在课堂教学中要重视培养学生自主地思考并发问：我想知道为什么？

1 为什么要学习这部分数学知识

刘绍学先生在《普通高中课程标准实验教科书》的主编寄语中就特别谈了“为什么要学数学”的问题，他告诉学生们学习数学的必要性与重要性.事实上，无论是一个模块知识的教学还是一节数学课的教学，都有它存在与出现的必要性与合理性,作为主导者的教师有必要把这个问题在教学开篇之时就向学生交代清楚.学生了解了学习这部分知识的必要性与合理性就能提高学习与钻研的自主性，否则，其积极性与主动性就会大打折扣.

案例1直线的倾斜角与斜率

为什么要定义倾斜角？这是在引入倾斜角这个概念前必须让学生了解的一个问题，也就是让学生了解定义这一概念的目的与意义.为了刻画直线在坐标平面中的位置，为了区别经过同一点的不同直线的位置关系，你会用什么办法？能定义这样的一种量吗？这样的问题引导能让学生明确定义的必要性以及如何定义这个概念.要用角来区别直线位置就需要一个基准、一个参照物，在坐标系内你会找哪个作为参照物？那就是x轴及它的正方向.角是由同一点出发的2条射线组成的图形，结合图形，你会用哪个角来刻画直线的方向？为什么不选与x轴的夹角？这样直线的倾斜角怎么定义就明确了.由于我们的目的是刻画直线的方向,自然直线的倾斜角的范围就应该是0°≤α<180°.为什么不取180°?那是因为它与0°所刻画的是同一种位置状态.为什么不是0°<α≤180°？那是因为能用较小的就不用较大的.这样的引导很自然地让学生了解了为什么要学习这一概念,以及如何定义这一概念是合理的.

至此，对直线倾斜程度的几何、代数这2个方面的刻画都已经完成，但是对它们之间的关系还需要加强理解和认识.教师可以设计如下问题让学生探究：当直线的倾斜角在锐角范围内变化时，直线斜率的变化范围如何？当直线的倾斜角在钝角范围内变化时，直线斜率又如何变化？当直线的倾斜角是0°或90°时，直线的斜率是多少？如果2条直线(不重合)都有斜率，那么这2条直线平行时，倾斜角与斜率有什么关系，反之又如何？

如果教师能在教学过程中不断地引导学生去思考这些问题，那么学习这些数学知识的前因后果就显得既合理又简单，对学生来说也容易接受并乐意接受，不但能感受到学习这些数学知识的必要性，也能感受到“数学是自然的、清楚的”，同时也很好地培养了学生的逻辑思维能力.作为教师，应该把培养学生思考并提问作为教学的一个环节来预设，应该在教学预设中得到体现.

2 为什么会产生这类数学思想方法

教师明白掌握数学思想方法对学生的重要性，也知道数学思想方法的学习不是一蹴而就的，需要在平时的课堂教学中不断进行渗透.同时,很多教师感慨：数学思想方法的教学有效性缺失严重，学生对知识的掌握效率远高于对数学思想方法的掌握效率.这种教学有效性的缺失是不是与教学有关呢？数学思想方法教学的有效性如何才能更好地达成呢？事实上，大量课堂对思想方法的教学都只强调了功能性与重要性，很少说明“为什么会产生这种思想方法”.由于这一根源性问题，学生往往跟着教师体验这种思想方法的神奇，很少领悟为什么会产生这种思想方法，造成了学生在遇到问题时想不到运用该思想方法.

案例2在“平面向量”的复习课上，教师列举了一道2005年浙江省数学高考试题：

例1已知向量a≠e，|e|=1，对任意t∈R，恒有|a-te|≥|a-e|，则

( )

A.a⊥eB.a⊥(a-e)

C.e⊥(a-e) D.(a+e)⊥(a-e)

学生1的思路如下：

由|a-te|≥|a-e|，得

|a-te|2≥|a-e|2,

展开并整理，得

t2-2a·et+2a·e-1≥0.

由t∈R,得

Δ=(-2a·e)2+4-8a·e≤0,

解得a·e=1.故选C.

教师：针对向量模的关系问题，学生1运用平方运算，把模的运算转变为向量运算，并利用方程的判别式得到了正确答案，思路不错，这是我们处理向量模问题常用的方法.大家还有没有其他的处理方法？

图1

(学生沉默.)

教师：其实这个问题还有更好的处理方法，那就是数形结合.

(教师在黑板上画了图1.)

教师：从图1中可以看出，当t的大小变化时，|a-te|也就是向量a-t·e的长度随之改变.而|a-e|也就是a-e的长度是个定值，已知|a-te|≥|a-e|对任意t恒成立，因此|a-e|是所有|a-te|中最小的，那么在什么状态下是最小的呢？显然是垂直状态.

(学生一片惊叹！)

这是中学数学课堂中很典型的一个片段.该教学过程除了让学生对教师的聪明表示赞赏、对数形结合这一方法的功效表示惊叹之外，对数形结合这一数学思想掌握的有效性是不高的，学生们不知道教师是怎么想到，更不知道什么时候用这一思想.

所谓数学思想是对这一数学知识本质的认识，是从某些具体数学内容的认识过程中提炼上升的数学观点，是建立数学和用数学解决问题的指导思想.高中数学中的函数、向量内容是数形结合思想运用的典范.这是为什么呢？这是由这些内容自身的本质特点所决定的：函数与向量都有3种表现形式(函数的表现形式：解析式、图像、表格；向量的表现形式：字母、图形、坐标)，既有代数形式又有几何形态.函数与向量问题的基本形态是符号化的代数形式，将这类代数形态的数量关系用图形语言表现出来，就能更直观形象地感知题目所呈现的问题关系.这就是为什么在函数、向量问题中以形助数思想能发挥关键作用的原因.

3 为什么用这种方法可以解决这个问题

数学教学离不开解题教学，但解题不是教学的根本目的，让学生通过解题教学把握方法、提升思维和分析能力，并在这个过程中培养求知欲、意志力以及理性精神才是解题教学的根本.在解题教学中，很多教师会不遗余力地把自己预设好的解法教给学生，讲得头头是道，学生听得津津有味，解题教学俨然成了解题方法的传授,但是最后在新的问题面前，学生还是无从下手.因为学生从来没有思考过“为什么用这种方法可以解决这类问题”，不能从思维的根源上掌握这一方法，再次遇到时只能凭记忆与经验来解决，数学思维能力培养的长期有效性得不到保证.

(1)求∠A的度数；

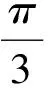
即

因此

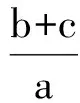
方法2因为a2=b2+c2-bc≥bc，所以

而

故

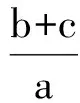
教师在讲解此题时提供了2种思路，一题多解，殊途同归.从学生的反应来看应该都听懂了，但这样的课堂教学给人的感觉就只是“授生以鱼”，其实这里有很多个“为什么”值得学生去思考：方法1为什么能想到利用正弦定理化边为角，为什么化边为角后就能解决问题，为什么要把∠C用∠B替换？方法2为什么使用余弦定理，为什么把所求式进行平方，使用余弦定理后又为什么要运用基本不等式进行放缩？在解决过程中，所有这些问题都必须让学生领悟清楚，只有潜移默化地让学生思考并感知这些“为什么”，才有可能在下一个问题面前快速寻找到思维的突破口.

数学是充满智慧、使人聪明的学科.数学教学在发展学生思维尤其是理性思维方面具有独特的优势和不可推卸的责任.中学阶段是学生理性思维发展和形成的关键期，学生在数学学习的过程中学会把握方法、提升思维能力、发展数学意识，从而建立起对数学全面、良好的情感态度价值观是课程标准对数学课堂教学提出的目标.如果学生在每天的数学课堂教学中都能把上述3个“为什么”作为思考与发问的对象，那么他们就能自觉地、有意识地、充分地体验数学作为理性思维载体的一面，学生的数学思维就能得到较好的培养与提高，数学教学就能为学生的可持续发展奠下良好的基础.

[1] 严士健，张奠宙，王尚志.数学课程标准(实验)解读[M].南京：江苏教育出版社,2004.

[2] 钱佩玲.中学数学思想方法[M].北京：北京师范大学出版社，2001.

[3] 李昌官.让数学教学闪耀理性的光芒[J].数学通报，2006,45(7)：4-7.

[4] 陶维林.利用教学内容的逻辑体系培养学生的逻辑思维能力[J].数学通报，2007,46(2)：26-28.