弱各向异性下晶体生长的相场模型模拟

赵达文

（太原科技大学材料学院，山西太原 030024）

凝固是典型的一级相变过程。在纯物质的凝固过程中，首先通过起伏形成晶核，其后沿着各个方向生长从而形成各种凝固组织。理论分析表明[1，2]，这些生长方向与液固界面上的各向异性密切相关。各向异性是指液固界面的一些物理性质是晶向的函数，常见的有界面能各向异性和动力学各向异性。当各向异性效应较显著时，晶体沿着各向异性决定的方向以枝晶方式生长。在无、弱各向异性条件下不存在优势生长方向，因此各个晶向上都以相同速度生长，当界面曲率半径超过临界值后，会在扰动的作用下发生失稳现象[3]。弱各向异性条件下界面形态演化以及生长方式等都是凝固学的重要内容。对于显著各向异性条件下生长行为已有众多研究报道，而对弱各向异性下生长缺乏相应的研究。

由于数学上的困难，凝固理论无法预测弱各向异性下界面形态演化过程；同时，由于界面各向异性值很难精确测量、各向异性值无法自由调整等原因，导致实验研究也存在较大困难，所以通常用数值模拟方法进行研究。相场模型通过引入序参量场从而避免了显式追踪界面的困难，在凝固组织模拟中得到了广泛应用[5，6]。

本文以自适应有限元方法求解相场模型，分别对界面能和动力学弱各向异性条件下的晶体生长过程进行模拟，从而对其生长规律进行深入研究。

1 相场模型

这里采用Karma等提出的纯物质凝固相场模型[4]。该模型优点是数值求解时保证精度的前提下可以采用较大的界面厚度，并且所引入的网格各向异性远小于传统相场模型。其控制方程由序参量方程和温度场控制方程组成：

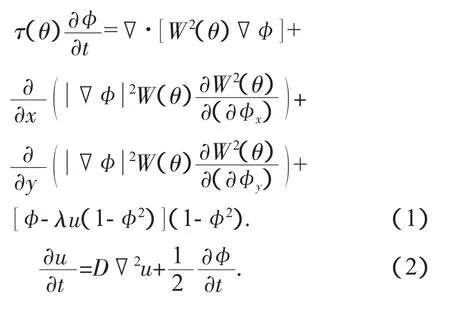
式中：为序参量；u≡（T-Tm）/（L/cp）是无量纲温度；T是热力学温度；Tm是熔点；L是结晶潜热；cp是等压热容；D代表热扩散系数；λ代表耦合常数；θ为界面法线与x轴夹角。τ（θ）为原子弛豫时间，W（θ）为弥散界面厚度，二者分别对应界面能和动力学效应，在不同各向异性条件下有不同形式，具体形式见模拟结果部分。

2 求解方法与计算参数

采用自适应有限元方法求解相场模型，使用自适应网格可以在计算精度不变前提下使求解计算量降低一阶。在空间域上采用伽辽金加权余量法对方程（1）、（2）进行离散，在时间域上分别采用向前差分和C-N格式对二者进行离散，采用ICCG方法求解线性方程。

计算中所采用矩形单元会引入额外的网格各向异性，当各向异性值较弱时，网格各向异性的影响必须予以考虑。计算中采用如下措施来降低网格各向异性影响[5～7]：1）采用薄界面渐近的相场模型；2）采用较小的空间步长；3）通过计算各种参数下的网格各向异性，对所输入各向异性值进行校准。

3 模拟结果与讨论

如上所述，液固界面上常见各向异性有界面能和动力学各向异性。在相场模型中，二者分别体现在界面厚度W（θ）和原子的弛豫时间τ（θ）上。本节中分别对弱界面能、动力学各向异性作用下的晶体生长进行模拟。计算中用到的参数为W0=1.0，τ0=1.0，D=1.0，d0/W0=0.577，△x/W0=0.4，△t/τ0=0.008，无量纲过冷度△=0.65。计算区域大小为409.6W0×409.6W0，初始晶核半径R0=10，计算区域边界为绝热边界条件。

3.1 弱动力学各向异性控制下晶体生长

界面动力学是指液相原子穿过界面最终吸附在固相的过程，在此过程中消耗的驱动力即为动力学过冷。这里设定界面厚度W（θ）各向同性、弛豫时间τ（θ）具有四重对称性

来模拟界面动力学各向异性作用下的生长过程，其中耦合系数λ=5.77.

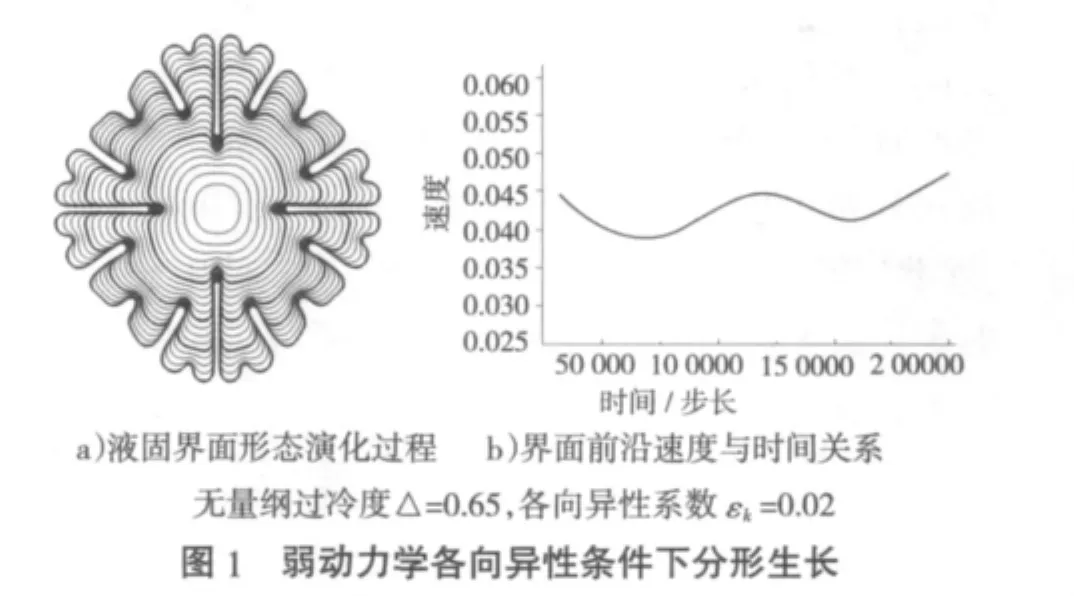
模拟结果表明，当动力学各向异性εk≤0.02时，固相不再以枝晶方式生长。图1a）为εk=0.02时的液固界面形态演变过程，图中轮廓线为间隔1万时间步长的液固界面；图1b）为x轴方向界面前沿的生长速度曲线。在7万步左右时，界面前沿的曲率半径达到极大值，在M-S不稳定性的调制下，界面开始发生分叉（最内侧粗实线）；此时界面生长速度位于第一个波谷位置。紧接着产生分叉。在12万步左右，界面分叉过程已经完成，此时界面前沿的曲率半径达到极小值（图1a）次内侧粗实线）；而V达到第一个波峰位置的极大值。随着生长过程的进行，在16万步左右界面曲率半径再次达到极大值（图1a）中次外侧粗实线），开始第二次分叉过程；此时生长速度V为极小值（图1b）中的第二个波谷位置）。在21万步左右，第二次分叉过程完成，界面曲率半径再次取极小值（图1a）外侧粗实线），生长速度到达图1b）中的第二个波峰位置。可见，随着时间的推移生长前沿重复性的发生分叉现象，生长速度随时间的推移而波动。

3.2 弱各向异性界面能控制下晶体生长

为了单独考察界面能各向异性的影响，这里设定W（θ）=W0（1+εccos4θ），τ（θ）=τ0（1+εccos4θ）2，并通过选择耦合常数λ来消除界面动力学效应。当界面能各向异性系数εc取≥0.02时，固相以枝晶方式生长；而当值εc取0.00001时，晶体不再以枝晶方式生长。图2a）是εc=0.01液固界面演化过程，图中相邻界面时间间隔为1万步；图2b）为x轴附近界面前沿的生长速度。在生长过程中界面前沿周期性的发生分叉，相应的生长速度持续性的波动，同样不存在稳定生长状态。

综合以上模拟结果，可以发现在弱各向异性下具有相同的生长方式：界面前沿总是持续性分叉、生长速度周期性波动、不存在与枝晶生长类似的稳定生长状态。究其原因，是由于在生长过程中由于不存在优势生长方向，使得界面每个位置以相近或相同的速度向各个方向生长；当界面前沿曲率半径大于临界半径值时，在M-S不稳定性的调制下界面失稳发生分叉[3]；当前沿的曲率半径再度超过临界半径时，生长前沿再次发生分叉。通常将这种生长方式称之为分形生长[8]。注意分形生长与有限空间内的doublon生长模式不同[9]，虽然二者的生长形态类似，但是分形生长不存在稳定生长形态和生长速度，而doublon存在稳定生长状态。

4 结 论

使用相场模型对弱各向异性条件下晶体生长进行了模拟。模拟结果表明，在各向异性较弱时固相均以分形方式生长。由于不存在优势生长方向，生长过程中界面前沿总是持续的发生分叉、生长速度周期性的波动，不存在类似枝晶稳态生长的生长状态。

［1］Langer J S，Hong D C.Solvability Conditions for Dendritic Growth in the Boundary-Layer Model with Capillary Anisotropy［J］.Phys Rev A，1986，34（2）：1462-1471.

［2］Langer J S.Recent Developments in the Theory of Pattern-Formation［J］.Physica A，1986，140（1-2）：44-50.

［3］Mullins WW，Sekerka R F.Morphological Stability of a Particle Growing By Diffusion of Heat Flow ［J］.J Appl Phys，1963，34：323-329.

［4］Karma A，Rappel W J.Quantitative phase-field modeling of dendritic growth in two and three dimensions ［J］.Phys Rev E，1998，57：4323-4349.

［5］赵达文.过冷熔体凝固的相场法自适应有限元模拟［D］.西安：西北工业大学，2006.

［6］赵达文，李金富.相场法模拟动力学各向异性对过冷熔体中晶体生长的影响［J］.金属学报，2009，45（10）：1237-1241.

［7］赵达文.自适应有限元方法凝固问题模拟的网格各向异性研究［J］.铸造设备与工艺，2011（2）：20-22.

［8］Johnson B K，SekerkaR F，Foley M P.Scaling of Fractal Aggregates［J］.Phys Rev E.1995，52（1）：796-800.

［9］Brener E，Müller-Krumbhaar H，Saito Y，et al.Crystal-Growth in a Channel-Numerical Study of the One-Sided Model［J］.Phys Rev E，1993，47（2）：1151-1155.