基于Excel的中学数学函数图像教学研究

☆

（如皋高等师范学校，江苏如皋 226500）

一、引言

函数一直是中学数学教学的重点，也是学生最难学习的内容之一。通过函数图像来研究函数的性质，既是数学研究的重要思想，也是数学研究的重要途径。函数图像从“数”到“形”，能够直观、形象、准确、生动地表现函数的性质与参数的关系，通过改变参数，学生可以观察、分析、研究不同参数是如何影响函数图像的，从而总结出函数的相关性质，加深学生对函数及参数意义的理解。因此，准确绘制函数的图像对于辅助函数概念及性质教学具有至关重要的作用。

现代计算机具有非常丰富的图像绘制软件，它们几乎能绘制出所有数学函数的图像。但是，尽管目前可以用来绘制函数图像的软件非常多，可是其中不少软件界面比较复杂，学起来比较困难，操作步骤繁琐，一般教师和学生都很难掌握，不利于掌握和推广。笔者多年从事信息技术与学科教学整合的研究，发现微软办公自动化系列软件中的Excel（本文以Excel2007为操作平台）不仅可以直接根据函数的解析式快速作出静态的函数图像，而且还可以动态地绘制出函数的图像随函数解析式参数的变化而变化的过程，因果关系一目了然。

二、对Excel作图功能的认识

传统的函数图像作图采用的是“描点法”，它的基本步骤是：

（1）列表：根据函数的解析式，按变量大小为序，求出若干个有序实数对填入表中。

（2）描点：即根据列表中的有序实数对，在坐标系中描出对应的点。

（3）连线：将相邻的点用平滑的曲线连接起来即可得到相应函数的图像。很显然，如果要绘制出不同参数情况下函数的图像，那是相当繁琐的。

Excel绘制函数图像的原理实际上也是基于“描点法”的，不过整个过程是由计算机自动完成的，并且能够很好地体现函数图像与参数之间的关系。它的基本步骤是：

（1）在连续的单元格中通过“等差序列”自动生成函数自变量的值。

（2）将函数式改写为相应的公式插入到对应的单元格中。

（3）选择图表类型“无数据点平滑散点图”即可完成函数的静态图像。动态函数图像的绘制就是在静态图像的基础上增加了函数解析中参数的变化，所以，在Excel中需要增加一个区域用来描述函数参数的变化，最后通过动作按钮实现函数图像的动态变化，从而在感官上认识到函数的参数和函数图像之间的关系。

三、Excel与中学函数图像教学的简单整合

在众多的函数中，二次函数y＝ax2＋bx＋c是非常典型的，而且是一个典型的含有参数的函数，不同的a、b、c将决定着这个二次函数的开口方向、开口大小、对称轴、与x的交点情况等性质。因此，通过研究Excel与二次函数图像的有机整合，对于研究其他函数具有普遍的意义。为简便起见，约定其中一个参数变化，而另两个参数不变，这里不妨只考虑“a变化，b、c不变”的情形，以函数“y＝ax2＋2x＋3”为例介绍Excel绘制函数图像的过程。

⒈给定自变量、函数、参数的值

在 A1、B1、C1 单元格内分别输入“x”、“y＝ax2＋2x＋3”、“a”，在 A2 单元格输入－3、A3 单元格输入－2.8，然后同时选中A2、A3这两个单元格，然后将鼠标移到A3单元格的右下角，待鼠标变成“＋”时按住鼠标左键不放，向下填充至数值3为止（这里仅绘制变量x在[－3,3]上的图像，点与点之间的横坐标间距为0.2）。在C2单元格中输入参数a的初始值（这里不妨设为“1”）。在B2单元格中输入公式 “＝＄C＄2*A2*A2＋2*A2＋3”（这里的“＄C＄1”表示参数a的值来源于C2单元格，＄C＄2是绝对地址表示法），从B2单元格向下复制公式，可以得到每一个变量x所对应的函数值。这个过程实际上相当于描点法中的“列表”。

⒉绘制静态的函数图像

选中A列、B列的数据区域，然后执行“插入”→“图表”→“XY（散点图）” →“仅带数据标记的散点图”。这个过程相当于描点法中的“描点”。

将“仅带数据标记的散点图”改为“带平滑线和数据标记的散点图”，可以看到有一根平滑线把这些点连接在一起来，如果选择“带平滑线的散点图”，那么图像上将看不到刚才描的那些点。这个过程相当于描点法中的“连线”，如图1。

图1

改变C2单元格的数值（即改变参数a的值，可以非常清晰地看到图像开口的大小、坐标轴位置的变化等信息。当a为0时图像演变成一条直线）。

⒊绘制动态的函数图像

静态图像不能很好地表现函数图像随参数变化而变化的情况，而动态图像却将这一变化淋漓尽致地表现出来。具体方法：

“开发工具”菜单（如果“开发工具”选项卡未显示，请单击“Office按钮”，然后单击“Excel选项”。在“常用”类别中的“使用 Excel时采用的首选项”下，选中“在功能区显示‘开发工具’选项卡”复选框，然后单击“确定”。）→“插入”→“命令按钮（Activex控件）”→在工作表中绘制一个命令按钮→在命令按钮上右击鼠标，在弹出的菜单中选择“属性”→将“属性”面板中“Caption”右侧框中改为“动画演示”→在命令按钮“动画演示”上右击鼠标→“查看代码”（“开发工具”的“控件”选项中的“设计模式”要处于选中状态，否则“查看代码”一项无法选择）→在“代码”窗口中输入代码：

最后关闭整个“代码”窗口。取消“开发工具”的“控件”选项中的“设计模式”选中状态，单击命令按钮“动画演示”，可以看到参数a由－10变化到10的情况下（每次变化1）二次函数图像变化的情况。

不过，从动画演示的过程中，我们不难发现画面的抖动，这是因为在参数a变化之后，坐标轴也发生了变化，这一点是不利于研究函数图像变化与参数变化之间的关系。为了消除这种抖动，我们需要右击坐标轴，在弹出的菜单中选择“设置坐标轴格式”，在“设置坐标轴格式”对话框中将“坐标轴选项”的“最大值”、“最小值”、“主要刻度单位”、“次要刻度单位”都设定为“固定”，本例中设“最大值”、“最小值”分别为120、－120。再单击命令按钮“动画演示”，可以看到画面非常稳定，学生很容易从动画中观察并得出二次函数图像的开口大小与参数a的关系（a越小开口越大，a越大开口越小） 以及对称性、单调性、顶点位置等函数性质。

当然，如果觉得动画太快，那可以在“DoEvents”与上一行之间加一段延时程序：

注意：可以通过改变“设计模式”的选中与否来决定是编缉命令按钮的程序代码还是执行命令按钮。

四、Excel与中学函数图像教学的高级整合

前面通过仅改变函数的一个参数简单地说明了Excel与函数图像教学整合的过程，下面则以研究三角函数 y＝Asin(ω x＋φ )中的参数 A,ω ,φ 与函数图像的关系进一步阐述Excel与函数图像教学整合的一般过程。

第一种情形：在同一坐标系中作出一个参数取不同值时三角函数y＝Asin(ω x＋φ)的图像及性质（这里不妨只研究参数A变化，而ω和φ不变的情况，其余情况类似。不妨假设ω＝1，φ＝1，此时三角函数就演变成y＝Asin(x＋1)，x∈[－6.2,6.2]）（设 π ＝3.14，为简便起见取 3.1）。

（1）列表。分别在单元格 A1、B1、C1、D1、E1、F1、G1 中输入“x”、“y1＝A1sin(x＋1)”、“y2＝A2sin(x＋1)”、“y3＝A3sin(x＋1)”、“A1”、“A2”、“A3”。在 A2 单元格中输入－6.2，在 A3 单元格中输入－6.0，同时选中 A2、A3单元格后按住鼠标左键拖动“填充柄”到单元格内出现填充值 6.2 为止。在 E2、F2、G2 中分别输入 1、2、3（表示A 分别取 1、2、3这三个数值）。分别在 B2、C2、D2单元格中输入“＝＄E＄2*SIN(A2＋1)”、“＝＄F＄2*SIN(A2＋1)”、“＝＄G＄2*SIN(A2＋1)”。分别选择 B2、C2、D2 单元格向下填充。

（2）描点、连线。选中A、B、C、D的数据区域，然后执行“插入”→“图表”→“XY（散点图）” →“带平滑线和数据标记的散点图”，可以看到有三根平滑线正弦曲线图，如图2。从图中可以非常清楚地发现参数A值越小曲线的振幅越小，A值越大曲线的振幅越大。

图2

改变单元格E1、F1、G1中的数值可以得到A取不同参数值时的图像。

第二种情形：在同一坐标系中运用动画演示不同参数A、ω、φ 下函数y＝Asin(ω x＋φ)的图像。（不妨设π ＝3.14， 为 简便起 见 取 3.1，A∈[－5,5]，ω ∈[－5,5]，φ ∈[－5,5]）。

（1）列表。在单元格 A1、B1、C1、C2、C3 中分别输入“x”、“y＝Asin(ω x＋φ )”、“A＝”、“ω ＝”、“φ ＝”。在A2 单元格中输入－6.2，在 A3 单元格中输入－6.0，同时选中A2、A3单元格后按住鼠标左键拖动“填充柄”到单元格内出现填充值 6.2为止。在 C1、C2、C3中分别输入“A＝”、“ω ＝”、“φ ＝”。在 D1、D2、D3单元格中设置A、ω、φ 的初始值都为1。在B2单元格中输入“＝＄D＄1*SIN(＄D＄2*A2＋＄D＄3)”。选择 B2 单元格向下填充。

（2）在E1、E2、E3单元格中分别插入一个“数值调节钮（Activex控件）”（此控件亦在“开发工具”选项卡），用来调节参数A、ω、φ 的变化。

（3）在“设计模式”下，右击第一个“数值调节钮（Activex控件）”，分别设置此按钮的“max”属性为5，“min”属性为－5，右击第二个“数值调节钮（Activex控件）”，分别设置此按钮的“max”属性为5，“min”属性为－5；右击第三个“数值调节钮（Activex控件）”，分别设置此按钮的“max”属性为5，“min”属性为－5。

设置第一个“数值调节钮（Activex控件）”的控制程序：

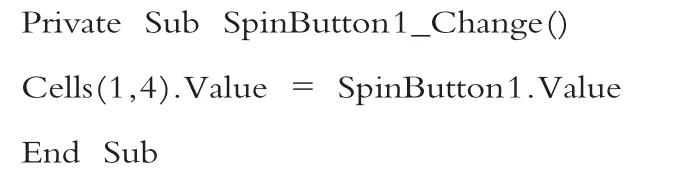
设置第二个“数值调节钮（Activex控件）”的控制程序：

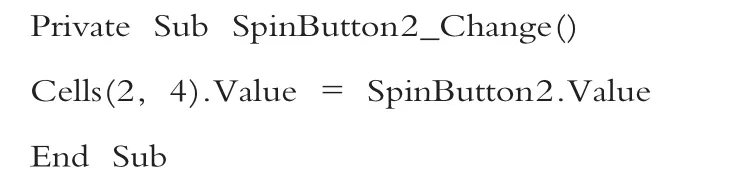
设置第三个“数值调节钮（Activex控件）”的控制程序：

这3段小程序就是将3个“数值调节钮（Activex控件）”分别与D1、D2、D3单元格建立了链接，从而达到通过数值调节钮控制A、ω、φ 的目的。

（4）描点、连线。选中A、B的数据区域，然后执行“插入”→“图表”→“XY（散点图）” →“带平滑线和数据标记的散点图”，可以看到一根平滑线正弦曲线图。

（5）将“坐标轴选项”的“最大值”、“最小值”、“主要刻度单位”、“次要刻度单位”都设定为“固定”，且设“最大值”、“最小值”分别为5、－5。

（6）退出“设计模式”，分别通过“数值调节钮（Activex控件）”来控制参数A、ω、φ 的变化，可以看到函数y＝Asin(ω x＋φ)的图像与参数A、ω、φ 之间的关系，如图3：

图3

实践表明：利用Excel来绘制函数图像不仅简单、方便、易学，而且用它绘制的函数图像非常逼真。中学函数图像教学内容丰富，教师只需向学生演示其中的几个函数图像的绘制并引领他们通过图像来分析、研究、总结这些函数的性质（如单调性、对称性、奇偶性、与坐标轴的交点等性质），而更多的象指数函数、幂函数、双曲线、椭圆等函数图像的绘制、图像的性质分析可以在教师的指导下让学生通过小组协作学习、分组讨论，进而完成学习任务。另外，这些图表中不仅包含了函数图像，而且还包含函数的变量、函数的值，通过数与形的结合，让抽象的函数、图像及性质教学变得简单而直观。这种“实验、探究、发现”教学模式，不仅大大增强了学生学习数学的兴趣，还能够充分培养抽象思维的能力，激发学生学习数学的兴趣，极大地提高学生运用信息技术处理实际问题的能力。

五、结束语

在中学数学教学过程中，用计算机软件绘制函数的图像不仅仅是为了追求视觉上的效果，而是要通过静态及动态函数图像帮助学生对函数的相关知识进行理解，有助于教师引领学生掌握新颖的自主学习方法，对培养学生分析问题、解决问题的能力也大有好处，可以让通过自主学习、协作学习的学生获得新的认知、新的启示、新的发现，进而丰富、拓展学生的认知。

从更深层次的角度讲，将信息技术应用于中学数学教学，使其与中学数学课程教学的有效整合，不仅符合中学数学课程标准，而且符合中学数学课程教学的特点。运用现代信息技术手段，把中学数学课程中丰富、抽象的教学内容，与教师的“教”和学生的“学”进行有机重组从而达到完成课程教学任务的一种新型教学模式。不过，这种整合不是简单地将现代信息技术应用于中学数学的教学过程中，更不是为了“整合”而整合，而是要从真正意义上实现现代信息技术与中学数学课程教学的深度“融合”，它十分强调教师的主导作用和学生的主体地位。它为中学数学的教学创设了新的教学情境，优化了课堂教学的结构，营造了良好的教学氛围，丰富了学科知识,激发了学生参与和探索热情，极大地提高了学生认知能力，它改变了数学及其研究方法，影响了学生学习数学的方式，改变了教师教学数学的模式。

[1]罗朝盛.Visual Basic程序设计教程[M].北京:人民邮电出版社,2009.

[2]杨泽忠.论计算机辅助中学数学函数图像的教学[J].电化教育研究,2002,(9):70－73.

[3]隋新.函数图像解析设计与实现[J].电脑编程技巧与维护,2011,(02):88－89,118.

[4] 孙中红.Excel在数学中的应用[J].计算机与网络,2004,(23):19－20.

[5]何棋.基于信息技术的函数图像对称性探究[J].中小学信息技术教育,2004,(11):41－43.

[6]李胜河.利用Excel讨论函数的有关性质[J].高等函授学报(自然科学版),2010,(03):67,70.