基于Stern-Volmer关系式的压力敏感涂料特性研究
李国帅,范召林,马护生,周 强,熊 健,薛省卫
(1.中国空气动力研究与发展中心,四川 绵阳 621000;2.中国人民解放军94170部队,西安710082)
0 引 言
压力敏感涂料(Pressure Sensitive Paint,PSP)测压技术是一种基于高分子聚合物光致发光过程和动态氧猝灭效应的全域光学非接触式压力测量方法,与常规测压孔测压方法(PSI)相比,其主要的技术优势表现在:(1)可获得表面全域高分辨率的压力连续分布图谱;(2)大大减少了测压孔布置安装所需的成本和工作量,模型制作和试验周期明显缩短,经济性和时效性显著提高;(3)从根本上改变了传统测压方法在模型的薄壁部位或薄壁模型应用的难题,具有较好的适用性。因此,美国、俄罗斯、欧洲、日本[1-9]等国家的气动研究机构和相关大学广泛开展了PSP技术基础和试验研究,使之进入工程应用,并视之为21世纪最有发展前景的试验技术之一。
Stern-Volmer关系式建立了荧光光强与表面压力之间的函数关系,以Stern-Volmer关系式为基础进行相关分析是PSP测压技术的重要研究方向之一。Tianshu Liu[1]等基于温度校正的 Stern-Volmer表达式建立了PSP测压技术不确定度评价分析模型。D.R.Mendoza[2]基于Stern-Volmer关系式通用形式分析了CCD各种噪声对PSP测压精度的影响。Oglesby[3]等从Stern-Volmer基本关系式出发分析了PSP测压技术对压力灵敏度、涂料发光强度的限制。
国内PSP测压技术经过多年的研究已经取得了长足的进展,中航工业集团空气动力研究院、西北工业大学等单位进行了卓有成效的试验研究,为PSP测压技术的工程应用积累了重要经验,但相关基础研究尚未得到广泛关注和深入讨论。压敏涂料是PSP测量的基础,涂料特性的研究对提高PSP测量精度具有重要意义。该研究在推导和整理多种形式Stern-Volmer关系式的基础上,从其衍生式出发,分析研究了测量偏差、压力灵敏度和最佳压力测量范围等主要涂料特性参数的规律特点以及对PSP测量的影响,得出了一些符合PSP测量技术规律并对其工程应用具有重要参考意义的结论。
1 光学压敏涂料测压技术基本原理
PSP测压技术一般通过喷涂方式在模型表面形成功能涂层,将探针分子固定于其中,当涂层受到一定波长激发照射时,其中的探针分子受到激发,进入相应的电子激发态,并通过发射波长更长的光来耗散所吸收的能量,同时与空气中渗透进入涂层并在其中扩散的氧分子相碰撞,转移所吸收的能量,回到基态。上述过程被称为Stern-Volmer过程,而描述该过程的关系式则为Stern-Volmer关系式。Stern-Volmer关系式描述了空气压力与探针分子发光强度之间的定量关系。通过采集有风试验状态和无风参考状态的发光图像,并依据涂料标定实验获得的Stern-Volmer定量关系,就可得到模型表面压力的连续分布。
2 Stern-Volmer关系式
2.1 Stern-Volmer基本关系式
定义压敏涂料光敏探针分子发光量子效率:
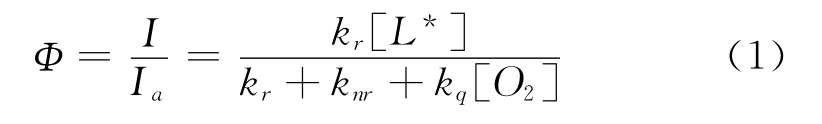
即发光强度和吸收激发光强度之比。
其中:Ia为压敏涂层探针分子吸收激发光光子的能量(强度),I为光致发光过程的发光强度,即发光强度。[L*]、[O2]分别为压敏涂层中激发态探针分子和氧分子浓度,kr、knr、kq分别为辐射能量耗散方式速率常数、非辐射能量耗散方式速率常数和氧猝灭速率常数。
当涂层表面压力为零时,氧分子浓度也为零,不存在猝灭效应:
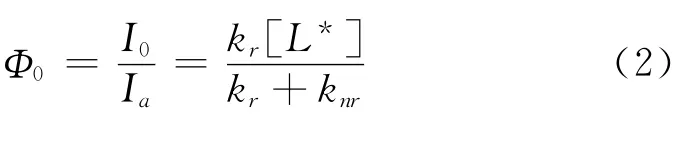
(2)和(1)式做对比,约除不可测量Ia得:
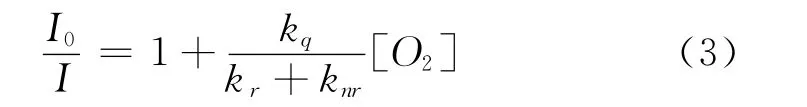
由Hery定律得:

S、P分别为氧分子在压敏涂层中的渗透率(溶解度)和表面压力,φO2为涂层表面气体的氧分压。将(4)代入(3)可得:
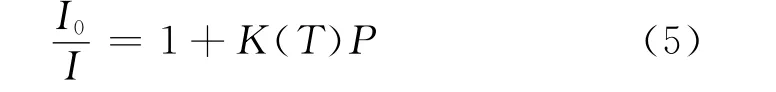
其中:
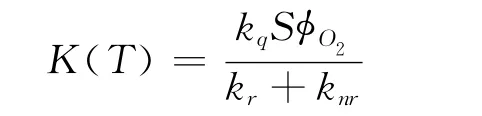
为Stern-Volmer常数,该值受温度影响。
式(5)是Stern-Volmer最基本的形式,式中I0测量较为困难,且测量精度不高,只能作为原理性公式。
2.2 Stern-Volmer线性表达式
工程应用中,一般选择无风(wind-off)状态为参考状态,通过与风洞试验有风状态(wind-on)时的发光强度做比运算来计算模型表面压力。
参考状态下:
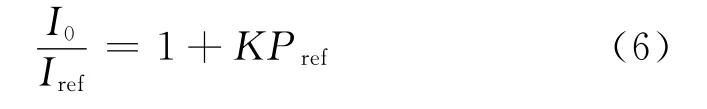
(5)和(6)式做比运算,可得:
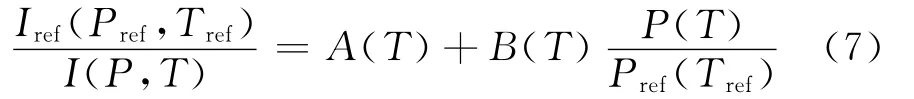
其中:
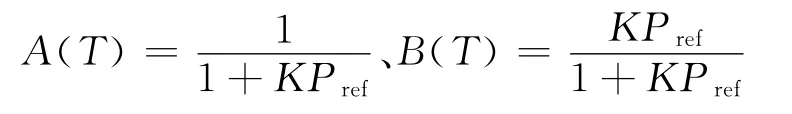
为Stern-Volmer关系式常数,一般由静态标定实验得到,“ref”表示无风参考状态。
式(7)是PSP技术中光强法的基本关系式,是工程中最常用的表达形式,通过无风状态和有风状态发光强度的比运算,可有效补偿甚至消除因涂层厚度、激发光强度和探针分子浓度分布不均匀带来的测量误差。
此外,为了分析处理数据的需要,式(7)经过简单推导,可以得到其它形式:
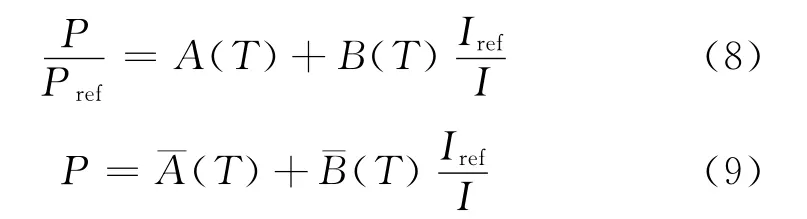
2.3 基于温度校正的Stern-Volmer表达式
温度变化主要影响Stern-Volmer过程中的两个物理过程:无辐射能量耗散及氧分子在涂层中的渗透和扩散。光化学中的Arrhenius[4]和Smoluchowski方程[5]分别建立了温度对无辐射能量耗散速率常数和猝灭速率常数的影响分析模型:
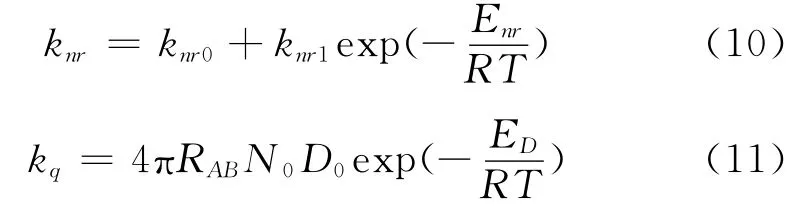
其中:knr0=knr0(T=0),Enr、ED分别为探针分子非辐射能量耗散过程活化能和氧分子在压敏涂层中扩散渗透过程活化能。R为普适气体常数,RAB为光敏探针分子与氧分子之间的平均分子间距,N0、D0分别为阿伏伽德罗常数和氧渗透常数。
将Arrhenius和Smoluchowski方程代入(5)和(7)式,整理计算可得:
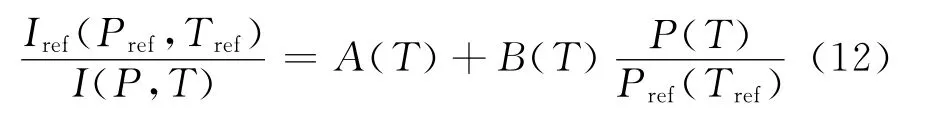
其中:
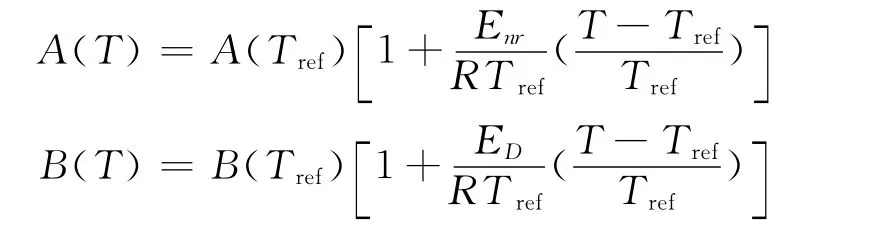
A(Tref)、B(Tref)为T=Tref情况下的 Stern-Volmer关系式常数。
式(12)考虑了温度效应对Stern-Volmer常数影响。通过标定试验可以得到Enr、ED,如果通过红外、TSP等方法得到了模型表面的温度分布,通过式(12)便可以修正温度效应对测压结果的影响。
从式(12)也可以看出,研制低温度敏感度的涂料时应选择Enr较小的探针分子和ED较小的聚合物粘结剂基质材料。
试验研究表明[6]:只要T=Tref,即使温度变化,Stern-Volmer常数基本保持不变,即:
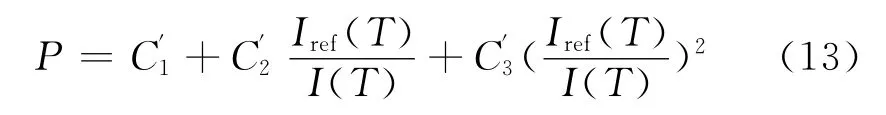
其中系数C′1、C′2、C′3与温度无关。
定义因子K描述有风状态和无风状态之间的温度变化:
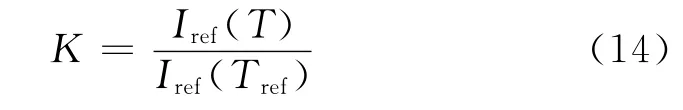
考虑温度效应后的Stern-Volmer为:
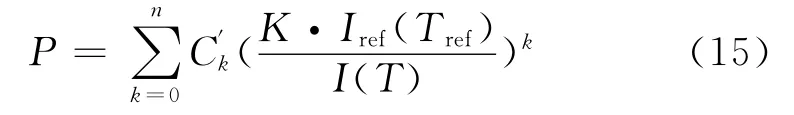
目前,预先标定和原位标定是获得Stern-Volmer常数最常用的方法。当预先标定和原位标定单独使用不能保证校准精度时,通过式(15)可以有效整合两种校准方法的数据信息。
由于模型表面温度分布场的测量较为困难,式(15)在工程中应用更加广泛。
2.4 Stern-Volmer高阶表达式
实验结果表明[7]:线性形式的Stern-Volmer关系式只在有限的压力和温度范围内成立,在更广的压力和温度范围内,一些涂料的Stern-Volmer曲线呈现明显的非线性。
Stern-Volmer关系式的非线性主要因为式(5)的Henry定律没有考虑探针分子在涂层微环境下的异质性以及压力对氧分子浓度和渗透率的影响。
采用更具普遍性的Henry定律[8]:
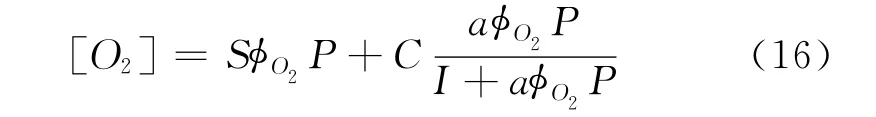
其中:C为Langmuir气体比容,a为Langmuir亲和系数。
将(16)式代入(3)、(7)式,整理推导并进行线性处理可得:
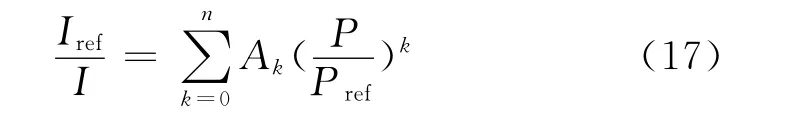
考虑温度效应,将Arrhenius和Smoluchowski方程代入(17)式可得:
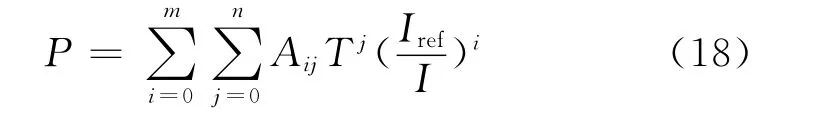
式(17)、(18)给出了Stern-Volmer关系式的高阶形式(一般取到三阶即可保证精度),式(18)还考虑了压敏涂料的温度效应。相比线性形式的Stern-Volmer关系式。式(17)、(18)虽然数据处理较为复杂,但更具通用性,在风洞试验中的应用也越来越广泛。
3 PSP测压技术测量偏差、最优测压范围、压力灵敏度分析
3.1 压力测量偏差分析
定义压力相对测量偏差:

由式(7)可知,PSP测压技术通过探针分子发光强度分布计算压力,压力测量偏差主要取决于发光强度采集误差。
定义探针分子发光效率:

E是压敏涂料荧光强度输出的一个无量纲量度,其测量不确定度ΔE主要取决于相机对灰度的分辨率,8位的标准CCD相机ΔE≈0.5%,16位的科学级CCD相机发光效率的测量不确定度可以控制在0.1%以内。
将式(20)代入式(3)、(7),得:
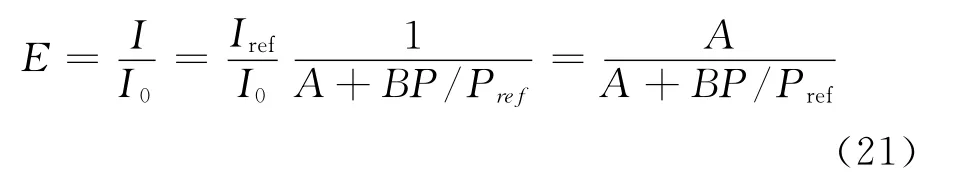
上式求微分,整理可得:
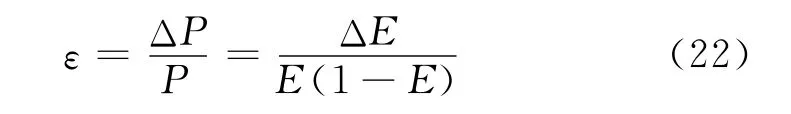
图1描述了ΔE分别为0.5%和0.1%时压力相对测量偏差随发光效率E的变化规律:E=0.5时压力相对测量偏差最小,发光效率E在0.2~0.8之间时,压力相对偏差保持在较低的水平,超出此范围,测量值偏差迅速增大。此外,更小的ΔE可得到更高精度的测量结果,但压力测量偏差随E的变化规律基本不变。
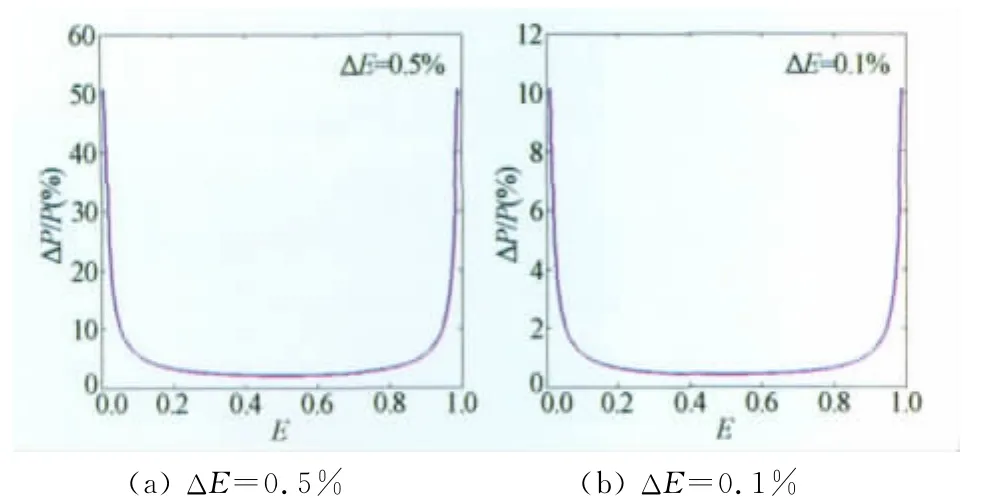
图1 压力相对测量偏差随发光效率变化曲线Fig.1 Relative error in pressure as a function of emittance for constant error in emittance of 0.5%and 0.1%
发光效率E过小,会降低相机的信噪比,发光效率E过大,说明涂料压力灵敏度较低或测量压力较小,会引起较大的相对压力偏差。在涂料研制或工程应用中,应保证压敏涂料在测压范围内发光效率E处于0.2~0.8的水平。
3.2 压力灵敏度分析
定义无量纲压力灵敏度:
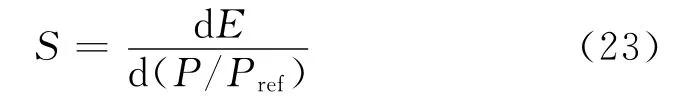
压力灵敏度S表征了发光光强(发光效率)对压力变化响应的灵敏程度。
对(22)式求微分可得:
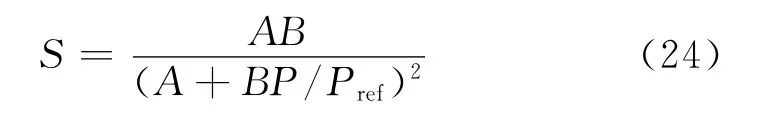
(24)式可转化为:
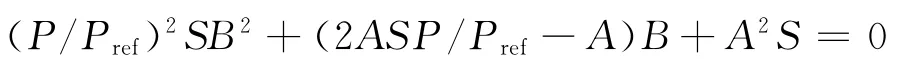
欲使上式有根,则:
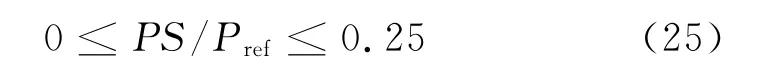
图2给出了对数坐标下压力灵敏度S随压力的变化规律,即压力越大灵敏度越低。
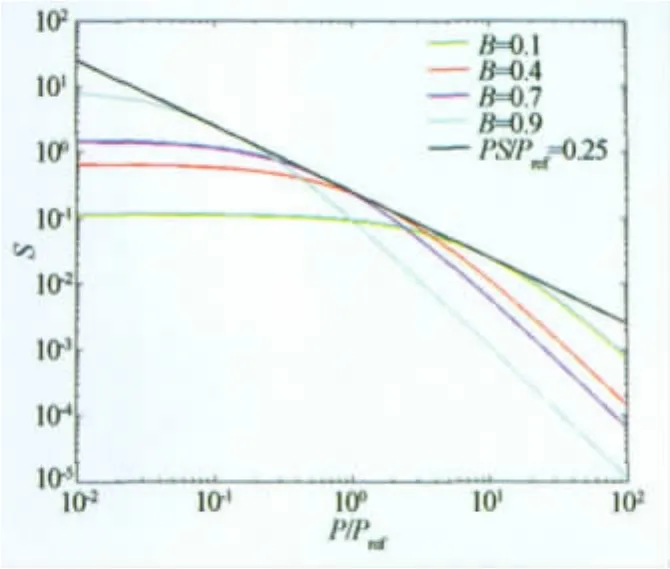
图2 压力灵敏度随压力变化曲线Fig.2 Pressure sensitivity as a function of pressure
由(22)、(23)式易知,图中曲线和极限曲线PS/Pref=0.25的交点对应的压力具有最小的相对测量偏差,可见:不同B值的涂料都有一个压力测量值相对偏差最小的最优压力值Popt,而B值越大最优压力Popt越小。
高B值意味着压敏涂料的高猝灭速率,即高压力灵敏度,但B值过高,大部分激发态探针分子被猝灭,氧分子浓度趋于饱和,相机信噪比变差,这时,压力灵敏度反而会随着B值的增大而变差(如图3所示)。国外工程应用经验表明:跨超声速范围内,B值一般应控制在0.4~0.8[5]。
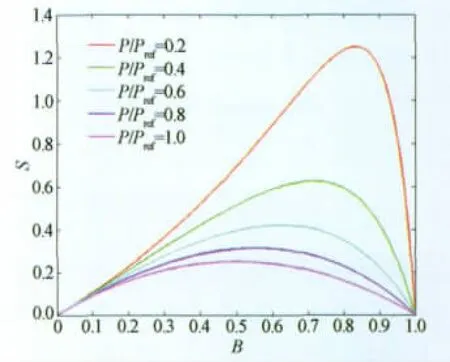
图3 压力灵敏度随B值变化曲线Fig.3 Pressure sensitivity as a function of B
3.3 最优测压范围分析
联立(21)和(22)式可得:
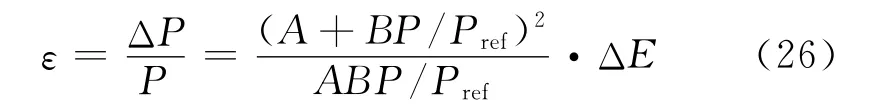
对(26)式求微分,可得:
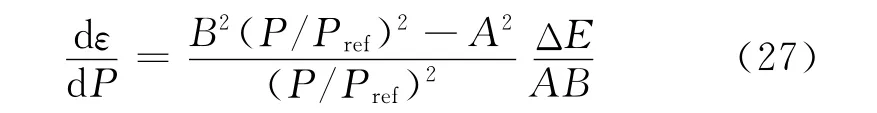
图4给出了不同B值下压力测量值相对偏差随压力的变化规律。由图4可知,存在着使压力测量值相对偏差最小的最优压力值Popt,Popt以外的压力范围内,测量值相对偏差迅速增加,尤其在低压段;另一方面,B值越大Popt越小,对于提高低压段测量精度更为有利,但高压段测量精度变差,最优测压范围也越窄。在涂料研发与工程应用中应平衡压力灵敏度与压力最佳测量范围之间的矛盾。
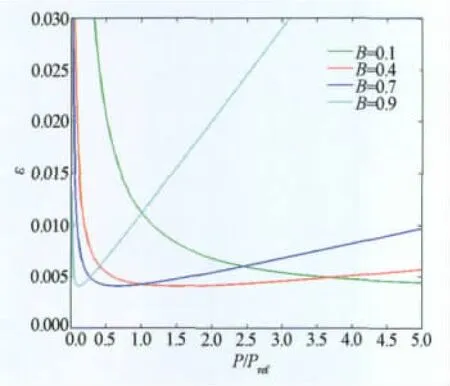
图4 压力相对测量偏差随压力变化曲线Fig.4 Relative error in pressure as a function of pressure for different Stern-Volmer constants B
由式(27)易知,当Popt=A/B=1/B-1时,压力相对测量偏差最小,且最小值为:

显然,压力测量值相对偏差与ΔE成正比,对于16位的CCD相机,最小测量值相对偏差可低至4‰。因此,工程应用中,应根据试验条件、设备技术性能来选择合适的涂料配方,尽量选择最佳压力范围附近的配方,以保证测量精度。
需要说明的是,上述分析仅基于PSP技术的基本原理,没有考虑诸如光降解、光源稳定性、模型移动和变形等的影响。
4 结 论
研究结果表明:
(1)Stern-Volmer关系式具有多种表达形式,在工程应用中,应根据实际情况选择相应的形式;
(2)涂料的发光效率E应控制在0.2~0.8之间,以确保较低的压力相对偏差;
(3)B值是表征压敏涂料压力灵敏度的参量,B值越大,表明涂料的压力灵敏度越高,但涂料最优测压范围也越窄,筛选涂料配方时应综合考虑上述两方面因素;
(4)Popt=1/B-1时压力测量精准度最好,工程应用中,应预估表面压力变化范围并选择最佳压力测量范围与之匹配的涂料配方;
(5)最小压力相对偏差为εmin=4ΔE,通过提高相机动态范围、改善相机信噪比等方法可以有效提高测量精度。
[1] TIANSHU Liu,GUILLE M,SULLIVAN J P.Accurancy of pressure sensitive piait[R].AIAA 99-33734,1999.
[2] MENDOZA Donald R.An analysis of CCD camera noise and its effect on pressure sensitive paint instrumentation system signal-to-noise ratio[C].Pacific Grove,CA,Sept.29-Oct.2,1997.
[3] DONALD M.Oglesby.Optimization of mesurements with pressure sensitive paints[R].NASA TM-4695,1995.
[4] SONG L,FAYER M D.Temperature dependent intersytem crossing and triplet-triplet absorption of rubrene in solid solution[J].Journal of Luminescence,1991,50:75-81.
[5] KALYANASUNDARAM K.Photochemistry of polypyridine and porphyrin complexes[M].New York:Academic Press,1992.
[6] HUBER J P,CARROLL B F.Application of dual sorption theroy to pressure senitive paints[J].AIAA J.,1997,35(11):1790-1792.
[7] TARUN Dhall,CENGIZ Chall.Pressure resolution of a PSP based measurement system with non-linear intensity response[R].AIAA 2008-279,2008.
[8] WOODMANSEE M A,DUTTON J C.Method for treating temperature-sensitive effects of pressure-sensitive paints[R].AIAA 97-15451,1997.

