板桩码头结构中桩体作用宽度试验研究
徐光明,李士林,刘永绣,吴荔丹
(1.南京水利科学研究院,南京 210029;2.水文水资源与水利工程国家重点实验室,南京 210029;3.中国水电顾问集团贵阳勘测设计研究院,贵阳 550008;4.中交第一航务工程勘察设计院有限公司,天津 300222)
1 研究背景
板桩码头结构以其结构形式简单,造价低廉,施工周期短等独特优点,在国外众多港口码头建设中得到广泛的应用[1-2],由于长期缺乏用于建造前墙的优质型钢,我国板桩码头结构仅用于中小型港口工程。自2000年以来,钢筋混凝土地连墙板桩码头结构设计水平和施工技术得到极大提升,遮帘式板桩码头结构和卸荷式板桩码头结构等具有自主创新特色等板桩结构型式在多个大型深水泊位建设中得到成功应用[2]。现有的板桩码头结构的设计计算理论已不能完全满足当前大吨位深水板桩码头的设计建设要求,因此,为完善板桩码头结构的设计计算理论开展了专题研究。在板桩码头结构中,桩是一种最常见的构件,如斜拉板桩码头中的斜拉桩,遮帘式板桩码头中的遮帘桩,由于它们抵抗地基侧向变形和横向作用荷载,因而具有显著的遮帘作用。但如何在码头结构设计计算中考虑这种遮帘作用,一直是大家关注的问题,而问题的关键是了解单根桩体的作用宽度的计算。在全遮帘式板桩码头设计计算中,为了考虑由于土体之间和土体与遮帘桩之间的摩擦而产生的拱效应,就将遮帘桩承受陆侧土压力的作用宽度扩大,假设作用宽度约为遮帘桩桩宽的2倍[2-3],然而这一做法的合理性急需验证。针对这一问题,本文采用土工离心模型试验手段,在南京水利科学研究院400 g-t土工离心机上开展了多组模型试验,设计布置了简易的板桩码头结构模型,模拟了6种不同间距的桩排结构情况,测量各种情况中桩体前后两侧的土压力分布,通过分析计算这些模型中桩体在港池开挖后所承担的总土压力,进而分析桩排中单根桩作用宽度随桩间距的变化规律。
2 土工离心模型试验
2.1 试验原理
土木工程师很多年前就尝试通过小比尺的物理模型来研究岩土工程问题,然而一直未取得理想的研究成果。这是因为土的力学特性又是随应力水平不同而表现不同,而在岩土工程中,土体自重引起的应力是最主要的应力,若在地面上1 g(g为重力加速度,等于9.8m/s2)条件下对缩尺1/N的物理模型进行试验(N为模型长度比尺),土体和其中的结构物中的自重应力水平仅为原型的1/N,远远低于原型实际工程中的自重应力水平,模型的性状就不能很好地反映原型的性状。所以,开展真正有价值的土工物理模型试验研究,首先必须使模型中的土体和其中的结构物的应力水平与原型相等。满足这一前提条件的有效途径之一就是将模型置于高速旋转的离心机中,使1/N缩尺的模型承受N·g离心加速度的作用,此受力环境称N倍重力加速度的超重力场。这样,模型土体和其中的结构物中的应力水平就等同于原型中的应力水平。换言之,土工离心模型试验优于常规土工模型在于借助离心机的高速旋转,为模型创造一个与原型应力水平相同的应力场。
目前,土工离心模型试验技术作为一种有效的物理模型试验方法,几乎涉及土木工程的所有领域,成为岩土工程技术研究中最先进、最主要的研究手段之一。近几年来,土工离心模型试验技术在港口工程的设计研究、方案选型和机理探寻等方面发挥了积极的技术支持和推动作用,产生了良好的社会效益和显著的经济效益[2,4]。
2.2 相似准则
以质量M、长度L、时间T作为基本物理量,假定几何比例尺N为原型几何长度与模型几何长度之比,根据几何相似条件和力学相似条件,推得原型与相似模型的主要物理量比例尺见表1。
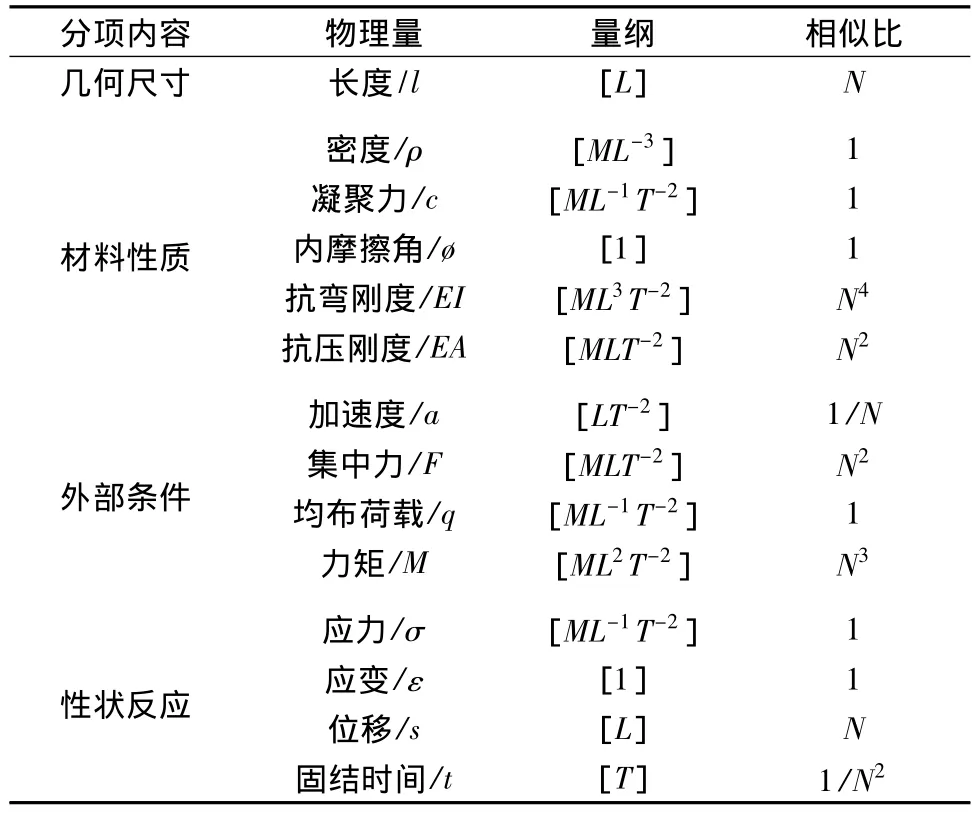
表1 模型与原型相似时的主要物理量比例尺Table 1 Similarity scales of main physical variables between model and prototype
3 模型试验
3.1 试验设备和模型几何比例尺
离心模型试验是在南京水利科学研究院NHRI 400 g-t大型土工离心机完成[5]。该机的最大半径为5.5 m,最高离心加速度200 g,相应最大负荷为2 000 kg,容量达 400 g-t。
虚拟的原型码头结构情况为,前墙高16 m、厚300mm,墙前港池深8 m;墙后布置一排矩形截面桩,桩长16 m,截面厚810mm,宽450mm。试验所使用的平面应变模型箱净空尺寸为1 000mm(长)×400mm(宽)×1 000mm(高)。综合考虑后,选定的长度比例尺为30,即N=30[5]。
3.2 模型前墙和桩体
一般来说,土工离心模型中所有材料应该选用与原型相同的材料进行制作。原型板桩结构码头中的前墙和桩体为钢筋混凝土材料,按长度比例尺N=30缩制的这些模型结构件,其断面尺寸都很小,若它们仍采用钢筋混凝土制作,细部结构尺寸难以精确控制,模型测量也相当困难,因此,这里采用铝合金材料替代混凝土材料制作这些模型前墙和斜拉桩。
在桩板桩码头结构中,前板桩墙和桩体属于抗弯构件,因此,这些模型均按等抗弯刚度相似原理进行设计计算。在宽度方向,即与受弯平面相垂直的方向,仍按长度比例尺缩制构件,即bp=bmN,在受弯平面内,需满足
对于前板桩墙,模型墙体厚度按下式计算,

式中:下标m,p分别代表模型和原型;E为材料弹性模量;I为截面惯性矩,即I=bD3/12,D为墙体厚度。
已知铝合金板Em=70 GPa,钢筋混凝土Ep=28 GPa,前板桩墙厚度Dp=300mm,N=30,计算出模型前墙厚度Dm=7.4mm;模型墙板的宽度就取模型箱的宽度bm=400mm,相对应的原型宽度bp就是12.0 m;而前墙高度hm=16 000/30=533.3mm,因此,模型前墙的尺寸为533.3mm×400mm×7.4mm。同理算得的模型桩尺寸为533.3mm(长)×20mm(厚)×15mm(宽)。
为模拟这些原型钢筋混凝土结构物的表面粗糙度,在模型构件布置好测试元件后,在其表面用环氧树脂胶粘贴一层粉细砂颗粒,以达到增糙的目的。
3.3 模型地基
为了取得较为理想的研究结果,尽量让模型地基条件均匀一致,选取河北省曹妃甸港区的一种均质细砂作为模型地基土料,具体级配为:粒径大于0.25mm占1.9%,粒径介于0.25~0.075mm 占92%,粒径大于0.075mm占6.1%。这种砂的土粒相对质量密度Gs为2.67。按同一相对密度(ID=0.41)作为控制标准进行制备,形成地基土层。首先将细砂土料自然风干,然后借助多孔砂漏斗,采用砂雨法将其成层撒落在模型箱内,在由下而上制备过程中,始终保持落高相同,以控制模型地基土层上下密度均匀一致。模型地基层的主要物理力学特性见表2。

表2 模型地基土的物理力学特性Table 2 Physical and mechanical features of model soil ground
3.4 模型测量
试验采用的土压力传感器是特别为土工离心模型试验开发研制的界面土压力盒,有BW-3型系列和BW-4型系列2种微型土压力盒[6]。BW-3型土压力盒外径16mm,厚4.8mm,量程分 200,300,400 kPa,它们布置在前墙挡土侧以及海侧的泥面以下部分的墙面测点处,与墙面齐平,上下测点间距离相等;BW-4型土压力盒外径11mm,厚4.3mm,量程分200,300,400 kPa,它们布置在桩体前后两侧表面,埋设后与桩表面齐平,上下测点间距离相等。
3.5 模型设计和试验步骤
如前所述,这些模型所模拟的原型实为一种简单的板桩码头结构,挡土结构由前墙和一排工作桩组成。前墙上端与码头地基表面齐平,对应原型标高0.0 m,前墙海侧前沿泥面对应原型标高-8.0 m,因此,挡土高度为8.0 m。与前墙相距3.0 m设有一排桩,其上端与一根水平系梁相联结。为了分析出一排桩中单独一根桩的土压力作用宽度随桩间距的变化规律,这里设计了8组模型试验,包含6种桩间距,其试验情况见表3。

表3 桩体作用宽度模型试验总表Table 3 Designs of model tests on equivalent breadth of pile
模型制作和试验过程如下,如图1(a)所示,地基土为均质细砂,用砂雨法向模型箱内撒砂直至至图中标高-16.0 m位置时,将模型前墙和工作桩置于指定位置,暂时固定好。然后,继续撒砂至标高0.0 m所在位置面。需要说明的是,考虑到砂雨法制备的细砂地基在原型自重应力作用下要发生一定数量的压缩沉降,因此,实际形成细砂地基面要高出标高0.0 m面约15mm。

图1 模型剖面布置Fig.1 Layout of model cross-section
将制备好模型移入离心机吊篮平台,在30 g离心加速度运转条件下,让模型地基承受对应原型的自重应力作用,同时也让地基土体与前墙和工作桩充分接触。
这一过程之后,停机移出模型,在前墙海侧开挖至图中标高-8.0 m所示的泥面,形成模型港池,如图1(b)所示。由于在原型自重应力作用下,前墙陆侧地基土体侧向变形,前墙向海侧移动,若不给墙后工作桩在水平向施加任何约束,工作桩也随之向海侧移动,因而起不到遮帘挡土的作用,因此,模型CM1至CM6在港池形成后,均通过系梁给工作桩施加了水平约束,如图1(b)所示。
再次将模型移入离心机,开启离心机,升速至30 g离心加速度运转,让模型前墙和其陆侧的工作桩承受水平向土压力的作用。通过前墙和工作桩上预埋的微型土压力盒和粘贴的弯矩测量单元,观测它们的工作性状,特别是观测工作桩海陆两侧的土压力分布,从而分析出单根桩的作用宽度。
对于不同的模型,所模拟的原型工作桩间距各不相同,桩间距从小到大共有6种,这样,桩间距d与桩宽 b 之比(d/b)也有6 种,即1.0,2.0,3.0,4.0,8.0和13(表3),图2给出了模型CM2至CM5的平面布置情形。
表3所列的模型CM7和CM10,是完全相同的2组重复性模型,它们的布置与模型CM6完全相同,由于墙后桩排中的桩净间距为零,整个一排桩就连成了一道工作墙,在模型中用铝合金板制作,换言之工作墙是桩间距与桩宽之比等于1(d/b=1)的一种特殊情形。但模型CM6的工作墙顶端施加有水平向约束,而模型CM7和CM10的工作墙顶端无约束。在模型CM7中,对工作墙两侧的土压力进行了测量,而在模型CM10中,对前墙两侧的土压力进行了测量。通过比较前墙与工作墙两侧的土压力分布,用来说明工作墙顶端水平向约束作用。

图2 模型平面布置(CM2-CM5)Fig.2 Plane layout of the model(CM2-CM5)
4 试验结果分析
在分析模型CM1至CM6试验结果之前,先分析一下模型CM7至CM10的试验结果。图3给出了在30 g运转条件下模型CM7的工作墙和CM10的前墙两侧的土压力分布比较,可见,前墙和工作墙的陆侧土压力分布几乎一致,同时前墙和工作墙的海侧土压力分布也非常接近,由此表明,顶端无约束的工作墙没有起分担前墙土压力的作用,可见,设置工作墙或工作桩时,若顶端无水平约束,它几乎不起作用。换言之,要使板桩码头结构中桩构件发挥作用,必须给桩体提供足够的水平约束。这一试验结果说明了模型CM1至CM6中工作桩或工作墙顶端设置水平约束的必要性。

图3 无约束情形中工作墙和前墙两侧土压力分布Fig.3 Distribution of pressures on both sides of front wall and retaining wall without restraint
我们知道,工作桩或工作墙的两侧土压力分布相同时,两侧没有压力差,就不承担任何侧向荷载,但当其两侧土压力分布不完全相同,即海陆两侧有压力差时,说明它承受侧向荷载,发挥抵抗土体侧向变位的作用。
这样,在分析不同间距情况下桩排中的单根桩作用宽度系数,只要计算工作桩两侧的总土压力,即土压力沿桩侧的合力。对于工作墙,则计算宽度取单桩宽度即可;然后,求出两侧总土压力差;最后,拿各种情形的总土压力差与工作墙情形相比较,即可知道单根桩作用宽度系数。由于计算总土压力时的积分高度会影响到单桩作用宽度系数的分析结果,这里积分高度统一为从码头面标高至泥面标高,即计算高度为标高0.0至标高-8.0 m之间桩体。
设pf,pb为桩体或墙体海陆两侧土压力沿深度z方向的分布,Pf,Pb为海陆两侧的总土压力,H为自码头面标高至泥面标高的挡土高度,d,b分别为工作桩的间距和宽度,则桩排中的单根桩作用宽度系数keq计算表达式如下,

图4至图9是各种桩排情形中单根工作桩两侧土压力分布结果,据此按公式(2)计算出的单根桩作用宽度系数keq值,该值已列入表3。显然,keq值是桩排中桩的间距宽度比d/b的函数,实测关系分布见图10。

图4 模型CM1工作桩两侧土压力分布Fig.4 Distribution of pressures on both sides of the pile in modelcm1

图5 模型CM2工作桩两侧土压力分布Fig.5 Distribution of pressures on both sides of the pile in modelcm2

图6 模型CM3工作桩两侧土压力分布Fig.6 Distribution of pressures on both sides of the pile in modelcm3

图7 模型CM4工作桩两侧土压力分布Fig.7 Distribution of pressures on both sides of the pile in modelcm4

图8 模型CM5工作桩两侧土压力分布Fig.8 Distribution of pressures on both sides of the pile in modelcm5

图9 模型CM6工作桩两侧土压力分布Fig.9 Distribution of pressures on both sides of the pile in modelcm6

图10 单根桩作用宽度系数与桩间距桩宽比Fig.10 Correlation of the equivalent breadth ratio of one pile with the ratio of space to breadth
从图10可以看到,当桩的间距宽度比d/b由1.0逐渐变大到 4.0,keq值由1.0增大至3.0,两者近似呈线性增长关系,之后,单根桩作用宽度系数值不再随着d/b值增大,而逐渐趋于常值,稳定在3.0上下。这样,可以用2段折线近似反映值与d/b之间的变化关系,如图10所示。首先,当d/b=2.0时,即桩与桩之间的净间距等于桩宽这一情形,按照这一近似关系曲线推测的单根桩作用宽度系数值约1.6,但小于2.0。其次,当d/b 大于4.0之后,值不再随d/b明显增长,因此,较为经济的布桩间距可达4.0。
5 结论
通过8组大型土工离心模型试验,对桩体作用宽度这一基础性问题进行了分析研究。初步试验研究结果表明:①板桩码头结构中的工作桩必须在水平约束条件下,才能发挥承担水平向土压力的作用;②桩排中的单根桩作用宽度系数keq与桩间距宽度比d/b关系密切,两者关系曲线近似呈折线分布。当d/b由1.0增大至4.0,keq值相应从1.0增大至3.0;之后,keq值逐渐趋于常值,不再随着d/b值出现大的波动。因此,较为经济的布桩间距可达4.0。对于d/b=2.0这一情形,实测到的单根桩作用宽度系数keq值约1.6,不足2.0。
[1]TSINKER G P.Handbook of Port and Harbor Engineering:Geotechnical and Structural Aspects[M].New York:ITPInternational Thomson Publishing,Chapman&Hall Press,1997.
[2]刘永绣.板桩和地下墙码头的设计理论和方法[M].北京:人民交通出版社,2006.(LIU Yong-xiu.Design Theory and Methods of Bulkhead of Sheet-Pile and Concrete Diaphragm Wall[M].Beijing:China Communications Press,2006.(in Chinese))
[3]JTJ 292-98,板桩码头设计与施工规范[S].北京:人民交通出版社,1998.(JTJ 292-98,China Code of Design and Construction of Sheet-Pile Bulkhead[S].Beijing:China Communications Press,1998.(in Chinese))
[4]蔡正银,李景林,徐光明,等.土工离心模拟技术及其在港口工程中的应用[J].港工技术,2005,168(增1):47-50.(CAI Zheng-Yin,LI Jing-lin,XU Guangming,et al.Centrifugal Simulation Technique of Soil Mechanics and Its Application to Port Engineering[J].Port Engineering Technology,2005,168(Sup.1):47-50.(in Chinese))
[5]徐光明,蔡正银,李士林,等.《板桩码头设计与施工规范》修订斜拉板桩码头结构力学特性离心模型试验研究报告[R].南京:南京水利科学研究院,2007.(XU Guang-ming,CAI Zheng-yin,LI Shi-lin,et al.Research Report of Centrifuge Model Test on Behavior of Structure of Sheet-Pile Bulkhead with Raked Piles Conducted for Revision of China Code of Design and Construction of Sheet-Pile Bulkhead[R].Nanjing:Nanjing Hydraulic Research Institute,2007.(in Chinese))
[6]徐光明,陈爱忠,曾友金,等.超重力场中界面土压力的测量[J].岩土力学,2007,28(12):2671-2674.(XU Guang-ming,CHEN Ai-zhong,ZENG You-jin,et al.Measurement of Boundary Total Stress in a Multigravity Environment[J].Rock and Soil Mechanics,2007,28(12):2671-2674.(in Chinese))

