软土地区新建盾构隧道下穿越既有隧道的离心模拟研究

马险峰，何蔺荞，王俊淞

(同济大学a.岩土及地下工程教育部重点实验室;b.地下建筑与工程系，上海 200092)

随着我国城市建设的高速发展，居住人口持续快速增长，城市市区可利用的地面面积越来越少，从而带来了诸如交通阻塞、空间拥挤等一系列问题的“城市综合症”。为了促进城市的可持续发展，改善城市形象，开发地下空间自然而然成了解决这些问题的有效途径，因此，修建地铁、地下通道日益受到政府的重视。习惯上将新建结构物临近既有结构物施工，并可能对既有结构物产生不利影响的工程称为近接工程。近接工程中，盾构近距离穿越施工是首当其冲的。随着地铁网络不断完善，新建隧道近距离穿越已建隧道及其他各种地下构筑物的现象也是越来越多。上海地区地铁线路密集，常会遇到新建盾构隧道近距离穿越既有隧道的情况，例如:地铁二号线人民广场段下穿越地铁一号线工程;越江观光隧道上穿越地铁二号线工程;地铁八号线人民广场段上穿越二号线工程;地铁十号线豫园站至南京东站下穿越二号线工程;西藏路大型泥水盾构下穿越地铁八号线工程;外滩通道工程近距离上穿越地铁二号线工程等。

新建盾构隧道施工不可避免地会引起周围土体的扰动，改变土体应力状态，引起地层位移及地表沉降。特别是富水的软塑或流塑土层中，施工扰动会导致土体强度及压缩模量降低、孔隙水压力升高，这必然会引起长期的固结及次固结沉降。当地层变形超出一定范围时就会危及临近建、构筑物的安全，引起一系列环境岩土问题，甚至引起灾害事故［1］。近年来，由于周围条件限制及规划设计的影响，隧道穿越的间距也越来越近，使得穿越工程难度大、风险高。在盾构近接施工中，单孔及水平平行隧道的相关技术巳经趋于成熟，但是对于近距离施工的交叠穿越的地铁隧道而言，由于隧道间的相互影响使之较水平平行隧道在施工上更难于控制。因而，对盾构隧道近距离交叠穿越的研究显得尤为必要。

1 研究背景

目前，对于新建盾构隧道，近距离穿越施工对既有隧道结构的影响这一课题的研究，主要采用数值计算和实测数据分析方法，只有少数学者进行过模型试验研究。一方面，由于土体性质的不确定性以及周围环境的复杂性，研究主要集中在数值计算和监测方面，无论是从系统性还是深度来说，都还不够深入。另一方面，已建成并正在运营中的地铁隧道对变形的要求极其严格，对于现在出现的新型问题的设计和施工还没有规范、标准可循。因此，广泛、深入、系统地研究新建盾构穿越施工对已建隧道的影响，对盾构隧道技术的发展及深层地下空间的开发利用具有重要意义，在工程实践中将创造巨大的社会、经济效益。

Kim(1996)［2］、周文波(2000)［3］、俞涛［4］、何川(2008)［5］等人根据不同的理论假设和不同的具体试验方案，已经针对新建隧道以不同方式穿越既有隧道的工况进行了室内模型试验，也得出了一些非常有意义的结论。而目前的研究基本都是采用常规室内模型试验的方法进行研究，尚未有离心模型试验的研究成果发表。A.M.Marshall(2009)［6］对新建隧道正交穿越既有管道的影响进行了离心模型试验研究，可以作为本课题研究的参考。Marshall采用离心模型试验对砂土中盾构隧道穿越既有管道进行了模拟，并使用先进的PIV技术结合传统的传感器对模型变形进行量测，得出了一个修正的高斯公式来计算砂土中盾构引起的地面变形。其试验采用排液来模拟地层损失，可以精确控制地层损失率。但是在这所有的试验及研究中无一例外地都没有考虑隧道开挖卸载和注浆的影响。

虽然一般的室内模型试验比离心模型试验操作简单，且更容易接近实际施工过程，但是不能真实地再现现场的应力水平。离心模型试验则能真实地再现现场的应力水平，又可以通过设计多组工况对施工参数进行分离研究，并能大大缩短研究时间。因此，利用离心模型试验结合数值分析对这一课题进行深入的研究是非常有利、非常必要的。本文参考已有的研究成果，采取离心模型试验的方法对新建盾构隧道近距离下穿越施工对既有隧道的影响这一课题进行研究，并在此基础上提出盾构近距离施工控制措施。

2 试验设计

2.1 试验设备

试验在同济大学岩土工程实验室TLJ-150型土工离心机上完成。该离心机最大容量为150 g-t，最大加速度为200 g，有效旋转半径为3.0 m。使用模型箱的有效尺寸为0.9 m×0.7 m×0.7 m(长×宽×高)。

2.2 离心模型试验原理

离心模型试验能利用高速旋转的离心机，在模型上施加超过重力N倍的离心惯性力，补偿模型因缩尺l/N所造成的自重应力的损失，使模型与原型应力、应变相等，变形相似(1/N)，破坏机理相同［7］。它比通常在静力(重力加速度)条件下的物理模型更接近于实际，因此它对模拟以自重为主要荷载的岩土结构物性状的研究就显得特别有效。目前离心模型试验在隧道及地下工程的研究中已经得到广泛应用。

利用相似原理可以得到模型和原型各物理量的相似准则，Taylor(1995)［8］给出了土工问题中常见参数的比例关系的推导过程。其中，土体固结问题的时间比例关系为N2，即模型试验中1 h对应于现场的N2h。这就是用离心模型试验模拟隧道的长期沉降的理论依据。

2.3 隧道开挖方案设计

本课题旨在研究新建隧道对既有隧道的影响。根据现场实测数据分析(邵华，张子新，2004;陈亮，黄宏伟［9］，2006;胡群芳，黄宏伟，2006)，新建隧道在到达既有隧道之前，由于推进面对土体的挤压，会使前方土体发生变形，从而引起既有隧道的变形，但这种影响不大，既有隧道的变形量不会超过1mm。因此，新建隧道对既有隧道的主要影响因素为开挖卸载、地层损失，以及壁后注浆。据此，选取排液法进行隧道开挖的模拟。本次试验在不停机状态下模拟隧道开挖卸载、地层损失和注浆过程。模型示意图如图1所示。

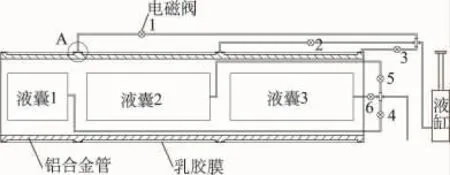
图1 试验模型示意图Fig.1 Schematic plot of the model

试验方法是在隧道模型外部套上3段乳胶膜，乳胶膜端部密封好，通过隧道模型上预留的接口与外界电磁阀相连，从而使乳胶膜与外界相连通。试验前在乳胶膜与隧道模型的空隙中注满重溶液，试验时通过电磁阀控制3个乳胶膜依次排出一定量的溶液来模拟施工时的地层损失。排液完成后通过液缸向3段乳胶膜中依次注入一定量的重溶液来模拟施工时的注浆过程。

具体的试验过程为首先控制乳胶膜1排液，完成第1段开挖，经过设计时间后往乳胶膜1中注液，完成第1段的注浆。此时第1段隧道的施工过程模拟完成。然后控制乳胶膜2排液，完成第2段开挖，经过设计时间后往乳胶膜2中注液，完成第2段注浆。此时，第2段隧道的施工过程模拟完成。最后控制乳胶膜3排液，完成第3段开挖，经过设计时间后往乳胶膜3中注浆。至此，第3段隧道的施工过程模拟完成。3段的地层损失率相同，均为1%。注浆率分别为120%，120%和200%。整个施工过程模拟完成后继续试验9.5h，模拟工后10.8 a的时间里新建隧道和土体的变形特征。

2.4 模型制备

由于真实的隧道是用管片和螺栓拼接起来的，所以要想在离心模型试验中完全真实地模拟隧道模型是不可能的。按照志波由纪夫提出的纵向等效连续化模型，令模型的纵向抗弯刚度EmIm与原型隧道的纵向抗弯刚度EpIp等效，即EI的相似性可表示为

这里，I表示管道的截面惯性矩。当管道壁厚与直径之比t/d比较小时，截面惯性矩可近似为I=πd3t/8。因此，EI的相似性要求为

因为直径的相似比dp/dm为N，由此可得，抗弯刚度EI的相似性为

试验采用铝合金空心管模拟隧道结构，试验中相似比N=100，根据等效刚度原理，可得出试验结构材料特性如表1所示。需要注意的是，在进行模型隧道设计时，使用的材料为均质铝合金圆筒。而实际工程中的隧道存在纵向和环向的接缝。因此，模型试验得出的隧道模型的内力会比实际工程中的隧道的内力要大，其纵向变形要比实际隧道更均匀。

表1给出了最终计算得到的模型尺寸。模型布置如图2所示。本次试验共有3层土，自上而下分别是④层土、⑤1层土、黄砂。具体参数见表2。其中，黄砂作为下部排水通道。

表1 原型与模型隧道参数Table 1 Parameters of the prototype and the model tunnel

2.5 数据采集

试验中，测量数据包括既有隧道的位移、应变和周围的孔隙水压力，新建隧道的性质没有考虑。

新建隧道下穿越既有隧道时，传感器的布置如图3所示。隧道A和隧道B每条隧道布置3个位移计，2个孔压计，10组半桥应变片。半结构隧道只在拱腰处布置1个孔隙水压力计。

图2 试验模型布置图Fig.2 Layout of the model

图3 既有隧道传感器布置图Fig.3 Layout of strain gauges in the existing tunnel

3 试验结果及分析

3.1 施工期既有隧道的沉降

新建隧道对第1条整结构隧道(B隧道)的位移影响和对第2条整结构隧道(A隧道)的位移影响如图4所示。试验中，A隧道左端位移计发生故障，数据未能采集。图中，曲线向下代表隧道沉降，曲线向上代表隧道隆起。

从图4可以看出，隧道位移的变化在排液或注浆后一段时间内才发生，说明土体的变形滞后于土体上荷载的变化。最终2条隧道均是中部位移大于端部位移2mm左右，说明隧道产生了纵向弯曲变形。前2段施工过程中，2条既有隧道的变化均较小，第1段地层损失时，B隧道中部沉降了0.3mm，A隧道中部沉降了0.2mm。第1段注浆时，B隧道中部隆起了1.3mm，A隧道中部隆起了0.4mm。第2段地层损失时，B隧道中部沉降了1mm，A隧道中部沉降了0.3mm。第2段注浆时，B隧道中部隆起了1.5mm，A隧道中部隆起了0.56mm。随着施工的推进，既有隧道的变形逐渐变大。第3段地层损失时，B隧道中部沉降了0.7mm，A隧道中部沉降了0.3mm。第3段注浆时，2条既有隧道均有显著的隆起，其中B隧道中部的隆起量为3.4mm，A隧道中部的隆起量为2.3mm。由此可见，在施工过程中注浆率越大，隧道隆起量也越大［10］。试验结束时A隧道底部距离新建隧道顶部距离为2cm，相当于实际工程中间距2 m。B隧道底部距离新建隧道顶部距离只有1cm，相当于实际工程中间距为1 m。可以看出，隧道间距也是影响既有隧道沉降的一个重要因素。

图4 施工期既有隧道沉降曲线Fig.4 Settlement curves of existing tunnels during the construction

3.2 工后既有隧道的沉降

施工完成后，离心机持续运行了9.5 h，模拟了工后10.8 a时间内隧道位移的变化。工后既有隧道的位移变化如图5所示。从图中可以看出，新建隧道在施工过程中既有隧道会向上隆起，而在施工结束后既有隧道会逐渐沉降。10a后A隧道的沉降取曲线中部的值，即16mm，同样B隧道的沉降取18mm。最终A，B两隧道的沉降量基本相同。上一节中指出，试验结束时A隧道底部距离新建隧道顶部距离为2cm，相当于实际工程中间距2 m。B隧道底部距离新建隧道顶部距离只有1cm，相当于实际工程中间距为1 m。从这里看出，如果B隧道与既有隧道的间距与A隧道间距相同，则工后B隧道的沉降量应该小于A隧道。即施工期注浆率越大，对周围地层的影响越大，既有隧道的后期沉降会越大。并且工后10 a内，既有隧道一直在沉降，试验结束时尚未收敛。这表明，施工的影响会持续相当长的时间。

图5 工后既有隧道沉降曲线Fig.5 Settlement curves of existing tunnels after the construction

3.3 施工期既有隧道纵向变形

根据施工过程中A，B两条既有隧道不同测点位移的变化，对其纵向变形进行分析。其中A隧道左端位移计出现故障，未采集到数据。根据A隧道上表面的应变观测数据(如图6所示)，可以看出A隧道上表面应变基本对称，因此可认为A隧道左端位移等于右端位移。A，B两隧道的纵向变形曲线如图7所示。从图中可以看出新建隧道的施工会引起既有隧道的不均匀沉降，既有隧道中部变形大于两端。A隧道的纵向最大差异沉降值为2mm，B隧道为5mm。

图6 A隧道上表面应变变化曲线Fig.6 Curves of strain of the upper surface of tunnel A

3.4 工后既有隧道的纵向变形

根据施工过程中A，B两条既有隧道不同测点位移的变化，对其纵向变形进行分析。A，B隧道的纵向变形曲线如图8所示。从图中可以看出，隧道的沉降速率逐年减小，说明隧道沉降在逐渐稳定。工后B隧道发生了倾斜，左端沉降比右端沉降大2.5cm左右。10a后A隧道的纵向最大差异沉降值为9mm。从图8中看出，A隧道的纵向差异沉降已基本达到稳定，后期变化很小。后期的变化主要是隧道整体的沉降。

图7 施工期既有隧道纵向变形曲线Fig.7 Longitudinal deformation of existing tunnels during the construction

图8 工后既有隧道纵向变形曲线Fig.8 Longitudinal deformation of existing tunnels after the construction

4 结论与展望

本文采用离心模型试验，对盾构下穿越对既有隧道及周围地层的影响进了研究，得出以下一些结论:

(1)隧道位移的变化在排液或注浆后一段时间内才发生，说明土体的变形滞后于土体上荷载的变化。最终2条既有隧道均是中部位移大于端部位移2mm左右，说明隧道产生了纵向弯曲变形。

(2)新建隧道施工过程中既有隧道会向上隆起，在施工结束后会逐渐沉降。

(3)地层损失率相同，当注浆率较小时，既有隧道的位移变化较小，随着施工的推进，既有隧道的变形逐渐变大。施工期注浆率越大，对周围地层的影响越大，既有隧道的后期沉降会越大。隧道间距也是影响隧道沉降的重要因素。

(4)新建隧道的地层损失会引起既有隧道的沉降，而新建隧道注浆会引起既有隧道隆起。新建隧道的施工会引起既有隧道的不均匀沉降，既有隧道中部变形大于两端变形。

本次试验对新建盾构隧道近距离下穿越既有隧道的影响进行了研究，取得了一些初步结论。但是盾构穿越课题系统性很强、很复杂，由于条件所限，本工作仍有较多不完善之处，后期应对盾构施工引起既有隧道变形的其他因素进行离心模型试验的研究。因而，后续研究中不仅需要进行多组对比性试验，以期得出定量的结论;还需要对盾构施工引起既有隧道的变形理论进行深入研究。现有的弹性地基梁理论无法反映隧道三维变形的缺陷，因此，研究盾构隧道-土-既有隧道三维共同作用对于认清盾构近距离施工的机理具有重要的意义。

［1］志波由纪夫，川岛一彦，大日方尚己.ツ-ルドトネルの耐震解析にる长手方向覆工刚性の评价法［J］.日本土木学会论文集，1988:319－327.

［2］KIM SH.Model Testing and Analysis of Interactions Between Tunnels in Clay［D］.UK:University of Oxford，1996.

［3］周文波，吴惠明.上海地铁二号线盾构法隧道施工难题浅述［J］.上海市政工程，2000，(3):68－77.(ZHOU Wen-bo，WU Hui-ming.Challenges in Shield Tunnel Construction of Shanghai Metro Line 2［J］.Shanghai Municipal Engineering，2000，(3):68－77.(in Chinese))

［4］俞 涛.地铁盾构隧道近接施工影响的数值模拟及模型试验研究［D］.成都:西南交通大学，2005.(YU Tao.Numerical Simulation and Model Test for Effects of Close-Spaced Construction of Subway Shield Tunnels［D］.Chengdu:Southwest Jiaotong University，2005.(in Chinese))

［5］何 川，苏宗贤，曾东洋.地铁盾构隧道重叠下穿施工对上方已建隧道的影响［J］.土木工程学报，2008，41(3):91－98.(HE Chuan，SU Zong-xian，ZENG Dong-yang.Influence of Metro Shield Tunneling on Existing Tunnel Directly Above［J］.China Civil Engineering Journal，2008，41(3):91－98.(in Chinese))

［6］MARSHALL A M.Tunneling in Sand and Its Effect on Pipelines and Piles［D］.London:University of Cambridge，2009.

［7］KIMURA T，KUSAKABE O.Centrifuge Model Tests 2:Introduction［J］.Soils and Foundations，1987，35(11):68－74.

［8］TAYLOR R N.Geotechnical Centrifuge Technology［M］.London:Blackie Academic ＆ Professional，1995:20－33.

［9］陈 亮，黄宏伟，王如路.近距离上部穿越对原有隧道沉降的影响分析［J］.土木工程学报，2006，39(6):83－87.(CHEN Liang，HUANG Hong-wei，WANG Rulu.Analysis of the Observed Longitudinal Settlement of a Tunnel Caused by an Adjacent Shield Tunneling on Top［J］.China Civil Engineering Journal，2006，39(6):83－87.(in Chinese))

［10］叶 飞，朱合华，丁文其，等.施工期盾构隧道上浮机理与控制对策分析［J］.同济大学学报，2008，36(6):738－743.(YE Fei，ZHU He-hua，DING Wen-qi，et al.Analysis and Control of Upward Moving of Shield Tunnel Under Construction［J］.Journal of Tongji University(Natural Science)，2008，36(6):738－743.(in Chinese ))