三峡水库运用初期库区水沙输移数值模拟
黄仁勇,李 飞,张细兵
(1.长江科学院河流研究所,武汉 430010;2.长江水利委员会规划计划局,武汉 430010)
1 研究背景
泥沙问题是三峡工程中的关键技术问题之一。在三峡工程泥沙问题研究过程中,我国主要采取原型观测分析与调查、数学模型计算和实体模型试验相结合的研究方法,取得了许多研究成果,也推动了整个泥沙学科的发展。同时,泥沙数学模型也在广泛应用中不断取得新的进展,其中长江科学院和中国水利水电科学研究院以一维不平衡输沙理论为基础建立的三峡水库一维水沙数学模型,已成为目前比较成熟的数学模型,并在三峡工程泥沙研究中起到了基础和关键性作用[1]。
三峡水库库长700余km,区间支流众多,各支流的入库水量和库容也较大,为提高水库调蓄计算的精度,有必要将更多支流纳入计算范围;而以往研究均没有进行库区小支流的水沙输移计算,对区间支流库容及来水影响考虑不够。本文考虑水沙输移过程中的非恒定性,建立了三峡水库一维非恒定水沙数学模型,该模型为一树状河网模型,可以将更多支流纳入水沙输移计算范围。
自2003年6月三峡水库投入运用以来,三峡库区的冲淤特点发生了明显变化,库区河道由整体上的冲淤基本平衡转向持续淤积状态,为准确了解三峡库区水流及河床在水库运行后的变化规律,长江水利委员会水文局对三峡水库蓄水后水沙资料进行了详细观测,这为数学模型验证与改进提供了宝贵的资料。本次验证选用三峡水库运用后2003年6月至2009年12月实测水沙资料,检验模型对库区洪水演进过程、沿程水位变化过程及河床冲淤演变过程的模拟精度,分析模型预测计算结果的可信度,为今后模型的改进与应用提供新的依据。
2 数学模型的建立
三峡库区支流众多,建立三峡水库一维非恒定水沙数学模型应同时考虑干支流水沙运动,将水库干支流河道分别视为单一河道,河道汇流点称为汊点,则水沙数学模型应包括单一河道水沙运动方程、汊点连接方程和边界条件3部分[2]。
2.1 单一河道水沙运动方程
(1)模型选用的描述单一河道水流与泥沙运动的基本方程为[3]:
水流连续方程


水流运动方程
泥沙连续方程

河床变形方程

式中:ω为泥沙沉速;角标i为断面号;Q为流量;A为过水面积;t为时间;x为沿流程坐标;Z为水位;K为断面流量模数;S为含沙量;S*为水流挟沙力;ρ'为淤积物干密度;B为断面宽度;g为重力加速度;α为恢复饱和系数;Ad为河床冲淤面积。
2.2 汊点连接方程
2.2.1 流量衔接条件
进出每一汊点的流量必须与该汊点内实际水量的增减率相平衡,即

式中Ω为汊点的蓄水量。如将该点概化为一个几何点,则Ω=0。
2.2.2 动力衔接条件
如果汊点可以概化为一个几何点,出入各个汊道的水流平缓,不存在水位突变的情况,则各汊道断面的水位应相等,即

2.3 边界条件
计算中不对某单一河道单独给边界条件,而是将纳入计算范围的三峡水库干支流河道作为一个整体给出边界条件,各干支流进口给流量和含沙量过程,模型出口给水位过程、流量过程或水位流量关系。
2.4 有关问题的处理
2.4.1 床沙交换及级配调整
关于床沙交换及级配调整,本模型采用3层模式,即把河床淤积物概化为表、中、底3层,表层为泥沙的交换层,中间层为过渡层,底层为泥沙冲刷极限层。规定在每一计算时段内,各层间的界面都固定不变,泥沙交换限制在表层内进行,中层和底层暂时不受影响。在时段末,根据床面的冲刷或淤积向下或向上输送表层和中层级配,但这2层的厚度不变,底层厚度随冲淤厚度的变化而变化。
2.4.2 水流挟沙力计算
水流挟沙力公式为[4]:

式中:S*为水流总挟沙力;u为平均流速;h为水深;ωm为非均匀沙平均沉速;pL为第L组泥沙的级配;ωL为第L组泥沙的沉速;k为挟沙力系数,水库为0.03,天然河道为0.02。
2.4.3 恢复饱和系数α
恢复饱和系数是泥沙数学模型计算的重要参数,是一个综合系数,需要由实测资料反求。但是影响因素很多,既与水流条件有关,又与泥沙条件有关,随时随地都在变化,在大多数泥沙冲淤计算中都假定为一正的常数,通过验证资料逐步调整。本模型对泥沙冲淤采用分粒径组算法,如果对各粒径组都取同样的α值,由于各组间的沉速相差可达几倍甚至几百倍,因而从计算结果看,在同一断面上小粒径组相对于大粒径组来说其冲淤量常常可忽略不计,这往往与实际不尽相符。从三峡水库蓄水运用以来进出库的各粒径组泥沙实测资料来看,各粒径组泥沙的沿程分选现象均非常突出。目前对恢复饱和系数α取值的研究非常多,基本上有如下共识:①不同粒径组泥沙的恢复饱和系数值不同;②恢复饱和系数取值应随泥沙粒径的增大而减小;③恢复饱和系数值应随空间和时间而变化。为此本模型在计算中对不同粒径组的恢复饱和系数αL采用如下经验公式计算:

2.4.4 节点分沙
进出节点各河段的泥沙分配,主要由各河段临近节点断面的边界条件决定,并受上游来沙条件的影响。本模型采用分沙比等于分流比的模式,即

3 数学模型求解
3.1 水流方程求解
可采用三级解法对水流方程进行求解,首先对水流方程(1)和(2)采用普列斯曼的四点隐式差分格式进行离散[5],可得差分方程如下:

式中系数均按实际条件推导得出。
假设某河段中有m个断面,将该河段中通过差分得到的微段方程(12)和(13)依次进行自相消元,再通过递推关系式将未知数集中到汊点处,即可得到该河段首尾断面的水位流量关系:

式中系数α1,β1,δ1,θm,ηm,γm由递推公式求解得出。
将边界条件和各河段首尾断面的水位流量关系带入汊点连接方程,就可以建立起以三峡水库干支流河道各汊点水位为未知量的代数方程组,求解此方程组得各汊点水位,逐步回代可得到河段端点流量以及各河段内部的水位流量。
3.2 泥沙方程求解
对泥沙连续方程(3)用显格式离散得

对河床变形方程(4)进行离散得

其中,Δt为时段;Δx为两断面间距。在求出干支流河道所有断面的水位流量后,即可根据式(16)自上而下依次推求各断面含沙量,汊点分沙计算采用分沙比等于分流比的模式,最后根据式(17)进行河床变形计算。
4 数学模型验证
4.1 计算条件
计算范围为干流朱沱-三峡坝址(见图1),长约760km。考虑嘉陵江、乌江、綦江、木洞河、大洪河、龙溪河、渠溪河、龙河、小江(支流小江又包含南河、东河、普里河、彭河等支流)、梅溪河、大宁河、沿渡河、清港河、香溪河共14条支流。起始计算地形中朱沱-李渡为1996年实测地形,李渡-三峡坝址为2003年蓄水前实测地形。计算进口采用干流朱沱站、嘉陵江北碚站、乌江武隆站3站2003年6月1日至2009年12月31日逐日平均流量和含沙量。出口采用庙河站相应时段逐日平均水位。区间来流量在计算河段内分配到入汇支流上,没有考虑区间来沙。
4.2 水位及流量验证
根据现有实测资料,选用沿程各主要水文站的2003-2004年实测水位流量过程与模型的计算结果进行了比较,结果见图2和图3,表1为三峡水库2004年库区部分测站最高洪水位值验证结果。由图表可见,模型计算的沿程各水文站洪水演进传播过程及水位变化过程与实测情况基本一致,最高洪峰水位的出现计算值与实测值几乎同步,模型验证结果与实测值符合较好。

表1 2004年三峡库区部分测站最高洪水位验证Table 1 Verification of the highest flood level at stations in the TGR area in 2004
4.3 干流水文站输沙量验证

图1 三峡水库库区干支流示意图Fig.1 Schematic diagram of the mainstream and tributaries in the TGR area
图4为三峡库区部分主要水文站2003-2004年含沙量过程验证结果,各站计算结果与实测值基本一致,但计算含沙量峰值比实测值小,而中小流量时计算值又稍有偏大,由于多数时期计算值与实测值相近,互有大小,所以全年累积输沙量与实测值还是比较接近的(见表2)。

图2 部分测站水位过程验证Fig.2 Verification of water level history at three stations

图3 部分测站流量过程验证图Fig.3 Verification of water discharge history at three stations
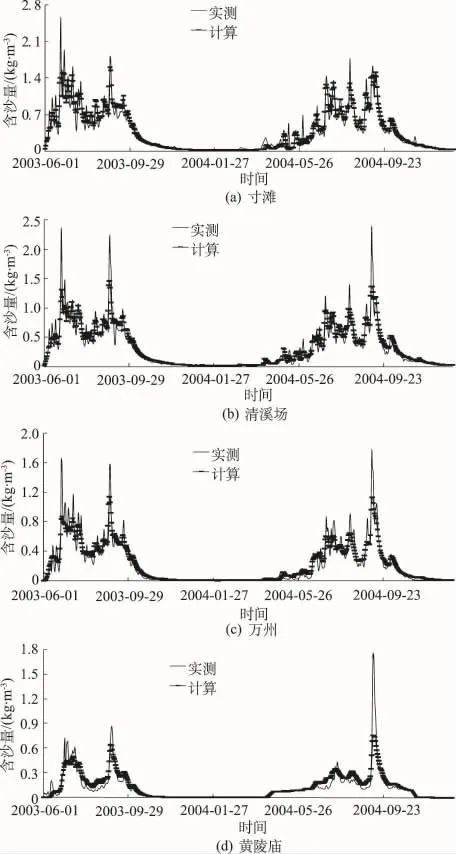
图4 部分测站含沙量过程验证Fig.4 Verification of sediment concentration history at four stations

表2 主要测站输沙量验证Table 2 Verification of sediment discharge of some major stations 亿t
4.4 淤积量及排沙比验证
表3和表4分别为三峡库区淤积量和排沙比验证结果,从淤积过程、淤积分布及排沙比计算结果看,模型计算值与实测值均吻合较好。以朱沱至坝址为库区淤积统计范围,按输沙量法统计,水库运用至2009年底,朱沱至清溪场段、清溪场至坝址段及全库区分别淤积1.392,9.773,11.18亿t,与相应实测值1.631,9.338,10.97亿t接近。从累积淤积量看,模型全库段累积淤积量计算值与实测值相对误差为1.9%。从排沙比验证结果看,模型累积排沙比计算值与实测值相差约1.4%,且对排沙比较大(如2005年)和较小(如2006年)的年份均取得了较为满意的验证效果。

表3 淤积量及分布计算结果Table 3 Calculated results of deposition volume and its distribution

表4 排沙比计算值与实测值对比Table 4 Comparison between the calculated results and observed data of discharged sediment ratio
5 结论
鉴于以往研究中的三峡水库水沙数学模型对库区支流影响考虑不够的现状,本文考虑水沙输移过程中的非恒定性及库区更多支流库容的影响,基于三级解法的基本思想,建立了三峡水库一维非恒定水沙数学模型,提高了水沙计算精度;采用三峡水库蓄水运用后2003-2009年实测资料对模型进行了验证,计算的水位流量过程、输沙量及排沙比等与实测值符合较好。验证结果表明,此模型在非恒定输沙计算方面有较好的精度,模型对三峡水库水沙输移及泥沙冲淤模拟计算基本合适,该模型可为三峡水库冲淤预测和优化调度研究提供技术支持。
[1]彭 杨,张红武.三峡库区非恒定一维水沙数值模拟[J].水动力学研究与进展,2006,21(3):285-292.(PENG Yang,ZHANG Hong-wu.1-D Numerical Simulation of Unsteady Flow and Sedimentation Transport at the Three Gorges Reservoir(TGR)[J].Journal of Hydrodynamics,2006,21(3):285-292.(in Chinese))
[2]黄仁勇,黄 悦.三峡水库干支流河道一维非恒定水沙数学模型初步研究[J].长江科学院院报,2009,26(2):9-13.(HUANGRen-yong,HUANGYue.Preliminary Study on 1-D Numerical Simulation of Unsteady Flow and Sediment Transport in Mainstream and Tributaries of Three Gorges Reservoir Area[J].Journal of Yangtze River Scientific Research Institute,2009,26(2):9-13.(in Chinese))
[3]谢鉴衡.河流模拟[M].北京:中国水利水电出版社,1988:111-116.(XIE Jian-heng.River Simulation[M].Beijing:China Water Power Press,1988:111-116.(in Chinese))
[4]张瑞瑾.河流泥沙动力学[M].北京:中国水利水电出版社,1998:181-190.(ZHANG Rui-jin.River Sediment Dynamics[M].Beijing:China Water Power Press,1998:181-190.(in Chinese))
[5]董耀华,黄煜龄.天然河道长河段一维非恒定流数模研究[J].长江科学院院报,1994,11(2):10-17.(DONG Yao-hua,HUANG Yu-ling. A Mathematical Model of One-Dimensional Unsteady Flow in Long-Distance Natural Channel[J].Journal of Yangtze River Scientific Research Institute,1994,11(2):10-17.(in Chinese ))

