小波分析法实现水轮发电机轴心轨迹的提纯
伍卫平,倪国胜,范钦红,李东风,曹树林
(1.水利部 水工金属结构质量检验测试中心,郑州 450044;2.郑州辰维科技股份有限公司,郑州 450001)
水轮发电机轴心轨迹是转子振动信号的重要图形征兆,包含大量的故障信息;分析轴心轨迹是诊断水轮机机组振动故障的重要方法[1]。
工程实际中得到的轴心轨迹一般都会受到噪声的污染,不易提取轴心轨迹的准确及可靠特征。为了得到清晰的轴心轨迹,需要对获得的轴心轨迹进行降噪提纯处理[2]。
传统傅立叶变换存在不能用于非平稳信号、不能同时进行时-频局部化分析(所谓时-频局部化分析就是指同时兼顾时间分辨率与频率分辨率,能根据需要对信号局部进行分析的方法)的缺陷;小波分析法[3]克服了传统傅立叶变换的缺陷,它是一种对信号同时进行时频分析的手段,具有多分辨率的特点,可以很好地用于非平稳信号的分析。利用小波阈值去噪法可以方便地从混有强噪声的信号中提取原始信号[4-5],能够较好地获得清晰的水轮发电机轴心轨迹;而谐波小波[6]的提纯效果更好,且其具有函数表达式明确、算法实现简单、保持数据点数与采样频率不变等诸多优点。
1 水轮机组轴心轨迹特点及模拟仿真
1.1 水轮机组振动的危害、产生机理及轴心轨迹特点
水轮机组的振动会使设备或结构承受过大的交变载荷,成为疲劳破坏的重要原因。强烈的振动将影响水轮机组的正常运行,并降低机组和一些零部件的使用寿命。
一般来说,水轮发电机组的振动是机械、水力、电气等因素相互耦合作用的结果,振动的机理很复杂。
水轮发电机组的轴心轨迹是指机组主轴轴心上一点相对于轴承座运动而形成的轨迹。
由于轴心轨迹中蕴含着大量的故障信息,因此采用轴心轨迹形状来判断机组的运行状态或故障是非常有效的。
常见振动故障的机理与信号特征如表1所示[2]。

表1 常见振动故障的机理与信号特征Table 1 Common vibration faults and signal characteristics
实际故障诊断中得到的轴心轨迹一般都会受到噪声的污染,原始轴心轨迹会变得比较杂乱,为了得到清晰的轴心轨迹,需要对获取的原始轴心轨迹进行降噪提纯处理。
1.2 轴心轨迹的仿真模拟
含有噪声的轴心轨迹的仿真方程为


图1 轴心轨迹图Fig.1 Sketch of the shaft orbit

式中:Ai为各个频段的振幅;ω为振动的基频;n为倍频数;φi为初相位;Ft,Fs为干扰信号。
首先,通常情况下,构造如式(2)所示的方程来仿真各种轴心轨迹的形状:

式中:A1,A2,α1,α2分别为x(t)的一倍频、二倍频分量的幅值与初相位;B1,B2,β1,β2分别为y(t)的一倍频、二倍频分量的幅值与初相位。
通过改变 A1,A2,α1,α2,B1,B2,β1,β2这 8个参数值的大小,基本上可以获得各种常见的轴心轨迹形状,加入高频噪声,就可以得到仿真所需要的各种含有噪声的轴心轨迹,如图2所示。
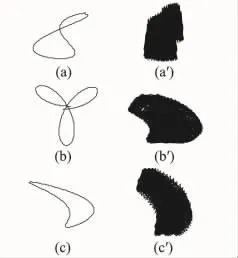
图2 含高频噪声的模拟轴心轨迹图Fig.2 Simulated shaft orbit with high frequency noise
2 小波阈值去噪的原理
小波具有局部非零、波形衰减、能同时进行时频分析的特点。
二进小波变换具有分辨率随分解尺度j成2j的增加、频谱窗口变宽、能够不断细化的优良特性。
以一维信号的去噪处理为例,来阐述一下小波去噪的基本原理。基本的含噪模型表示为

式中:s(i)是含噪信号;f(i)是有用信号;e(i)是噪声信号;ε是噪声强度。对信号s(i)去噪的目的是要抑制信号中的噪声部分,从而在s(i)中恢复出真实信号f(i)。
对某一含噪信号进行小波分解,如果进行3层分解,其分解过程如图3所示。通常情况下,有用信号包含在低频的表示近似信息的a1,a2和a3中,噪声部分包含在高频的表示细节信息的d1,d2和d3中。
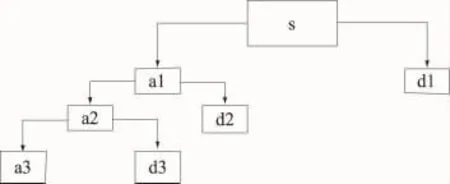
图3 小波分解示意图Fig.3 Schematic diagram of wavelet decomposition
一般来说,小波用于信号阈值去噪的基本步骤主要包括如下3步[7]:
(1)选择合适的小波基函数对信号进行小波分解;
(2)选择合适的阈值函数及合适的阈值对小波分解高频系数进行阈值化处理(可以使用全阈值或者尺度分解时各层采用不同的阈值);
(3)使用小波分解的低频系数及阈值化处理后的高频系数进行小波逆变换得到估计信号(即原始信号的估计值)。
采用小波阈值去噪时,关键是阈值函数的选择和阈值的估计;传统的阈值去噪方法有硬阈值法和软阈值法。
假设含噪生信号的小波分解系数为ωj,k,取阈值为T;则硬阈值、软阈值处理后的小波系数ω'j,k分别用式(4)、(5)表示。传统的阈值[6]常取值为T=,其中N表示小波系数的长度,σ表示小波系数的标准差。硬阈值函数:

软阈值函数:

硬阈值函数是不连续的;软阈值函数虽然连续,但是小波系数阈值化处理后与分解值存在固定的偏差,在一定程度上会引起重构信号的失真。并且这2种方法没有考虑到阈值的自适应性。
改进的软阈值函数[8]为

上述改进的阈值函数是连续的,并且克服了传统软阈值法中小波系数阈值化处理后与分解值存在固定偏差的弊端;大的小波分解系数的保留误差将比小的小波系数的保留误差小得多。以上3种阈值函数所对应的曲线如图4所示。同的阈值其中N表示对应的尺度j下小波分解系数向量的长度。

图4 阈值函数曲线Fig.4 Threshold functions curves
3 谐波小波分析法
虽然小波对于处理非平稳信号是非常有效的,但通常的小波算法[9](如 Mallat算法)在分解信号时要隔二抽一,随着分解层数的增加,就会使小波分解各层的数据点数和采样频率减半。由于数据点数较少,信号细节有可能存在着失真;并且小波基函数及分解尺度的选择很麻烦。
而谐波小波[10]具有明确的函数表达式,无需经过繁冗的尺度函数迭代;其分解算法是通过信号的快速傅里叶变换与快速傅里叶逆变换实现的,算法简单。其伸缩与平移构成了L2(R)空间的规范正交基。谐波小波滤波算法不仅能使不同频段信号分离开来,而且能保持各段数据点数不变、采样频率不变。
我们采用下面的表达式来定义谐波小波,
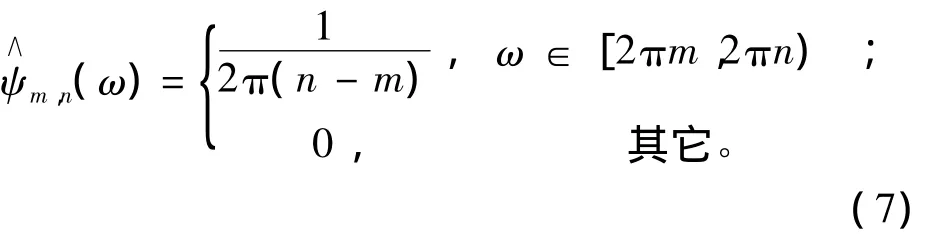
式中:m,n决定谐波小波的变换尺度j,且有 n=2m=2j,当m=0 时,n=1。
在j=0时,谐波小波的傅里叶变换频带位于[2π,4π],而在第j层,其频谱位于[(2j+1)π,(2j+2)π]。随着j的增大,其频谱带宽以二进制的方式逐渐变宽,但幅值降低,如图5所示。

图5 不同层谐波小波的频谱Fig.5 Frequency spectrum of harmonic wavelet at different levels
根据小波变换的定义,相对于尺度为j的谐波小波ψm,n(t),信号f(t)的小波变换可以表示为

根据傅里叶变换的性质,则有
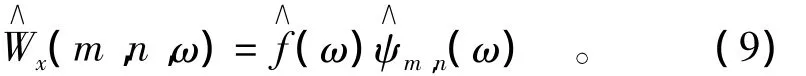

图6 尺度j下的信号谐波小波变换Fig.6 Signal harmonic wavelet transform at level j
由于谐波小波是一个理想的带通滤波器,可以将任何信号f(t)∈L2(R)正交、无冗余、无遗露地分解到相互独立的频段上。各个频段之间是相互正交的,方便研究某一特定频段的成分。因此,可以很好地将其应用于水轮机发电机轴心轨迹的去噪提纯中。
4 仿真模拟实验及分析比较
计算机模拟的外“8”字形原轴心轨迹图和含噪轴心轨迹图如图7所示。采用db4小波基函数分别将横轴信号x和纵轴信号y进行三尺度分解,得到对应的各层近似和细节信息,如图8所示;从图8中可以分析看出,噪声部分主要包含在表示细节信息的d1,d2和d3中。

图7 外“8”字形轴心轨迹图Fig.7 Shaft orbits of“8”shape

图8 含噪信号及其各层近似、细节信息Fig.8 Noisy signals,approximations and the details at each level
分别采用小波硬阈值法、小波软阈值法、改进的小波软阈值法、谐波小波法4种方法来提纯轴心轨迹,前3种方法均采用db4小波基函数;提纯结果如图9所示。
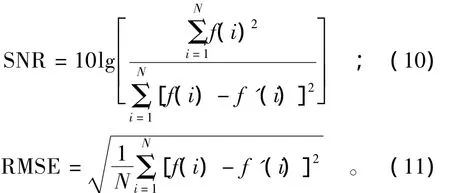
从图9的提纯结果来分析,对于小波阈值去噪,传统硬阈值法中会丢失一些有用的信息,传统软阈值去噪中,在一定程度上会引起重构信号的失真;如何合理地给定阈值直接影响着去噪的效果,不容易把握;实际上小波基函数的选择、小波分解的尺度也影响小波阈值去噪的效果。如果每个尺度上的阈值选择更为合理些,改进的小波软阈值去噪法效果会更好。而小波谐波法提纯效果更佳,且去噪算法实现更简单。
从表2中的数据可以分析得出:小波谐波法处理后信号的信噪比最高,均方根误差最小,其次是改进的软阈值法、软阈值法、硬阈值法。

表2 4种轴心轨迹提纯方法的比较Table 2 Comparison of shaft orbit identification of the 4 methods
5 结论
本文采用计算机模拟仿真,在传统小波硬、软阈值去噪法基础上提出一种新的软阈值去噪法和谐波小波去噪法,用于提纯水轮发电机轴心轨迹,得到了清晰的轨迹图,对于水轮机组振动故障诊断有很好的指导性。对于改进的小波软阈值去噪法,性能比传统小波阈值去噪法有了较大的改进,关键之处在于阈值的选取,但阈值函数的构造及阈值的选择比较麻烦,具有一定的主观性和不确定性;引入的小波谐波法程序实现更为简单,效率更高,是一种更为理想的信号去噪、轴心轨迹提纯的方法。
[1]夏松波,张嘉钟,徐世昌,等.旋转机械故障诊断技术的现状与展望[J].振动与冲击,1997,16(2):1-6.(XIA Song-bo,ZHANGJia-zhong,XU Shi-chang,et al.Present Situation and Prospect about Fault Diagnosis Technology of Rotating Machines[J].Chinese Journal of Vibration and Shock,1997,16(2):1-6.(in Chinese))
[2]倪传坤.水轮机组轴心轨迹自动辨识研究与实现[D].武汉:华中科技大学,2004.(NI Chuan-kun.Research on Auto-identification of Shaft Orbits for Hydro-generator Sets and Its Application[D].Wuhan:Huazhong University of Science& Technology,2004.(in Chinese))
[3]樊启斌.小波分析[M].武汉:武汉大学出版社,2008.(FAN Qi-bin.Wavelet Analysis[M].Wuhan:Wuhan University Press,2008.(in Chinese))
[4]马宏伟,王 彬.小波变换在超声检测信号去噪中的应用[J].无损检测,2004,26(2):68-71.(MA Hong-wei,WANG Bin.Application of Wavelet Transform to Signal Denoising in Ultrasonic Testing[J].Chinese Journal of Nondestructive Testing,2004,26(2):68-71.(in Chinese))
[5]刘镇清,黄蕾菊.小波变换及其应用[J].无损检测,2001,23(4):174-177.(LIU Zhen-qing,HUANG Leiju.Wavelet Transform and Its Application[J].Chinese Journal of Nondestructive Testing,2001,23(4):174-177.(in Chinese))
[6]DONOHO D L.De-noising by Soft-Thresholding[J].IEEE Transactions on Information Theory,1995,41(3):613-627.
[7]周 伟.MATLAB小波分析高级技术[M].西安:西安电子科技大学出版社,2006.(ZHOU Wei.Advanced Technology of Wavelet Analysis Based on MATLAB[M].Xi’an:Xidian University Press,2006.(in Chinese))
[8]陈晓楠,索继东,柳晓鸣.基于改进小波阈值函数的船用雷达回拨去噪[J].沈阳工业大学学报,2010,32(2):196-199.(CHEN Xiao-nan,SUOJi-dong,LIU Xiao-ming.Echo Denoising of Shipborne Radar Based on Improved Wavelet Threshold Function[J].Chinese Journal of Shenyang University of Technology,2010,32(2):196-199.(in Chinese))
[9]MALLAT S,HWANG W L.Singularity Detection and Processing with Wavelets[J].IEEE Transactions on Information Theory,1992,38(2):617-643.
[10]李舜酩,吕国志,许庆余.转子轴心轨迹的谐波小波提纯[J].西北工业大学学报,2001,19(2):221-224.(LI Shun-ming,LV Guo-zhi,XU Qing-yu.On Obtaining Accurate Rotor Sub-frequency Signal with Harmonic Wavelet[J].Chinese Journal of Northwestern Polytechnical University,2001,19(2):221-224.(in Chinese))

