滚动体具有局部缺陷滚动轴承的动力学分析

东亚斌，廖明夫，高 琦

(1．西北工业大学动力与能源学院，陕西 西安 710072;2．中国重型机械研究院有限公司，陕西 西安 710032)

0 前言

滚动轴承的动力学行为对整个转子系统的动力学行为有着很大的影响，特别是当其产生故障时，将诱发整个系统产生故障。因此研究故障轴承的动力学行为，对尽早发现轴承故障，保证设备正常运转具有十分重要的意义。

当滚动体具有点蚀缺陷时，在径向载荷作用下，缺陷滚过内外圈，接触副由于释放变形将使轴承产生冲击振动。同时由于滚动体的位置随保持架的旋转而周期性变化，因此冲击振动信号被保持架的旋转信号调制，轴承的振动信号频率成分除了滚动体的自转频率外，应该还包括保持架的旋转频率以及信号调制形成的边频。文献［1］所建立的滚动体故障模型虽然能够模拟出滚动体的自转频率，但是没有模拟出边频成分。文献［2-3］所建模型不是严格意义上的动力学模型。文献［4-6］所建模型虽然将上述频率都模拟出来，但是将接触副释放的变形量当作缺陷的深度，这显然不完全符合实际情况。

1 滚动体具有单一点蚀故障的滚动轴承的建模

建立如图1所示的滚动体具有单一局部故障滚动轴承的动力学模型。假设滚动轴承的保持架不动，即滚动体的位置角θj不变。

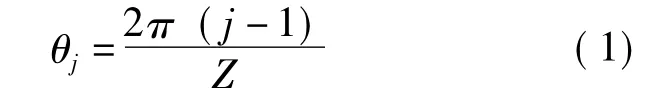
图1 滚动体具有单一局部故障滚动轴承的模型Fig.1 Model of rolling bearing with single local defect on rolling element

此时，内圈的角速度为ωs－ωc，方向不变。而外圈以角速度ωc沿与内圈旋转方向相反的方向旋转，如图1a所示。建立如图1所示的坐标系，坐标原点固定于保持架的中心点，两个坐标轴固结于保持加上。以与内圈旋转方向相反的方向为正。径向载荷作用于外圈上。设缺陷存在于第k个滚动体上，当其以角速度ωb自转到与内圈或外圈接触时，被挤压的套圈将会释放一定的变形，从而引起接触载荷的突变，激起轴承产生冲击振动。

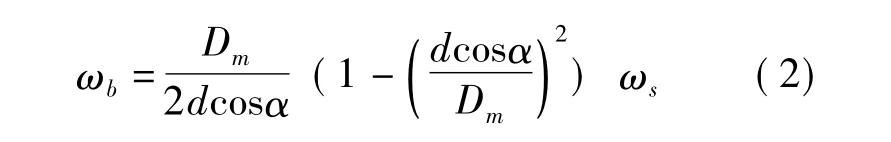
令第j个滚动体变形量为δbj，由于缺陷的存在，缺陷滚过内圈或外圈，接触副将会释放一定的变形，此时接触副的变形量可表示为

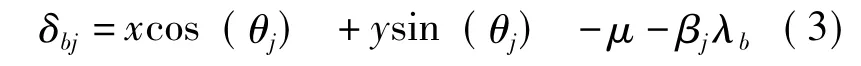
式中，θj由式 (1)计算;λb为第k个滚动体的缺陷滚过套圈时，套圈释放的变形量，可由如图1b所示的故障模型来计算。

在该模型中，缺陷被定义成截面为矩形的凹坑，其大小由沿圆弧切线方向的宽度b和深度Cd确定。滚动体缺陷滚过套圈时，接触变形的释放是由套圈向滚动体缺陷中释放。由于内外圈滚道直径不同，因此，对于同样大小的缺陷，其释放的变形不同。

由图1b所示的几何关系可得内圈释放的最大变形量为

式中，ri为内圈滚道半径。

外圈释放的最大变形量为

式中，ro为外圈滚道半径。

由此可定义λi为

对于缺陷和外圈接触的情况，式 (3)中的开关量βj为

对于缺陷和内圈接触的情况，βj为

式中，φdefect为缺陷的初始位置角，定义为滚动体缺陷与外圈接触点径向半径之间的夹角;Δφdefect为缺陷的跨度角，其计算值为

当缺陷和外圈接触的时，滚动体自转圈数nj，可表示为

由Hertz接触理论可知，在第k个滚动体处的接触载荷可表示为

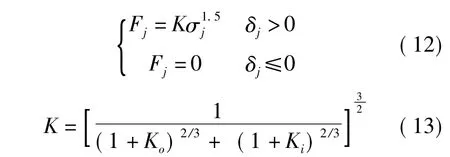
式中，K为等效接触变形系数;Ki、Ko分别为滚动体与内、外圈的接触变形系数，其计算方法参阅文献 ［8］。

将 (13)向X轴和Y轴投影，可得X方向和Y方向的分力为

X方向和Y方向作用于外圈的总的接触载荷为

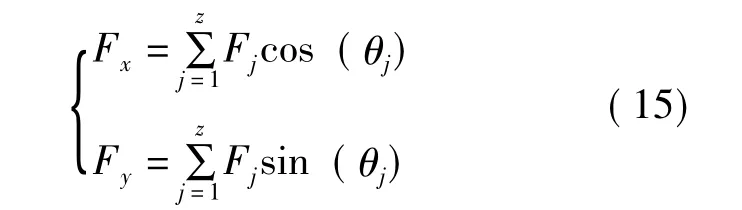
由于假定保持架不动，外圈以角速度ωc沿正方向旋转，因此，作用于外圈上的径向载荷Fr也以角速度ωc沿正方向旋转。由牛顿第二定律可得，滚动体具有单一局部故障滚动轴承外圈的二自由度振动方程为

式中，m为外圈的质量;C为等效阻尼。

2 数值仿真

根据轴承游隙的大小不同，滚动体缺陷与套圈的接触分为单边接触和双边接触两种情况。本文以6307型轴承双边接触形式为例进行，计算所定义的故障参数见表1。

表1 6307轴承的故障参数Table 1 Fault parameters of bearing 6307

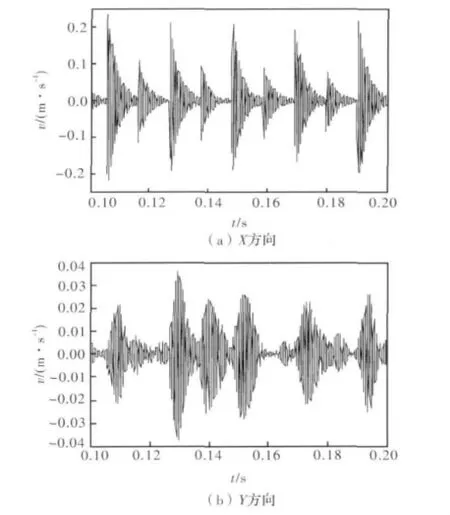
图2 滚动体具有单一局部故障滚动轴承的振动速度仿真信号Fig.2 Simulation signal of vibration velocity for rolling bearing with single local defect on rolling element

由图2可知，对于双边接触的情况，在0.1 s内有9个等间隔的波峰，相当于滚动体缺陷冲击的频率大概为90 Hz左右，由式 (17)计算得到双边接触情况下，滚动体缺陷的理论冲击频率为

因此，仿真信号波峰的重复频率基本上和滚动体缺陷的理论冲击频率相对应。另外，从图中还可以看出，冲击波峰的分布是大小尖峰成对出现的，大的代表缺陷与外圈接触，小的波峰代表缺陷与内圈接触。

从图3中可知，X、Y方向的振动位移信号和振动速度信号在低频段的频率成分主要包括:滚动体的公转旋转频率 (9.77 Hz)、滚动体双边冲击频率及其倍频 (94.6 Hz、189.2 Hz等)以及它们形成的边频 (84.8 Hz、104.3 Hz、179.4 Hz以及189.97 Hz等)。这恰好和实际进行滚动体故障双边接触诊断所用判据一致。

图3 滚动体具有单一局部故障滚动轴承的振动位移仿真信号的频谱Fig.3 Frequency spectrum of vibration displacement simulation signal for rolling bearing with single local defect on rolling element

3 实验验证

为了验证所建模型的有效性，本文采用6307型轴承。在其中一个滚动体上利用电蚀方法生成一个宽度为1.5 mm、深度为0.2 mm的划痕。安装在转子实验台上，并利用Brüel＆Kjaer 4381型压电式加速度传感器测取轴承支座振动信号。采样率为26 kHz，轴转速为1530 r/min。实验信号的时域波形如图4a所示。对时域信号进行包络处理，然后进行FFT变换，所得频谱图如图4b所示。

由图4a可以看出，在0.1 s内振动加速度的波峰也恰好是9个，和图2中的仿真结果完全相同。由图4b也可以看出，振动信号低频段的频率滚动体的公转频率 (9.56 Hz)、滚动体的双边冲击频率及其倍频 (94.02 Hz、188.04 Hz等)以及形成的边频 (84.46 Hz、103.58 Hz、178.48 Hz及197.6 Hz等)，与图3中的仿真结果是完全相同的。由此可证明本文所建立模型是有效的，能够从理论上解释滚动体局部故障滚动轴承的振动机理。

另外，在实验信号中，由于保持架的旋转信号和滚动体冲击信号不强，因此，时域图中的冲击特征不是非常突出，并且频谱图中边频成分并不是很明显。

图4 滚动体具有单一局部故障滚动轴承的实验结果Fig.4 Experimental results of rolling bearing with single local defect on rolling element

4 结论

通过建立滚动体具有单一局部故障的滚动轴承的动力学模型，并进行数值求解和实验验证。得出了以下结论:

(1)改进了缺陷模型，考虑了缺陷宽度以及深度在接触变形计算中的作用，使模型更加接近实际;

(2)仿真了滚动体具有单一故障轴承的振动速度曲线。并通过分析得出了其低频成分为滚动体的自转频率及其倍频、保持架的旋转频率以及由它们所形成的边频。证实了实际滚动轴承故障诊断常用的判据;

(3)通过实验对比，证实了仿真结果的可靠性和所建立模型的正确性。

［1］ RAFSANJANIA Ahmad，ABBASION Saeed．Nonlinear dynamic modeling of surface defects in rolling element bearing systems［J］．Journal of Sound and Vibration，2009，319:1150－1174．

［2］ 张中民，卢文祥等．滚动轴承故障振动模型及其应用研究 ［J］．华中理工大学学报，1997，25(3):50－53．

［3］ TANDON N，CHOUDHURY A．An analytical model for the prediction of the vibration response of rolling element bearings due to a localized defect［J］．Journal of Sound and Vibration，1997，205:275－292．

［4］ SOPANEN J，MIKKOLA A．Dynamic model of a deepgroove ball bearing including localized and distributed defects Part 1:theory ［J］．Proc．Instn．Mech．Engrs．，2003，217:201 －211．

［5］ SOPANEN J，MIKKOLA A．Dynamic model of a deepgroove ball bearing including localized and distributed defects Part 2:implementation and results ［J］．Proc．Instn．Mech．Engrs．，2003，217:213－223．

［6］ SAWALHI N，RANDALL R B．Simulating gear and bearing interactions in the presence of faults Part I:the combined gear bearing dynamic model and thesimulation of localised bearing faults［J］．Mechanical Systems and Signal Processing，2008，22:1924－1951

［7］ 杨将新，曹冲锋等．内圈局部损伤滚动轴承系统动态特性建模及仿真［J］．浙江大学学报 (工学版)，2007，41(4):551－555．

［8］ 万长森．滚动轴承的分析方法 ［M］．北京:机械工业出版社，1987．