恒电压结合牛顿法的光伏系统MPPT控制
周文源, 袁 越, 傅质馨, 惠 东, 杨 凯
(1.河海大学可再生能源发电技术教育部工程研究中心, 南京 210098;2.中国电力科学研究院,北京 100192)
恒电压结合牛顿法的光伏系统MPPT控制
周文源1, 袁 越1, 傅质馨1, 惠 东2, 杨 凯2
(1.河海大学可再生能源发电技术教育部工程研究中心, 南京 210098;2.中国电力科学研究院,北京 100192)
该文以提高跟踪速度、减少最大功率点附近功率振荡和减少误判为多重目标,提出了恒电压结合牛顿法的最大功率点跟踪策略,并利用朗伯W(LambertW)函数在光伏电池实用模型的基础上对其原理进行了理论推导和证明。该方法仅依赖于当前工作点的信息计算下一工作点的参考电压,有效地减少了误判;借助于牛顿法的良好收敛性,速度和稳定性都有提高。通过三种不同光照模式算例,与传统方法进行仿真对比,验证了方法的有效性。
光伏; 实用模型; 最大功率点跟踪; 朗伯W函数; 牛顿法; 恒定电压法; 电导增量法
在当今社会能源问题日益突出的环境下,清洁可再生能源的发展和应用成为了世界各国关注的焦点。太阳能光伏并网发电相关技术在近三十年得到了持续发展[1,2]。
光伏阵列的输出具有非线性特征,受光照强度、环境温度以及负载的影响,因此需要对其进行最大功率点跟踪MPPT(maximum power point tracking)。常用的经典MPPT控制方法有恒电压跟踪法CVT(constant voltage tracking)、扰动观察法Pamp;O(perturbation amp; observation)[3]、电导增量法INC(incremental and conductance)[4]等。经典算法有各自的优缺点[5,6],CVT法利用光伏阵列MPP的工作电压Vm与开路电压Voc存在近似比例关系这一特性进行控制,因此控制精度不高。Pamp;O法和INC法本质上都是依靠求电压变化前后工作点的功率差,找到满足dP/dU为0的点。前者采用功率差Pk-Pk-1来近似dP,而后者则是通过全微分UΔI+IΔU来近似。Pamp;O法的缺陷在于,当光照稳定时,光伏阵列的实际工作点会始终在最大功率点MPP(maximum power point)附近小幅振荡,而光照高速变化时该算法可能失效,判断得到错误的跟踪方向。尽管INC法在精度上相对Pamp;O有所提高,但仍然无法避免稳态振荡和误判的问题。
研究者针对上述传统方法的缺点,在传统方法的基础上,提出了多方面的改进,如:采用变步长法[7~9]提高跟踪速度;利用小步长扰动[10]改善MPP附近的振荡问题,也有使用较复杂的数学方法,如零均值法[11]和中心差分法[12];在处理光照剧烈变化带来的误判上,滞环比较法[13]效果较好,却存在精度和速度的矛盾。其他算法,如模糊控制[14]、优化算法[15]可实现较好的控制效果,但算法较为复杂。
基于提高跟踪速度、减少MPP附近功率振荡和减少误判的多重目标,本文对新型的MPPT方法进行了一定探索。文章首先建立光伏面板的实用仿真模型,然后借助LambertW函数推导得到光伏面板的最大功率曲线Pm(V),以此为基础利用恒电压与牛顿法结合的方法提出MPPT控制策略,并进行了理论证明。该策略采用恒定电压法确保系统的工作电压达到并超过最低参考电压,再根据当前时刻的工作点信息通过牛顿法计算出下一时刻系统的参考电压,从而逐步逼近MPP。该方法仅以当前工作点的信息作为依据,不受光照变化约束,可明显减少误判。同时,牛顿法具有较好的收敛性,在很大程度上避免了常规方法在MPP附近的振荡现象。因此,本文方法在理论上具有跟踪速度快、误判几率低、稳态振荡小的特点。
文中在光照为阶跃变化、三种不同斜率的斜坡变化和特别复杂变化的环境下,将本文方法与采用不同搜索步长的传统Pamp;O法和INC法进行了对比,通过仿真验证了方法的正确性与优势。
1 光伏电池工程实用模型
1.1 光伏电池工程实用模型的建立
光伏电池的等效电路如图1所示。
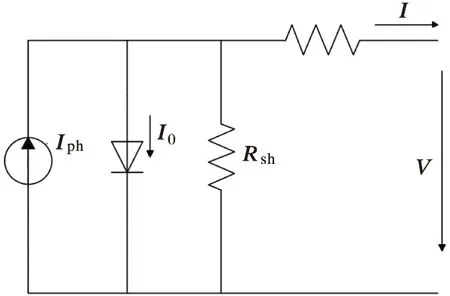
图1 光伏电池等效电路
按照图1中的电流、电压参考方向,可以得到光伏电池的I-V特性方程:
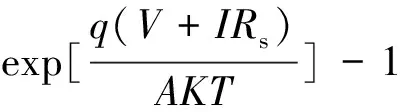
(1)
式中:Iph为光生电流,A;I0为二极管反向饱和电流,A;q为电子电荷;T为绝对温度,K;K是玻尔兹曼常数;A为二极管因子常数;Rs为串联等效电阻,Ω;Rsh为并联等效电阻,Ω;I为电池输出电流,A;V为电池输出电压,V。
式(1)中的5个主要参数,即Iph、I0、Rs、Rsh和A,与电池温度和日照强度相关,既难以确定也不是厂商提供的标准参数,因此不便于工程应用。
若在式(1)基础上,做两点近似[16~18],便可以得到光伏电池的实用I-V方程:
I=Isc{1-C1[exp(V/(C2Voc))-1]}
(2)
C1=(1-Im/Isc)exp(-Vm/(C2Voc))
(3)
C2=(Vm/Voc-1)[1n(1-Im/Isc)]-1
(4)
1.2 光伏电池实用模型的环境修正及验证
光伏电池的性能因外界温度及光强变化而不同,因此需要对式(2)进行环境修正[16~18]。引入两个补偿系数ki、kv:
ki=R[1+aΔT]/Rref
(5)
kv=[1-cΔT]1n[e+bΔR/Rref]
(6)
其中
ΔT=T-Tref
ΔR=R-Rref
式中:R为日照强度,W/m2;Rref为标准状态下的日照强度,其值为1000 W/m2;a,b,c为修正系数,其取值参见文献[16]。修正后的性能参数为
(7)
经修正,式(2)变为:
(8)
将本文采用的STP280-24/Vd[19]光伏电池实用模型的I-V特性和P-V特性与厂商提供的实测曲线在不同日照强度下进行对比,以全面验证模型的正确性。该面板在1000 W/m2,25 ℃标准情况下的4个基本参数为Im=7.95 A,Isc=8.33 A,Vm=35.2 V,Voc=44.8 V。
通过图2的对比结果可以看出,基于环境修正的光伏电池实用模型与实际输出非常接近,误差能够满足工程计算需要,因此将此模型应用于仿真可以很好地拟合光伏面板的实际工作特性,为光伏系统的设计与优化带来便利。
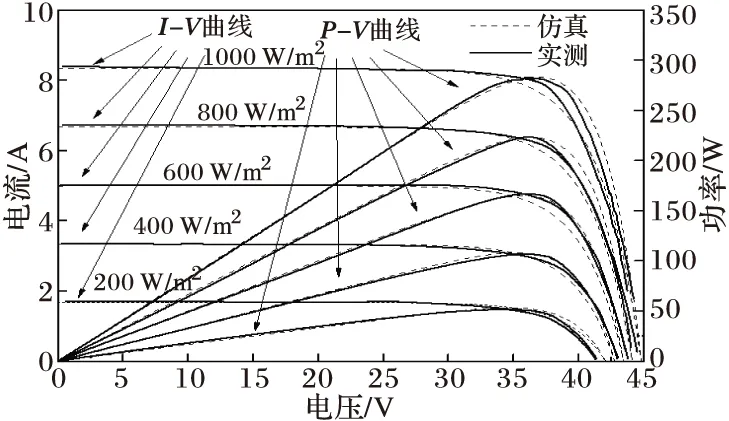
图2 不同日照强度下光伏电池仿真结果与实测结果对比
2 恒电压结合牛顿法MPPT
2.1LambertW函数[20]求解最大功率曲线
在MPP处有dP/dV=0,展开得
dP/dV=VdI/dV+I=0
(9)
将式(8)代入(9)可得
(10)
式(10)是一个超越方程,虽然可采用牛顿法迭代进行求解,但只能求得数值解,无法直接求出V的初等函数表达式。通过观察式(10)的形式,本文选用LambertW函数来表达MPP处的电压。LambertW函数是方程(11)的解,是一个超越函数,它的数值解可借助数学软件Mapple,Matlab或Mathematica获得。
z=w(z)ew(z)
(11)
将式(10)整理为式(11)的LambertW函数标准形式,即:w(z)中含有V,z项不含V。如式(12)所示:
(12)
记
z=(1+C1)e/C1
(13)
由于z为正数,必然大于-1/e,因此w(z)具有唯一解,将z的表达式代入w(z),整理得到
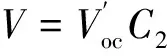
(14)
V=λ1n(e+bΔR/Rref)
(15)
λ=VocC2[1-c(ΔT)]W
(16)
W=lambertw[(1+C1)e/C1]-1
(17)
这样由式(15)便可得到MPP处,电压V和辐射强度R的关系,
R=Rref{[exp(V/λ)-e]/b+1}
(18)
在求P=VI时,考虑式(18),可化简得到:
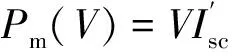
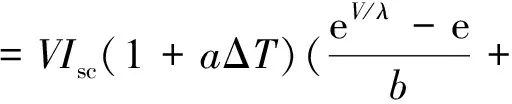
1){1-C1[eW-1]}=αV+βVeV/λ
(19)
式中:
α=β(b-e)
β=Isc(1+aΔT){1-C1[eW-1]}/b
式(19)就是最大功率曲线的显性表达式,该式中的参数有两个:α和β,它们仅仅与光伏面板自身的4个基本参数有关。曲线图形如图3所示。
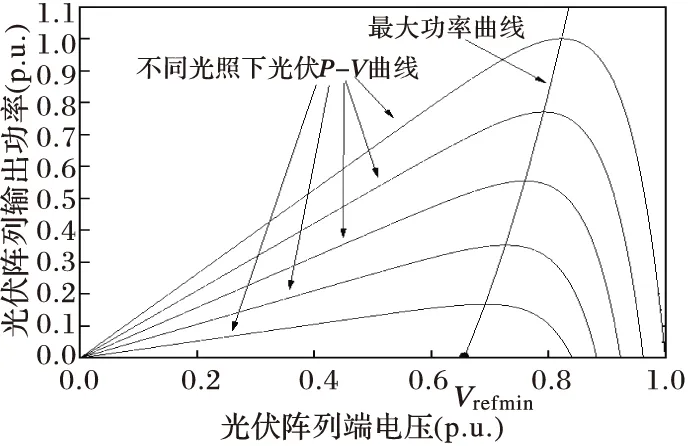
图3 光伏面板最大功率曲线
2.2 牛顿法MPPT的理论基础
由于式(19)已经表示出了在外界环境变化下MPP处功率与电压的关系,本文考虑利用该关系进行MPPT控制。
首先,注意到图3中最大功率曲线与电压轴有交点,说明即使在日照强度极低、光伏面板发出功率接近于0时,其最优工作电压仍然是一个相对较大的值。因此在寻优时,便可采用此电压作为最低电压参考值,记为Vrefmin,并采用恒定电压法控制。这样可以明显提高启动时的跟踪速度。
其次,当系统的工作电压大于Vrefmin时,任意确定光强下的P-V曲线与最大功率曲线仅有一个交点,若两条曲线的差满足牛顿法的收敛条件,则可将问题转化为牛顿法求零点的问题。定义f(V)为两者之差:
f(V)=Pm(V)-P(V)
V∈[Vrefmin,VM]
(20)
其中,VM是日照强度为标准状况3倍时的开路电压,因实际测量中出现超过标准状况3倍的日照强度极为罕见,故而该上限具有实用性。下面简略证明其满足牛顿法的收敛条件:
1)由图3,显然有
f(Vrefmin)×f(VM)lt;0
(21)
2)对f(V)求一次和二次导数,得到
(22)
(23)
因λ,β,C1,C2都是正数,所以f″(V)gt;0,显然在定义域上保号,同时说明f′(V)单调递增。若能证明f′(Vrefmin)为正数,则可证明f′(V)在定义域上保号。考虑到Pm(Vrefmin)的值为0,由式(19)有
Vrefmin=λln(-α/β)
(24)
将式(24)代入式(22)计算f′(Vrefmin):
f′(Vrefmin)=-α1n(-α/β)+
b)(1-C1eW)-R/Rref]
(25)
式(25)中的可变参数只有C1和R,根据不等式证明的放缩法,将C1放大到10-4并将R取定义域上限3Rref后一起代入式(25),可推得:
f′(Vrefmin)gt;0.752Isc(1+aΔT)gt;0
(26)
因此,综合1),2)可判定f(V)=0在区间[Vrefmin,VM]上满足牛顿法的收敛条件。
2.3 恒电压结合牛顿法MPPT
本文在系统工作电压高于Vrefmin时采用牛顿法核心思想进行寻优,寻优过程如图4所示。
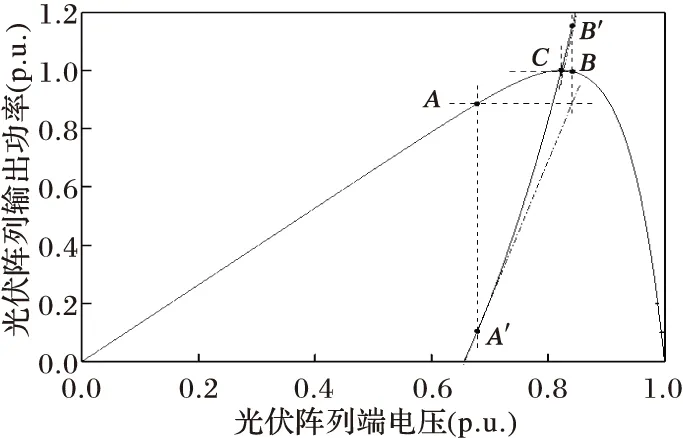
图4 牛顿法MPPT寻优流程
根据图4对算法做几何上的描述:若初始工作点在A,延A点做垂线与Pm(V)曲线相交得到A′点,过A′作Pm(V)曲线的切线并与过A的水平线相交,交点处的横坐标便是下一点B的横坐标,如此类推可得到B′点和C点。根据上述理论推导可知:若n时刻测得工作点的电压为Vn功率为Pn,则系统n+1时刻工作点的电压表达式为
(27)
算法的整体流程图见图5。
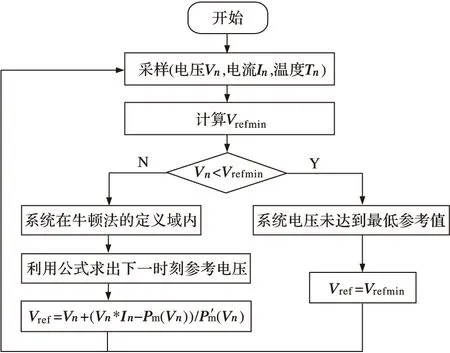
图5 恒电压结合牛顿法MPPT控制框图
3 仿真分析
为验证本文提出的MPPT算法的有效性,在Matlab/Simulink环境中对其进行仿真验证。电池模型采用STP280/24V的工程实用模型,分别使用电导增量法、扰动观察法及本文方法,在不同光照条件下进行仿真,对比其最大误差和平均效率。
仿真采用了3种不同的光照环境以便全面对比三种方法在不同情况下的性能,如图6。
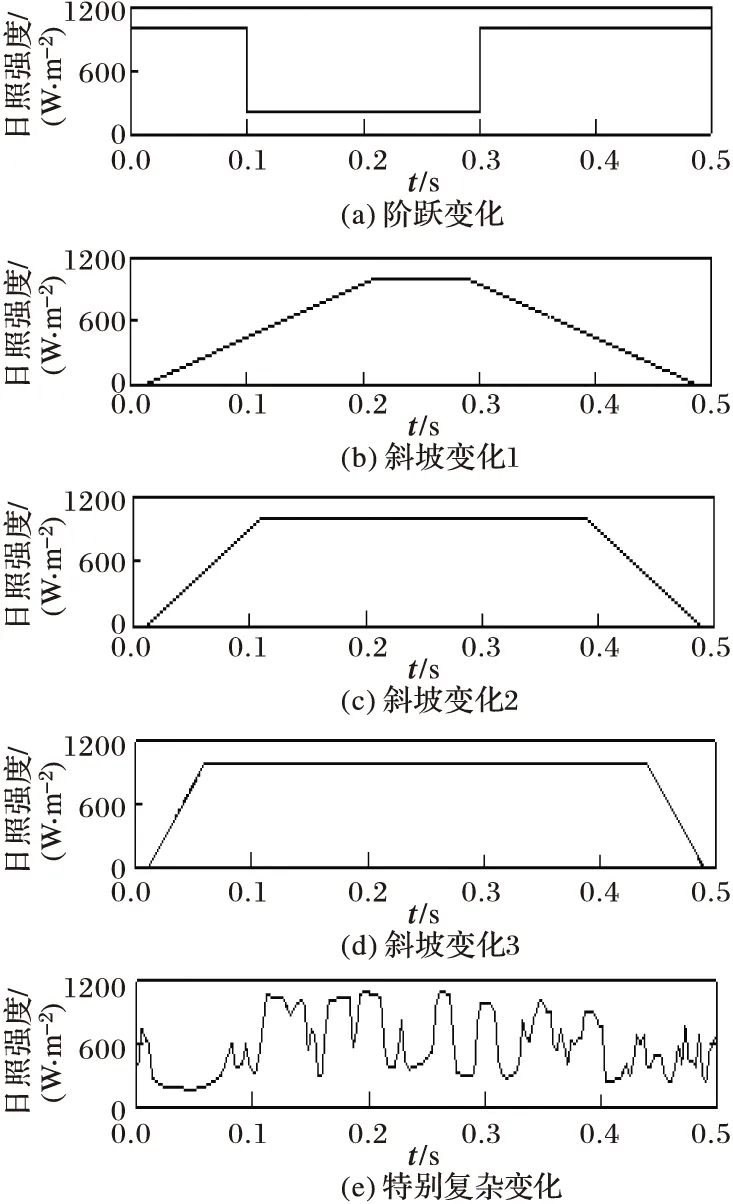
图6 仿真采用的日照曲线
首先是常用的阶跃变化,该变化可模拟云层遮挡时造成的光照突然跌落。初始光照正常,为1000 W/m2,0.1 s时由于云层遮挡,突然跌落到200 W/m2,0.3 s后又恢复正常。其次是三种斜坡变化,该变化可模拟太阳初升和落山时日照的均匀增加和减少。初始光照强度为0 W/m2,0.01 s时起依照不同斜率均匀增加到1000 W/m2后,保持一定时间后又按照之前的斜率负值逐渐回到0 W/m2。最后是一段变化极不规则的日照曲线,该数据截取自美国国家可再生能源实验室(NREL)的某日实测日照数据[21]。
图7是阶跃变化时三种仿真结果的对比图。从图中的功率曲线可看出,日照强度变化时采用本文方法可更为迅速地找到MPP;自参考电压曲线中可看出,本文方法的参考电压在光照稳定后几乎不变,而两种传统方法的参考电压则是在最优值附近波动,因而会造成小幅功率振荡,导致功率损失。
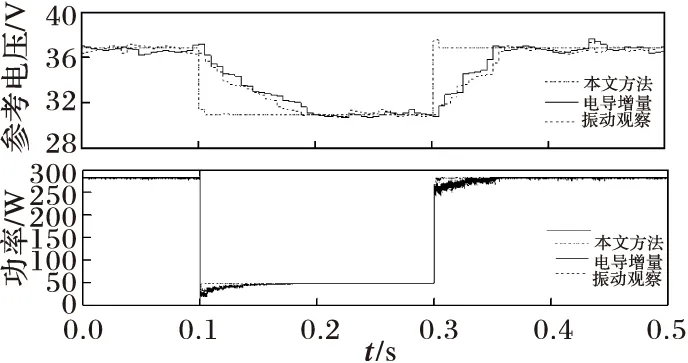
图7 阶跃变化时三种方法仿真结果
斜率分别为5000 W·m-2/s,10000 W·m-2/s和20000 W·m-2/s的斜坡信号下的仿真结果如图8。通过观察图中参考电压的曲线可以发现,在光照缓慢增加时,传统方法时常出现误判,该结论也反映在功率曲线上。有两点值得注意的是,传统方法在上坡时斜率越小跟踪失误反而越大,下坡时的跟踪效果则均不理想。本文方法在各种斜率下都能随着光照的变化跟踪到最佳工作电压。
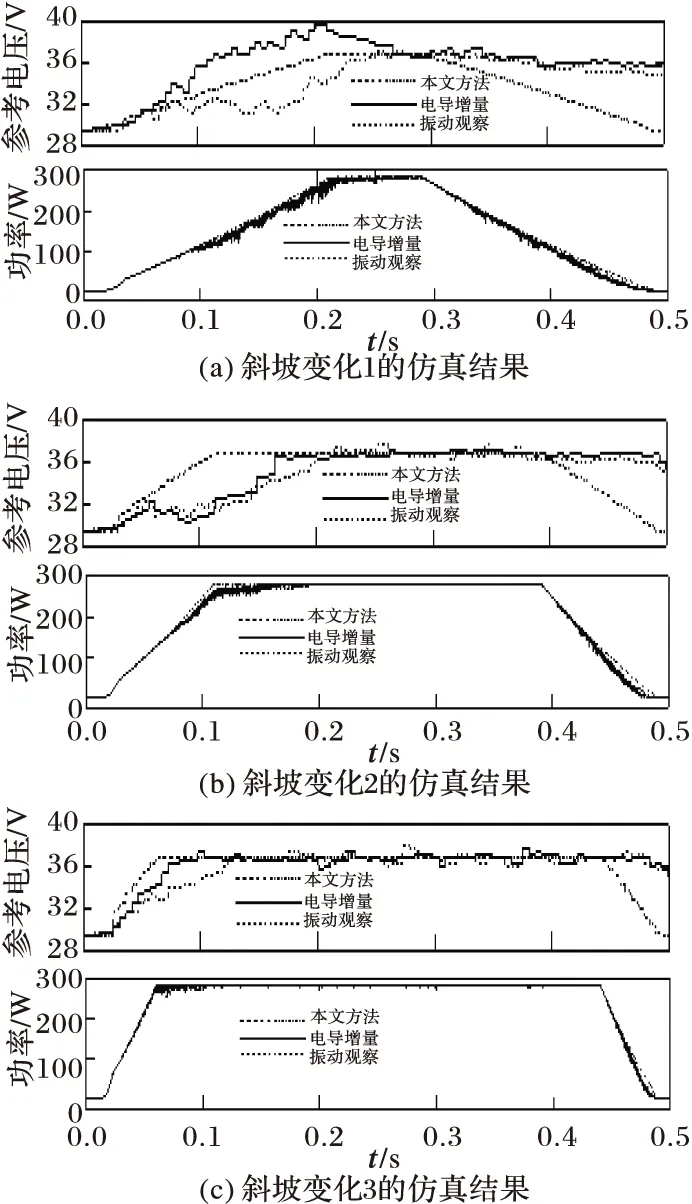
图8 不同斜率的斜坡变化下三种方法的仿真结果
特别复杂变化的结果如图9。由于光照很不规则,且变化很快,传统方法跟踪效果并不理想,误判较多。从参考电压图中可以清晰地看出只有本文方法的参考电压是随着光照变化的趋势而改变的。从功率变化图中可以发现:在某些时段,传统方法的出力甚至不及本文方法的一半。
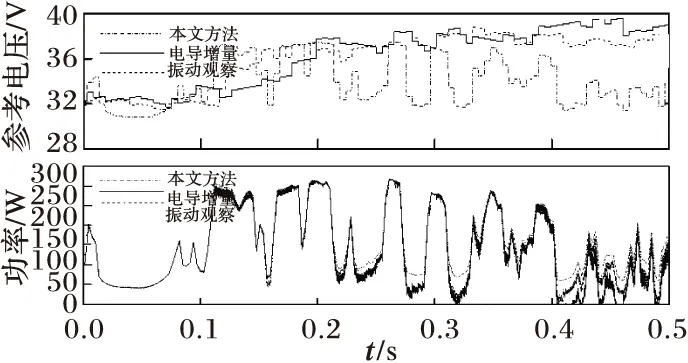
图9 特别复杂变化时三种方法仿真结果
搜索步长对传统方法的性能有较大影响,搜索步长大可以加快跟踪速度,但稳态时可能出现较大功率振荡,搜索步长过小则会导致速度较慢。图7~图9仅展示了搜索步长为0.1 V时的传统方法的结果,并不能全面体现传统方法的性能。表1列出了前述三种日照变化类型下,本文方法与采用了不同搜索步长的传统方法的全域平均效率、稳定域最大误差和稳定域平均效率,以便将传统方法在不同搜索步长下的性能与本文方法进行对比。其中全域和稳定域做如下界定:
全域T全域=[0 s,5 s]
稳定域T阶跃=[0.15 s,0.3 s]
T斜坡1=[0.26 s,0.29 s]
T斜坡2=[0.16 s,0.39 s]
T斜坡3=[0.11 s,0.44 s]
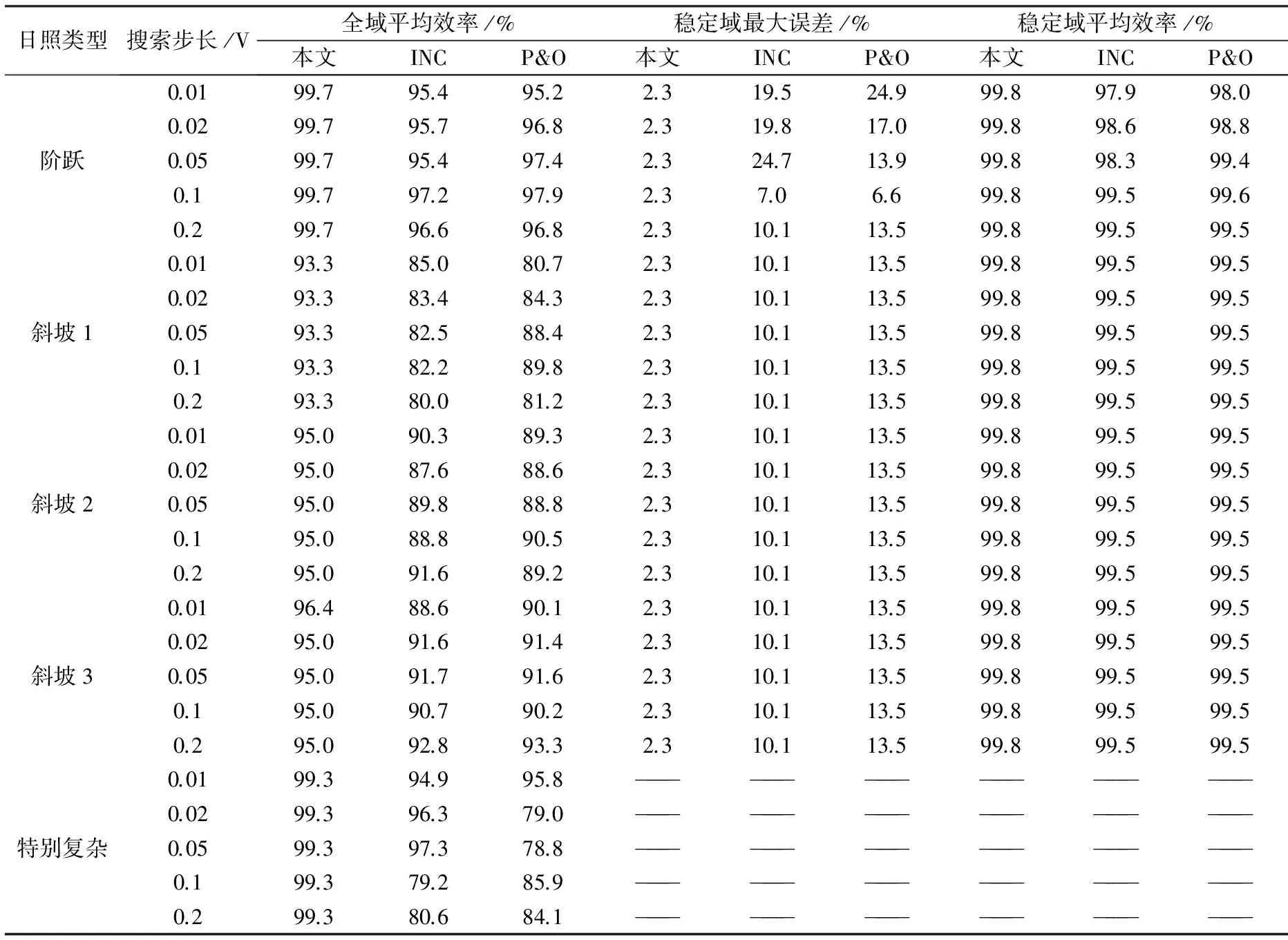
表1 多日照类型、多种搜索步长下三种方法的全域平均效率、稳定域的最大误差和平均效率对比
全域的时域区间就是整个仿真区间;稳定域不仅是指日照稳定,同时也顾及到系统响应时间的问题,故其区间为日照稳定后0.05s至下一次改变时。特别复杂变化不含稳定域。
从表1中数据可以看出,在日照类型依次为阶跃、斜坡1、斜坡2、斜坡3和特别复杂变化时,本文方法的全域平均效率达到99.7%,93.3%,95.0%,96.4%,99.3%,均高于计及多种搜索步长的传统方法的平均效率最优值97.9%,89.8%,91.6%,93.3%,97.3%。稳定域的最大误差方面,本文方法在各种日照类型下均能始终保持在2.3%,优于传统方法的最优值6.6%,稳定域的平均效率稳定达到99.8%,也优于传统方法的最优值99.5%。另外,需要指出本文方法没有需要调节的参数,其搜索步长由公式自然导出,而传统方法为达到最优值往往需要对搜索步长进行反复试凑,且不能保证一种日照类型中找到的最优值在其他环境中同样适用。
4 结语
本文在建立了光伏电池实用模型的基础上,利用LambertW变化推导出了光伏面板最大功率曲线Pm(V),提出了恒电压与牛顿法结合的MPPT控制策略,并对牛顿法的适用性做了证明。
在日照强度为阶跃变化、斜率不同的三种斜坡变化和特别复杂变化的环境中,将本文方法与采用多种搜索步长的传统Pamp;O法和INC法进行了较为全面的仿真对比分析。仿真结果表明,本文提出的恒电压结合牛顿法MPPT具有响应速度快、稳态振荡小、误判较少、无参数调节过程的特点,较好地解决了传统方法多方面的不足,并且能够最大程度地提升系统效率、降低功率损失,具有良好的实用价值。
[1] 王飞,余世杰,苏建徽,等(Wang Fei,Yu Shijie,Su Jianhui,etal).太阳能光伏并网发电系统的研究(Research on photovoltaic grid-connected power system)[J].电工技术学报(Transactions of China Electrotechnical Society), 2005,20(5):72-74,91.
[2] 程军照,李澍森,张腾飞(Cheng Junzhao, Li Shusen, Zhang Tengfei).多路并网光伏发电系统的仿真与分析(Simulations and analysis on a multi-branch grid-connected photovoltaic system)[J].电力系统及其自动化学报(Proceedings of the CSU-EPSA),2009,21(4):58-62.
[3] Femia N,Petrone G,Spagnuolo G,etal.Optimization of perturb and observe maximum power point tracking method[J]. IEEE Trans on Power Electronics,2005,20(4):963-973.
[4] Hussein K H,Muta I,Hoshino T,etal.Maximum photovoltaic power tracking : an algorithm for rapidly changing atmospheric conditions [J].IEE Proceedings-Generation,Transmission and Distribution,1995,142(1):59-64.
[5] Esram T,Chapman P L.Comparison of photovoltaic array maximum power point tracking techniques[J]. IEEE Trans on Energy Conversion,2007,22(2):439-449.
[6] 陈剑,赵争鸣,袁立强,等(Chen Jian,Zhao Zhengming,Yuan Liqiang,etal).光伏系统最大功率点跟踪技术的比较(Comparison of maximum power point tracking technologies for photovoltaic power systems)[J].清华大学学报(自然科学版)(Journal of Tsinghua University (Science amp; Technology)),2010,50(5):700-704.
[7] Liu Fangrui,Duan Shanxu,Liu Fei,etal.A variable step size INC MPPT method for PV systems[J]. IEEE Trans on Industrial Electronics,2008,55(7):2622-2628.
[8] 刘邦银,段善旭,刘飞,等(Liu Bangyin,Duan Shanxu,Liu Fei,etal).基于改进扰动观察法的光伏阵列最大功率点跟踪(Photovoltaic array maximum power point tracking based on improved perturbation and observation method)[J].电工技术学报(Transactions of China Electrotechnical Society),2009,24(6):91-94.
[9] 黄舒予,牟龙华,石林(Huang Shuyu , Mu Longhua, Shi Lin).自适应变步长MPPT算法(Adaptive variable step size MPPT algorithm)[J].电力系统及其自动化学报(Proceedings of the CSU-EPSA),2011,23(5):26-30.
[10]张超,何湘宁(Zhang Chao,He Xiangning).短路电流结合扰动观察法在光伏发电最大功率点跟踪控制中的应用(Short-current combined with perturbation and observation maximum-power-point tracking method for photovoltaic power systems)[J].中国电机工程学报(Proceedings of the CSEE),2006,26(20):98-102.
[11]董密,杨建,彭可,等(Dong Mi,Yang Jian,Peng Ke,etal).光伏系统的零均值电导增量最大功率点跟踪控制(Zero average incremental conductance maximum power point tracking control for photovoltaic system)[J].中国电机工程学报(Proceedings of the CSEE),2010,30(21):48-53.
[12]Xiao Weidong,Dunford William G,Palmer Patrick R,etal.Application of centered differentiation and steepest descent to maximum power point tracking[J]. IEEE Trans on Industrial Electronics,2007,54(5):2539-2549.
[13]Hsiao Ying-Tung,Chen China-Hong.Maximum power tracking for photovoltaic power system[C]// The 37th IAS Annual Meeting, Pittsburgh,USA:2002.
[14]Wu Tsai-Fu, Chang Chien-Hsuan, Chen Yu-Hai.A fuzzy-logic-controlled single-stage converter for PV-powered lighting system applications[J]. IEEE Trans on Industrial Electronics,2000,47(2):287-296.
[15]贺凡波,赵争鸣,袁立强(He Fanbo,Zhao Zhengming,Yuan Liqiang).一种基于优化算法的光伏系统MPPT方法(A MPPT method for photovoltaic systems based on optimization algorithms)[J].电力电子技术(Power Electronics),2009,43(10):11-13.
[16]苏建徽,余世杰,赵为,等(Su Jianhui,Yu Shijie,Zhao Wei,etal).硅太阳电池工程用数学模型(Investigation on engineering analytical model of silicon solar cells)[J].太阳能学报(Acta Energiae Solaris Sinica),2001,22(4):409-412.
[17]焦阳,宋强,刘文华(Jiao Yang,Song Qiang,Liu Wenhua).光伏电池实用仿真模型及光伏发电系统仿真(Practical simulation model of photovoltaic cells in photovoltaic generation system and simulation)[J].电网技术(Power System Technology),2010,34(11):198-202.
[18]Singer S,Rozenshtein B,Surazi S.Characterization of PV array output using a small number of measured parameters[J].Solar Energy,1984,32(5):603-607.
[19]尚德太阳能电力有限公司.280瓦多晶硅太阳能组件 STP280-24/ Vd数据手册[EB/OL]. http://old.suntech-power.com/images/stories/2010_datasheets/CN/stp280_24vd_cn_no1.pdf, 2011.
[20]许佳雄,姚若河,耿魁伟(Xu Jiaxiong,Yao Ruohe,Geng Kuiwei).用LambertW函数求解太阳能电池的串联电阻(Determination of series resistance of solar cells using LambertW-function)[J].华南理工大学学报(自然科学版)(Jounal of South China University of Technology (Natural Science Edition)),2010,38(6):42-45.
[21]NREL.Measurement and instrumentation data center (MIDC) [EB/OL]. http://ww.nrel.gov/midc, 2100.
周文源(1987-),男,硕士研究生,研究方向为可再生能源发电技术。Email:wen-yuan.zhou@hotmail.com
袁 越(1966-),男,博士,教授,博士生导师,研究方向为可再生能源发电技术、分布式发电与供电技术、微型电网、智能电网等。Email:yyuan@hhu.edu.cn
傅质馨(1983-),女,博士,研究方向为智能电网、可再生能源发电技术。Email:zhixinfu@hhu.edn.cn
ConstantVoltageTrackingCombinedwithNewtonMethodMPPTControlforPhotovoltaicSystem
ZHOU Wen-yuan1, YUAN Yue1, FU Zhi-xin1, HUI Dong2, YANG Kai2
(1. Research Center for Renewable Energy Generation Engineering, Ministry of Education,Hohai University, Nanjing 210098, China;2. China Electric Power Research Institute, Beijing 100192, China)
This paper proposed a novel multi-objective maximum power point tracking (MPPT) strategy combined constant voltage tracking and Newton method in order to improve tracking speed, minimize the power oscillation near maximum power point (MPP) and reduce erroneous results. A theoretical derivation and a demonstration based on practical photovoltaic (PV) cell model were also given by using LambertW function. The proposed method only uses the information of the actual working point to calculate the reference voltage of the next working point, thus the erroneous result is thus reduced. With the help of Newton method's good convergence, the proposed method shows a better tracking speed and less oscillation. Numerical simulations were conducted based on various radiation types to test the effectiveness of the proposed method. The results validate its effectivity and efficiency.
photovoltaic (PV) cell; practical model; maximum power point tracking(MPPT); LambertW function; Newton method; constant voltage tracking; incremental and conductance(INC)
TM615
A
1003-8930(2012)06-0006-08
2011-12-20;
2012-02-04
国家科技支撑计划“风光储输示范工程关键技术研究”课题七“电池储能大规模系统集成技术研究”(2011BAA07B07)

