七孔探针测量剪切流场的误差分析和实验验证
马兴宇,明 晓
(南京航空航天大学 空气动力学系,江苏 南京210016)
0 引 言
七孔探针是一种测量流场某处速度的大小、方向、总压和静压的压力探头。作为一种精度高、可靠性好、测量角度范围大、结构简单的测量技术,七孔探针适用于大剪切、大偏角流场的测量,例如射流、钝体尾流、飞机翼尖涡等复杂流动。20世纪80年代,NASA和Ames研究中心联合研发了七孔探针及其标定方法,利用多项式代数方法拟合系数矩阵,进行误差分析[1]。当前,七孔探针广泛应用于流动分离[2]、复杂旋涡测量[3-5]、弹射救生[6]等领域。
七孔探针作为一种接触性测量技术,通常在均匀流场中进行标定。然而,探针的锥形头具有有限尺寸(直径约3mm~10mm),在测量复杂流场——例如剪切流动时——由于各个压力孔空间位置的差异,而造成各孔感受的压力不同,所测量的速度和角度都会产生误差。如图1所示,由于上方的孔所感受的压力比下方的孔所感受的压力大,使得角度的测量产生误差,同时也引起速度测量的误差。
本文利用数值模拟的方法,研究了七孔探针在剪切流场中气动特性,并分析了速度梯度、七孔探针直径、滚转角等因素产生的误差。在实验中,利用七孔探针测量圆管射流,验证了数值分析的结果。

图1 七孔探针测量剪切流场示意图Fig.1 The seven-hole probe in shearing flow field
1 七孔探针基本原理
对于七孔探针,根据七个压力孔的压力高低,将流动空间划分为七个区。以压力最高的孔编号为名。中心第七孔所对的流动空间称为内区,其它六个区称为外区。如图2所示。
图3所表示七孔探针的坐标系。在小流动角的情况下(内区),采用迎角α和侧滑角β来确定气流方向。迎着气流看,右侧滑为正。对于大流动角(外区),利用俯仰角θ和方位角φ,θ是速度向量与探头轴线之间的夹角,始终为正。φ是速度向量在YZ平面内的投影与Z平面之间的夹角,逆时针为正。
校准方法采用最小二乘法进行曲线拟合,采用四次多项式(1)来确定各区参数

图2 七孔探针流动分区示意图Fig.2 The seven zones of the seven-hole probe

图3 七孔探针坐标系Fig.3 The coordinates of the seven-hole probe
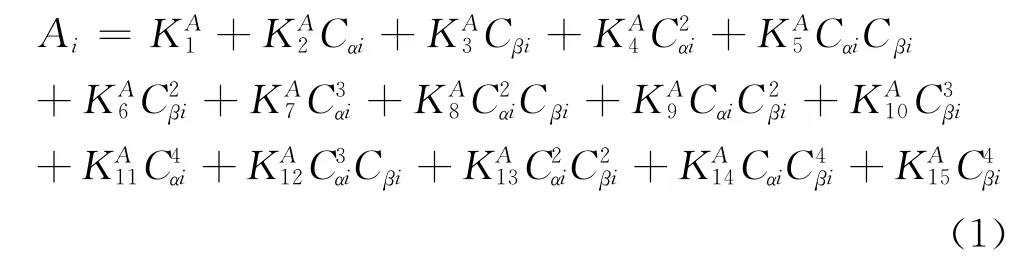
对小流动角(内区):A=α、β、Co、Cq;
对大流动角(外区):A=θ、φ、Co、Cq;
KA是校准系数,一根探针共有420个系数,这些系数通过校准得到。
每个点数据含七个压力值。从探针各孔测得的压力值及最大压力孔值,整理得到Cα,Cβ,Co,Cq(内区)和Cθ,Cφ,Co,Cq(外区),代入式(1)式中。也可用矩阵形式(2)表示:

简写为:

为得到校准系数[K],采用转置矩阵法直接求解
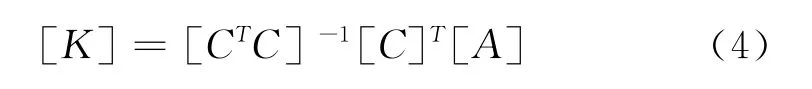
式中[C]T为[C]的转置矩阵。
2 七孔探针数值校准
2.1 建立模型
通过计算流体力学方法对七孔探针进行校准,确定其系数矩阵。首先建立模型。七孔探针尺寸如图4所示。

图4 七孔探针几何外形Fig.4 Geometry of the seven-hole probe
2.2 数值校准的参数范围
七孔探针数值校准过程中,变量只有俯仰角θ和滚转角φ(内区为迎角α和侧滑角β)。由于模型是对称的,本文采用21个俯仰角(从0°到80°,增量为4°)和7个滚转角(从0°到30°,增量为5°),共147个角度组合。标定在均匀来流中进行,来流速度大小30m/s。
2.3 精度分析
拟合系数矩阵,计算拟合标准偏差,如表1所示。本文中数值方法的校准精度比较高。因此三维模型和系数可以进行下一步平行剪切流场的测量。

表1 数值标定精度Table 1 The precision of the calibration by numerical method
3 七孔探针测量平行剪切流场的数值模拟
本章节,利用数值模拟的方法,分别探讨速度梯度、探针直径、探针滚转角对于测量的影响。这里定义速度梯度k,单位为;定义探针直径d,单位为mm;定义探针滚转角φ,单位为°。
3.1 速度梯度的影响
本文采用10个速度梯度(从k=0.1到k=1.0,增量为0.1)作为来流条件,方向与七孔探针轴线平行,探针直径4mm,滚转角φ=0°,一共10个算例。每个算例采集1-7孔压力值,分别得到速度大小和方向,计算结果如图5、图6所示。

图5 剪切流场中速度误差Fig.5 The magnitude error in shearing flow field

图6 剪切流场中角度误差Fig.6 The angle error in shearing flow field
计算结果表明,随着速度梯度的增大,即流场剪切的程度增大,探针测量速度大小和角度会出现系统误差。在平行剪切流场中,由于位于最高处1号孔和位于最低处的4号孔所处位置的差异,感受到不同的压力值,因此测量结果会出现误差。表2分析了在不同速度梯度下,七孔探针测量速度大小和角度产生的误差。
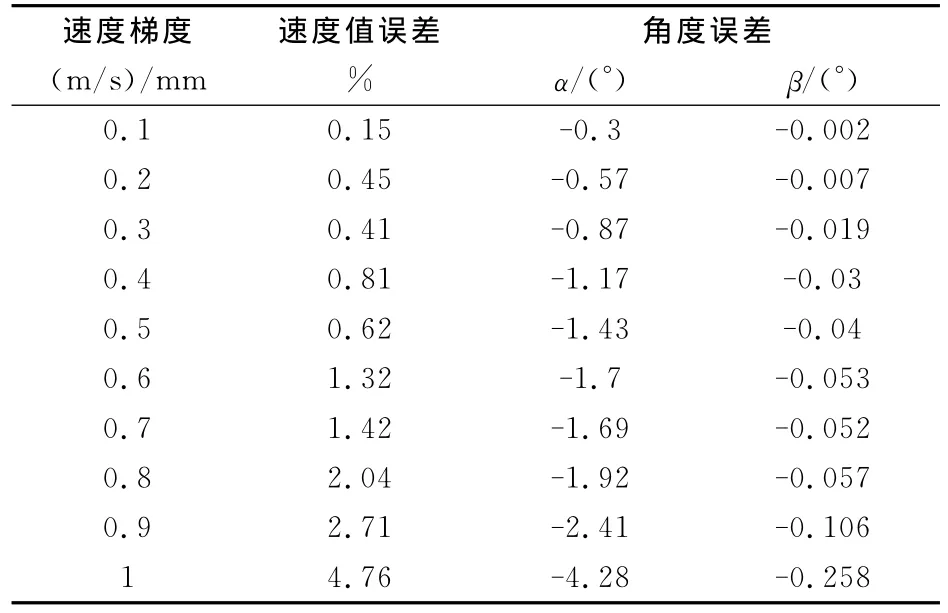
表2 速度梯度影响的误差分析Table 2 Error results from the velocity gradient
通常情况下,如果要求直径为4mm的七孔探针测量速度大小误差不大于1%,角度误差约为1°。那么,对于速度梯度小于等于0.3(m/s)/mm的剪切流场,采用直径4mm七孔探针可满足测量要求。
此外,对比速度值和角度误差可以判断,随着速度梯度的增加,相比速度值误差,角度误差首先超出精度允许的范围,即角度测量的敏感性更大。只有角度测量满足精度要求,七孔探针的测量结果才准确,下文主要讨论角度误差对精度的影响。
3.2 探针直径的影响
本文采用10个速度梯度(从k=0.1到k=1.0,增量为0.1)作为来流条件,方向与七孔探针轴线平行,探针直径4mm,6mm,滚转角φ=0°。每个算例采集1-7孔压力值,分别得到速度大小和方向,计算结果如图7、图8所示。

图7 速度误差随探针直径的变化Fig.7 Variation of the magnitude error of different diameters
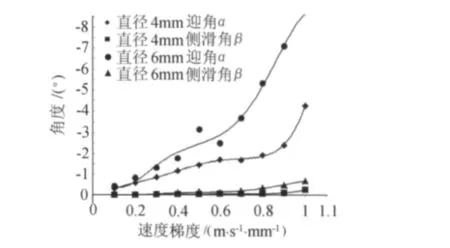
图8 角度误差随探针直径的变化Fig.8 Variation of the angle error of different diameters
表3分析了在不同探针直径下,七孔探针测量角度产生的误差。
计算结果表明,随着直径的增大,探针测量的系统误差也会增大。对于速度梯度小于等于0.3(m/s)/mm的剪切流场,采用直径4mm七孔探针可满足测量要求。对于速度梯度小于等于0.20(m/s)/mm的剪切流场,采用直径6mm七孔探针可满足测量要求。
本文定义“临界直径D”,为测量中满足精度要求的最大探针直径。在确定速度梯度的剪切流场测量中,必须选用小于等于“临界直径D”的探针,才能保证测量精度。所以,根据计算结果可知,对于速度梯度为0.25(m/s)/mm的流场,临界直径D=6mm,对于速度梯度为0.35(m/s)/mm的流场,临界直径D=4mm。
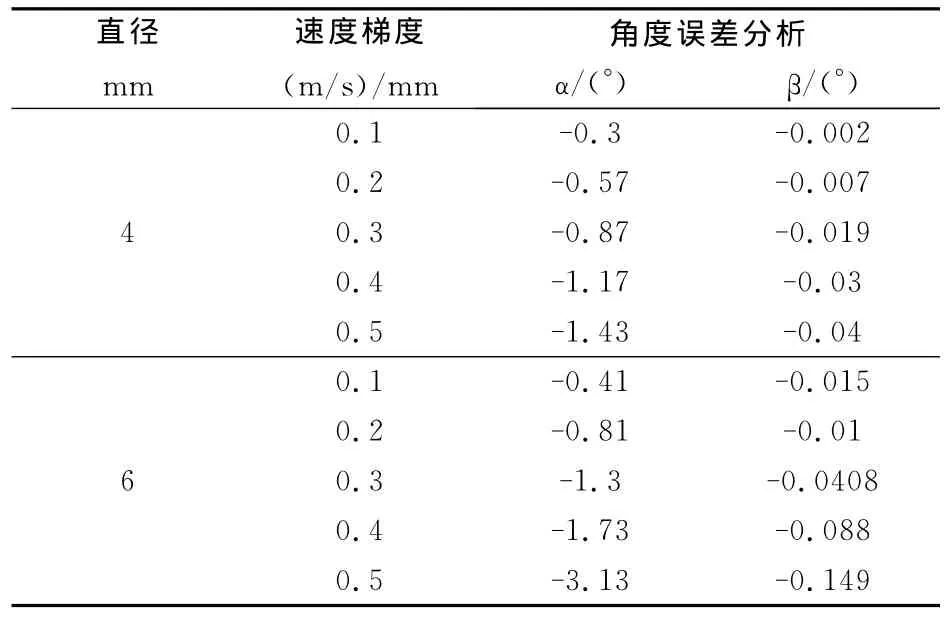
表3 直径影响的误差分析Table 3 Error results from the diameter
3.3 探针滚转角的影响
采用4个滚转角(从φ=0°到φ=30°,增量为10°),10个速度梯度(从k=0.1到k=1.0,增量为0.1)作为来流条件,方向与七孔探针轴线平行,探针直径4mm,一共40个算例。每个算例采集1-7孔压力值,分别得到速度大小和方向,计算结果如图9、图10所示。

图9 仰角测量误差随探针滚转角的变化Fig.9 Error of the angle of attack at different roll angles

图10 侧滑角测量误差随探针滚转角的变化Fig.10 Error of the angle of yaw at different roll angles
表4分析了在七孔探针不同的滚转角状态下,七孔探针测量角度产生的误差。

表4 滚转角影响的误差分析Table.4 Error results from the angle of roll angle
计算结果表明,不同的滚转角位置,会不同程度造成探针测量角度会出现系统误差。
3.4 七孔探针误差分析三维示意图
对于角度误差随探针直径d和速度梯度k的变化关系,由如下图11表示。图中z坐标轴表示角度误差,平面坐标x、y轴分别表示速度梯度和探针直径。一般七孔探针角度误差小于1°,即小于1°的平面上的测量结果是满足测量精度要求的。对于给定的剪切流场,选用七孔探针尺寸应小于“临界直径”,才能满足精度要求。
4 七孔探针测量平行剪切流场的实验研究
为了验证数值模拟方法进行误差分析工作,本节中,选用典型的剪切流场圆管射流进行实验研究。利用有限尺寸的七孔探针测量不同速度梯度的剪切流动。
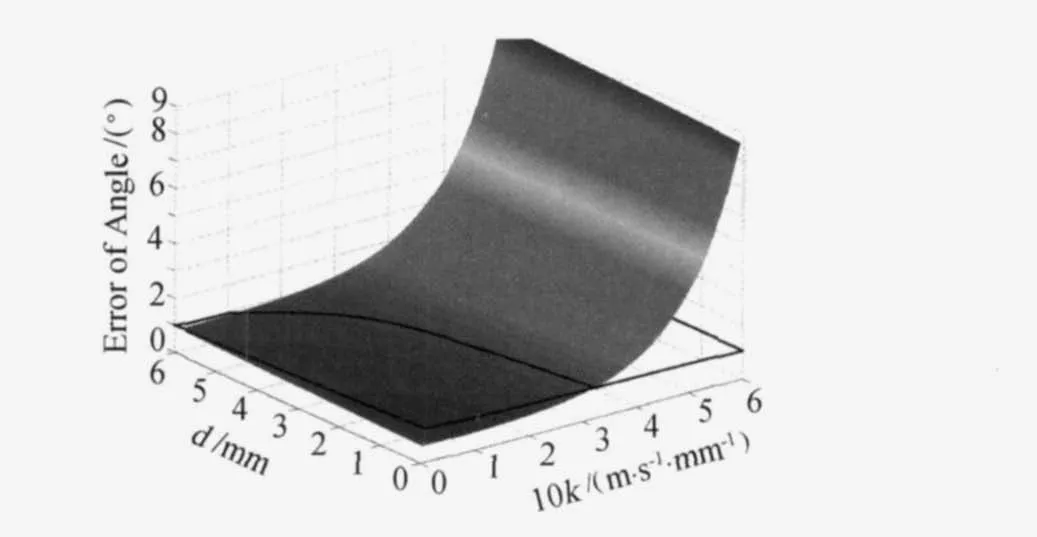
图11 七孔探针误差分布示意图Fig.11 The distribution of the error
4.1 实验模型与设备
实验在南京航空航天大学流体力学系进行。圆管由有机玻璃材料制成,长度3m,直径64mm,壁厚2mm。圆管入口连接离心式风机作为气源,出口与外界大气连通,气体流量约0.08kg/s,如图12所示。实验所用七孔探针系数矩阵已标定,直径6mm,滚转角φ=0°,轴线与圆管中心线平行。固定在支架上并可以由游标卡尺测量垂直位置。探针头部与圆管出口平面垂直,距离64mm。如图13所示。

图12 七孔探针和圆管Fig.12 The seven-hole probe and the pipe

图13 实验装置示意图Fig.13 Seven-hole probe in the shearing flow field
4.2 实验数据采集与处理
本节中,分别利用总压管和七孔探针垂直扫描测量圆管出口流场。保持滚转角φ=0°。圆管流量恒定。七孔探针(或总压管)保持与圆管中心线平行,由圆管中心为原点,向下为正,相邻点间隔2mm。
气流从圆管出来后,成为射流,具有一定扩张角,速度方向不平行,存在角度α0,满足二维圆形射流流场特征[7],角度α0分布如图14所示。
4.3 实验结果及讨论
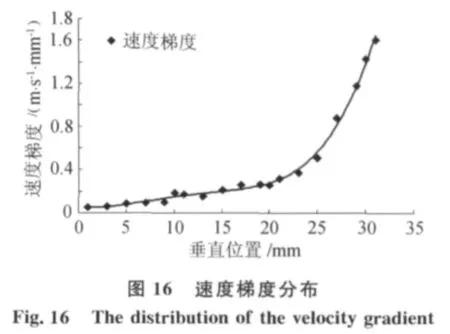
图15为总压管测量的速度分布,所谓速度大小的基准。由此计算出圆管出口速度梯度的分布,如图16所示。
七孔探针测量与总压管测量结果相对比,如图17所示,表示在当前流场中,七孔探针对速度大小、总压和静压的测量基本准确。


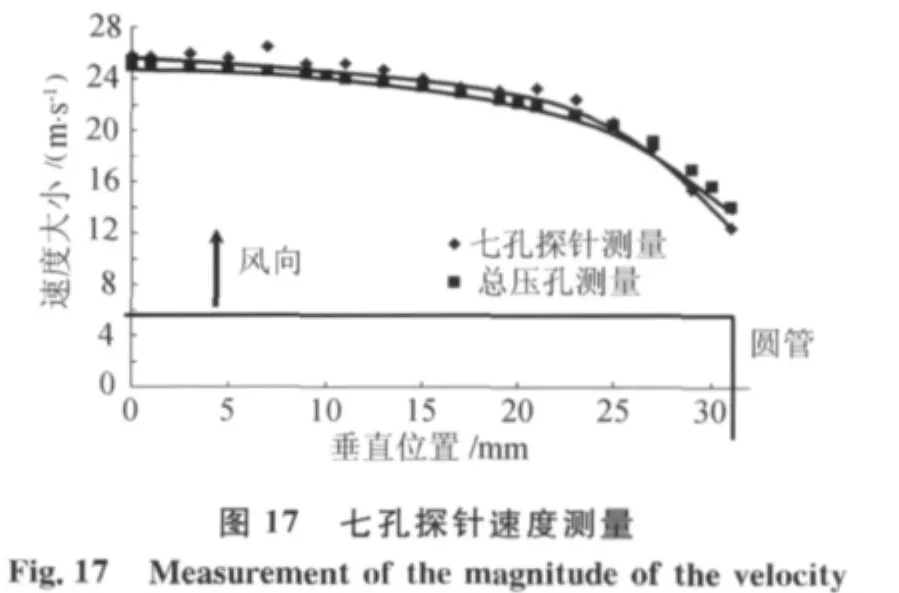
对于角度测量,比较实验和计算结果,图18所示,计算的结果偏理想。因为计算的模型无加工误差,实验中的七孔探针存在加工误差。表5分析了在实验中,测量角度产生的误差。

图18 七孔探针角度测量Fig.18 Measurement of the angle of the velocity
实验结果表明,系统误差主要是角度误差。在较小的速度梯度下,七孔探针可以满足精度要求。随着圆管中心向管壁处速度剪切程度逐渐增大,测量的系统误差也随之增大。实验结果表明,速度梯度小于等于0.10(m/s)/mm的剪切流场,直径6mm 的七孔探针可以满足测量要求。

表5 实验误差分析Table 5 Error analysis of the experiment
5 结 论
(1)有限直径的七孔探针在测量剪切流场中,由于空间分辨率有限,会引入系统误差。流场速度梯度越大,探针直径越大,则误差越大。
(2)七孔探针测量的主要误差是角度误差。计算和实验结果均显示,在相同条件下,随着流场速度梯度的增加,相比速度误差而言,角度误差首先超出精度允许的范围,即角度测量对剪切流场的敏感性更大。
(3)本文定义 “临界直径D”,为测量中满足精度要求的最大探针直径。在测量某一速度梯度的剪切流场中,必须选用小于等于“临界直径D”的七孔探针,才能保证测量精度。本文绘制了误差随速度梯度和探针直径变化的曲面示意图,用以选择合适尺寸的七孔探针。
[1]ZILLIAC G G.Modeling,calibration,and error analysis of seven-hole pressure probes[J].Experimentsin Fluids,1993,14:104-120.
[2]GERNER A A,MAURER C L,GALLINGTON R W.Non-nulling seven-hole probes on high angle flow measurement[J].ExperimentsinFluids,1984,2:95-103.
[3]PAYNE F M,NG T T,NELSON R C.Seven-hole probe measurement of leading edge vortex flows[J].ExperimentsinFluids,1989,7:1-8.
[4]SUMMER D,HESELTINE J L,DANSEREAU O J P.Wake structure of a finite circular cylinder of small aspect retio[J].ExperimentsinFluids,2004:720-730.
[5]顾蕴松等.翼尖涡流场特性及其控制[J].空气动力学学报,2008,26(4):446-451.
[6]余莉,明晓,陈丽君.不同透气情况降落伞的流场试验研究[J].空气动力学学报,2008,26(1):20-25.
[7]H.史里希廷.边界层理论(下)[M].科学出版社,1991,1:839-842.

