基于非定常涡格法的扑翼飞行器气动特性优化

贺红林，周 翔，朱保利，余春锦

（南昌航空大学 航空制造工程学院，江西 南昌330063）

0 引 言

扑翼飞行器（FMAV）集举升、悬停、推进功能于其机翼，具有尺寸小、质量轻、机动性好、效率高等特点，在军事与民用上具有广泛的应用前景。因其在气动与稳定性等方面存在明显优势，FMAV已成为微型飞行器的研究热点。近些年，适于高性能FMAV研制的需要，对其气动问题进行了不少研究，如Smith［1］和 Vest［2］采用面元法研究了飞鸟气动特性；Sun［3］通过对N－S方程的数值求解并基于涡动力学理论阐释了扑翼的非定常气动特性；Joseph［4］采用非定常涡格法（UVLM）模拟柔性扑翼流场；Lin用MOC法求解Euler／Navier－Stokes方程以模拟扑翼运动［5］。在这些方法中，面元法简单但计算结果较粗糙；CFD法的结果较准确，但计算开销巨大，只适于刚性扑翼［6］；UVLM快速高效且可对流－构耦合态的柔性扑翼上的涡分布、尾涡变化等多种因素进行建模计算，并能获得较准确气动结果［7］。总的来看，已有的研究主要集中于扑翼流场的模拟，对于扑翼的选型和设计支持不够。事实上，实用中更关注的是扑翼结构及其扑动参数确定问题。据此，旨在为扑翼选型与设计提供一定依据，本文探索FMAV的气动优化，并将在对FMAV进行气动分析及其UVLM建模的基础上，引入GPU（Graphic Processing Unit）技术实现该算法，以满足 优化迭代中海量计算的需要，同时，考虑到UVLM模型不能提供导数信息，还将引入模式搜索（PS）法作为FMAV的寻优工具。

1 非定常涡格法建模

1.1 翼面速度表示

为了表征扑翼的运动，在其上定义惯性坐标系O（X，Y，Z）和机翼坐标系o（x，y，z），前者固定不动，后者随机翼运动，并设两者在初始时刻位置重合。若在t（＞0）时刻，机翼坐标系在惯性系中位姿为R0＝（X0，Y0，Z0），D0＝（α，β，γ），则机翼系内的翼面任意点A（x，y，z）在惯性系内的速度

1.2 扑翼流场边界条件

机翼扑动时，除前缘及翼尾的部分区域外，其它各处流场为不可压无旋流，为此定义速度势函数Φ（X，Y，Z）并满足：▽2Φ＝0。因扑翼对远处流场影响很小，因此其远场边界条件为Φ＝0。而近场边界条件则满足无穿透条件，即

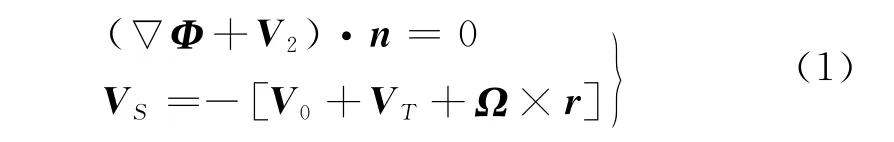
式中，VS为翼面相对运动速度，V0为来流速度，VT、Ω分别为翼面平动和转动速度，n为翼面单位法矢。

1.3 尾涡模型

扑翼的气动状态主要取决其尾涡。根据Kelven定律，当扑翼运行时其流场环量之和恒为常数。这意味着流场总环量的任何变化都会在尾流区引起等值、符号相反的涡量变化。该变化将发展成翼后缘沿角平分线处发散出的一段涡线。当翼面环量随翼扑动而变化时，翼后缘将拖出一列连续涡带。可按间距V（t）Δt对涡带进行离散，且只需选取适当的时间间隔Δt，就可用一组离散尾涡环模拟该涡带。各离散涡环量应等于相应时段从翼后缘所脱离涡带之涡强的积分，即

这样，便得到图1所示扑翼UVLM模型。若第i时段内，环量Γ（t）的变化ΔΓi（t）＝Γi＋1（t）－Γi（t），则根据Kelven定律，从翼后缘脱离出的离散尾涡环量ΓWAKEi＝－ΔΓi（t）。为了确定该涡环位置，可假定在一定区域内其涡强不变且不耗散。若用虚线表示第i时段内翼后缘的运动轨迹，如图2所示，则离散涡ΓWAKEi应位于该虚线上。需指出的是，确定涡环位置时，应避免将其涡心置于机翼后缘上，否则该涡的诱导速度将成为无穷大。本文将涡心定位于距翼后缘0.25V（t）Δt的位置。

图1 尾涡离散示意图Fig.1 Schematic of discretization of the wake vortex

当前时段前生成的离散涡均以当地气流速度VWAKEI运动，可通过对机翼及整个尾迹区在该点的诱导速度进行叠加求得。若设离散涡在第i时段相对于前一时段的位移ΔSi＝VWAKEiΔt，则其下一时刻涡环的位置为

依据上式可递推出各离散尾涡的当前时刻位置，进而可得到各尾涡的运行状态。

图2 新生成尾涡的位置Fig.2 The position of the new wake vortex

1.4 FMAV 载荷计算

扑翼的周边流场用非定常伯努力方程描述［6］

式中，pref为距翼面无穷远处的压强。与定常伯努力方程相比，上式的不同在于它增加了势函数偏微项∂Φ／∂t。FMAV的承载能力隐含在压强p之中并可通过数值解法求得。

1.5 UVLM数值求解

计算FMAV的气动特性时，需先对它进行网格化，其方法与定常涡格法相似［8］，只是因FMAV的翼面形状不断变化，因此在各计算周期内需对网格重新进行划分。为此，定义翼弦向为i向，展向为j向，并将翼面划分为M×N＝m个面元，且为各面元配置一个四边形涡环。涡环前缘位于面元1／4弦线处，并取面元3／4弦线的中点为控制点，该点处气流速度满足式（1）。设面元两对角线向量为A和B，则其单位法矢为

涡环环量方向由右手法则确定。这样，利用m个涡环可模拟机翼对流场之作用。涡环（i，j）在任意位置产生的诱导速度为涡环四条边共同诱导的结果，它可由B－S定律确定，即

dv为微量涡线段dl的诱导速度，r为涡线段至诱导点距离向量。通过对涡环上各涡线的诱导作用进行叠加，可确定涡环对指定点的诱导速度。面元的控制点处气流速度是由翼面运动产生的相对气流速度（u′，v′，w′）K、面元涡诱导速度、尾流诱导速度（uw，vw，ww）K构成。设第1面元单位强度涡环在第k面元控制点的诱导速度为（u，v，w），并引入气动影响系数ak1表示其诱导作用，即

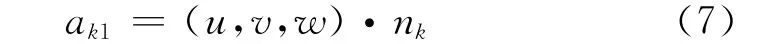
类似地，将其余面元的影响系数依次表示为aK2，…，akm。依据式（1），可将第 面元的无穿透边界条件可完成

将上式中的已知项移至等号右侧，可得

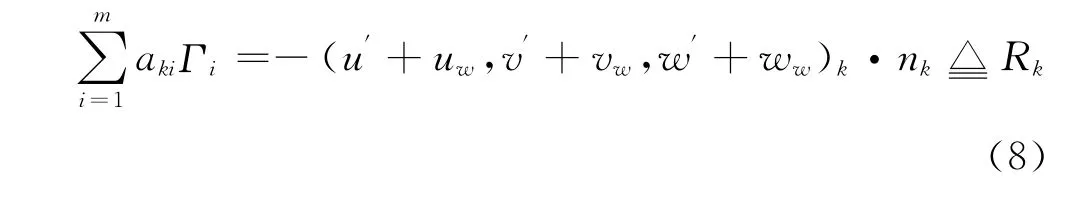
上式写成矩阵方程形式，有

求解上式可得各面元涡量。再通过对式（4）进行差分处理，就可得到面元（i，j）的压差

式中，τi、τj分别为面元弦向和展向切矢，Δcij和Δbij是面元弦向和展向宽度。通过叠加各面元压差即可求得机翼的气动力，即

F的垂直和水平分量即为扑翼升力和推力。

2 面向对象的ULVM实现

对于给定翼面，可将其离散成一系列四边形涡环，各涡环又可分解为四条涡线段。将此分解思路进行抽象，便得到UVLM面向对象的实现构架。为此，可先构建涡线段类以保存涡线段有关信息及其诱导速度算法；再使用该类构建涡环类，涡环类包含四个涡线段子类，保存面元法向量及控制点等信息；基于涡环类构建涡环网格类，网络类将涡环按照给定的几何参数组织成网格以描述翼面和尾迹，利用该类可派生出翼面类和尾迹类。最后，使用上述基本类构建机翼运动、线性方程求解、气动力计算和输出结果数据的辅助类及控制时间步进迭代类。这样就可编写出UVLM程序，图3给出了程序框架。需要指出的是，因尾迹涡环量的更新计算量巨大，而该运算又特别适于并行处理，为提高算法效率，本文引入GPU求解器并利用其并行计算能力实现尾涡求解［10］，从而使ULVM求解速度达到CPU求解时的3倍。这不仅提高求解速度，更重要的是它使UVLM可作为FMAV优化迭代的气动计算工具。

图3 UVLM的面向对象程序框架Fig.3 The object oriented program framework for UVLM

3 模式搜索法寻优

3.1 优化方法确定

FWAV的气动优化基于UVLM的海量气动计算。由于UVLM是一种不依赖于解析目标函数的离散数值法且它不提供导数信息，因此，该方法不适于需对目标函数进行求导的优化场合（如牛顿迭代法）。众所周知，PS法是一种直接搜索法，无需解析性目标函数且寻优效率较高，因此，本文的扑翼优化即选定它作为FMAV的气动寻优工具。

3.2 PS法的实现

式中，B∈Rn×n为基矩阵，在各迭代步中保持不变；Ck∈Zn×p为生成矩阵，形如

其中，Mk∈Zn×n和Lk∈Zn×（p－2n）中至少包含一列零向量。搜索方向即取Pk的某一列。

对于给定搜索步长Δk＞0，定义探测向量

式中，为Ck的第i列。第k步迭代时，需从，…中寻找满足如下条件的，即

若 min｛f（xk＋y），y∈Δk［BMk－BMkBLk］｝＜f（xk），则f（xk＋）＜f（xk），可取xk＋1＝xk＋。

在2n个搜索方向中只要有一个能使f（x）下降，则搜索步长与该列相乘得到的就将使目标函数值下降。依据此思路且通过多次优化迭代，就可寻得上述问题的最优解。根据上述理论，编写了模式搜索法程序模块，并将UVLM嵌入到该优化程序，从而实现了FMAV气动计算与寻优的整合。经整合后的程序具备了FMAV气动优化能力。

4 气动特性优化

4.1 扑动模型

本文选定柔性扑翼作为优化对象。根据FMAV运动特点，翼面扑动时其柔性变形主要发生在机翼的弦向，因此优化所针对的扑动模型只考虑翼的弦向的柔性，并假定其为

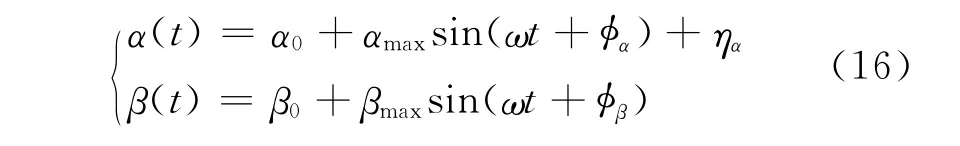
式中，ηα是用于描述柔性形变的弦向扭转角，它随翼面形变沿展向和弦向增大，形如

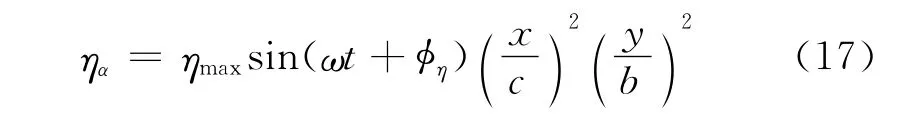
式中，ηmax为最大扭转角，φη为扭转形变翼面扑动间的相位差，x和y分别为翼面坐标，c、b分别是翼的弦长和展长。

4.2 扑动相角优化

为验证上述优化方法的有效性，首先研究了FMAV的一维气动优化。众所周知，鸟飞时，翅翼不仅要上扑还需下扑，并且扑动时还存在绕前缘的俯仰角变化，即其扑翅和俯仰间存在相位差Δφ＝φα－φβ。根据鸟扑动产生时气动力的机理，易知该相位差对于鸟的气动特别是其升力有很大影响。这就给我们一个启示，要改善柔性扑翼的气动条件，必须对其扑动与俯仰间的同步关系进行合理规划。基于这种认识，选取某矩形直机翼进行优化，该翼的展弦比为8，攻角为5°，最大扑动角αmax＝5°，βmax＝15°，减缩频率k＝0.1。优化时，以平均升力系数的最大化为优化目标，以扑动－俯仰相位差为优化变量，并沿翼面展向和弦向划分16×6个面元，不考虑弦向柔性，只考虑扑动角和机翼绕前缘俯仰角变化并假定俯仰角沿翼展方向逐渐增大，优化模型为

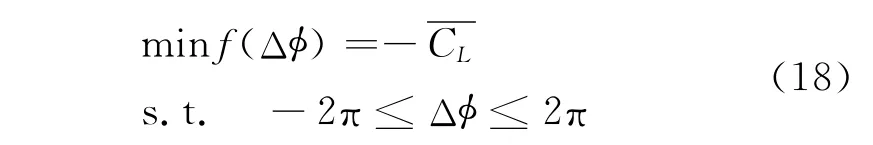
用PS法求式（18）时，初始搜索点取为零点，初始步长设定为0.5，图4给出了优化搜索轨迹，PS法经14次迭代后收敛于Δφ＝－1.227rad，即当扑动－俯仰相位差Δφ＝289.76°时，扑翼将获得最大平均升力系数。该结果与文献［11］中以15°为步长逐渐增大Δφ算得的平均升力变化曲线非常吻合，表明要使FMAV获得尽可能大的升力系数，其扑动与俯仰运动的相位差有一个最佳值。它同时也表明，内嵌了通过GPU实现UVLM的模式搜索法能有效地实现FMAV优化。

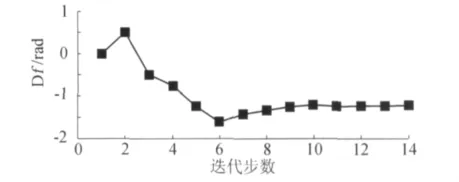
图4 模式搜索迭代轨迹Fig.4 Optimization of the phase difference between the flapping and pitching using Pattern－Search Method

4.3 翼型结构优化

根据飞行器多学科优化中的外形参数化设计思想，本文在矩直翼基础上，进行了机翼气动布局优化计算。给定矩直翼参数为：翼展b＝0.6m，翼根与翼稍弦长均为c＝0.1m，翼面积S＝0.06m2。优化条件是在保持翼面积不变前提下，将翼根和翼梢弦长减小，而在某一展向相对位置p∈［0，1］处将机翼的弦长增大为cmax∈［1.0，1.5］，如图5所示。为了保证机翼面积不变，cmax与翼根弦长croot满足关系

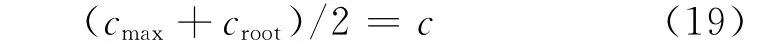
图5 参数化外形优化结果Fig.5 Optimal flapping wing shapes

优化建模时，以式（17）为扑动模型，取αmax＝10°，βmax＝30°，减缩频率ζ＝0.2，不考虑柔性形变引起的扭转角，并分别以平均推力系数和平均升力系数为目标函数，以p和cmax作为设计变量。这样，便得到扑翼的优化模型

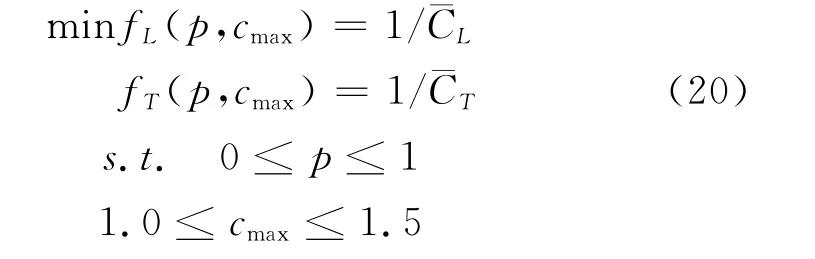
求解式（20）时，需先采用惩罚函数法将其转为无约束优化问题，再调用PS模块进行优化迭代，通过在迭代中进行大量UVLM计算寻找最佳气动参数。图6给出了迭代过程及其气动状态。表1给出了优化结果。据此得到图5所示两种优化翼形。可见，要提高平均推力，翼面宜呈倒梯形布局，且应使外翼段具有较大面积；反之，要想升力最大化，应使内翼段面积取较大值。造成两种翼形差异较大的原因，主要是因为翼在扑动过程中，其内翼段与外翼段会形成几何扭转，而且当下扑时，外翼段的扭转使翼产生的合力在向前方向上有一个分量，该分量将形成推力和升力，但内翼段却主要产生升力，当翼面呈倒梯形时，其翼尖处的运动速度较快，造成翼刚度小、柔性形变大，因而可形成较大推力。但若翼采用正梯形布局，则内翼段面积会增大，故可获得较大升力。上述结果也意味着对于给定翼型，可能无法使其升力和推力同时最大化，它表明在翼面设计过程中需综合多种因素进行权衡。

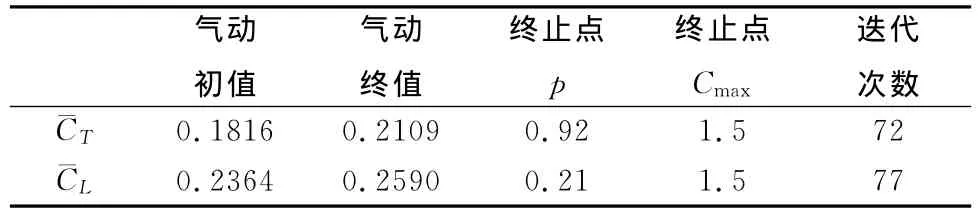
表1 气动力优化结果Table 1 Results of aerodynamic optimiation

4.4 扑动参数优化

扑动参数优化并非什么新问题，但此方面已有的研究主要针对单个参数的优化。实际上，如同鸟飞时需同时协调好多个扑动参数一样，要想FMAV产生理想的气动状态，同样需考虑多个扑动参数的共同影响。为此，本文选取NACA0012矩直翼（展长为0.8，展弦比A＝8）为对象，以平均推力系数最大化为优化目标，同时对扑动频率与柔性扭转角进行了优化。根据扑翼飞行的实情，假定扑动频率f∈［4Hz，10Hz］，弦向扭转角φη∈［10°，45°］，来流速度Vo＝5m／s，扑动角βmax＝40°，俯仰角αmax＝0°，将翼面划分为16×4个面元。这样，其优化问题描述为

表2列出了扑翼的多参数优化结果。可见，使平均推力系数最大的扑动频率为频率范围内的最大值，而柔性形变扭转角为24.85°。根据文献［11］，当扑动频率固定为6Hz而不断增大扭转角时，将在扭转角φη＝30°处使平均推力达到最大值。但由本文的优化结果可知，随着扑动频率增加，对应于最大推力系数的扭转角将发生一定的变化，并且随着频率增加，最大值扭转角应相应地减小，即翼面柔性呈降低趋势才能保证在该扑动频率下的推力最大。

表2 扑动频率与弦向扭转角优化结果Table 2 Optimiation of twist angle and the flapping frequency

5 结 论

（1）基于UVLM并通过GPU实现其气动计算的模式搜索优化法，运算速度快、计算精度高，可望成为FMAV气动优化的重要工具。

（2）为提高FMAV的升力，应使扑翼的扑动与俯仰运动间存在一定相位差，并且当相位差接近289.76°时，其升力达到峰值。

（3）为实现FMAV推力最大化，应在增大扑动频率时适度地减小机翼的柔性扭转角。

（4）要使FMAV产生较大气动推力，其翼面宜呈倒梯形结构；反之，要获得大的推力，翼面结构宜呈梯形布局。

［1］SMITH M J C，WILKIN P J，WILLIAMS M H.The advantages of an unsteady panel method in modeling the aerodynamic forces on a rigid flapping wing［J］.J.Exp.Biol.，1996，199：1073－1083.

［2］VEST M S，KATZ J.Unsteady aerodynamic model of flapping wings［J］.AIAAJournal，1996，34（5）：1435－1440.

［3］SUN M，TANG J.Aerodynamic force generation and power requirements in forward flight in a fruit fly with modeled wing motion［J］.J.Exp.Biol.，2003，206（12）：3065－3083.

［4］JOSEPH K，ALLEN P.Low speed aerodynamics：from wing theory to panel method［M］.New York：McGraw －Hill Book Co.1991.

［5］LIN S Y，HU J J.Aerodynamics performance study of flapping－wing flow fields［C］.23rd AIAA Applied Aerodynamics Conference 6－9June 2005：4123－1427.

［6］曾锐.仿鸟微型扑翼飞行器的气动特性研究［D］.［博士学位论文］.南京：南京航空航天大学，2005.

［7］FRITZ，LONG L N.Object－oriented unsteady vortex lattice method for flapping flight［J］.JournalofAircraft，2004，41（6）：1275－1290.

［8］DANIEL T L，COMBES S A.Flexing wings and fins：bending by inertial or fluid－dynamic forces［J］.IntegrativeComparativeBiology，2002，42（10）：1044－1049.

［9］肖天航，昂海松.大幅运动复杂构形扑翼动态网格生成的一种新方法［J］.航空学报，2008，29（1）：41－48.

［10］LEWIS R M，TORCZON V.Pattern search method for bound constrained minimization［J］.JournalonOptimization，1999，28（4）：1365－1372.

［11］曾锐，昂海松.扑翼柔性及其对气动特性的影响［J］.计算力学学报.2005，26（6）：750－754.