蜂窝夹芯板表面加工的平整度分析

夏盛来，何景武，王耀东

（北京航空航天大学航空科学与工程学院，北京100191）

蜂窝夹芯板表面加工的平整度分析

夏盛来，何景武，王耀东

（北京航空航天大学航空科学与工程学院，北京100191）

蜂窝夹芯结构具有高的比强度、比刚度以及质量轻等优点，被广泛应用于航空航天领域。因此，对其进行力学特性分析具有理论研究和工程应用价值。针对卫星常用的蜂窝夹芯结构板，实验测得夹芯板的表面平整度。根据理论推导得出蜂窝夹芯结构的等效材料参数，利用有限元分析软件MSC.Patran/Nastran进行蜂窝夹芯板的表面平整度分析。对比发现，实验结果和计算分析结果相差为5.9%，表明理论推导的可行性。根据三明治等效理论，提出建立常用规格的蜂窝的等效参数的等效系数库，便于蜂窝夹芯结构的工程应用。

蜂窝夹芯板；等效模型；等效参数

蜂窝夹芯板结构以其比强度高、比刚度高、隔热隔振性能好、可设计性强等特点被广泛应用于航空航天领域，尤其是在现代卫星结构中，蜂窝夹芯结构已成为主要的承力结构［1］。铝蜂窝夹芯板因其轻质、不易变形，成为蜂窝夹芯板中应用比较多的一种结构［2］。因此，对其进行研究，具有很高的工程实用价值。

蜂窝夹芯板的力学性能通过做实验得到比较准确可靠的信息。但是做实验存在以下缺点：实验花费比较大；实验结果具有离散性；实验结果具有针对性，缺乏通用性。因此在实验的基础上有必要进行理论分析。理论分析可以克服实验的种种缺点，二者结合起来，以实验检验理论分析，以理论分析来指导实验，可以真实可信的掌握蜂窝夹芯这类结构的力学特性。

通常，采用有限元法进行结构的力学特性分析，目前市场上比较流行的有限元分析软件已经非常成熟。对结构进行有限元分析时，需要建立有限元模型，填写结构的材料属性。针对蜂窝夹芯结构，建立真实的有限元模型比较困难［3］，模型规模较大，需要占据较大的计算存储空间和计算时间。因此可以采取模型等效法以等效模型代替真实模型，这就需要将结构的材料属性进行相应的参数等效。这也是研究蜂窝夹芯结构常用的理论分析方法。

本工作研究的铝蜂窝夹芯板是某卫星结构中比较关键的功能板，其面板和底板采用铝合金板，蜂窝夹芯采用铝材。因为正六边形夹芯形式具有省料、易于制造、结构高效等特点［4］，因此这种形式夹芯被广泛采用。本工作针对这种夹芯形式的蜂窝夹芯板进行了实验和理论推导研究。首先针对铝蜂窝夹芯板进行了实验，测量出其面板的表面平整度，然后根据等效理论［5］推导出等效参数，通过有限元法分析了蜂窝夹芯板的表面平整度。

1 实验

1.1 铝蜂窝夹芯板简介

铝蜂窝夹芯板结构图见图1。蜂窝夹芯板中间埋有4块电缆保护盒。蜂窝夹芯板的长宽高外形尺寸700mm×350mm×25.6mm，上下面板为厚度0.4mm的LY12CZ铝合金。蜂窝芯选用国产有孔铝蜂窝芯，规格为LF2－Y 0.03/5（GB3614—82），即为正六边形铝合金蜂窝，蜂窝壁板边长为5mm，蜂窝壁板厚度为0.03mm。面板与蜂窝夹芯采用J－78B胶膜连接，胶膜厚度为0.3mm，材料为环氧树脂胶黏剂，胶膜在70～80℃温度条件下，流动性最好，在130℃温度条件下固化。电缆保护盒尺寸为1.4mm×26mm材料为铝合金，主要用于保护蜂窝夹芯结构中电缆使其不受压。铝蜂窝夹芯板结构示意图见图2。整个蜂窝夹芯板中在宽度方向上共有4组保护盒。截面示意图见图3。

图3 铝蜂窝夹芯板截面示意图Fig.3 Sectional sketch map of aluminum honeycomb sandwich panel

1.2 实验过程

铝蜂窝夹芯板放置于实验平台上，埋置电缆保护盒一侧面板紧贴模具；在夹芯板四周放置质量较大的挡条，防止蜂窝结构板在平面内产生较大位移；用真空袋罩住挡条和蜂窝夹芯板，袋内抽真空，袋外充气，施加温度载荷。压力载荷和温度载荷具体施加情况见《固化规范》，表1为固化规范。实验检测环境为标准大气压，检测温度为室温（20°）。

表1 固化规范Table 1 Solidification criterion

1.3 实验结果

实验过程中测量了铝蜂窝夹芯板的上面板的表面平整度，即测量了其上面板法向变形。用于实验的铝蜂窝夹芯板见图4。由于共有4组电缆保护盒，沿铝蜂窝夹芯板长度方向上在50，130，200，270，450，650mm处布置了测点，平整度数值单位为mm，测量结果见表2。

图4 铝蜂窝夹芯板结构实验件Fig.4 Testing structure of aluminum honeycomb sandwich panel

2 理论分析

随着蜂窝夹芯板结构的广泛应用，其力学特性的研究显得愈发重要。在进行蜂窝夹芯结构的力学特性分析时，通常采用有限元素法。这方面有多种成熟的有限元分析软件，如MSC.Patran/Nastran或Ansys等，但由于这些程序中没有专门模拟蜂窝结构的单元，因此分析计算时，处理蜂窝夹芯结构一般采用两种方法，一是通过薄板单元真实模拟蜂窝壁板，一是通过等效参数法等效处理蜂窝夹芯结构参数。由于真实模拟计算网格规模比较大，因此普遍的处理方法是采用等效参数法。

表2 铝蜂窝夹芯板表面平整度Table 2 Surface smoothness of aluminum honeycomb sandwich panel

蜂窝夹芯结构的等效参数法主要包括3种，即三明治理论、蜂窝板理论、等效板理论。

2.1 三明治理论

三明治理论是对蜂窝夹芯进行等效，上下面板采用面板本身的材料参数。三明治夹芯板理论是对蜂窝夹芯进行等效的一种有效方法，假定芯层能抵抗横向剪切变形并且具有一定的面内刚度，上、下蒙皮层服从Kirchhoff假设，忽略其抵抗横向剪应力的能力，则蜂窝芯层可以等效为一均质的厚度不变的正交异性层。示意图如图5所示。

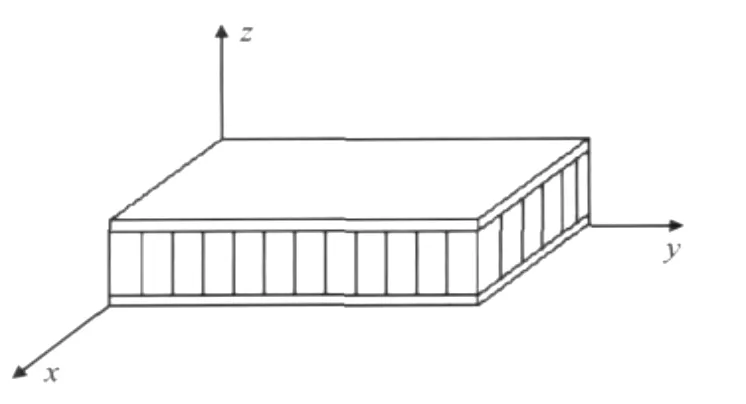
图6 蜂窝板示意图Fig.6 Sketch map of honeycomb sandwich panel

蜂窝夹芯结构的等效研究从20世纪50年代末已经开始研究，到20世纪80年代初Gibson［6］等推导出等效的材料常数Ex，Ey，Gxy，Vxy，Vyx，但推导过程没有考虑蜂窝夹芯胞壁的伸缩变形；富明慧［7］将胞壁的伸缩变形考虑到等效推导过程中，但节点力不满足平衡条件；王颖坚［8］引入弯矩，建立剪力作用下的等效模式，但不满足整个蜂窝芯子的结构的力的平衡；赵金森［9］在Gibson推导的基础上对Gibson推导公式进行了修正，推导出一系列新的等效参数公式，推导结果如下：

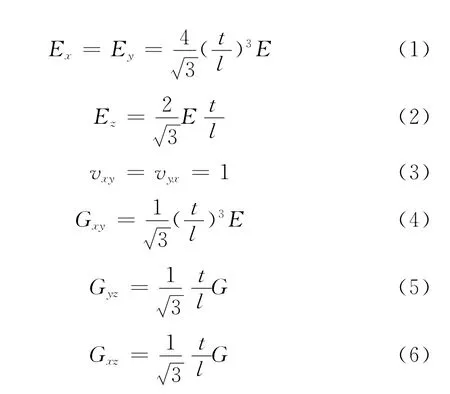
在这里，研究的是正六边形蜂窝，式中：t代表蜂窝的壁厚；l代表蜂窝的边距。

2.2 蜂窝板理论

蜂窝板理论是将整个蜂窝夹芯板等效成等刚度、同尺寸的正交各向异性板，同时考虑了表层和夹芯的面内和面外力学性质，推导出等效力学模型的等效弹性参数，为通用有限元程序提供必要的输入参数。夏利娟［2］、徐胜今［1］在文献中给出了等效推导过程及计算公式，推导结果如下：

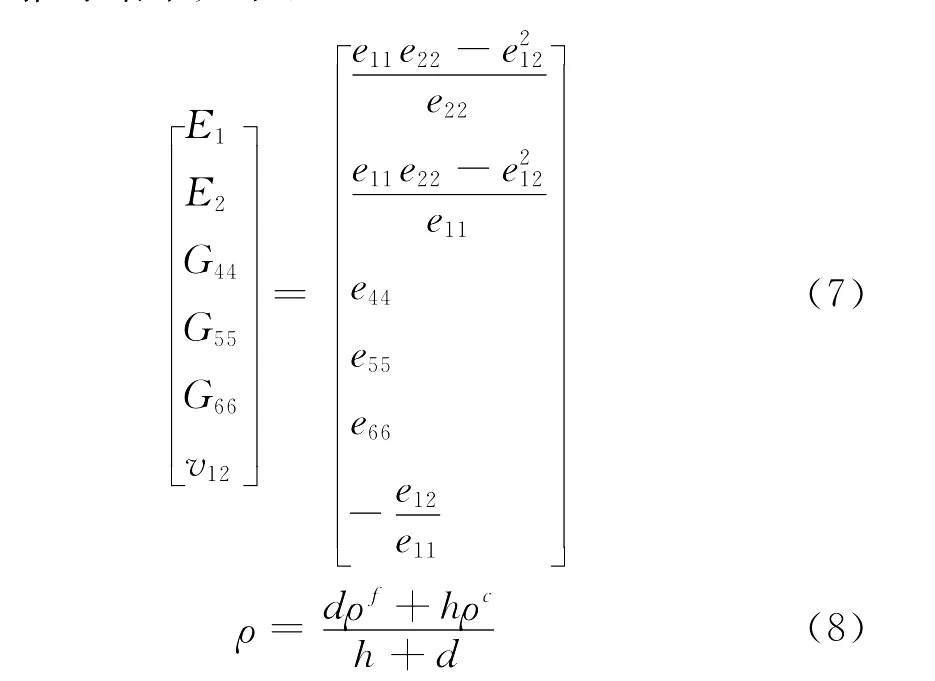
式（7）中，eij（i＝1～6，j＝1～6）有如下关系，

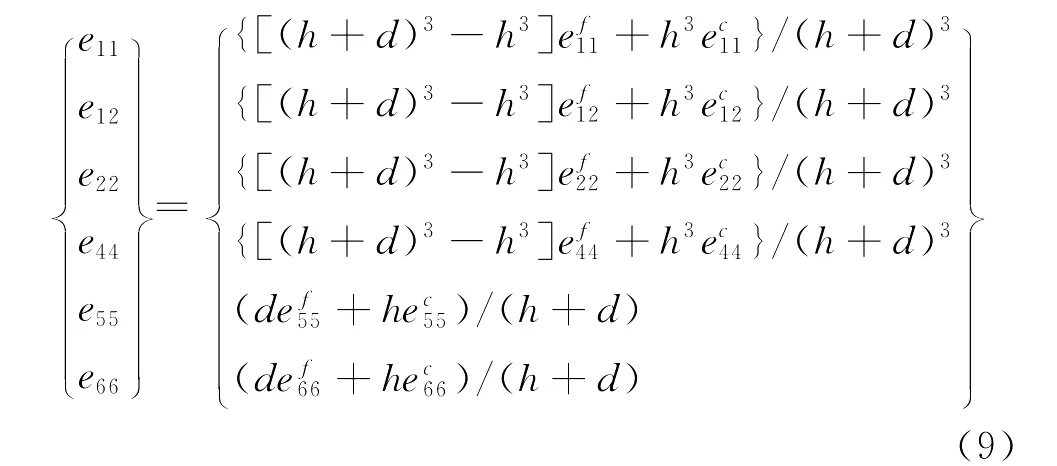
式中：2h为蜂窝的高度；d为铝板的厚度；efij为铝板的刚度系数；ecij为蜂窝夹芯结构的刚度系数；ρf为铝板的密度；ρc为蜂窝夹芯结构的密度。

2.3 等效板理论

等效板理论就是将蜂窝夹芯板等效成与原夹芯板不等厚度的各向同性的壳元素。所谓壳元素就是它不但像弯曲板一样承受垂直板面的剪力载荷和弯扭载荷，还能像平面应力板一样承受面内的拉压和剪切载荷。其中，作为弯曲板，符合小挠度薄板的Kirchhoff假设。程改霞［10］，夏利娟［2］在文献中给出了推导过程及计算公式，推导结果如下：

式中：2 H为蜂窝夹层板总厚度；d为铝板厚度；ρf为铝板的密度；ρc为蜂窝夹芯结构的密度。

理论上说，三种等效理论推导原理各有不同，具体选择哪种等效理论需要根据具体情况而定。由于研究中的蜂窝夹芯结构还与其他的外围结构相连，因此采用等效板理论改变了结构的厚度，在有限元分析时结构之间的连接存在问题，因此适宜采用三明治等效理论和蜂窝板等效理论。

3 结果对比分析

本研究采用三明治等效理论对蜂窝夹芯板进行有限元分析。实验用铝蜂窝夹芯板的材料属性参数如下：E＝72GPa，v＝0.3，G＝27GPa，ρ＝2.7g/cm3。根据三明治等效理论推导得到蜂窝夹芯结构的等效参数为：

根据三明治等效原理利用MSC.Patran/Nastran软件建立了有限元模型，载荷及约束情况与实验过程相对应，材料参数为理论推导的等效参数，有限元计算云图如图6所示，从计算结果看，蜂窝夹芯板的最大变形为0.941mm。

4 讨论

图6 蜂窝夹芯板变形云图Fig.6 Deformation spectrum of honeycomb sandwich panel

蜂窝夹芯板的实验结果可见，1～4＃的保护盒上蒙皮变形数值比较分散，其中1＃和4＃保护盒的数值分散程度比较严重，这与1＃和4＃保护盒处于边缘有一定的关系，而且，实验件在生产过程中每个区域也会存在差异，在此处取2＃和3＃保护盒的平均值来衡量蜂窝夹芯板的表面平整度。实验平均值为1.035mm。假如进一步消除2＃和3＃保护盒边缘的影响，实验平均值为1mm。

有限元分析计算得到的保护盒表面平整度为0.941mm。比较实验结果和有限元分析结果发现，实验值比有限元分析值大0.094mm，二者相差9%。消除2＃和3＃保护盒边缘的影响，则误差为5.9%。说明三明治等效理论计算的理论值能够满足要求。

从三明治等效理论推导的结果来看，公式（1）～（6）中，材料的等效参数与原材料参数之间的系数为蜂窝壁厚及边距的函数。即可将式（1）～（6）表示成式（18）～（20）式。

即有

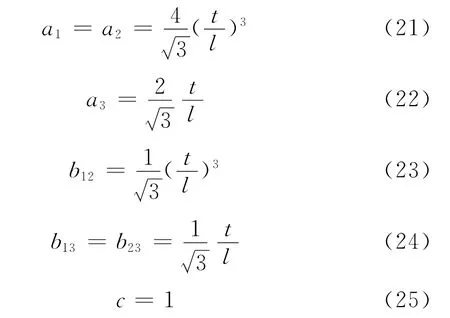
在蜂窝的边距l、壁厚t一定的情况下，则系数a，b，c为常数。即系数a，b，c与材料类型无关，仅与蜂窝的规格相关。这就保证了等效理论的通用性。因此针对蜂窝夹芯结构，根据不同的规格，可以建立一个蜂窝夹芯结构等效系数库，便于蜂窝夹芯这类结构的等效处理。而且可以明显减少实验的次数，便于蜂窝夹芯结构的工程应用。

根据系数函数式（21）～（25），可以计算出蜂窝结构的等效参数。在这里给出几组常用规格的蜂窝夹芯结构的等效系数，见表3。

表3 不同规格蜂窝等效系数表Table 3 Equivalent coefficient database of different specification honeycomb panel

5 结论

（1）比较实验和理论计算结果发现，蜂窝夹芯板的表面平整度相差在5.9%～9%之间，说明理论推导的结果是可信的。

（2）比较三种等效理论，等效板理论最简单，但不能体现蜂窝夹芯的信息，比较适合快速估算；三明治理论比较直观，容易实现；而蜂窝板理论推导过程比较复杂，且推导过程需要用到三明治理论的结果。

（3）分析三明治等效理论发现，等效参数的等效系数与材料无关，仅与蜂窝夹芯规格相关，因此具有通用性，可以将常用规格的蜂窝建立等效系数库，便于蜂窝夹芯结构在工程应用中快速查找。

（4）对等效系数研究发现，在蜂窝壁厚与边距比例不变时，等效系数相同，这一点还需要通过实验来验证。假如这一结果成立，对于蜂窝结构的修改、设计具有指导作用。

（5）通过快速的分析计算，可以为蜂窝板的加工制造提供指导意见，可以快速地选择蜂窝的型号，而且在生产前就能基本了解蜂窝结构板的力学特征。

［1］ 徐胜今，孔宪仁，王本利，等.正交异性蜂窝夹层板动、静力学问题的等效分析［J］.复合材料学报，2000，17（3）：92－95.

［2］ 刘叶花，谢桂兰，曹尉南，等.铝蜂窝胞元结构对其宏观等效表征性能的影响［J］.材料工程，2011，（11）：29－34.

［3］ 冯春燕，于大永.蜂窝梁扰度计算方法研究［J］.四川建筑科学研究，2012，38（1）：65－69.

［4］ 夏利捐，金咸定，汪庠宝.卫星结构蜂窝夹层板的等效计算［J］.上海交通大学学报，2003，37（7）：999－1001.

［5］ 张铁亮，丁运亮，金海波.蜂窝夹层板结构等效模型比较分析［J］.应用力学学报，2011，28（3）：275－282.

［6］ GIBSON L J，ASHBY M F，SCHAJER G S.The mechanics of two－dimensional cellular materials［J］.Proc R Soc A，1982，382（1782）：25－42.

［7］ 富明慧，尹久仁.蜂窝芯层的等效弹性参数［J］.力学学报，1999，31（1）：113－118.

［8］ 王颖坚.蜂窝结构在面内剪力作用下的变形模式［J］.北京大学学报，1991，27（3）：302－306.

［9］ 赵金森.铝蜂窝夹层板的力学性能等效模型研究［D］.南京：南京航空航天大学，2006.7－25.

［10］ 程改霞，郑晓亚，张铎，等.蜂窝夹层结构，等效板力学特性研究［J］.弹箭与制导学报，2004，24（5）：568－570.

Surface Artifactitious Smoothness Analysis of Honeycomb Sandwich Panel

XIA Sheng－lai，HE Jing－wu，WANG Yao－dong
（School of Aeronautic Science and Engineering，Beihang University，Beijing 100191，China）

Honeycomb sandwich structure with high specific strength，stiffness and light weight，etc.，are widely used in aerospace applications.Therefore，analysis of its mechanical properties has a great value in theoretical research and engineering application.Using the honeycomb sandwich panels that are commonly used for the satellite structure，sandwich panel test measured the surface roughness.According to theory，this paper deduced the equivalent material parameters of honeycomb sandwich structure，and also analyzed the panel surface roughness with finite element software MSC.Patran/Nastran.Comparison between the test results and calculate results with the difference of 5.9%，indicate the feasibility of theoretical derivation.According to the equivalent sandwich theory，proposed the establishment of the equivalent coefficient database about the cellular equivalent parameters which was the common specifications，facilitating the engineering applications of honeycomb sandwich structure.

honeycomb sandwich panel；equivalent model；equivalent parameter

V45

A

1001－4381（2012）06－0043－05

2011－12－02；

2012－04－05

夏盛来（1977－），男，博士生，主要研究飞行器结构设计，结构强度分析及结构动力学，联系地址：北京市海淀区学院路37号北京航空航天大学航空科学与工程学院飞机所（100191），E－mail：xiashenglai＠ase.buaa.edu.cn