钨合金动态力学性能的三维数值模拟研究

刘海燕，宋卫东，栗建桥

（1北京理工大学宇航学院，北京100081；2北京理工大学爆炸科学与技术国家重点实验室，北京100081）

钨合金动态力学性能的三维数值模拟研究

刘海燕1，宋卫东2，栗建桥2

（1北京理工大学宇航学院，北京100081；2北京理工大学爆炸科学与技术国家重点实验室，北京100081）

采用数值模拟的方法对钨合金在冲击载荷作用下的动态力学响应进行了研究。运用有限元动力分析程序建立了具有典型微观结构钨合金三维有限元单胞模型，对钨合金在拉伸载荷作用下的动态力学性能进行了数值模拟研究，分析了应变率对其力学性能的影响，给出了不同应变率条件下单胞模型的应力和应变分布云图，在与实验结果对比的基础上验证了该有限元模型的可靠性。

钨合金；动态力学性能；微观结构；数值模拟

钨基高密度合金是一类以钨为基体（含钨量为85%～99%），并添加有少量的Ni，Cu，Fe，Co，Mo，Cr等元素组成的合金，被称为高比重合金、重合金、和高密度钨合金。典型的钨合金组织结构是钨颗粒均匀地镶嵌在塑性良好的面心立方Ni－Fe－W固溶体基体中，并且由于烧结过程中界面能对于溶解和析出的调节作用，通常钨合金组织结构中钨颗粒近似呈球形且大小基本均匀。钨颗粒相（b.c.c结构的钨）强度较高，黏结相（f.c.c结构的Ni－Fe－W合金）强度相对较低、韧塑性却极好，这种具有强烈性能反差的组成相就注定了该材料的失效特征有别于其他常规材料。钨合金的两相复合结构决定了其宏观的变形和破坏机理与材料的微观结构密切相关，因此研究钨合金受载时微观结构的变形过程从而建立微观结构和宏观力学行为之间的关系，对后继从材料制备的角度提高钨合金力学性能有现实的指导意义，对钨合金材料的优化和力学性能的改进是十分必要的［1］。

自二战以来，各国对钨合金的力学行为的研究一直给予高度的重视，经过数十年的发展，已经在加载手段、测试技术、材料的动态响应、性能、破坏以及动态变形和断裂微观机制等研究领域做了大量的科研工作［2－9］。为了能够更好地研究颗粒增强金属基复合材料的力学行为，有效地指导该材料的加工变形工艺制定及模具设计，用计算机来模拟和预测复合材料力学性能是目前国际上的一个热点问题。在细观力学的基础上，构造出能够反映复合材料微观结构的有限元模型，考察单胞模型在载荷作用下的力学响应，进而研究复合材料的宏观力学性能。Bohm［10］等采用多夹杂单胞方法研究了随机取向短纤维增强金属基复合材料弹性和弹塑性行为。Eckschlager［11，12］等利用立方体单胞夹杂增强颗粒模型研究了增强颗粒的破碎失效行为及颗粒分布对颗粒增强金属基复合材料（PMMCs）的力学行为和起始破坏的影响。Song［13］采用均匀化理论结合不动点迭代法研究了钨合金颗粒形状、大小，体积分数对钨合金材料力学性能的影响。Leon和Mishnaevsky［14］针对不同微观结构的碳化硅增强铝基复合材料的变形和损伤演化进行了三维有限元模拟。Bao［15］等利用三维模型研究了PMMCs在高应变率下的变形行为，指出由于增强颗粒的影响，复合材料的应变率硬化要远远高于基体，并且与颗粒的百分含量有关。

1 钨合金三维有限元单胞模型

假定颗粒增强复合材料的复合相是周期分布的，材料可以看做是一个具有周期变化的无限大线弹性固体。因而，这种周期结构可看作为单位体元在各个方向周期重复扩展构成。单胞有限元模型假设单胞中只有一个位于单胞对称中心位置的增强颗粒［16］，根据周期性排列条件，单胞形状为六棱柱形或者是六面体形，如图1，2所示。增强颗粒的几何形状可以是球体、圆柱体、椭球体，颗粒的体积分数可以用颗粒占单胞的体积百分比表示。

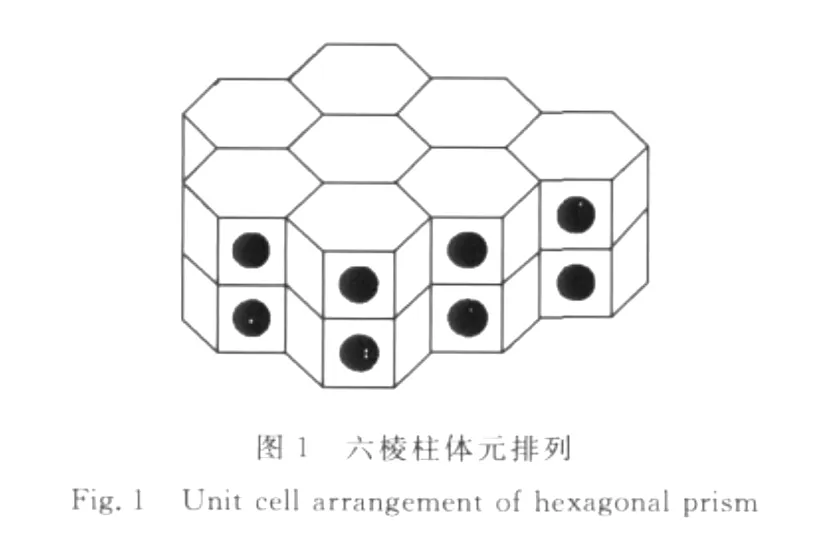
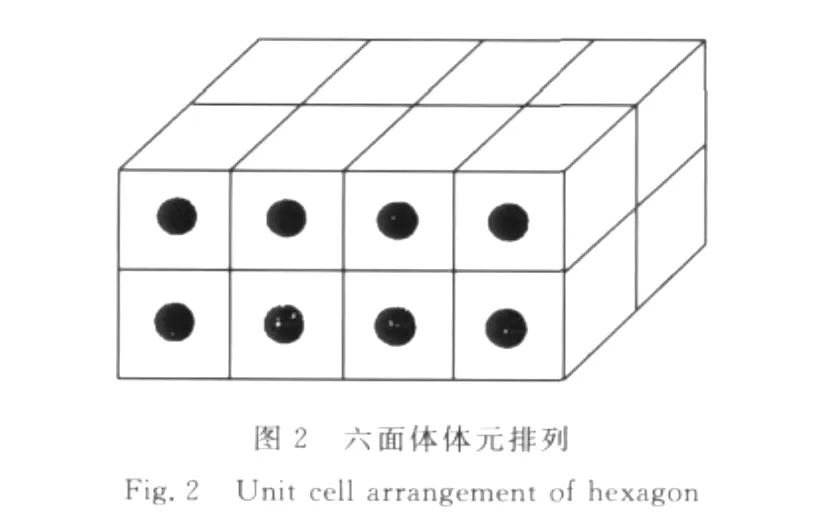
图1中对半径为r的颗粒，六棱柱体元排列的颗粒体积分数为

其中R是六棱柱体元的边长，2R为高度。

六面体体元排列的颗粒体积分数为

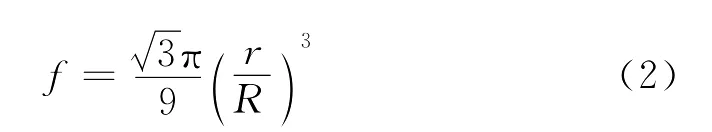
其中2R＝l是六面体体元的边长。

1.1 三维单胞模型

代表性体积单元钨颗粒相的体积分数应该与实际合金材料的钨颗粒相的体积分数保持一致

其中Vf为钨颗粒相的体积分数，vf为单胞模型中钨颗粒相的体积，v为单胞模型的总体积。基于真实的钨颗粒分布情况，在计算中采取下列假设：

（1）钨合金为宏观均质材料；

（2）钨颗粒形状为球形或者椭球状，且大小均匀；

（3）模型中假设钨颗粒和基体的界面结合完好，无滑移和分层现象。

根据以上假定和体积分数的要求，在单胞模型的建立过程中钨颗粒分布采用图3所示的排列方式。三维有限元模型如图4，5所示。由于模拟计算很关注单胞中应力、应变的分布，为了捕捉界面附近应力、应变的变化，要求较高的网格密度。

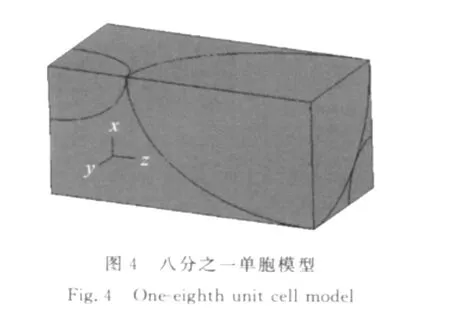
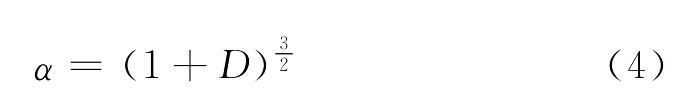
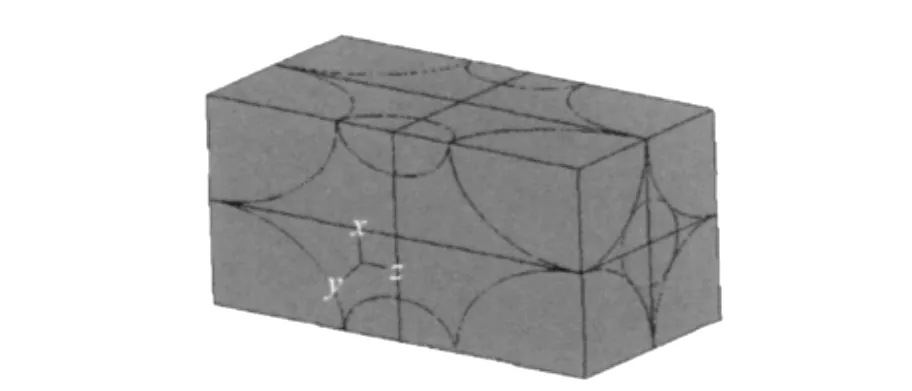
图5 单胞模型Fig.5 Unit cell model

其中，D是钨合金材料的工艺处理变形量。

经过计算，在该模型中，钨颗粒所占的体积分数约为80%。考虑到在实际的钨合金材料的基体相中，钨颗粒也同样占有一定的体积分数，同时计算中也会有一定的误差，综合考虑建立的模型可以满足实际的要求。

在进行有限元模拟分析时，一般假设钨颗粒和基体的界面是理想的，在变形过程中钨颗粒是完好无损的，在进行有限元计算时，通过对单胞体元的表面施加一定的速率或者位移，来考察复合材料的力学性能。在三维有限元数值计算中，体元的边界条件必须使体元的变形满足连续性条件和周期性条件，对立方体和长方体而言，由于其对应各面是平行的，故边界条件比较简单，只要限制各面在变形过程中平行地移动就能满足连续性条件。

1.2 材料模型与材料参数

在分析计算时，假定基体与钨颗粒之间的界面结合完好，不考虑热残余应力的影响。增强钨颗粒为线弹性材料，基体为弹塑性材料，应用Cowper－Symonds本构模型来描述材料的应变率效应：

式中：E为材料的弹性模量；σs为名义屈服应力；Ep为塑性硬化模量；εp为有效塑性应变；β为应变率因子；˙ε为应变率；C，P为描述材料应变率效应的参数；Et为切线模量。增强相和基体相材料力学性能参数见表1。

表1 钨颗粒与基体相材料的力学性能参数Table 1 Mechanical parameters of tungsten particle and matrix

2 动态拉伸实验

冲击拉伸加卸载实验是在旋转盘式间接杆－杆型冲击拉伸实验装置上进行的。图6为实验装置示意图，SHTB实验装置由旋转盘式加载系统、撞块、输入杆和输出杆组成。加载装置是一个直径为1.4m，转动线速率可以达到100m/s的飞轮。

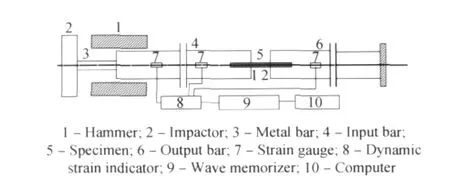
图6 实验装置Fig.6 Experimental setup

试件为哑铃形扁平状，试件尺寸如图7所示。为减小试件拉伸段圆弧部分的应力集中现象，在粘接前要把实验段的圆弧部分沿纵向研磨光滑。本实验是在室温（14℃）条件下进行的，针对91%细化钨合金材料，分别采用两种应变率200s－1和500s－1进行动态拉伸实验研究，获得了钨合金材料在不同应变率条件下的应力应变曲线和动态力学参数。

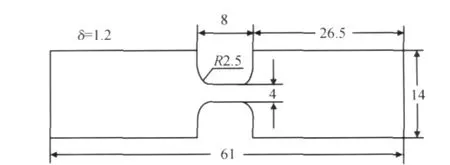
图7 试件形状和尺寸Fig.7 Schematic of experimental specimen

3 计算结果及分析

应用上述材料模型和单胞模型，分别在应变率为200s－1和500s－1下，对长细比为1的钨合金材料在单向拉伸载荷作用下的力学响应进行数值模拟。计算所得的应力应变曲线与实验所测应力应变曲线的对比如图8所示。

从图8可以看出，在动态加载条件下二者具有较好的一致性，尤其在弹性阶段吻合较好。当进入塑性阶段后，数值计算所得的弹性模量和强化模量略高于实验结果，原因可能为数值模拟是假定颗粒与基体的界面结合完好，没有考虑界面的结合力对模型承载能力的影响，而在实际情况中，实验材料不可避免地存在一些界面的破损、初始裂纹和孔洞，进而降低了材料本身的力学性能。另一方面，从图8还可以观察到，钨合金材料具有一定的应变率敏感性，随着应变率的增加其屈服强度也有一定程度的提高。

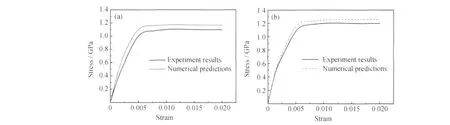
图8 不同应变率下计算结果与实验结果的对比 （a）应变率200s－1；（b）应变500s－1Fig.8 Comparison of numerical predictions with experimental results at different strain rates（a）strain rate：200s－1；（b）strain rate：500s－1

图9分别给出在应变率为200，500s－1动态加载条件下单胞模型的应力应变云图。

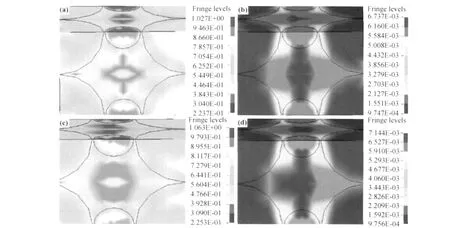
图9 不同应变率条件下单胞的应力和应变云图 （a），（b）应力、应变云图：应变率200s－1；（c），（d）应力、应变云图：应变率500s－1Fig.9 Stress distribution and strain distribution of a unit cell at different stain rates （a），（b）stress distribution and strain distribution at strain rate of 200s－1；（c），（d）stress distribution and strain distribution at strain rate of 500s－1

从以上应力应变云图可以看出，应力主要集中在钨颗粒上，对于应变而言，基体相则大于钨颗粒，且在钨颗粒和基体的交界处应变值较大，因而在拉伸载荷的作用下，钨颗粒相和基体相之间的狭长区域将首先发生破坏。

4 结论

（1）建立了具有典型微观结构钨合金三维有限元单胞模型，并对钨合金在动态拉伸载荷作用下的力学响应进行了分析。

（2）得到了钨合金的应力－应变曲线，发现钨合金具有一定的应变率敏感性，随着应变率的增加其屈服强度也在增加。

（3）通过对单胞应力应变云图的分析可以得出这样的结论：应力会在钨颗粒与基体之间的界面上集中，容易导致裂纹的产生。

［1］ 范景莲.钨合金及其制备新技术［M］.北京：冶金工业出版社，2006.

［2］ RAMESH K T，COATES R S.Microstructure influence on the dynamic response of tungsten heavy alloys［J］.Metallurgical Transactions A，1992，23A（9）：2625－2630.

［3］ 刘宝华.锻造态93wt.%钨合金动态拉伸力学性能研究［D］.北京：北京理工大学，1996.

［4］ 曾元金，经福谦，张万甲.钨合金的层断裂强度研究［J］.高压物理学报，1992，6（1），58－69.

［5］ 刘海燕，宋卫东，宁建国.不同晶粒度钨合金动态力学性能研究［J］.材料工程，2007，（6）：3－7.

［6］ WOOWARD R L，BALDWIN N J，BRUCH I et al.Effect of strain rate on the flow stress of three liquid phase sintered tungsten alloys［J］.Met Trans，1985，16A（11）：2031－2037.

［7］ LIU Hai－yan，SONG Wei－dong，REN Hui－lan.Dynamic response of tungsten－nickel－iron composites under impact loadings［J］.International Journal of Nonlinear Sciences and Numerical Simulation，2009，10（8）：993－1004.

［8］ SONG Wei－dong，NING Jian－guo，LIU Hai－yan.Study on the fracture behavior of W－Ni－Fe heavy alloys［J］.International Journal of Modern Physics B，2008，22（31－32）：5453－5458.

［9］ 黄石松，宋卫东.钨合金材料的动态拉伸实验研究［J］.材料工程，2008，（6）：9－12.

［6］ TANIO NORIHISA，KATO HISAO，KOIKE YASUHIRO，et

［10］ BOHM H J，ECKSCHLAGER A，HAN W.Multi－inclusion unit cell models for metal matrix composites with randomly oriented discontinuous reinforcements［J］.Computational materials science，2002，25（1－2）：42－53.

［11］ ECKSCHLAGER A，HAN W，BOHM H J.A unit cell model for brittle fracture of particles embedded in a ductile matrix［J］.Computational materials science，2002，25（1－2）：85－91.

［12］ HAN W，ECKSCHLAGER A，BOHM H J.The effects of three－dimensional multi－particle arrangements on the mechanical behavior and damage initiation of particle－reinforced MMCs［J］.Composites science and technology，2002，61（11）：1581－1590.

［13］ SONG W D，LIU H Y，NING J G.Tensile property and crack propagation behavior of tungsten Alloys［J］.International Journal of Modern Physics B，2011，25（11）：1475－1492.

［14］ LEON L，MISHNAEVSK Y Jr.Three－dimensional numerical testing of microstructure of particle reinforced composites［J］.Acta materialia，2004，52（14）：4177－4188.

［15］ BAO G，LIN Z.High strain rate deformation in particle reinforced metal matrix composites［J］.Acta Mater，1996，44（3）：1011－1019.

［16］ 方岱宁，齐航.颗粒增强复合材料有效性能的三维数值分析［J］材料导报，1996，28（4），475－477.

Three Dimensional Numerical Analysis on Dynamic Mechanical Property of Tungsten Alloys

LIU Hai－yan1，SONG Wei－dong2，LI Jian－qiao2
（1School of Aerospace Engineering，Beijing Institute of Technology，Beijing 100081，China；2State Key Laboratory of Explosion Science and Technology，Beijing Institute of Technology，Beijing 100081，China）

Dynamic behavior of tungsten alloys under impact loadings was investigated by using numerical simulations.Three dimensional finite element unit cell models with typical micro－structure of tungsten alloys were established.The dynamic mechanical properties of tungsten alloys under tensile loadings were investigated by numerical simulations.The effect of strain rates on the mechanical properties was analyzed.The stress and strain contours of the unit cell model at different strain rates were given.The reliability of the finite element models was verified through the comparison with experimental results.

tungsten alloy；dynamic mechanical property；micro－structure；numerical simulation

O347.1

A

1001－4381（2012）06－0071－05

国家自然科学基金（91016013；10772024）；国家重点基础研究发展计划（2010CB8327006）；新世纪优秀人才计划资助项目

2011－02－25；

2011－09－15

刘海燕（1963－），女，副教授，主要从事材料动态力学性能的研究，联系地址：北京理工大学理学院（100081），E－mail：liuhy58＠yahoo.com.cn

宋卫东，联系地址：北京理工大学爆炸科学与技术国家重点实验室（100081），E－mail：swdgh＠bit.edu.cn