低复杂度的快速降尺寸视频转码算法
吕卓逸,贾克斌,萧允治
(1. 北京工业大学 电子信息与控制工程系,北京 100124;
2. 香港理工大学 电子资讯与工程系,香港 九龙 999077)
1 引言
H.264是一种面向未来 IP和无线网络传输环境下的视频压缩标准,在压缩高效性和传输可靠性方面优于其他标准[1]。随着网络技术的飞速发展,H.264在各个领域中得到了广泛应用,基于H.264的视频编码及转码技术成为近年来国内外研究的热点。
由于网络种类的多样性(如Internet网、电信网和蜂窝无线网等),终端设备性能(如显示分辨率、处理能力和存储能力等)的差异,使得提高视频码流在不同应用环境之间的兼容性变得十分重要[1]。转换空间分辨率的视频转码,为支持各类视频显示设备提供了有效的解决方法,它将原始分辨率的视频码流转换为适合接收端显示的目标分辨率码流。
理想的视频转码器应具备低运算复杂度,高转码质量等性能。运动估计和多尺寸帧间模式预测是H.264编码中非常关键且耗时的模块,为视频转码带来极大的运算负担,影响到算法的实时性[3]。因此,如何有效利用输入码流中的编码信息来提高转码速度成为视频转码研究中的关键问题。对此,众多科研人员做了大量工作来优化转码器。文献[2]联合宏块的空间和时间特性,通过计算率失真代价从前一参考帧中选择最优编码模式。针对基于像素域的转码运算复杂度高的问题,许多基于压缩域的转码框架相继出现。文献[3]提出的合并分裂算法,在DCT(discrete cosine transform)域内实现了降尺寸转码。但是此类方法在重量化过程中易引入误差产生漂移(drift),影响转码图像质量。因此,如何提高转码效率的同时保证图像质量仍然是一个有待探索的课题。
支持向量机(SVM, support vector machine)是由Vapnik提出的一种学习机制,近几年来成为模式识别与机器学习领域研究的热点[4]。SVM以统计学习理论为基础,基于结构风险最小化原则,有效地避免了经典学习方法中过学习、维数灾难、局部极小等传统分类存在的问题。在解决小样本、非线性和高维模式识别问题中表现出明显优势[5]。现已广泛应用于文本识别、人脸识别、三维图像识别和生物信息学等方面。本文首次将SVM理论应用于基于H.264的降尺寸视频转码中,针对特征向量及核函数的选取,分类器决策树结构的设计展开研究。
本文提出一种将SVM的理论应用于快速降尺寸视频转码的方法。首先从输入的高分辨率视频码流中提取模式特征组成多维特征向量训练SVM分类器模型,建立高分辨率视频编码信息与降尺寸视频宏块编码模式之间的相关性。然后设计构建出分层式SVM分类器,对降尺寸视频中宏块的预测模式进行分类,以此缩减预测模式数量,实现转码的再编码过程中率失真优化算法的提前终止,达到降低转码运算复杂度的目的。
本文在第 2节中介绍 H.264帧间模式选择算法,第3节详细论述基于SVM的降尺寸转码快速模式决策算法,第4节给出实验结果及分析,最后是结束语。
2 H.264帧间模式选择
H.264编码标准支持7种不同块大小的帧间编码模式。每个宏块可按照 16×16,16×8,8×16,P8×8进行第1层的大块模式分割,如果选择P 8×8模式,还可按照 8×8,8×4,4×8,4×4 进行第2 层的小块模式亚分割[6]。
另外,帧间编码还采用直接拷贝模式(SKIP),帧内预测模式I4MB和I16MB。因此,H.264帧间模式选择算法流程如下。
1) 对宏块的大块模式 16×16,16×8,8×16 进行运动估计,利用式(1)计算率失真代价(RDO, rate distortion optimal)。其中D是宏块的失真,R是需要编码的信息码率,λ是用来调节失真与码率权重的Lagrange系数。
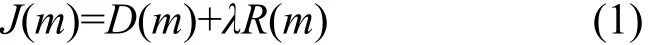
2) 对每个 P8×8块的小块模式 8×8,8×4,4×8,4×4进行运动估计,并计算其RDO,选择RDO最小的模式作为P8×8块的最佳模式。
3) 计算SKIP模式的运动矢量和RDO值。
4) 计算帧内编码模式I4MB和I16MB的RDO值。
5) 从 16×16,16×8,8×16,P8×8,SKIP,I4MB和I16MB中选择RDO值最小的模式作为帧间宏块编码模式。
由于需要对每一种候选模式进行运动估计和率失真代价的计算,使得编码计算量急剧增加,编码速度下降。为此,本文利用基于SVM的快速模式选择算法实现了低复杂度的降尺寸视频转码框架。算法的提出以输入码流中编码信息与降尺寸视频中宏块编码模式间有着较强相关性为依据,将H.264模式选择问题转化为模式分类问题,即依据编码信息将预测模式按其特征划分为不同的类别,以此减少计算率失真代价的模式数量。
3 基于SVM的转码模式快速选择算法
如上所述,H.264编码器的运算复杂性为引入机器学习方法来提高视频转码速度带来了良好契机。支持向量机方法是建立在统计学习理论中 VC维(vapnik chervonenkis dimension)[7]理论和结构风险最小原理基础上的。对训练样本集(x1,y1),…,(xl,yl)∈RN×{±1},其中,xl是从输入的高分辨率视频码流中提取的特征向量,yl为低分辨率视频中相应宏块的编码模式,N为样本特征(特征向量)空间的维数。SVM的目标是求解能够将2类样本正确分开,且使得分类间隔最大的最优分类线。对于非线性可分情况,SVM通过映射 Φ 将非线性问题转换为高维特征空间中线性问题,利用核函数 K(xi, xj)代替最优分类面中的内积,求解最优分类面的目标函数:
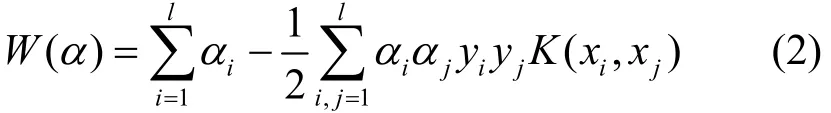
鉴于SVM在模式识别等领域,尤其在解决较复杂分类问题方面表现出来的优越性,本文提出了基于SVM的转码模式快速选择算法。
3.1 分层式SVM分类器
一般来说,视频序列中分布均匀的区域,例如背景区域,通常采用大块分割模式(16×16,16×8,8×16),而分布不均匀的区域和边缘部分通常采用小块分割模式(8×8,8×4,4×8,4×4)。同时,视频序列中相邻图像之间普遍存在着时间相关性,即相邻图像的大部分区域的变化是比较缓慢的,如背景区域中SKIP模式占有相当大的比重,而处于较长时间静止不动或者变化缓慢区域内的宏块通常采用大块分割模式。因此,利用从输入码流中提取的编码信息,减少预测模式,仅对少量可能性大的模式计算率失真代价,将有效降低转码的运算复杂度。
SVM方法最初用于数据二分类问题[8],多分类问题是被分解为多个二分类问题来实现的。目前的多分类算法,例如一对多(one against all)和一对一(one against one)等存在的共同问题是:多数量的二分类问题需要进行大规模的标准二次型优化,造成训练过程速度慢、算法复杂难以实现以及预测运算量大等问题。为了避免多分类器的弊端,本文采用基于二分类的SVM分类器以期获得更加准确的预测结果和更优的转码效果。
本文构建的分层式 SVM 分类器由以下 3个SVM二分类器组成,在降尺寸视频转码编码器中对宏块进行阶梯式模式决策。
1) 顶层分类器划分SKIP模式和non-SKIP模式。如果当前宏块被划分为 SKIP模式,则仅预测帧间16×16模式和SKIP模式。换而言之,此分类器用于划分出位于纹理分布较均匀或运动平缓区域的宏块。
2) 中间层分类器划分帧内模式和帧间模式。被划分为帧内模式类别的宏块,表明其具有运动剧烈或纹理复杂的特征,采用Intra-refresh模式编码。
3) 下层分类器对在顶层和中间层SVM分类器中被划分为non-SKIP模式和non-intra模式的宏块进行细分,划分为大块分割模式和小块分割模式。
为了保证转码后视频具有较高质量,本文对通过SVM分类后的编码模式进行小范围的模式修正,以牺牲少量运算量为代价来获得更加准确的决策模式。模式修正策略的具体思想是:如果当前宏块被划分为大块分割模式,则预测{inter16×16, inter16×8, inter8×8}和SKIP模式;如果当前宏块被划分为小块分割模式,则预测 7种帧间模式,SKIP模式和帧内模式。算法流程如图1所示。
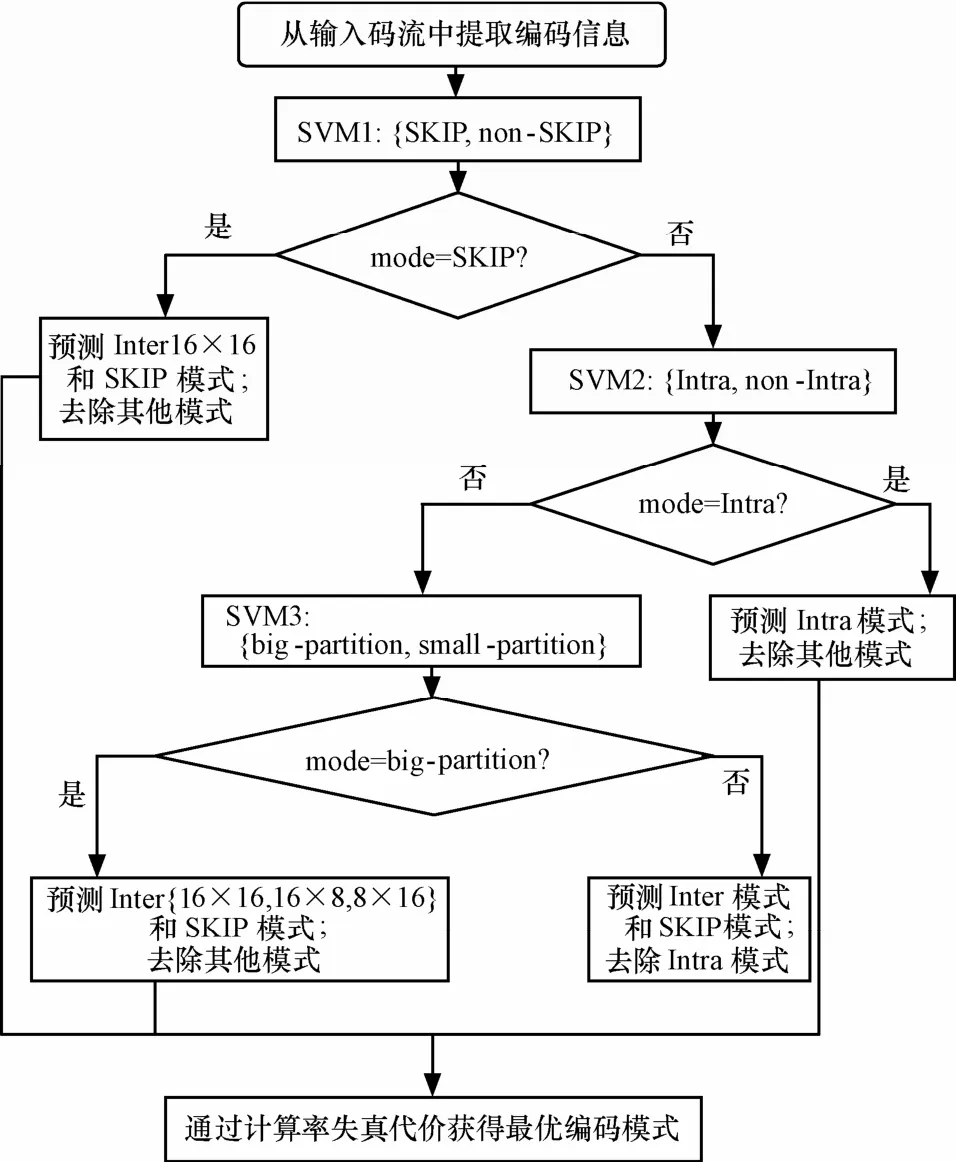
图1 算法流程
分层式SVM分类器实现了模式选择的阶梯式预判,通过缩减预测模式数量提前终止率失真优化算法,达到降低算法复杂度的目的。图2描述了基于SVM的视频转码器实现框。首先,从高分辨率视频码流中提取编码信息作为特征向量组成 SVM训练样本集。其次,利用SVM模型建立的分层式分类器得到最终预测模式,实现低复杂度的H.264视频转码。本文采用离线方法进行SVM模型的训练及预测,因此不会对转码器带来额外的运算负担。

图2 基于SVM的转码模式选择
3.2 特征向量的选取
作为 SVM 理论中的关键技术,特征向量的选取直接影响着 SVM 分类器的准确度,是构建SVM分类器的关键。特征向量的选择应满足与宏块编码模式具有强相关性的原则,而直接利用输入的视频码流中的编码信息作为特征向量组成样本集得到的分类准确度较低,因此需要对原始数据进行预处理。针对本文提出的3层式模式分类体系,选取4个特征向量分别组成各层分类器的训练和预测样本集。
首先,本文针对降尺度因子为1/4的视频转码进行研究,最直接的方法是选择在高分辨率视频的4个相邻宏块中编码模式出现频率最高的作为当前宏块的编码模式。实验数据表明,通常情况下,出现频率最高的模式往往是通过率失真优化算法得到的最终编码模式,尤其是当编码模式为SKIP模式和大块分割模式时。表1中数据是由式(3)计算获得,其中,Pmodei表示高分辨率视频的4个相邻宏块中使用频率不小于2的编码模式数量(Hmodei)与降尺寸视频实际采用该模式数量(Lmodei)的比例。因此,宏块编码模式在高分辨率视频中的出现频率被选作特征向量之一。
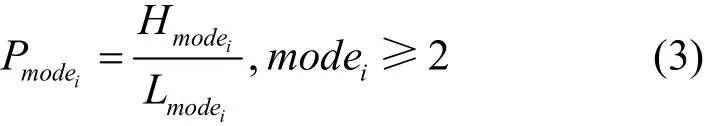

表1 出现频率与编码模式相关性
其次,帧间模式中各尺寸块的选择对编码质量有着重要影响。选择大尺寸块意味着编码运动矢量和帧间分割模式占用比特较少,而运动剧烈区域内宏块在运动补偿后的残差较大;相反,如果选择小尺寸块则残差较小,而大量的比特耗费在编码运动矢量和帧间分割模式上。本文将运动矢量和宏块残差作为下层SVM分类器的特征向量,并通过数据预处理来提高预测准确度。利用统计计算方法将运动矢量转换为运动矢量绝对值之和,将宏块残差转换为残差均值。经过预处理之后的样本集,类别分布更加清晰,模式表述更加明确。
另外,鉴于残差块不为零的 DCT系数与宏块特征的紧密联系,且其提取方法简单,无需进行DCT逆变换,因此选为上层分类器的特征向量。最后,将降尺寸视频中宏块编码模式规范为 6类:SKIP、non-SKIP、intra、non-intra、big-partition 和small-partition。
综上所述,分层式SVM分类器的特征向量FV1,FV2和FV3分别包含如下属性。在对预测准确度的分析比较中(表 2)可以看到,本文选取的特征向量组成样本集达到了较理想的训练和预测效果。
FV1=[原视频模式使用频率,不为零DCT系统个数]
FV2=[原视频模式使用频率,运动矢量绝对值之和]
FV3=[原视频模式使用频率,运动矢量绝对值之和,残差均值]
3.3 核函数的选择
核函数是支持向量机的重要组成部分,采用不同的核函数会组成不同的支持向量机算法。核函数、映射函数和特征空间一一对应,核函数参数的改变实际上隐含地改变了映射函数,进而改变样本数据子空间分布的复杂程度。因此,核函数的选取变得十分重要。
目前,在SVM中研究最多的核函数主要有4类:线性(linear)核函数,多项式(polynomial)核函数,径向基函数(RBF)和sigmoid核函数。总体来说,核函数可以划分为局部核函数和全局核函数2种[9]。局部核函数的学习能力较强,泛化能力较弱,而全局核函数的泛化能力较强,学习能力较弱。
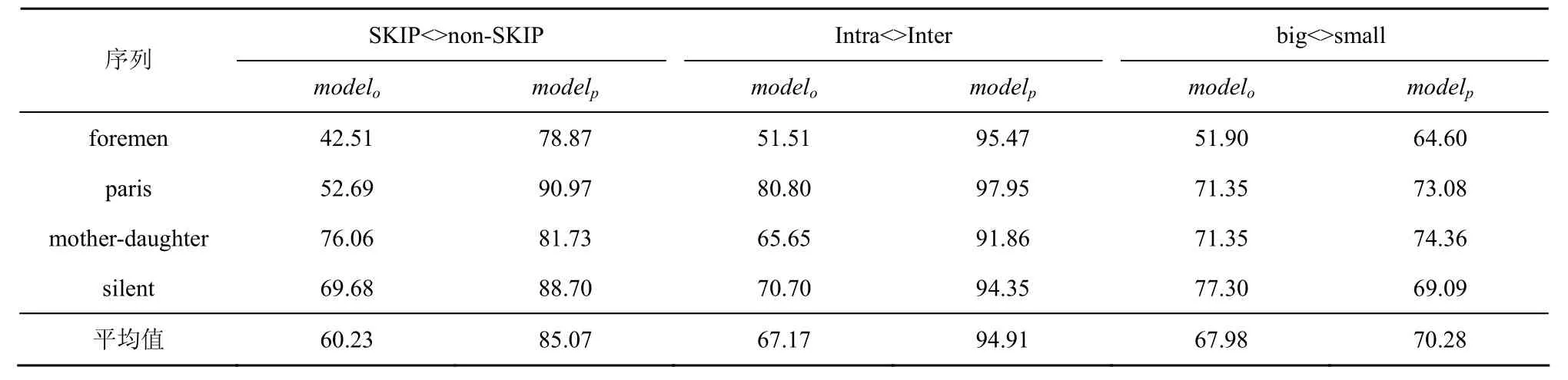
表2 运用不同特征向量获得SVM模型预测准确度/%
为了选取适用于视频转码帧内预测算法的最优核函数,本文定义了核函数性能参数 J。假设输入空间中的 2 类样本:(x1, x2,…, xl)和(xl+1, xl+2,…, x2l)分别属于类别 C1和 C2,其中 l为样本数量。各类中心点在特征空间中表示为

用核函数K(xi, xj)替代映射函数Φ,计算类中心的二次范数:
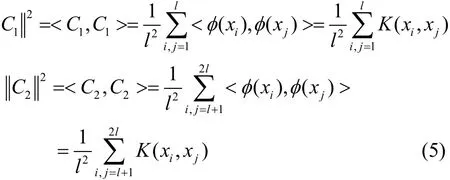
由式(6)计算获得各类紧凑度参数δ21和δ22:

类别间的中心距离为
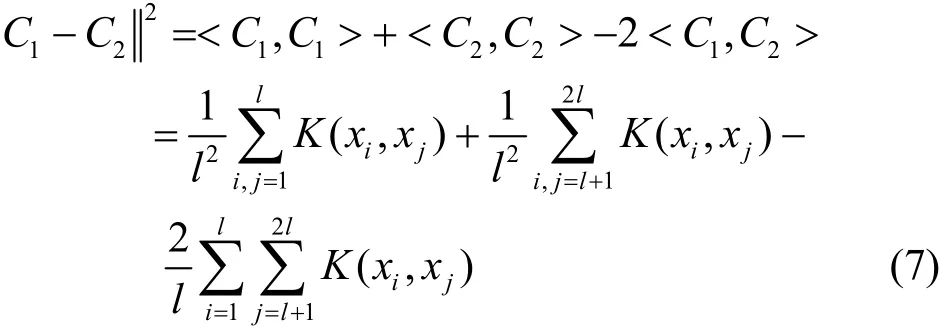
最后,得到核函数性能参数J:
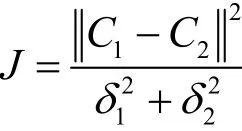
其中,分子代表不同类样本在特征空间中的可分度,分母代表同类样本的紧凑度。可见,J值越大则该核函数的性能越好。
从表3中可以看出,对于3层SVM分类器,径向基函数(RBF)的 J值最大,因此选作最优核函数进行SVM训练及预测。
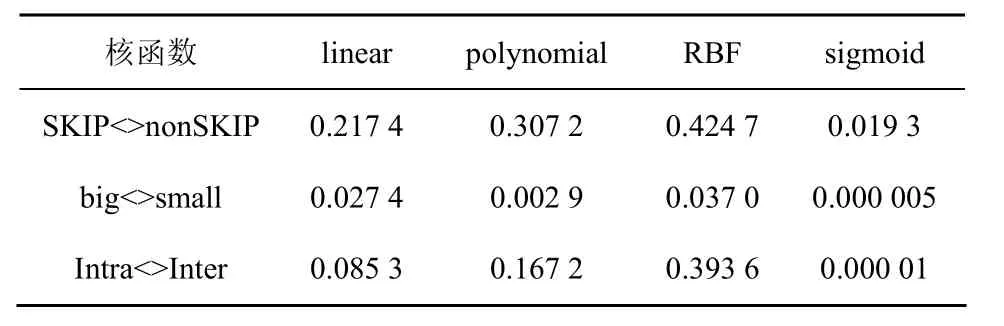
表3 核函数J值
4 实验结果与分析
在实验中,编码采用H.264的测试模型JM12.2,实验平台使用Visual C++6.0。选择开源软件libSVM[10]作为SVM开发工具,并采用离线方法训练SVM分类器,因此不会给转码器带来额外运算负担。
为了验证本文提出算法的转码效果,实验选取常用分辨率格式CIF和4CIF,共16段具有不同运动程度、纹理特征的测试序列训练SVM分类器模型。首先将高分辨率视频利用 JM12.2进行编码再解码,以便提取编码信息训练SVM模型。然后将CIF格式视频 Foreman,Mother-daughter、Paris和Silent,以及4CIF格式视频Crew、Harbor、Ice和Soccer以1/4尺寸缩小。编码采用首帧为帧内编码(intra-frame,I帧),后续帧为帧间编码(inter-frame,P帧),QP设置从22~32。
为评估本文选取特征向量的优劣,实验中另外选用文献[4]中使用的特征向量 FVo1,FVo2和 FVo3训练SVM模型Modelo,与本文的SVM模型Modelp进行比较。
FVo1=[不为零DCT系统个数,残差均值,残差方差]
FVo2=[不为零DCT系统个数,残差均值,列差方差]
FVo3=[不为零DCT系统个数,残差均值,残差方差,运动矢量均值]
表2所示为采用不同特征向量训练SVM模型预测编码模式的准确度。可以看出,基于两组不同的特征向量,本文模型Modelp达到的预测准确度更高,平均达到83.42%,最高可达97.95%。实验用于SVM训练与预测的视频序列不同,从实验结果可以看出此SVM分类器具有很好的泛化及推广能力。
本文提出的基于SVM的视频转码快速模式选择算法,与全搜索(full mode)算法和文献[2]中提出的时空域联合帧间模式预测算法(STMP)在转码质量、比特率、预测准确度和转码速度几方面进行比较。文献[2]针对H.264编码,利用宏块的时域和空域特征对帧间模式进行快速选择;而本文针对H.264视频转码,利用高分辨率视频码流中的编码信息对低分辨率视频进行快速帧间编码。由于STMP是最新且编码效果最好的方法之一,因此作为对比算法,与本文提出的方法在转码再编码过程中进行编码效果的比较。
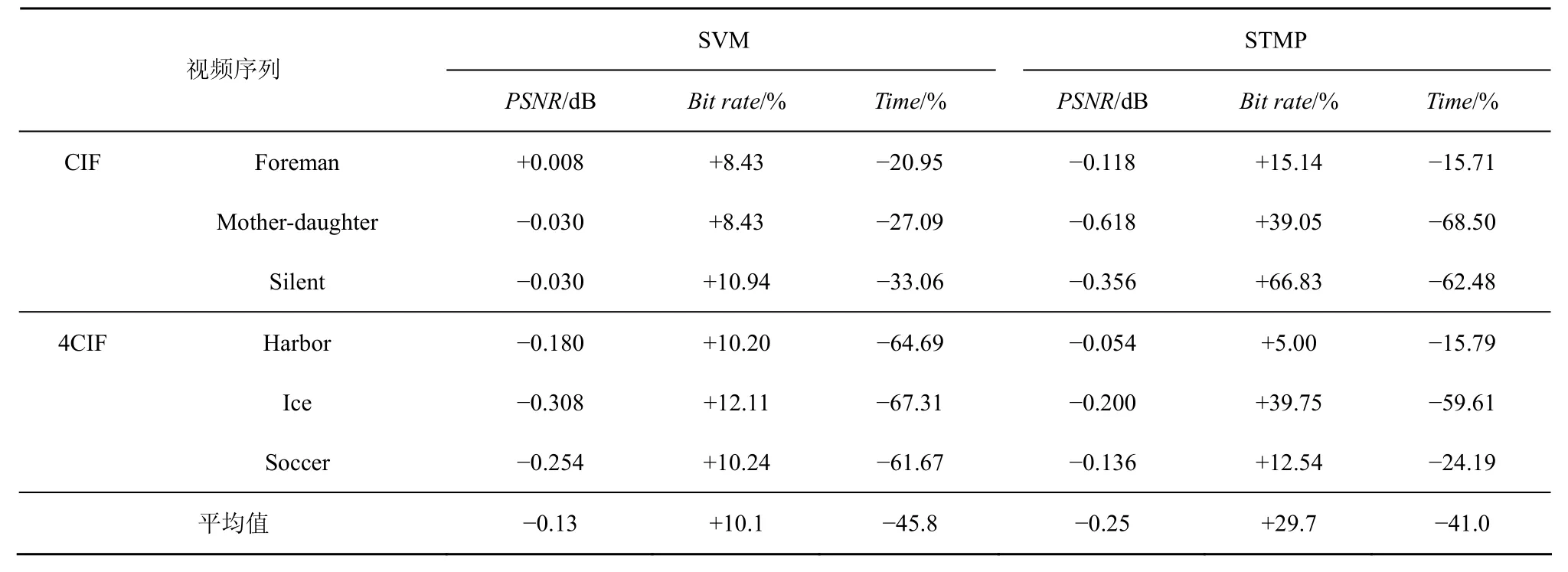
表4 几种算法进行转码效果比较
如表4(正值表示增加,负值表示减小)所示,基于SVM的模式选择算法比传统的全搜索算法平均节省45.8%时间,并保证PSNR仅下降0.13dB,比特率增加10.1%。文献[2]提出的算法STMP比full mode方法平均节省 41%运算时间,PSNR下降0.25dB,比特率增加29.7%。
另外,转码的效果与视频序列的内容,即运动快慢和分辨率有关。从PSNR和比特率2个方面考虑,利用STMP方法转码4CIF格式视频比转码CIF视频效果更好,而SVM方法转码CIF视频比转码4CIF格式视频效果更佳。对于4CIF格式视频STMP算法比SVM算法获得的图像质量稍好,但是运算复杂度较高。从图3和图4可以看出,总体来说,对于大多数视频序列而言,本文提出的基于 SVM的模式选择算法相比STMP方法达到的转码效果更好,尤其是运动剧烈的视频,例如Foreman序列等。
综合衡量运算复杂度、转码质量和压缩率等因素,本文提出的算法在有效提高降尺寸转码速度的同时,与现有算法相比,取得了更优的编码效果和更广泛的适用性。
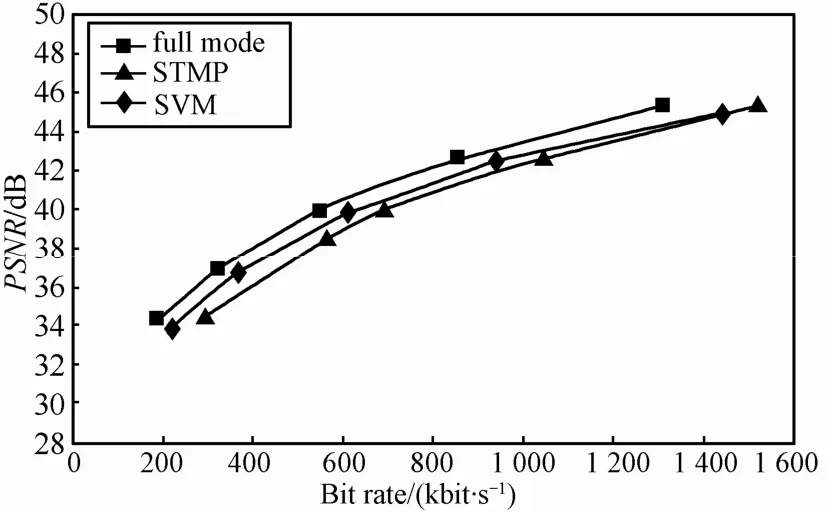
图3 Ice序列
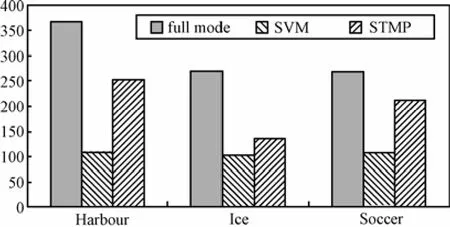
图4 算法复杂度
5 结束语
本文重点分析了H.264降尺寸转码中模式选择算法,针对视频转码运算复杂度高的问题,提出一种基于SVM的快速转码框架。利用SVM方法建立高分辨率视频码流编码信息与降尺寸视频中宏块编码模式间的联系。在此基础上,设计构建分层式SVM分类器来预测宏块编码模式。此算法缩减了预测模式的数量,实现转码再编码过程中率失真优化算法的提前终止。实验结果表明,本文提出的算法有效降低了全搜索算法的转码时间,节省了高达67.31%的运算量,并保证极小的图像质量下降。
本文专门针对基于 H.264的同类视频转码降尺寸转码中模式选择算法进行研究。由于 H.264降尺寸视频转码具有很高的实际应用价值,因此如何在提高转码后视频质量的同时有效降低编码复杂度方面仍需要进行改进。在下一步的工作中,将对运动矢量合成算法进行研究,以期进一步提高转码速度。
[1] STOCKHAMMER T, HANNUKSELA M M. H.264/AVC video for wireless transmission[J]. IEEE Wireless Communication, 2005,12(4):6-13.
[2] SONG-HAK R, YURI V, JOERN O. Fast inter-mode detection in an H.264/AVC encoder using mode and lagrangian cost correlation[J].IEEE Transactions on Circuits and Systems for Video Technology,2009, 19(2): 302-306.
[3] FUNG K T, SIU W C, DCT-based video downscaling transcoder using split and merge technique[J]. IEEE Transaction on Image Processing,2006, 15(2):394-403.
[4] JING X, SIU W C, CHAU L P, et al. Efficient inter mode decision for H.263 to H.264 video transcoding using SVMs[A]. Proceedings IEEE International Symposium on Circuits and Systems[C]. Taipei, China,2009. 2349-2352.
[5] JAEIL K, MUNCHURL K. Block-mode classification using SVMs for early terminatio of block mode decision in H.264|MPEG-4 part 10 AVC[A]. Proceedings, 2009 Seventh International Conference on Advances in Pattern Recognition[C]. Kolkata, India, 2009. 83-86.
[6] 谢晶,贾克斌. 一种基于二维直方图的 H.264/AVC快速帧内预测判决算法[J]. 电子与信息学报, 2005, 27(7):1053-1057.XIE J, JIA K B. A fast Intra-frame prediction algorithm based on two-dimensional histogram for H.264/AVC[J]. Journal of Electronics& Information Technology, 2005, 27(7): 1053-1057.
[7] VAPNIK V N. Statistical Learning Theory[M]. New York, Wiley,1998.
[8] LIU Z B, JIN L W. A new method for multi-class support vector machines[A]. Proceedings 2008 International Joint Conference on Neural Networks[C]. Hong Kong, China, 2008. 727-732.
[9] SONG H Z, DING Z C, GUO C C, et al. Research on combination kernel function of support vector machine[A]. Proceedings 2008 International Conference on Computer Science and Software Engineer[C]. Wuhan, China, 2008. 838-841.
[10] CHANG C C, LIN C J. LIBSVM: a library for support vector machines[EB/OL]. http://www.csie.ntu.edu.tw/~ lin/libsvm.

