非对称双向中继系统中的协作多址广播传输方案设计与数据率性能分析

吴丹，田亚飞，杨晨阳

(北京航空航天大学 电子信息工程学院，北京 100191)

1 引言

中继技术可以有效地扩展无线通信系统的覆盖范围或者提升用户的吞吐量[1]。在传统的半双工中继系统中，完成源节点与目的节点间的双向信息交换需要4个时隙。为了恢复半双工中继带来的频谱效率损失，最近人们提出了双向中继技术[2~5]，只需要2个时隙即可以完成双边信息交换。在双向中继系统中，根据中继处理方式不同，可以采用放大转发（AF, amplify-and-forward）[6]、解码转发（DF,decode-and-forward）[7]、估计转发（EF, estimate-and-forward）[8]或降噪转发（DnF, denoise-and-forward）[9]等多种中继转发方式。

单用户双向中继系统由基站a、用户b以及一个中继节点r组成，2个节点a、b通过中继交换信息。双向中继中2种最基本的传输方案为2时隙多址广播（MABC, multiple access broadcast）和3时隙时分广播（TDBC, time division broadcast）。在MABC方案中，第1个阶段为多址阶段，2个发射节点同时向中继发射信号，而第2个时隙为广播阶段，中继向 2个节点广播数据。研究表明，采用MABC方案的双向中继系统的和数据率是单向中继系统的2倍[10]。在TDBC方案中，在前2个时隙节点a和节点b分别向中继发射数据，中继在第3个时隙进行广播。与传统的4时隙方案比较，当中继处的2路接收信号信噪比相差不大时，TDBC可以将系统吞吐量提高1/3[11]。文献 [12] 分析并比较了这2种传输方案的容量上界和可达数据率域，结果表明MABC方案的上界始终高于TDBC方案，但在非对称信道中，MABC的可达和数据率较低。

在非对称双向中继信道中，2个源节点与中继间的信道质量不同，一端节点与中继间的信道容量较高，此时，已有的双向中继方案不能充分利用信道资源。若节点a与中继r间的信道（ar→链路）质量较好，在 MABC方案中，中继以较高的速率接收节点a的数据，而只能以较低的速率转发；而节点b正好相反，它发送的数据以较低的速率到达中继，而以较高速率被转发。当节点a已经成功接收完节点b的数据后，中继处还有大量数据需要转发至节点b。如果中继节点继续发射，则节点a转入空闲状态。在TDBC方案中，虽然可以通过控制前2个时隙的长度保证中继在第3个时隙恰好广播完双向数据，从而没有空闲时隙，但是这使得节点b在第2个时隙需要传输较长时间，导致系统和数据率依然较低。可以看出，在非对称信道双向中继系统中，较差的链路限制了双向传输的数据率，对系统性能影响很大。

在实际系统中，如蜂窝网络，由于中继位置以及信道衰落造成的信道非对称情况十分常见。另一方面，由于服务质量需求的不同，对上下行数据率的要求往往也不一样。例如，语音或视频业务对上下行数据率要求几乎相等；下载业务对下行数据率要求较高；某些网络游戏则需要较低的上行传输时延。在这些情况下，加权和数据率能更准确地反映系统性能。

目前针对非对称信道或非对称数据率的解决方案并不多。在文献[13]中，作者针对MABC方案的广播阶段，设计了采用DF中继时非对称数据率的传输方案，但没有联合考虑多址阶段的传输方案。在文献[14]中，作者针对 MABC方案设计了CF中继、非对称数据率传输的码本。在文献[15]中，作者对信号采用分层调制方式以适应非对称信道的传输特点，从而降低TDBC方案下的误比特率。这些方案缩短了可达和数据率与容量上界之间的差距，但并未提高容量上界本身。

本文提出一种非对称双向中继传输方案，称为协作多址广播方案（CoMABC, cooperative multiple access broadcast）。此方案在采用2时隙MABC方案进行传输后，引入第3个时隙，使得中继与空闲节点协作向另一节点传输。本文将研究新方案的容量上界以及DF方式下的可达数据率域，给出系统在加性白高斯噪声信道（AWGN）以及瑞利衰落信道下的性能。为了得到最大加权和数据率，将对时隙以及功率进行优化。分析结果表明，CoMABC方案能够提高非对称信道下系统的加权和容量与加权和数据率。

本文章节安排如下：第2节给出系统模型；在第3节中，提出新的传输方案，并推导新方案的容量上界以及可达速率域，对资源优化优化问题进行建模；仿真结果与分析在第4节中给出，最后是结束语。

2 系统模型

考虑最基本的单天线3节点双向中继系统，其中基站 （用节点a表示）和用户（用节点b表示）通过一个时分双工（TDD）中继（用节点r表示）相互通信。传输过程在单位时间内完成，共有M个时隙，用tm表示第m个时隙，因此

用hij表示节点i与节点 j间的信道，其中，i, j=a,b, r。在TDD系统中，假设上下行信道具有理想互异性，故hij= hji。在AWGN信道下，考虑由路径损耗所带来的信道非对称性的影响；而在瑞利衰落信道下，信道非对称性不仅与路径损耗有关，也与小尺度衰落有关。

s(m)为节点i在第m个时隙发射的比特信息，i经调制后以Rij的速率发射至节点j。调制后的数据为x(m)=M(m)（s(m)）。由于不同链路的信道条件不i,ji,ji同，为了充分利用信道资源，对发射信号采用不同的调制和编码方式，这里 Mi

(,mj

)表示第 m个时隙节点i发射至节点j的数据所采用的调制方式。调制后的信号满足能量约束E（x2）= 1。3个节点a、b、i,jr处的发射功率分别为Pa、Pb以及Pr。因此，接收机j处的接收信号可以表示为

其中，nj为零均值单位方差加性复高斯白噪声。

3 系统传输方案及性能分析

本节针对MABC和TDBC方案在非对称信道下不能充分利用信道资源的问题，设计一种新的3时隙协作多址广播传输方案，并给出采用DF中继时的可实现方案。而后，将推导所提出方案的容量上界及DF方式下的可达数据率域，并对达到加权和数据率上界及可达加权和数据率的资源优化问题进行建模。

3.1 系统传输方案

在下面的分析中，假设节点a与中继r间的信道质量优于节点b与中继间的信道。当br↔链路质量较好时，只需在下面的步骤中将节点a与节点b互换即可。

CoMABC方案考虑在MABC方案中引入第3个时隙，使得空闲节点a可以与中继节点协作发射，从而提高非对称信道下的系统性能。传输过程如图1所示。

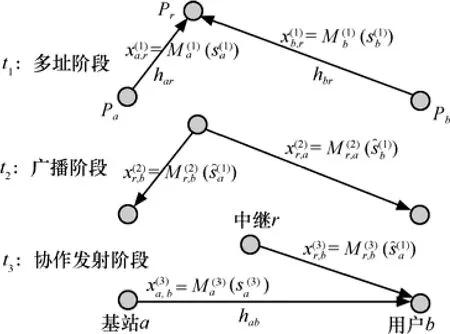
图1 协作多址广播（CoMABC）传输方案

下面提出中继 DF转发模式下的一种可实现传输方案。

第1个时隙t1为多址阶段，2节点a、b同时向中 继 发 射 调 制 后 的 数 据 x(1)=M(1)（s(1)）和a,raax(1)= M(1)（ s(1)）。中继端的接收信号为b,rbb

当中继两端信道不对称时，a、b节点发射的数据在中继处的接收信噪比相差较大。在DF模式下，中继端进行串行干扰消除，从而可以分别得到2路信号的估计值 sˆa(1)和sˆb(1)。

第2个时隙t2为广播阶段，为了适应广播信道，中继需要对2路信号重新调制后进行功率分配，并以模拟网络编码[9]的方式合并后广播。设β为功率分配因子，为r→b链路分配的发射功率为βPr，而为r→a链路分配的发射功率为(1-β)Pr。因此，t2时隙中继发射信号为

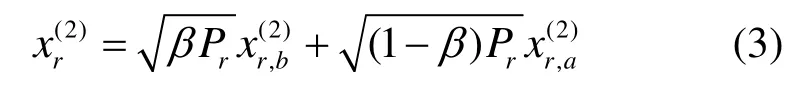
节点a和b分别接收到2路数据的和信号：

其中，j=a, b。

a、b节点均已知各自的发射数据sa和sb，因此在删除自己发射数据产生的接收信号（即自干扰信号）后，可以得到对方节点的信息。

在非对称信道下，在t2时隙结束时，中继无法完全转发节点a的数据。在第3个时隙t3，由中继和节点a同时向节点b发射数据。中继负责转发在上一个时隙未能成功转发的数据，而节点a继续发送后续数据。在t3结束时，节点b的接收信号为

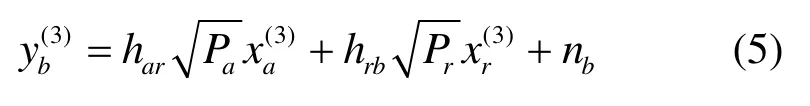
接收端对2路数据进行串行干扰消除后即可得到最终所需的数据，从而完成整个传输过程。

3.2 容量上界与可达速率域

在不考虑中继转发方式的情况下，可以推导出CoMABC方案的容量上界。对于采用DF中继的可实现传输方案，可以得到其可达数据率域。

为了与已有方案进行比较，下面首先应用半双工系统下的割集定理（cut-set theorem）[16]，推导出CoMABC方案的系统容量上界和可实现方案的可达数据率域。MABC以及TDBC方案的容量上界及可达数据率域在文献 [12] 中有详细推导。

多状态网络割集定理[17]给出了半双工中继系统的容量上界。为方便读者，并给出后面的证明中将用到的重要定义，将对其进行简要介绍。

割集定理[17]：对于有M个状态N个节点的网络，M和N均有限，割集C将节点分为2个集合S和SC（S的补集）。信息由发射节点集合S1发出，到达接收节点集合 S2， S1, S2⊂ { 1,2,… ,N }，信息速率{Rij}是可达的，如果对网络所处的任一状态均满足

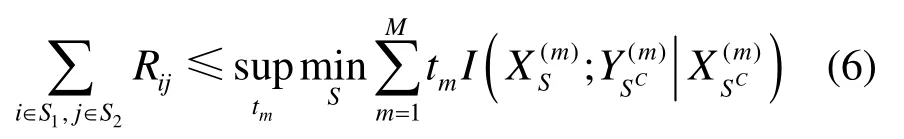
其中，S满足 S ∩ S1= S1, S ∩ S2=Ø ，非负时隙分配满足；互信息量）表示在已知集合 SC的发射信号的情况下，从集合S中的发射节点到集合 SC中的接收节点所能传输的最大数据率。

下面用割集定理推导 CoMABC方案的容量上界。

命题 1 对于半双工双向中继网络，3时隙CoMABC方案的容量上界为Ra和Rb构成的凸集，Ra和Rb满足条件：

证明 根据多状态网络的割集定理，如图2所示，网络共有3个传输状态，分别是t1时隙多址状态，t2时隙广播状态和t3时隙协作发射状态。

图2 网络割集

首先确定 b节点的发射数据率 Rb。发射集合S1= { b}，接收集合 S2= { a}。注意到 C2和 C1这 2个割(cut)分别对应于不同的、满足条件S ∩ S1= S1, S ∩ S2=Ø 的 集 合S。 C2对 应 于S = { b}，而 C1对应于 S = { r,b}。根据割集定理，应在所有满足条件的集合S上取最小，因此节点b的发射数据率如式（7b）所示。

可以采用同样的方式确定节点a的数据率Ra，注意到节点a也在t3时隙发射。发射集合 S1= { a}，接收集合 S2= { b}，2个割 C1和 C2分别对应集合S = { a}以及 S = { a,r}。因此节点 a的数据率由式（7a）给出。

式（7）给出了用互信息量表示的CoMABC方案的容量上界。在本文考虑的信道模型下，此方案的容量上界还可以表示为

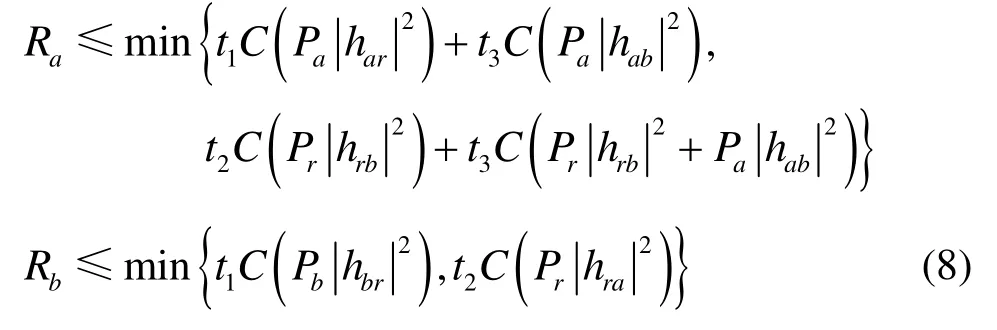
其中，C (x) = l b(1 + x )，x为接收信噪比。在AWGN信道下，信道系数h中只包含大尺度路径损耗信息；而对于瑞利衰落信道，h包含大尺度和小尺度信息。

下面的命题给出了DF方式下可实现CoMABC方案的可达数据率域。

命题 2 半双工双向 DF中继网络，3时隙CoMABC方案的可达数据率域为Ra和Rb构成的凸集，Ra和Rb满足条件：

证明 与命题一给出的上界相比，这里增加了式（9c）来约束t1时隙多址阶段的数据率。下面根据方案的具体实现过程来证明数据率域是可达的。

Rb表示节点b的发射数据率，t1时隙节点b发射数据，中继r接收并解码；t2时隙中继重新编码后以适应r→a链路的调制方式把数据转发至节点a，节点 a在删去自干扰后即可得到所需的来自节点b的信息。因此Rb由式（9b）决定。

用Ra1表示节点a通过中继转发的数据率，包括与b节点对应的前2个时隙传输的数据，以及在 t3时隙由中继单独转发的数据，因此 Ra1应该满足

其中，Rr3表示第3个时隙中继的最大传输数据率。

由于第1个时隙结束时，中继需要对a、b 2路数据分别解码，因此两端数据率受多址信道容量的限制，故有约束：

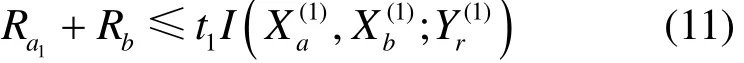
在第3个时隙，中继和节点a同时向节点b发射数据，节点b也需要将2路数据分别解出，因此t3时隙的和数据率也受多址容量的限制，有

其中，Ra3为t3时隙中节点a向节点b传输的新数据的数据率，与t1时隙的数据不同。Ra3和Rr3还应分别满足

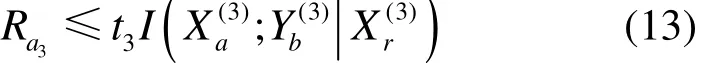
和

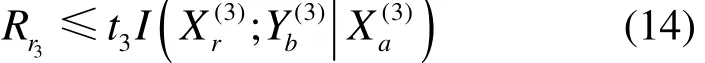
节点 a的发射数据率应为 Ra1和 Ra3之和，即Ra=Ra1+Ra3，带入式（10）、式（12）和式（13），可得到式（9a）。

最后，由于Ra+Rb=Ra1+Ra3+Rb，由式（11）和式（13）即可得到式（9c）。

可实现CoMABC方案在AWGN以及瑞利衰落信道下的可达数据率域分别可以表示为

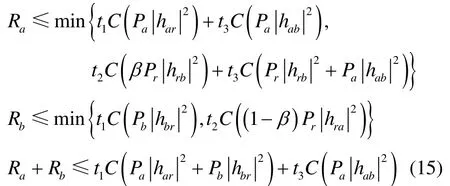
同样，在AWGN信道下，信道系数h中只包含大尺度路径损耗信息；而对于瑞利衰落信道，h包含大尺度和小尺度信息。

注意到在 DF模式下，在广播阶段需要进行功率分配，2路数据的发射功率分别为βP3和（1-β）P3，因此前2个不等式与上界中的表达有所不同。

3.3 资源分配优化问题

在得到 CoMABC方案的容量上界和可实现方案的可达数据率域后，可以对系统的加权和容量及加权和数据率进行优化。在蜂窝系统的应用场景下，如果节点a为基站，节点b为用户，则Ra为系统的下行数据率，Rb为上行数据率。系统加权和数据率为uaRa+ubRb，可以反映出上下行数据率不对称对系统性能的影响，这里，ua和ub为加权系数。当ua> ub时，Ra对加权和数据率影响较大；反之，ua< ub，Rb影响较大。当二者相等时即为和数据率。

从容量上界表达式（8）中可以看出，在节点位置信息确定后，CoMABC方案的容量上界与系统的时隙分配方案有关，因此通过对时隙分配进行优化，可以优化系统的加权和容量上界。

在单位传输时间的约束下，上述优化问题可以建模为

这是一个线性规划问题，可以通过内点法[18]得到最优解。

同样，从可达数据率域表达式（15）中可以知道，通过对功率和时隙分配进行联合优化，可以得到前述可实现方案的最大可达加权和数据率。

这个优化问题可以建模如下：

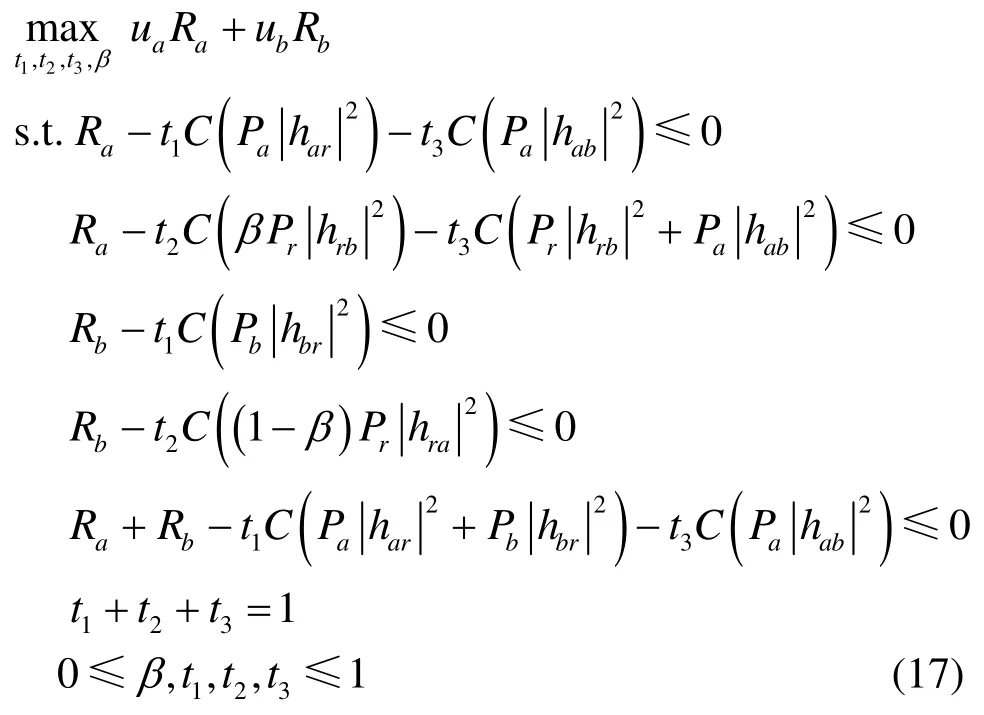
这是一个更为复杂的非线性约束优化问题。不过，可以通过有效集的方法[18]解得。

4 仿真结果与分析

本节通过仿真对CoMABC、MABC以及TDBC这3种传输方案的系统加权和容量上界进行比较，也比较在DF方式下3种方案的加权可达和数据率。

MABC方案和TDBC方案的容量上界和可达数据率域由文献[9]给出。容量上界与中继处理方式无关，因此只需优化时隙分配，即可优化这2种方案的加权和容量上界，是线性规划问题。对于DF模式下的加权可达和数据率，MABC和TDBC方案同样需要中继解码，并进行功率分配后再广播信号，因此也需要联合优化时隙与功率分配因子。上述资源优化分配的方法与CoMABC方案相似。

图3 简化系统模型

为了便于分析与仿真，设中继r位于基站a与用户b的连线上，且与a的距离为d，如图3所示，此时有当d在[0,1]之间变化时，中继位置在a和b之间移动。仿真中3节点发射功率相等，即Pa= Pb= Pr= P，接收端的白高斯噪声方差相等，均为σ2=1。在下面的仿真中，每个节点的发射功率均为Pσ2= 1 0 dB。

图4比较了在AWGN信道下，当数据率加权系数 ua= ub= 1时，CoMABC方案与MABC和TDBC方案的系统和容量上界以及解码转发方式下的可达和数据率。

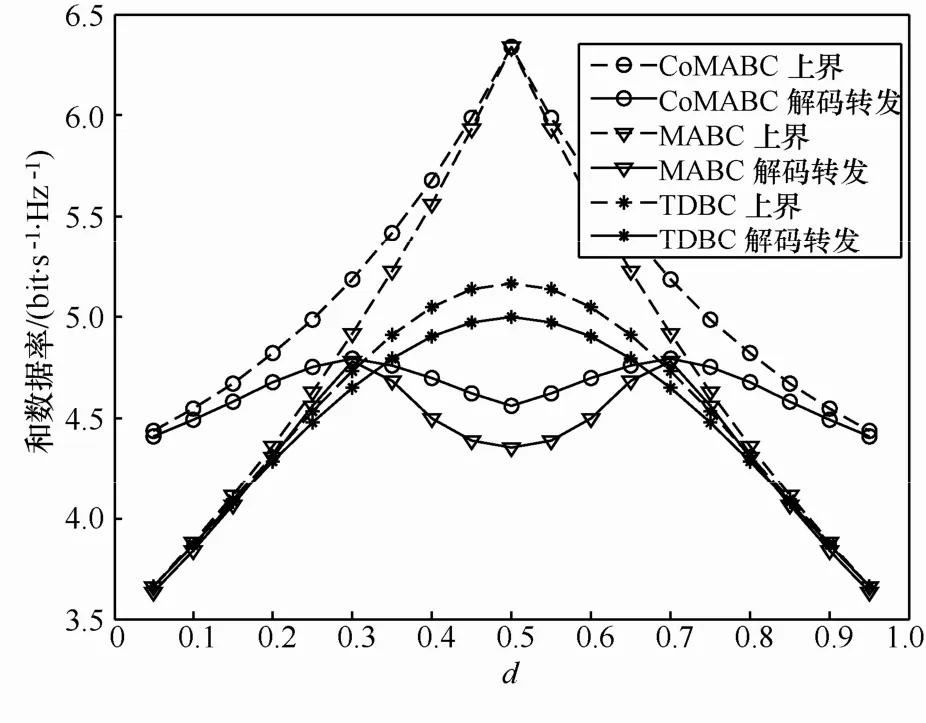
图4 AWGN信道下各方案性能

可以看出，CoMABC方案的容量上界始终高于另外2种方案，同时CoMABC方案的可达和数据率始终高于 MABC方案。当中继距离一端节点较近时，信道非对称。如d<0.3时，距离节点a较近，而d>0.7时，距离节点b较近，此时，CoMABC方案始终优于MABC和TDBC方案，表明CoMABC方案更适于非对称信道的场景。

表1给出了d=0.2和d=0.4（括号中数值）时3种方案在DF模式下的时隙与功率分配结果。

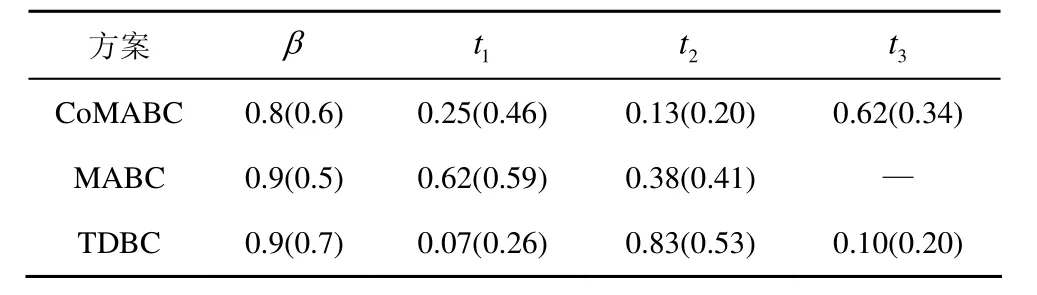
表1 d=0.2和d=0.4时，最优功率与时隙分配结果

数据表明，为了更好地分配双向数据率，功率分配的优化结果都是向广播阶段较差的一条链路分配更多的功率。在非对称信道下，我们的方案可以通过在第3个时隙进行协作发射来提高系统的和数据率。信道越不对称，第3个时隙所分配的时间越长。

图5给出了AWGN信道下d=0.2时3种传输方案的可达数据率域。

图5 AWGN信道下DF模式下可达数据率域

可以看出，3种方案所支持的双向数据率并不相同。TDBC方案的优化结果使得在广播阶段，中继能够恰好完全转发前2个时隙接收到的a、b节点的发射数据，由于ra→链路性能较好，因此Rb较高。对于CoMABC方案，由于第3个时隙中继和节点a同时向节点b传输，使得a节点发射的数据较多，Ra较大。MABC是二者的折中，两端数据率分配得更加公平。但是从和数据率上来看，CoMABC更有优势。

图6给出了不同的加权因子对系统加权和容量和加权和数据率的影响。

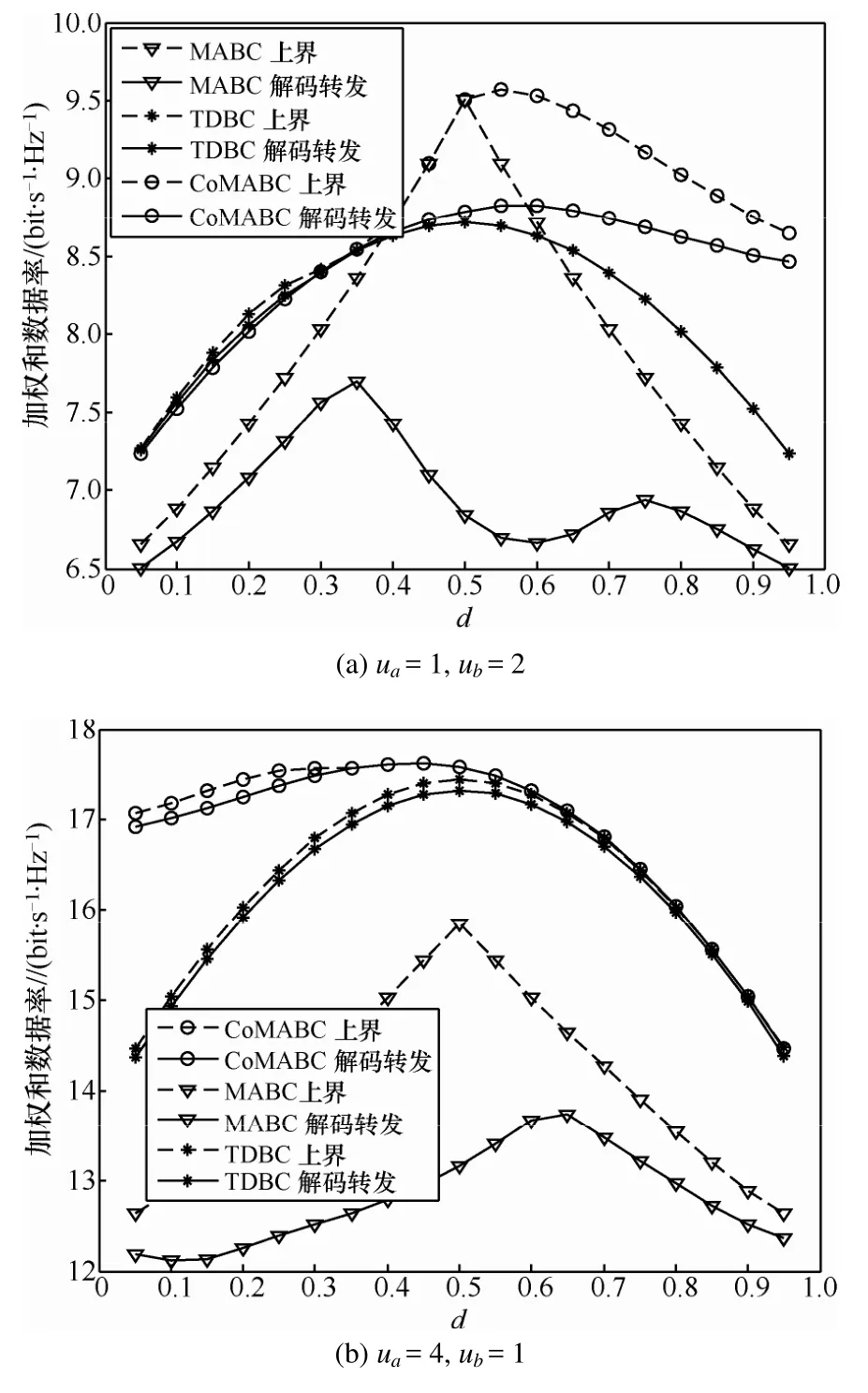
图6 AWGN信道下系统加权和容量及加权和数据率

图6 (a)给出了ua=1、ub=2时3种方案的性能。可以看出，CoMABC方案几乎始终优于另 2种方案，当中继靠近基站b时，CoMABC方案优势更加明显。因此，当用户在进行上行通信时，如果附近有中继可以协作，则可以很好地提高系统的加权和数据率。

图6(b)给出了ua=4、ub=1时，3种方案性能的比较，CoMABC方案也始终保持了最优的性能，且在节点b附近有明显优势。因此在实际系统中，基站在服务对下行数据率要求较高的用户时，应该选择距离基站较近的中继进行协作传输。

图7比较了瑞利信道下各方案的性能。

图 7(a)给出了 ua= ub=1时 CoMABC方案与MABC和TDBC方案的和容量与和数据率，该仿真结果是对1 000次信道实现进行平均的结果，对每一次信道实现都进行了功率分配和时隙优化。可以看出在非对称瑞利信道下，CoMABC方案性能依然优越，系统性能大大优于MABC和TDBC方案。

图7 瑞利衰落信道下各方案性能

如果对每次信道实现都求解一次优化问题，系统实现复杂度很高。为此，考虑根据中继位置、即根据大尺度信道信息，确定系统的功率分配因子和时隙分配，在小尺度信道衰落不同时下依然采用固定的分配方案，这样只需在各节点位置确定时进行一次优化，从而大大降低复杂度。图7(b)给出了固定时隙分配及功率分配因子时，在瑞利衰落信道下3种方案的性能。可以看出，即使时隙和功率分配并不是针对每次信道实现来优化的，在非对称信道下，CoMABC方案依然能够保持很好的性能，系统和数据率远高于MABC和TDBC方案，且与二者相比，系统和数据率随中继位置变化很小。

当加权因子不同时，上述3种方案在瑞利衰落信道下的加权和数据率与 AWGN信道下的变化趋势相同，这里不再赘述。

5 结束语

本文针对非对称信道半双工双向中继系统，提出了一种新的3时隙协作多址广播传输方案，推导了所提出方案的容量上界以及在解码转发方式下的可达数据率域，并通过优化最优时隙分配以及功率分配参数，比较了系统在白高斯信道和瑞利衰落信道下的最大加权和容量与最大加权和数据率。分析和仿真结果表明，在非对称双向中继系统中，所提出的CoMABC方案的性能优于已有方案。

[1] DOHLER M, LI Y H. Cooperative Communications: Hardware,Channel and PHY [M]. John Wiley & Sons, Ltd, 2010.

[2] LOUIE R, LI Y H, VUCETIC B. Practical physical layer network coding for two-way relay channels: performance analysis and comparison[J]. IEEE Trans Wireless Commun, 2010, 9(2):764 -777.

[3] WILSON M P, NARAYANAN K, PFISTER H D, et al. Joint physical layer coding and network coding for bidirectional relaying[J]. IEEE Trans Inf Theory, 2010, 56(11):5641-5654.

[4] ZHANG R, LIANG Y C, CHAI C C. Optimal beamforming for two-way multi-antenna relay channel with analogue network coding[J].IEEE J Sel Areas Commun, 2009, 27(5):699-712.

[5] CHEN M, YENER A. Multiuser two-way relaying: detection and interference management strategies[J]. IEEE Trans Wireless Commun,2009, 8(8):4296-4305.

[6] NGO H Q, QUEK T Q S, SHIN H. Amplify-and-forward two-way relay networks: error exponents and resource allocation[J]. IEEE Trans Commun, 2010, 58(9):2653-2666.

[7] ZHOU Q, LI Y, LAU F, et al. Decode-and-forward two-way relaying with network coding and opportunistic relay selection[J]. IEEE Trans Commun, 2010,58(9):1-7.

[8] CUI T, HO T, KLIEWER J. Memoryless relay strategies for two-way relay channels[J]. IEEE J Sel Areas Commun, 2009,57(10):3132-3143.

[9] KOIKE-AKINO T, POPOVSKI P, TAROKH V. Optimized constellations for two-way wireless relaying with physical network coding[J]. IEEE J Sel Areas Commun, 2009, 27(5):773-787.

[10] RANKOV B, WITTNEBEN A. Spectral efficient protocols for half-duplex fading relay channels[J]. IEEE J Sel Areas Commun, 2007,25(2):379-389.

[11] LARSSON P, JOHANSSON N, SUNELL K E. Coded bi-directional relaying[A]. Proc IEEE Vehicular Technology Conf[C]. 2006. 851-855.

[12] KIM S J, MITRAN P, TAROKH V. Performance bounds for bi-directional coded cooperation protocols[J]. IEEE Trans Inf Theory,2008, 54(22):5235-5241.

[13] ZHAO J, KUHN M, WITTNEBEN A, et al. Asymmetric data rate transmission in two-way relaying systems with network coding[A].Proc IEEE Int Conf Communications (ICC’10)[C]. 2010. 1-6.

[14] PAN C, ZHENG J. Mapping codebook-based physical network coding for asymmetric two-way relay channels[A]. Proc IEEE Int Conf Communications (ICC’10)[C]. 2010.1-5.

[15] PARK J M, KIM S L, CHOI J. Hierarchically modulated network coding for asymmetric two-way relay systems[J]. IEEE Trans Vehicular Technology, 2010, 59(5):2179-2184.

[16] FITZEK H, KATZ D. Cooperation in Wireless Network Principles and Application[M]. Springer, 2006.

[17] KHOJASTEPOUR M. Distributed Cooperative Communications in Wireless Networks[D]. Dept of Electrical and Computer Engineering,Rice University, 2004.

[18] 陈宝林.最优化理论与算法[M]. 北京: 清华大学出版社, 2005.CHEN B L. Optimal Theories and Methods[M]. Beijing: Tsinghua University Press, 2005.