新的混沌粒子群优化算法

胥小波，郑康锋，李丹，武斌，杨义先

(1. 北京邮电大学 信息安全中心，北京 100876；

2. 北京邮电大学 灾备技术国家工程实验室，北京 100876)

1 引言

粒子群优化(PSO, particle swarm optimization)算法是由Kennedy和Eberhart在1995年提出的一种群智能优化方法[1]。该算法因其建模简单，收敛速度快且易于实现等优点，不仅在求解组合优化问题、神经网络训练、模式分类、模糊系统控制等传统优化问题取得了显著的成效[2,3]，而且在通信、传感器网络、最优路径、资源分配、生物分子研究等领域得到了广泛的应用[4～6]。但是PSO算法在搜索的初期往往收敛较快，而在后期容易陷入局部最优。

针对此不足，Bergh等[7]提出了Multi-start PSO算法，即每迭代若干次后，都保留历史最优粒子，粒子全部初始化，以提高粒子的多样性，扩大搜索空间。Jiao等[8]提出了一种动态惯性权重的粒子群优化算法，惯性权重随着迭代次数的增加而降低，在开始阶段具有较强的全局搜索能力，而在后期以较小的惯性权重能够收敛到最优解。

混沌优化算法是一种新型搜索算法，其基本思想是把变量从混沌空间变换到解空间，然后利用混沌变量具有遍历性、随机性和规律性的特点进行搜索，混沌优化方法具有全局渐进收敛、易跳出局部极小点和收敛速度快的特点。

文献[9]提出将混沌嵌入粒子群算法的思想，在粒子与种群最优解的距离小于门限值时，进行混沌搜索，搜索到较优解则取代当前粒子。混沌粒子群算法提出后，利用混沌策略与粒子群算法的结合已有不少尝试，文献[10]提出了将分段线性混沌映射结合到粒子群 (PWLCPSO) 算法，取代了经典的logistic混沌模型。文献[11]利用混沌序列产生传统粒子群算法中的参数，提出了一种逃离局部最优解的新思路。文献[12]采用Henon混沌映射序列和隐式过滤本地搜索策略来增加收敛速度和搜索精度，可以过滤低幅振荡，快速接近较优解。文献[13]将人工免疫系统(AIS)、混沌算子、粒子群优化算法结合起来提出了一种混沌免疫粒子群(CIPSO)算法，用来解决多目标路径优化问题。

综上所述，对于混沌粒子群算法的研究目前主要集中于各种混沌映射对于算法的性能影响及利用算法混合思想与一些启发式算法相混合。现有的混沌粒子群基本思想是利用混沌序列产生新的粒子代替原来的粒子，效果并不理想。而本文并不是将混沌与粒子群算法简单地结合在一起，而是将混沌融入到粒子的运动过程中，达到了较好的效果。

2 PSO算法基本思想

PSO算法模拟鸟集群飞行觅食的行为[14]。设搜索空间为D维，总粒子数为n。第i个粒子位置表示为向量Xi=(xi1, xi2,…, xiD)；第i个粒子“飞行”历史中的过去最优位置为Pi=( pi1,pi2, …,piD)，整个种群过去最优位置 Pg为所有 Pi(i=1, …,n)中的最优；第i个粒子的位置变化率（速度）为向量Vi=(vi1,vi2,…, viD)。每个粒子的位置按如下公式进行变化：

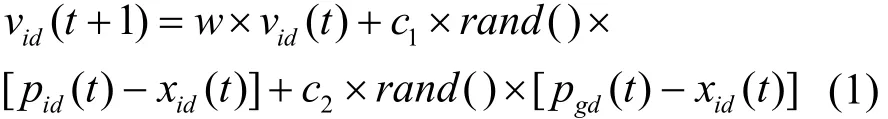
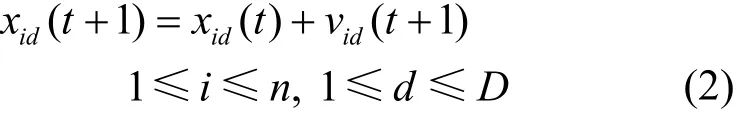
其中，c1和 c2为正常数，称作学习因子；rand()是介于[0,1]之间的随机数；w是惯性权重，可以调节算法的全局和局部寻优能力。粒子群初始位置和速度随机产生，然后按式(1)和式(2)进行迭代，直至找到满意的解。

3 混沌粒子群算法模型

3.1 算法模型

本文受文献[15]中提出的混沌蚁群（CAS）算法的启发，并在此基础上改进，结合粒子群算法，提出了如下混沌粒子群优化系统动力学模型。

其中，式(3)为粒子速度更新算法，含义与式(1)相同。式(4)为混沌变量，影响粒子的混沌程度。rid是一个小于1的正常数，定义为第i个粒子第d维的混沌因子。式(5)在粒子群的位置更新中引入混沌。t表示迭代次数，Ψd表示搜索测度，Mi表示粒子i的搜索空间向负方向移动的比例，如：Ψd=100，Mi=0.5，则表示搜索空间为[-50,50]。

混沌算法采用了文献[15]中的混沌算法，即Sole等给出的混沌系统[16]，混沌迭代如式(6)所示。

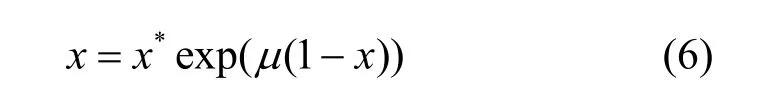
目前己有的混沌粒子群算法主要是在进入稳定状态后，用混沌序列搜索取代现有粒子。而本算法模拟粒子群混沌与稳定的交替运动过程，将混沌运动与粒子群运动结合到一起，并通过混沌因子来调节混沌程度，并提出了数学模型。

3.2 混沌变量

混沌变量在粒子群运动过程中起到控制粒子混沌程度的作用。当混沌变量Cid(t)→1时，粒子的位置更新方法为

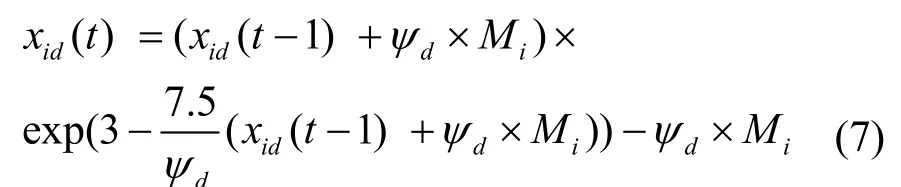
此时，式(7)为式(6)经过位置变换后的结果，主要是粒子个体的混沌在发挥作用。

而当混沌变量Cid(t)→0时，粒子的位置更新方法为

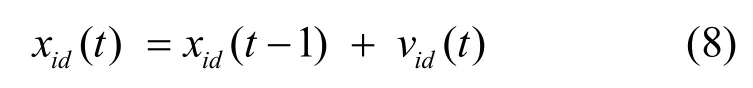
可以看出，式(8)与式(2)相同，粒子群算法起主要作用。

3.3 粒子位置更新

原粒子群算法是对所有维的位置作为一个整体更新后，再计算个体历史最优(Pid)和群体全局最优(Pgd)，而在本算法中对每一维更新后，计算个体历史最优(Pid)和群体全局最优(Pgd)，速度矢量关系如式(9)所示。

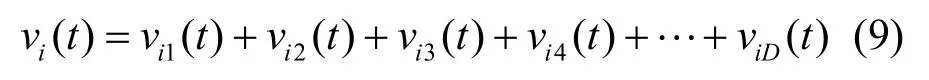
矢量关系图如图1所示。传统的粒子群算法更新时，将 vi(t)看作一个整体，直接从 Xi(t)更新Xi(t+1)。本算法将vi(t)看作各维度之和(如式(9)所示)对每一维的更新过程进行递增搜索，将搜索过程细化，增加了搜索空间，提高了搜索精度。而时间复杂度增量为O(d)，仅与维度有关，与粒子个数n无关，达到以较小的时间代价来提高搜索精度的效果。相对于传统的粒子群算法，时间复杂度提高了O(d)倍，而相对于现有的混沌粒子群算法，时间复杂度降低了M倍，其中，M代表混沌搜索的步长。

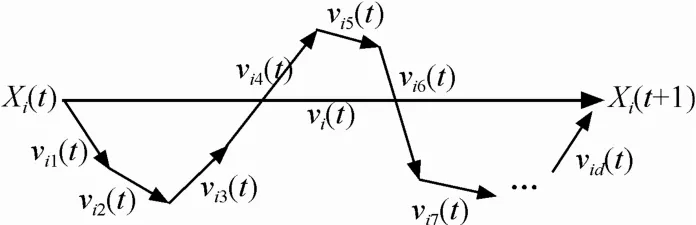
图1 粒子位置更新过程

3.4 混沌与稳定的交替

一直处于混沌或稳定状态对于寻找最优值没有任何意义，只有在混沌与稳定的交替中才能不断向最优结果靠近。也就是说，要在粒子稳定时，引入混沌，跳出局部最优；在粒子不稳定时，加速向最优值靠近，加快收敛过程。

为了定义粒子是否处于稳定状态，引入了2个变量

其中，move表示粒子当前移动距离，stabel表示粒子当前位置与粒子历史上最优值之间的距离。

进一步，将稳定状态条件定义为

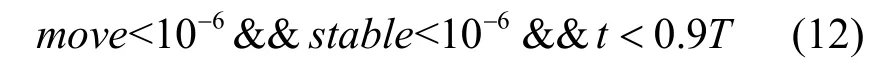
其中，T表示总迭代次数。当粒子移动距离和距离历史最优值较近时，粒子处于稳定状态，此时，令混沌变量Cid(t)=0.999，引入混沌。

当粒子不稳定时，满足条件：

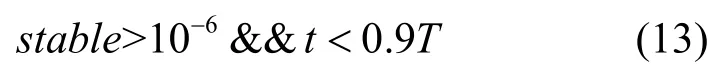
即当粒子移动距离和距离历史最优值较远时，粒子处于运动状态，为了加速收敛过程，令Xid(t)=Pid(t)，保留历史最优值。

4 混沌粒子群算法数值测试

4.1 混沌粒子群模型的非线性动力学行为

为了分析混沌粒子群模型的非线性动力学行为，利用这个优化模型来解决Rastrigin函数优化问题。目标函数如下：

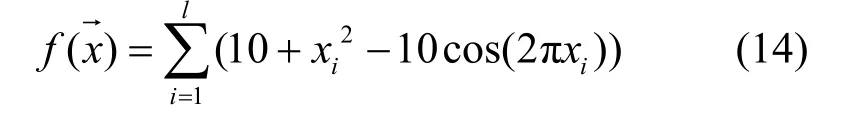
其中，-5.12≤xi≤5.12，l=30，最小值在30维x变量均为0时，全局最小值为0。令混沌粒子群算法中：惯性因子w=0.729 8，学习因子c1=c2=1.496 2，迭代次数为 1 000，粒子个数 N=20，混沌因子r(i,d)=0.5+(0.005)rand，混沌变量初值为 Cid(0)=0.999，搜索测度Ψd=10.24，移动因子Mi=0.5。图2是混沌变量随迭代过程的变化曲线，开始阶段 c(t)由1减为0，是从混沌到粒子群的过程，当粒子群稳定后，c(t)为1，引入混沌跳出局部最优解。

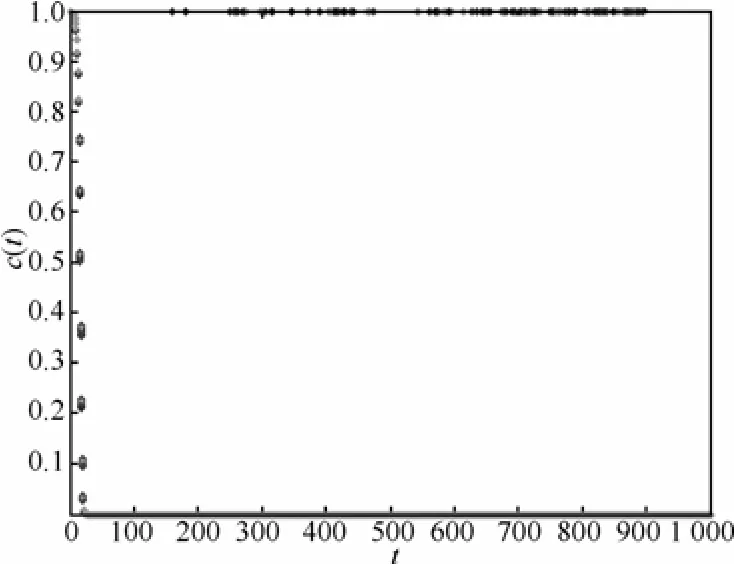
图2 混沌变量随时间变化曲线

图3是粒子1在搜索最优解时X1的变化过程，从图中可以看出，粒子1在对X1的搜索过程中，在稳定和混沌之间交替，并向最优值靠近。图4是所有粒子搜索X1最优值过程，可以观察到整个混沌粒子群也是在混沌与稳定之间交替搜索，跳出局部最优，向全局最优接近。

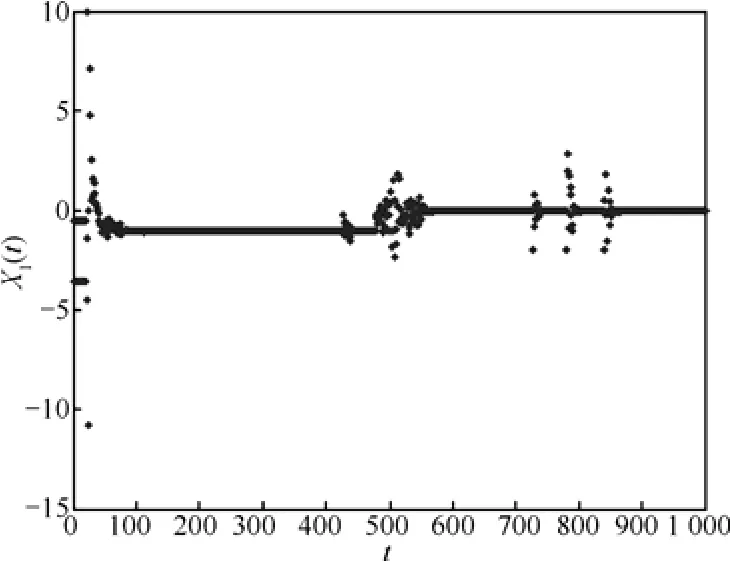
图3 粒子1搜索X1最优值过程

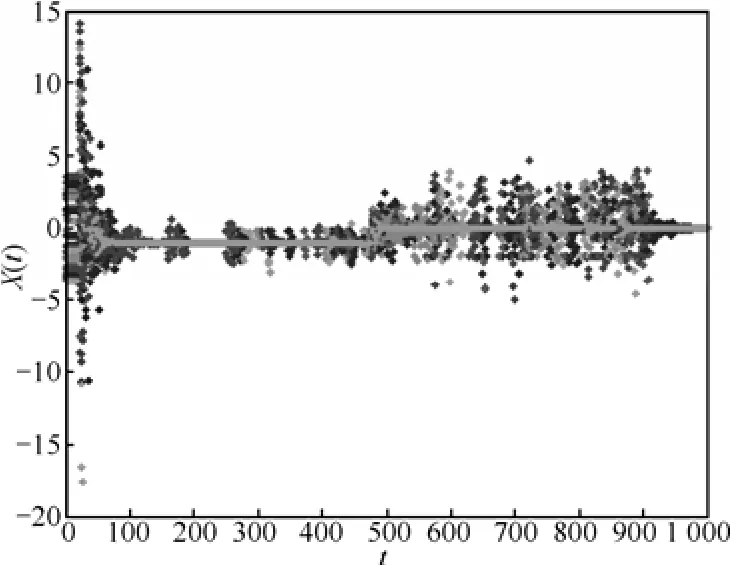
图4 粒子群搜索X1最优值过程

图5 是粒子1的目标函数值变化过程，图6是整个粒子群的目标函数值变化过程。可以看到，粒子的值总体趋势越来越小，但在前0.9T次迭代过程中会有一些起伏的现象，这是因为粒子在混沌的作用下不断在周围探索，以跳离局部最优。在最后0.1T迭代过程中，没有引入混沌，所有粒子在粒子群算法下达到最优状态。

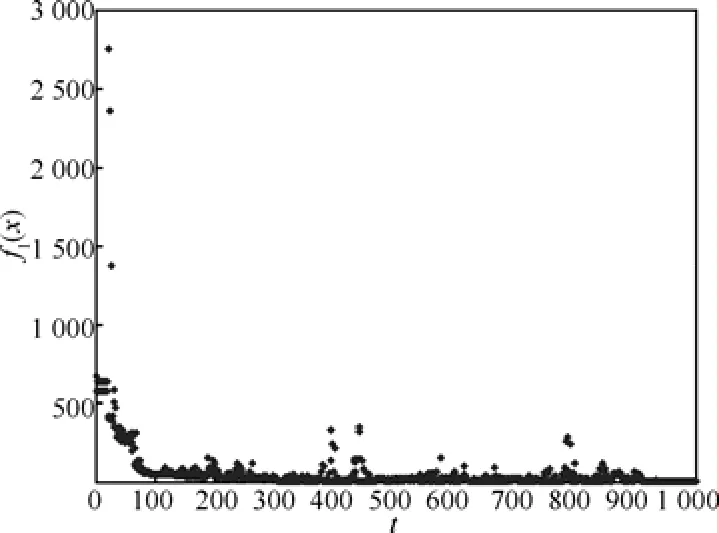
图5 粒子1的目标函数值变化过程

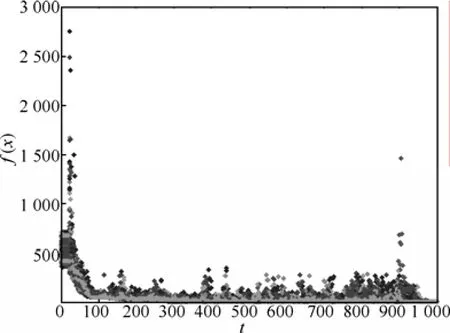
图6 粒子群的目标函数值变化过程

图7 是粒子群的最优值变化过程，随着迭代次数增加，最优值递减。最后得到的优化极值为4.887 8×10-7，各维度的最优位置值均小于1×10-4。

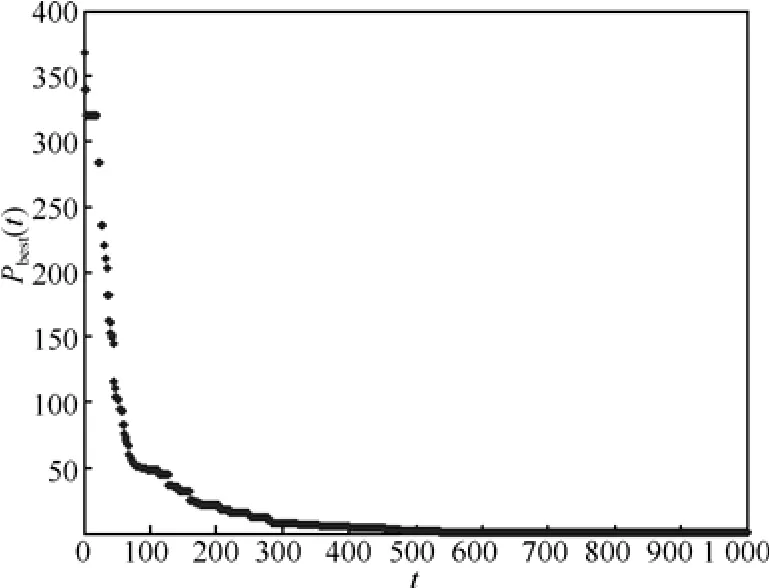
图7 粒子群最优值变化过程

本算法的参数中，惯性因子w、学习因子可根据粒子群算法最优来设置，搜索测度、移动因子可根据初始搜索条件进行计算得出，混沌变量初值为Cid(0)=0.999，比较重要的参数是混沌因子的大小，它影响了初始混沌搜索的时间，下面令混沌因子为：r(i,d)=0.1+(0.001)rand进行数值仿真，说明混沌因子参数对该算法搜索过程的影响。

图 8是混沌变量随时间变化曲线，图 9和图10分别是单个粒子、粒子群对变量X1的搜索过程，图11和图12分别给出了单个粒子、粒子群的能量函数时间演化，图13给出了整个粒子群最优值的变化过程。通过对比图8～图13与图2～图7，可以看出混沌因子对算法搜索过程的影响，初始混沌搜索过程由原来的20次迭代变为100次迭代。混沌因子 r(i,d)越小，混沌变量减小的过程越慢，混沌搜索时间越长，有利于搜索到较优值，但初始混沌收敛过程越长。最后得到的优化极值为1.388 50×10-7，各维度的最优位置值均小于1×10-4。

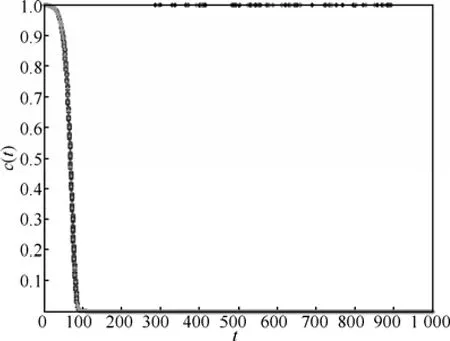
图8 混沌变量随时间变化曲线

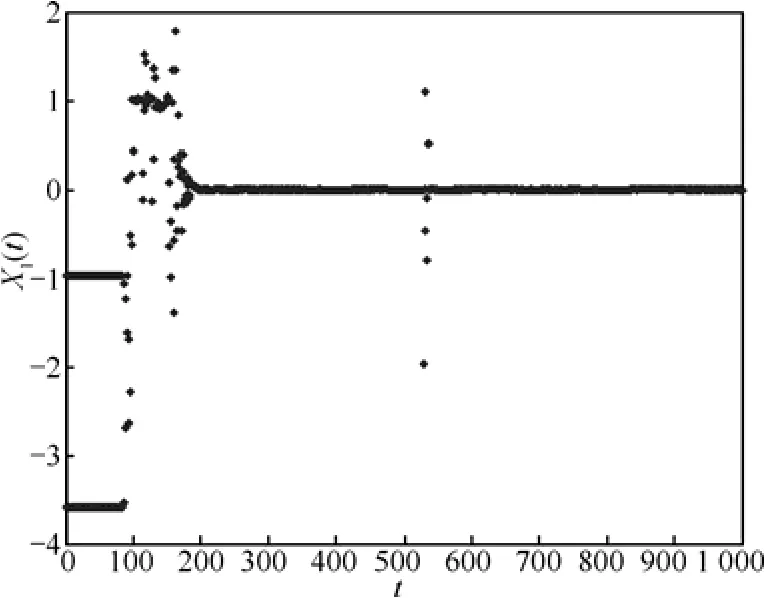
图9 粒子1搜索X1最优值过程

图10 粒子群搜索X1最优值过程

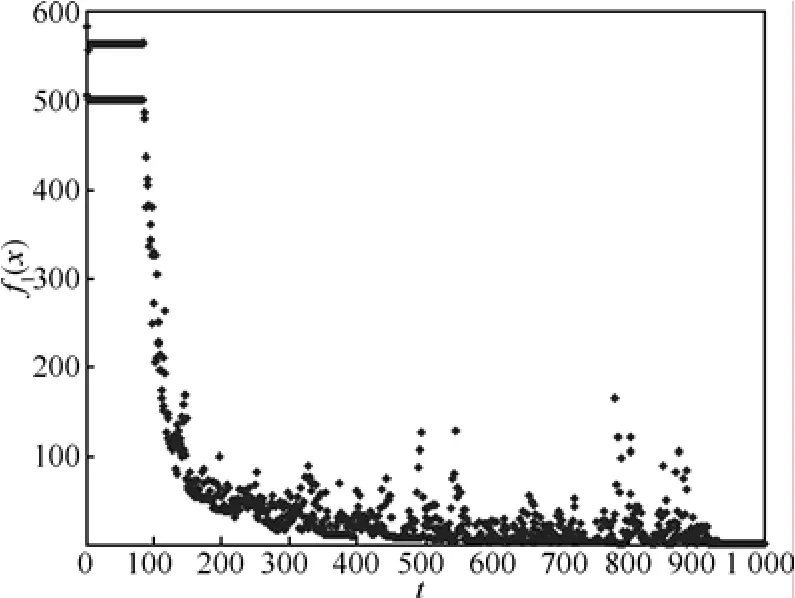
图11 粒子1的目标函数值变化过程

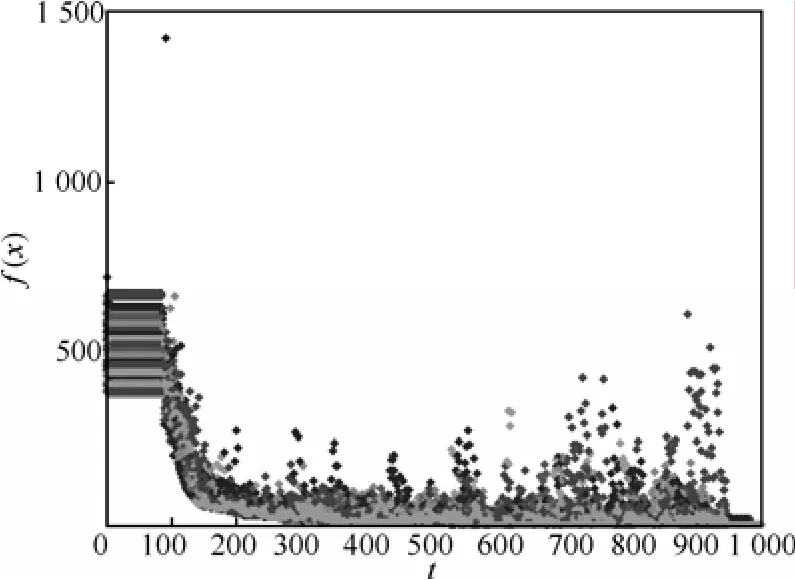
图12 粒子群的目标函数值变化过程

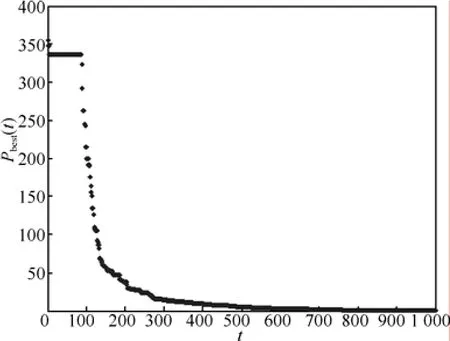
图13 粒子群最优值变化过程

4.2 算法性能数值测试

为了检测混沌粒子群算法的性能，选取5个测试函数进行测试，它们是在进化规划、模拟退火、遗传算法和粒子群优化中广泛使用的数值测试函数，分别如下。

Sphere 函数：

其中，-50≤xi≤50，其全局最优点在 X=(0,0,0,…,0)，全局极值为0。

DeJong函数：

其中，-20≤xi≤20，其全局最优点在 X=(0,0,0,…,0)，全局极值为0。

Griewank 函数：

其中，-600≤xi≤600，其全局最优点在X= (0,0,0,…,0)，

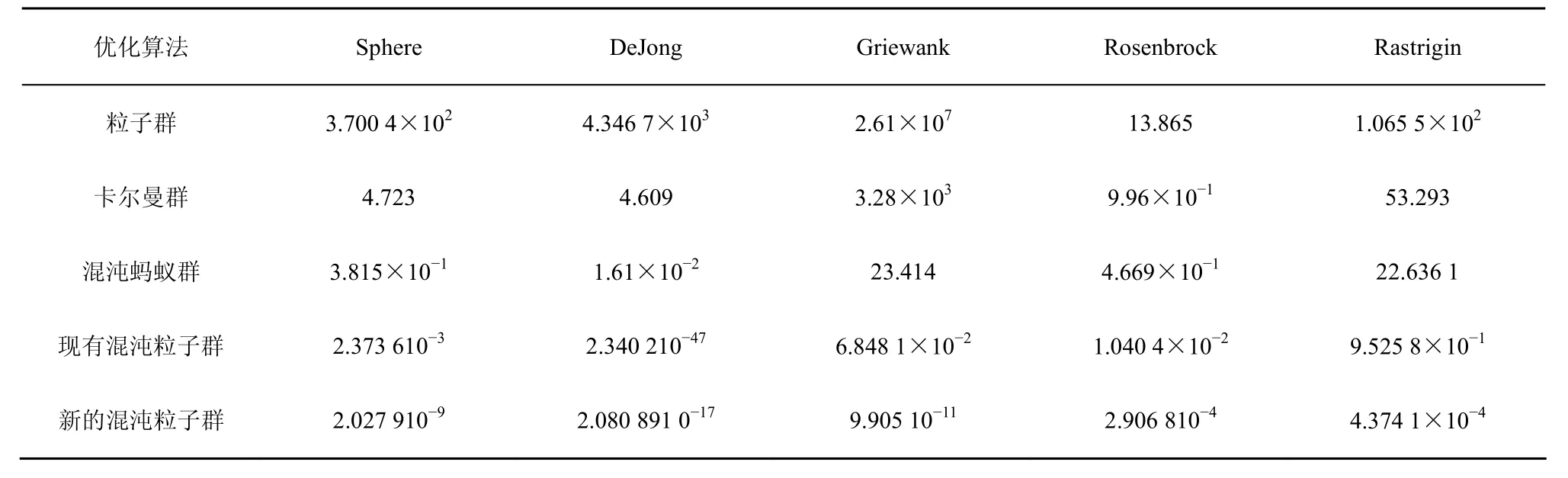
表1 数值测试结果

全局极值为0。

Rosenbrock 函数：

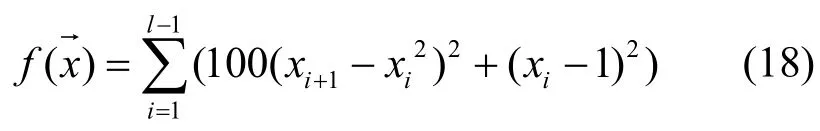
其中，-100≤xi≤100，其全局最优点在 X=(1,1,1,…,1)，全局极值为0。

Rastrigin函数：

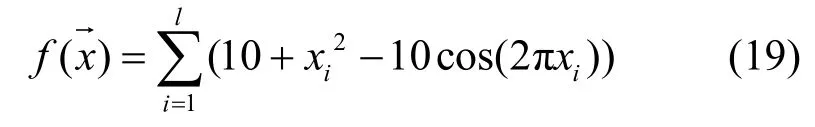
其中，-5.12≤xi≤5.12，其全局最优点在X=(0,0,0,…,0)，全局极值为0。

混沌粒子群参数设置为：w=0.729 8，c1=c2=1.496 2，T=1 000，r(i,d)=0.5+(0.005)rand，N=20，Cid(t)=0.999，Ψd为各自搜索空间长度，Mi=0.5，粒子初始值为 Ψd×Mi×(2rand()-1)。现有的粒子群算法实验采用logistic混沌模型，最大迭代步长为15。在维度l=30的情况下，进行50次测试取平均值的结果如表1所示，其他算法结果来自文献[15]。

对比表1中的结果可以看出，本文所提出的混沌粒子群算法测试结果明显好于粒子群、卡尔曼群、混沌蚂蚁群、现有混沌粒子群的测试结果，搜索精度至少提升了100倍。

图14～图18为现有混沌粒子群算法与本文提出的混沌粒子群算法对5个标准测试函数进行优化的过程中，种群最优值进化曲线的对比。可以看出，相对于现有的混沌粒子群算法，本文提出的混沌粒子群在经过若干代运算之后仍保持较高的活性，可以从局部最优中跳离出来，保持较快的收敛速度，极大地提高了对最优值的全局搜索能力。

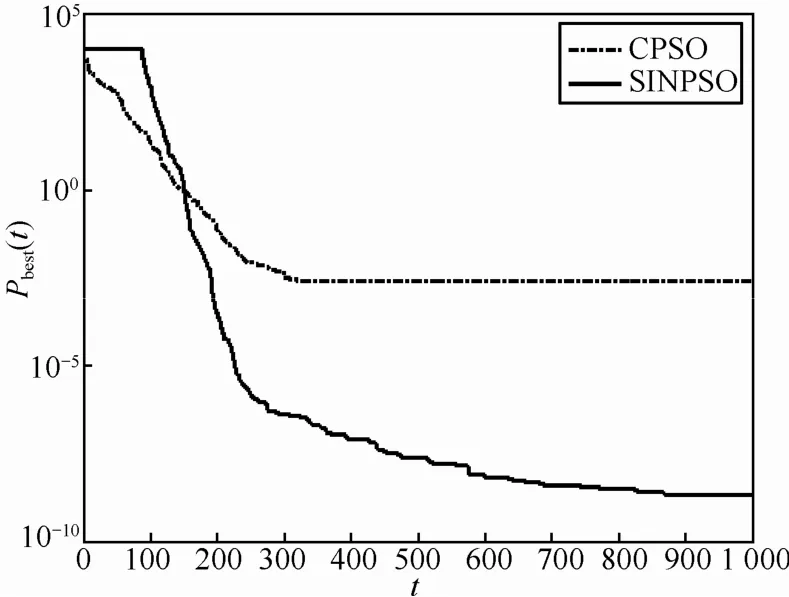
图14 Sphere函数寻优过程

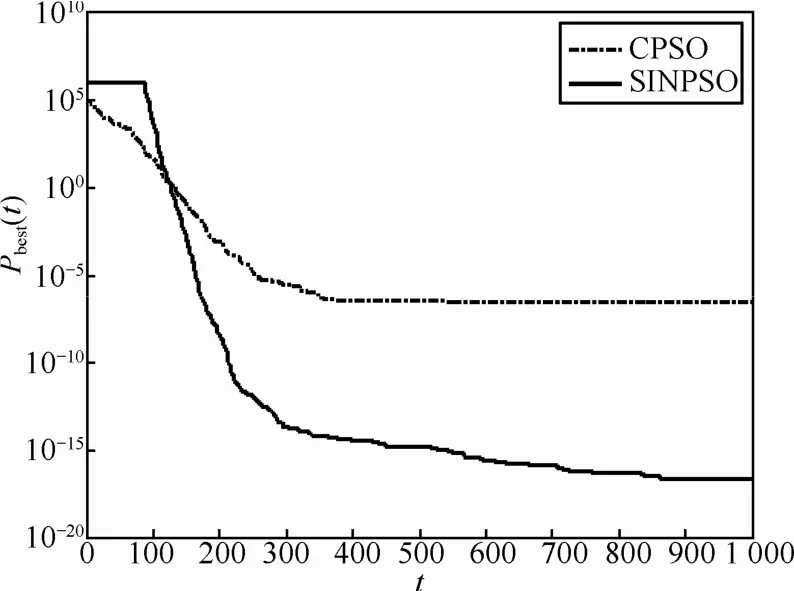
图15 DeJong函数寻优过程

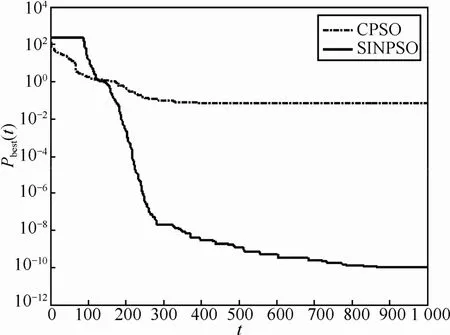
图16 Griewank函数寻优过程

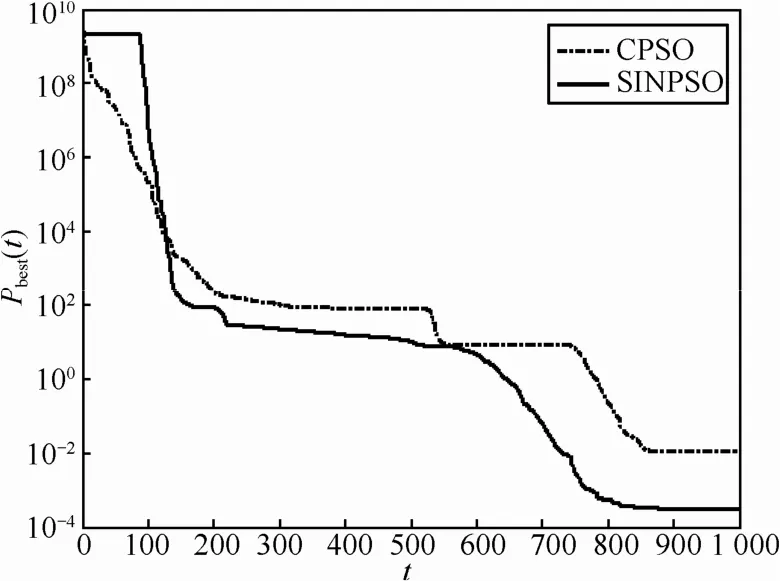
图17 Rosenbrock函数寻优过程

图18 Rastrigin函数寻优过程

5 结束语

本文利用混沌的遍历性和粒子群收敛快的特点，提出了一种新的混沌粒子群算法。该算法将混沌融入到粒子运动过程中，不同于己有的混沌粒子群算法的简单粒子序列替换，使粒子群在混沌与稳定之间交替向最优点靠近，并提出了一种新的混沌粒子群数学模型。本文还给出了混沌粒子群算法的非线性动力学行为分析，并和目前国际上流行的算法，如粒子群算法、卡尔曼群算法、混沌蚁群算法和现有混沌粒子群算法作了对比分析。文中给出的数值结果表明该方法用于解决函数最优化问题的有效性，并且能有效避免粒子群优化算法的早熟收敛问题，能跳出局部最优，极大提高了计算精度和全局寻优能力。

[1] KENNEDY J, EBERHART R C. Particle swarm optimization[A]. Proc of the First IEEE International Conference on Neural Networks[C].Perth, Australia：IEEE Press, 1995. 1942-1948.

[2] MODARES H, ALFI A, NAGHIBI-SISTANI M B. Parameter estimation of bilinear systems based on an adaptive particle swarm optimization[J]. Engineering Applications of Artificial Intelligence, 2010, 23(7):1105-1111.

[3] KARAKUZU C. Parameter tuning of fuzzy sliding mode controller using particle swarm optimization[J]. International Journal of Innovative Computing, Information and Control, 2010, 6(10):4755-4770.

[4] KULKARNI R V, VENAYAGAMOORTHY G K. Bio-inspired algorithms for autonomous deployment and localization of sensor nodes[J].IEEE Transactions on Systems, Man, and Cybernetics, 2010, 40(6):663-675.

[5] ZHANG W, LIU J, NIU Y Q. Quantitative prediction of MHC-II binding affinity using particle swarm optimization[J]. Artificial Intelligence in Medicine,2010,50(2):127-132.

[6] GHEITANCHI S, ALI F, STIPIDIS E. Particle swarm optimization for adaptive resource allocation in communication networks[J]. EURASIP Journal on Wireless Communications and Networking, 2010. 1-13.

[7] BERGH F. An Analysis of Particle Swarm Optimizers[D]. Department of Computer Science, University of Pretoria, South Africa, 2006.118-123.

[8] JIAO B, LIAN Z G, GU X S. A dynamic inertia weight particle swarm optimization algorithm[J]. Chaos, Solitons & Fractals, 2008, 37(3):698-705.

[9] MENG H J, ZHENG P, WU R Y, et al. A hybrid particle swarm algorithm with embedded chaotic search[A]. Proceedings of the 2004 IEEE Conference on Cybernetics and Intelligent Systems[C]. Singapore, 2004. 367-371.

[10] XIANG T, LIAO X F, WONG K. An improved particle swarm optimization algorithm combined with piecewise linear chaotic map[J].Applied Mathematics and Computation, 2007,190(2): 1637-1645

[11] ALATAS B, AKIN E, OZER A B. Chaos embedded particle swarm optimization algorithms[J]. Chaos Solitons & fractals, 2009, 40(4):1715-1734.

[12] COELHO L D, MARIANI V C. A novel chaotic particle swarm optimization approach using Henon map and implicit filtering local search for economic load dispatch[J]. Chaos Solitons & Fractals, 2009,39(2):510-518.

[13] ZHANG Y D, JUN Y, WEI G, et al. Find multi-objective paths in stochastic networks via chaotic immune PSO[J]. Expert Systems With Applications, 2010, 37(3): 1911-1919.

[14] 高飞, 童恒庆. 基于改进粒子群优化算法的混沌系统参数估计方法[J]. 物理学报, 2006, 55(2): 577-582.GAO F, TONG H Q. Parameter estimation for system based on particle swarm optimization[J]. Acta Phys, 2006, 55(2):577-582.

[15] LI L X, PENG H P, WANG X D, et al. An optimization method inspired by chaotic ant behavior[J]. International Journal of Bifurcation and Chaos, 2006, (16): 2351-2364.

[16] SOLE R V, MIRAMONTES O, GOODWIN B C. Oscillations and chaos in ant societies[J]. Journal of Theoretical Biology, 1993,161(3): 343-357.