位似曲线与单参数曲线族

钱季伟

（长江工程职业技术学院，武汉 430212）

在中学数学中，用内角的相等或边长的成比例来定义三角形或多边形的相似，显然这种方法不能推广到曲线（形）上来，因此必须挖掘相似性的更本质的内涵，使之可以在更广泛的场合下应用于相似问题的讨论。

1 若干定义

（1）位似变换。取定平面上一点O，称为位似中心，规定点O在位似变换下的象即自己；平面上其他的点p在变换下的象p＇满足：p＇在直线op上，＝k（≠0.1），k称为位似比，p称为p＇的原象。显然象与原象的概念是对称的，若以p＇为原象，点p为象，则位似比

在直角坐标系中，以原点O为位似中心，位似变换可表示为：

图1

（2）对平面上任意曲线F上所有的点作位似变换，所有的点的象组成曲线F＇，则称F＇与线F是位似曲线。

（3）对于曲线G与G＇，若能通过平面上的等距（平移、旋转与反射）变换，使之成为位似曲线，则称G与G＇为相似曲线。

由以上定义可知：两曲线是相似的，必须且只须它们是位似的；曲线的位似是曲线相似的本质的表示形式，因此位似比也可称为相似比。

2 引 理

以坐标原点O为位似中心，k为位似比，若曲线C1的方程为Φ（x，y）＝0，则曲线C2是C1的位似曲线的充分必要条件是：它的方程是（考虑到几何图形的清晰性，规定曲线与以位似中心为始点的射线最多相交于一点。）

证：对C1上所有的点P（x，y），作变换（1），即以代入 Φ（x，y）＝0，得到曲线Φ该曲线上的点P＇（x＇，y＇）是C1上的点P 的象，且，所以是C1的位似比为k的位似曲线。再把x＇，y＇改写为x，y，就得到位似曲线的方程：

由此可知，具有方程（2）的曲线C2确是C1的位似曲线，这就证明了条件的充分性；因为对于确定的k，曲线C1的位似曲线是唯一的，所以方程（2）也是必要的。

例1：① 以p为参数的抛物线族y2＝2px（p＞0）中的任意两抛物线y2＝2p1x，y2＝2p2x是位似曲线。

②任意两抛物线是相似曲线（不论其解析式如何）。

② 对于任意两抛物线C1与C2，我们总可以通过适当的等距变换，使它们的方程成为：

（确切地说，把C1、C2变换到顶点在原点，以X轴为对称抽，开口向右）此时，因为抛物线y2＝2p1x，y2＝2p2x是位似曲线，根据定义，C1与C2是相似曲线。

3 定 义

若单参数的曲线族F（x，y，s）＝0中的任意两曲线F（x，y，s1）＝0，F（x，y，s2）＝0是位似曲线，则称F（x，y，s）＝0是位似曲线族。

由本例知道，以p为单参数的抛物线族y2＝2px是位似曲线族，但是并非所有单参数的曲线族都是位似曲线族，例如：椭圆族中的任意两椭圆都不是位似曲线，实际上椭圆族中所有椭圆都相交于点（0，1）和（0，-1）两点，所以它不是位似曲线族。

对于一个单参数曲线族f（x，y，s）＝0，如何判定它是位似曲线族，即它的任意两曲线都是位似曲线，我们有如下的定理：

在以坐标原点O为位似中心的坐标系中，以s为参数的单参数曲线族f（x，y，s）＝0是位似曲线族的充分必要条件是：设f（x，y，s1）＝0，f（x，y，s2）＝0是曲线族中任意两条曲线，若存在与s1，s2有关的常数k，使方程f（x，y，s2）＝0能等价地变换为方程

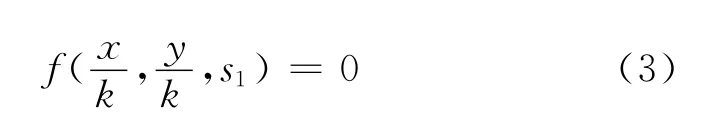
则该曲线族是位似曲线族。

根据引理，曲线f（x，y，s1）＝0，f（x，y，s2）＝0是位似曲线，又因为s1，s2是任意的，所以，以s为参数的单参数曲线族f（x，y，s）＝0是位似曲线族。

4 相似（位似）曲线的性质

虽然有各类不同的相似（位似）曲线，但是不同种类的相似（位似）曲线却有着共同的性质，例如相似（位似）比为k的两相似（位似）曲线有以下性质：

① 对应弧段（对应弦）的长度之比等于k；② 以对应弧段为曲边的曲边三角形的面积之比等于k2；③对应点的曲率之比等于

证：在以坐标原点O为位似中心的坐标系中，设曲线C1的方程为y＝φ（x），则根据引理，方程为的曲线C2是C1的位似曲线，C1上的点为原象，位似比为k（如图2所示）。

图2

设点P1和P2的x坐标为x1和x2，则对应的点（即其象）Q1和Q2的x坐标是kx1和kx2，

于是弧段P1P2的长度

5 相似三角形（多边形）的位似

回顾本文的开始，由于定义三角形（多边形）的方法不能推广到曲线的情况，于是引入位似变换，给出了曲线位似和相似的定义。显然，这个推广了的定义，应该把三角形（多边形）也包括进去。下面给予验证。

图3

如图3，令AB‖A＇B＇，AC‖A＇C＇，BC‖B＇C＇。

证：① 若 P，P＇在AB，A＇B＇上，（或在 AC，A＇C＇上），则因为三角形OAP与三角形OA＇P＇相似，所以

② 若P，P＇在BC，B＇C＇上，则因为三角形OPD与三角形OP＇D＇相似，所以注意三角形ABD 与三角形A＇B＇D＇相似，所以于是

以上我们证明了相似三角形任意一组对应边上任意两个对应的点P，P′，存在所以点O是位似中心，相似的三角形也是位似形，相似比k就是位似比。

6 位似曲线方程不唯一

最后有必要作一点说明：以坐标原点为位似中心，一组（两条）位似曲线可以因其与位似中心的不同位置关系而得到不同形式的方程，例如：对称轴为x轴，开口向右的抛物线，以顶点为位似中心的方程为y2＝2pix（px＞0，i＝1，2），以焦点为位似中心的方程为