全站仪三维坐标测量在道路中、边桩及高程测量中的应用

罗 勇，牛志宏

（长江工程职业技术学院，武汉 430212）

在道路工程的施工过程中，经常涉及到道路中、边线放样及路基高程测量。传统的测量方法是先用全站仪定出道路的中线，然后用钢尺量出道路的边线，再用水准仪根据道路的坡度进行高程测量。这种方法为多数施工单位所使用，但是各测量过程必须分步进行，在机械化铺路过程中效率显得有些低下，笔者根据全站仪测量功能的特点，结合工程施工测量经验，总结出一种利用全站仪进行道路中、边线放样及高程测量的快速方法，该方法将中、边桩放样及高程测量融为一体，在一站上就可以完成中、边桩放样和高程测量，大大提高了放样测量的工作效率。

1 全站仪任意设站三角高程测量原理

如图1所示传统的三角高程测量是将仪器安置在已知点A上，A点高程HA为已知，若知道A点与B点之间的高差HAB，即可由HB＝HA＋HAB得到B点的高程HB，即

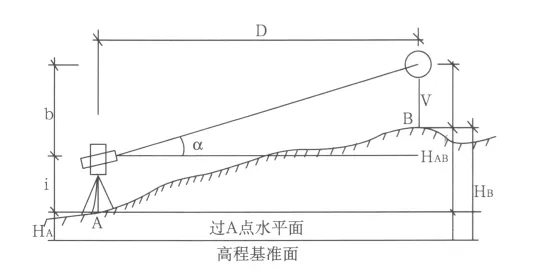
图1 三角高程测量示意图

如果利用全站仪任意设置测站点的功能，同时又不用量取仪器高和棱镜高的情况下，利用三角高程测量原理测出待测点的高程，那么将大大提高高程测量的速度。如图1，假设B点的高程为已知，A点的高程为未知，要通过全站仪测定其它未知点的高程。首先由（1）式可知：

（2）式中，除Dtanα，即图1中的b值可以用全站仪直接测出外，i、v都为未知量。但是，仪器一旦安置好，i值也将随之固定不变，同时，所选假定棱镜杆高度固定不变，即v值固定不变。则从（2）式可得：

由（3）式可得，基于上面的假设，若仪器在任意站上固定，则HA＋i-v的值固定不变，且可根据HB的值计算出P值。

该方法的操作步骤如下：

（1）将仪器安置在任意点上，所选点位要求能和已知高程点通视。

（2）用仪器照准已知高程点，测出b值，并算出P值。（此时与仪器高程测定有关的常数如测站点高程，仪器高，棱镜高均为任意值，施测前不必设定。）

（3）将仪器测站点高程重新设定为P，仪器高和棱镜高设为0即可（在求出P值后仪器中的i和v都不能变化）。

（4）照准未知点测出其高程。

下面从理论上分析这种方法的正确性。

综合（1）、（3）两式

上式中：H′B为待测点的高程；P为测站中设定的测站点高程；D′为测站点到待测点的水平距离；α′为测站点到待测点的观测垂角。从（4）式可知，不同未知点的高程随着测站点到其水平距离或观测垂直角的变化而改变。

将（3）式代入（4）式可知：

由三角高程测量原理可知

将（3）式代入（6）式可得：

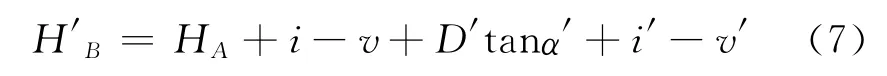
这里i′、v′为0，所以：

由（5）式和（8）式可知，两种方法测出的未知点的高程在理论上是一致的。而且整个过程不必用钢尺量取仪器高、棱镜高，测出的结果从理论上分析比传统的三角高程测量精度更高，因为它减少了误差来源。同时需要指出的是，在实际测量中，棱镜高还可以根据实际情况改变，只要记录下相对于初值v增大或减小的数值，就可在测量的基础上计算出待测点的实际高程。

2 全站仪中、边桩放样测量

2.1 放样测量坐标系的建立

在道路中、边桩放样中，我们习惯于根据道路的走向建立一个施工独立坐标系（如图2）。该坐标系的原点位于该道路中桩的起点上，且在道路中桩的大里程方向上方位角为0°，小里程方向上方位角为180°。这样我们就可以得知，在道路左边的路宽值为负值，右边的路宽值为正值。

图2 施工独立坐标系

2.2 放样测量操作程序

（1）利用全站仪坐标放样定出两个相互通视的道路中桩。假设放样两中桩分别为：K2＋100，K2＋300。

（2）将全站仪架设在其中任一中桩上，若架设中桩点号为K2＋100，以K2＋300为后视，并将其水平角设置为0°。

（3）进入全站仪三维坐标测量模式，将测站设置为N∶2100、E∶0、H∶0。瞄准一高程控制点进行测量（假设该控制点高程为HC），可得出仪器中心与棱镜中心之间的高差Δh，根据新三角高程测量原理，可得出仪器中心的高程H2100＝HC-Δh。将测站重新设置为：N∶2100、E∶0、H∶H2100。

（4）设置完毕后可以进行任意点的测量，仪器显示值为该道路坐标系中的坐标值。

综上所述，利用上述方法进行道路施工放样，可以使平面放样和高程测量一同进行，经过精度分析，高程测量精度可达到四等水准要求，中边桩放样精度优于普通钢尺量距，大大提高了测量的精度和效率。