单层洞桩法暗挖车站边桩结构受力及变形特征研究

孙玉辉 张子真 陈昌彦 王金明

(北京市勘察设计研究院有限公司，100038，北京∥第一作者，高级工程师)

目前，对于传统洞桩法(双层导洞)暗挖车站，一般采用理论分析和经验类比相结合的设计方法,而对于新型单层洞桩法车站结构受力体系，几乎未见相关研究。边桩作为单层洞桩法暗挖车站施工期间(在车站主体拱、墙、板完成之后就不再将其作为受力构件考虑)承担竖向荷载及侧向土压力的构件，是该施工方法的重要组成部分，对于其结构受力体系及变形特征，缺乏理论研究和现场实测验证。基于此，在单层洞桩法暗挖施工中，对边桩桩顶压力、钢筋应力、混凝土应变，以及边桩顶竖向位移、桩身水平位移等进行监测，通过数据分析并结合理论分析总结出单层洞桩法施工过程中边桩的结构受力体系，为设计、理论研究提供参考及真实数据支撑。

1 工程概况

北京地铁某地铁车站暗挖段为地下二层双柱三跨连拱直墙结构，采用暗挖洞桩法施工，结构覆土厚度为14.00 m，结构总高度为17.12 m。边桩直径为1.00 m，桩中心距为1.25 m；中柱桩基直径为1.80 m，桩中心距为7.00 m。车站底板以下为卵石⑨层，边桩和中柱桩基嵌固深度分别为12.00 m、17.80 m。

地层以人工填土层、粉质黏土、黏质粉土等交互地层为主，拱顶为砂卵地层，局部为粉细砂地层，车站结构范围内为砂卵地层，存在层间潜水，底板位于砂卵地层、隔水层以上。具体车站结构断面及地层如图1所示。

图1 车站结构断面及地层剖面图

2 监测方案设计

本次监测项目主要为边桩顶压力、边桩钢筋应力、边桩混凝土应变、边桩顶竖向位移、边桩水平位移等。各监测项目尽量布设在同一断面上，便于各种监测数据的综合分析与相互验证。具体监测点布设位置如图2所示。监测方法及仪器精度如表1所示。

表1 监测方法、仪器精度及测点布设统计表

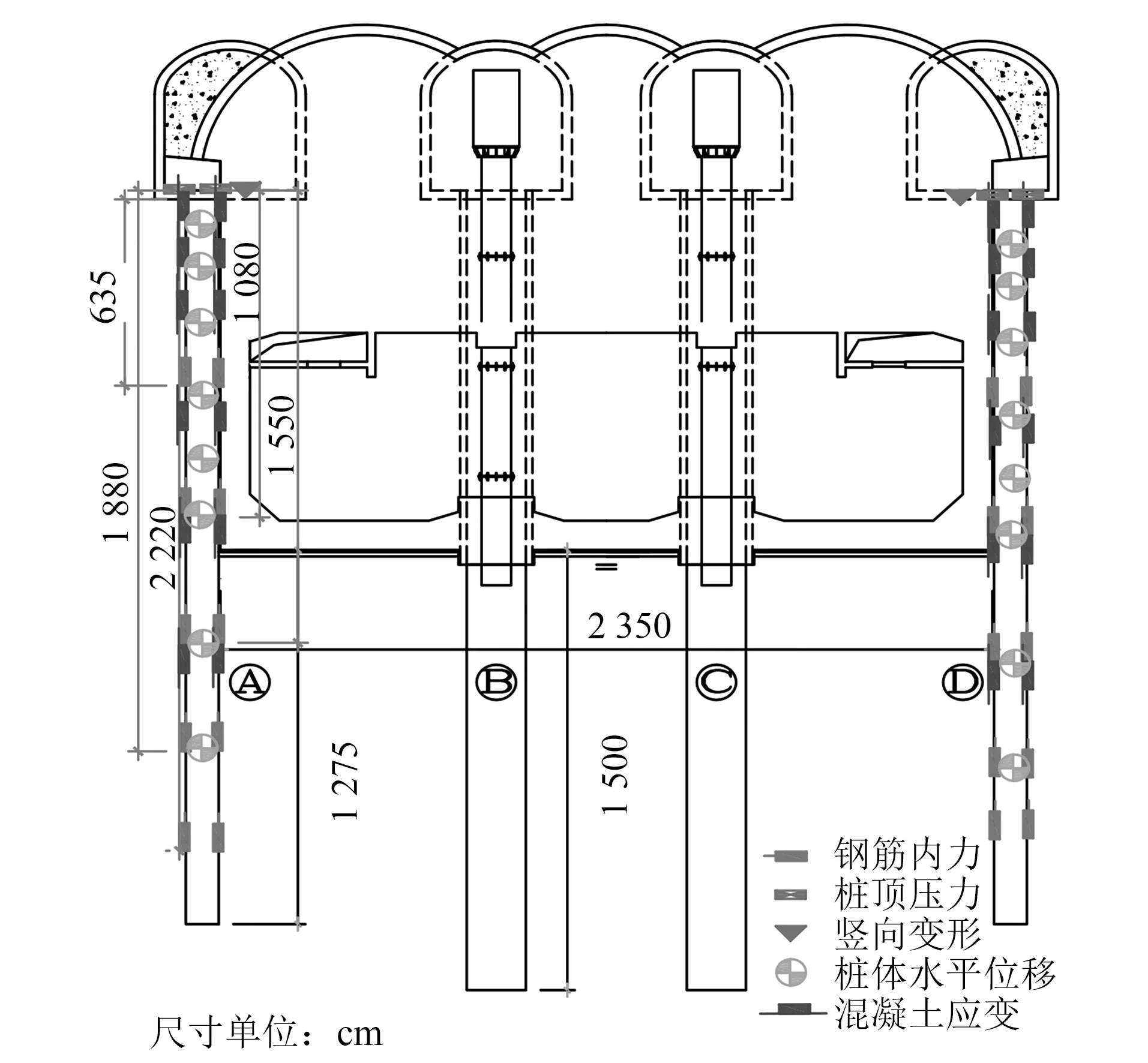
图2 监测布设位置剖面图

3 结构受力及变形特征

3.1 边桩顶压力

共对6根边桩布设了桩顶压力监测装置，监测数据总结分析如表2所示。特殊监测点变形时程曲线如图3所示。

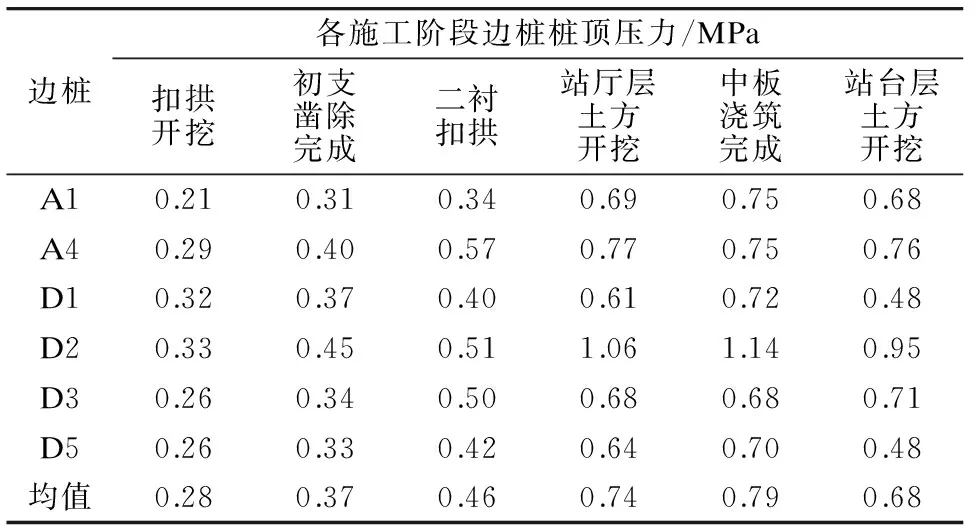
表2 不同边桩各施工阶段的桩顶压力监测值

图3 不同施工阶段A4边桩桩顶压力变形时程曲线

由表2和图3可看出：

1) 桩顶压力变形主要发生在初支扣拱、二衬扣拱、站厅层土方开挖阶段，各施工阶段桩顶压力变形量占总变形量的比例分别为35%、22%、36%。桩顶压力最大值出现在站厅层土方开挖完成后，范围为0.68～1.14 MPa之间，平均值为0.79 MPa，根据边桩直径换算成荷载为620.15 kN。

边桩顶部荷载q计算公式为：

q=(γ1h1+γ2h2)LB

(1)

式中：

γ1——顶板以上土层重度加权平均值，根据地层参数计算，其值为19.50 kN/m3；

γ2——结构所在土层重度加权平均值，根据地层及结构参数计算，其值为20.70 kN/m3；

L——边桩影响的长度，根据地层及结构参数计算，其值为1.25 m；

B——边桩影响的宽度，根据地层及结构参数计算，其值为6.00 m；

h——边桩影响的高度,根据地层及结构参数计算，h1、h2取值均为6.00 m。

根据式(1)，理论计算中板完成后边桩顶荷载为3 553.43 kN(按照全土柱法，覆土厚度为14 m，如果根据拱顶压力监测数据反推的松散围岩高度为3.5 m，则计算荷载为2 017.8 kN)。理论计算值远大于现场实测值620.15 kN(根据实测边桩桩顶压力及边桩直径换算所得)，可解释为荷载由边桩背后土体及导洞初支分担。

2) 边桩压力变形规律原因分析。

(1) 冠梁及假拱施做期间对桩顶压力影响较小，荷载沿小导洞初支直接向下传递到导洞底板地层处，桩顶及冠梁在导洞初支底板之上，受力较小。

(2) 初支扣拱期间，扣拱导洞土方开挖后围岩应力作用在格栅上，并随着开挖掌子面的推进，拱顶受覆土压力开始向两边传递到拱脚并由边桩承担。

(3) 二衬扣拱期间，初支凿除后原拱顶荷载由导洞及大拱初支共同承担，变为由初支大拱单独承担并沿格栅传递拱脚，最终由边桩承担。

(4) 站厅站台土方开挖过程中，侧墙及中板结构自重均有边桩承担，直到二衬框架结构完全完成。

3) 扣拱掌子面与边桩距离对边桩顶压力变形的影响范围如图4所示。从图4中可以看出：边桩距离扣拱掌子面前10 m，桩顶压力开始出现增长变化；扣拱掌子面通过该桩30 m后，桩顶压力出现平稳趋势。扣拱开挖对边桩顶压力的影响范围是-10 m～30 m。

图4 扣拱掌子面与边桩距离对边桩顶压力变形的影响范围

3.2 边桩钢筋内力

各工序节点边桩钢筋内力值统计如表3所示。典型测点时程曲线如图5～6所示。

表3 各工序节点不同施工阶段边桩钢筋内力值

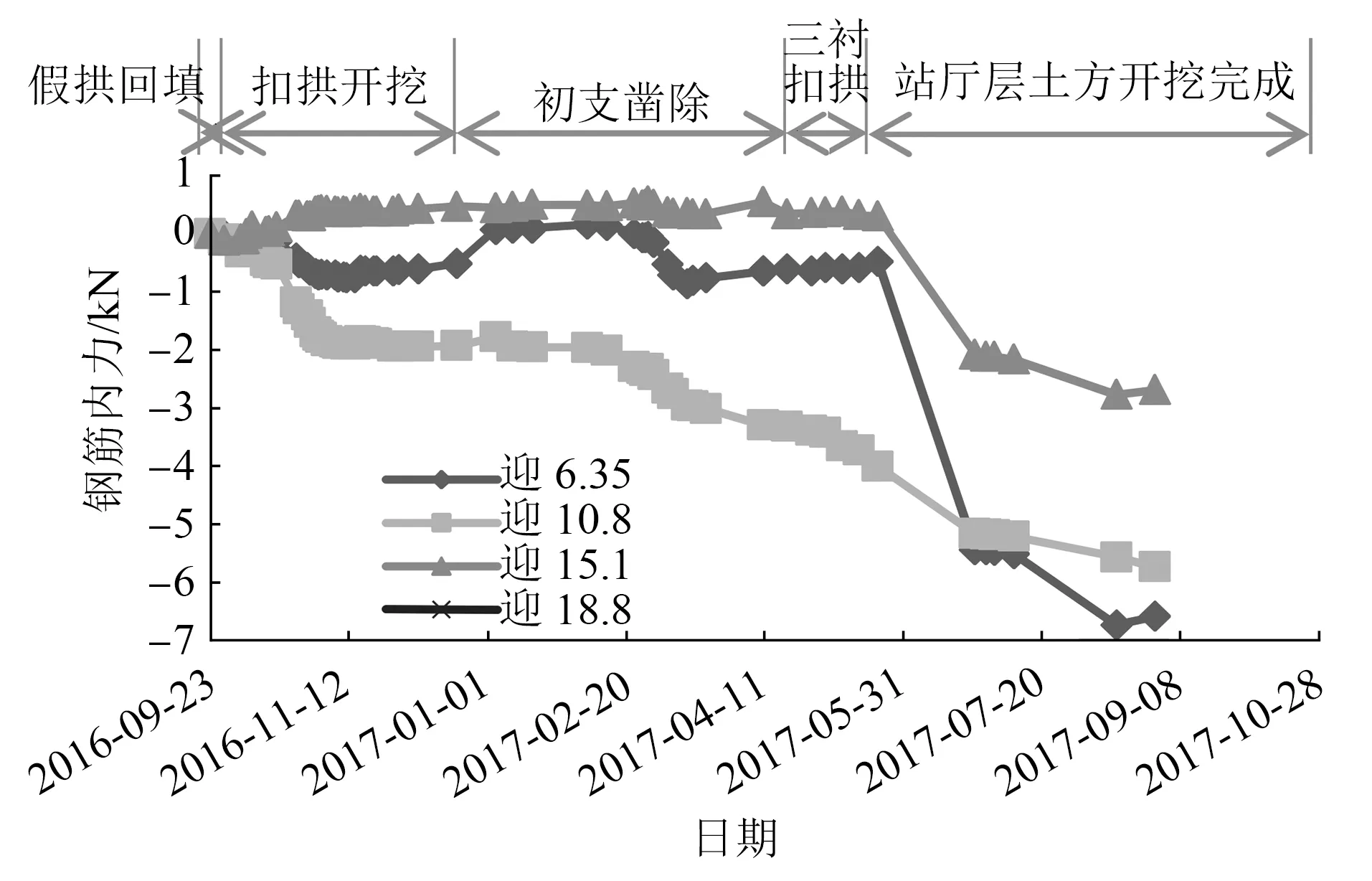
图5 不同施工阶段迎土侧边桩钢筋内力时程曲线

图6 不同施工阶段背土侧边桩钢筋内力时程曲线

由表3及图5～6可得：

1) 钢筋内力变形主要发生在初支扣拱、二衬扣拱、土方开挖三个阶段。其中：初支扣拱和二衬扣拱阶段变形规律同桩顶压力变形规律；土方开挖阶段由于迎土侧土侧压力造成桩身向车站侧发生变形，钢筋应力也急剧增加，并且均呈受压状态。

2) 由于土方开挖边桩侧摩阻力减少，致使桩轴力向下传递更深(桩深部的轴力急剧增加)，增加的轴力由底板以下桩侧阻力承担。

3.3 边桩混凝土应变

各工序节点边桩混凝土应变值统计如表4所示。典型测点时程曲线如图7～8所示。

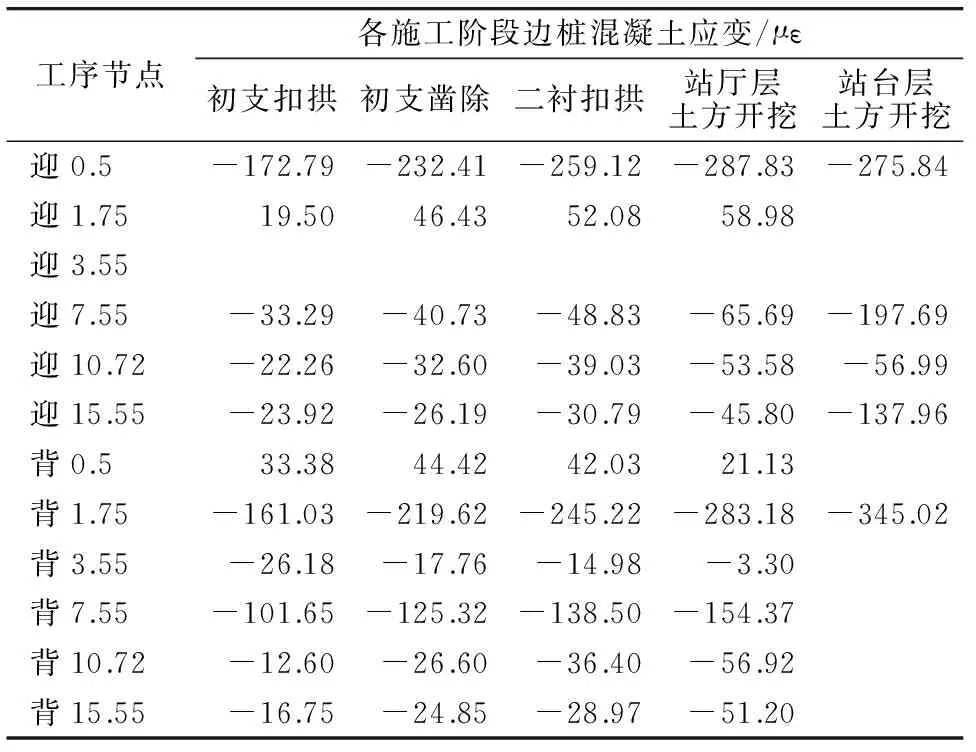
表4 各工序节点不同施工阶段边桩混凝土应变值

图7 不同施工阶段迎土侧边桩混凝土应变时程曲线

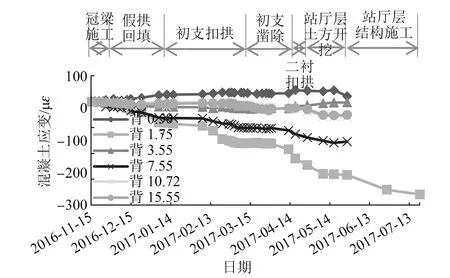
图8 不同施工阶段背土侧边桩混凝土应变时程曲线

由表4及图7～8可知，边桩混凝土应变变化规律与边桩钢筋内力的相同。

边桩轴力F计算公式为：

ε轴=(ε迎土侧+ε背土侧)/2

(2)

F=EcAε轴

(3)

式中：

ε轴——边桩混凝土应变；

ε迎土侧——边桩混凝土迎土侧应变；

ε背土侧——边桩混凝土背土侧应变；

Ec——混凝土强度(C30取值30 000 N/mm2)；

A——边桩截面积。

不同边桩深度的轴力计算结果如表5所示。

表5 不同边桩深度各施工阶段轴力值

边桩侧摩阻力qs计算公式为：

qs=ΔFN/(liμp)

(4)

式中：

ΔFN——相邻两个监测点轴力差；

li——相邻两个监测点距离；

μp——桩截面周长。

不同边桩深度的侧摩阻力计算结果如表6所示。

表6 不同边桩深度各施工阶段侧摩阻力值

由表5～6可知：

1) 桩身混凝土应变整体呈受压状态，根据式(2)、式(3)和式(4)，利用桩身应变可计算桩身轴力和边桩侧摩阻力。根据计算结果可知：边桩的轴力均为压力，且随施工进行，压力逐渐增大。边桩在0.50～1.75 m深度范围内，在扣拱开挖完成之前，出现了负摩阻力，经综合分析可能与后注浆施工有关。

2) 边桩同一深度处，迎土侧和背土侧的应变是不一样的，如图7～8所示。桩顶和桩端的差别明显，桩身中部的差别小，此规律符合圣维南原理。

3.4 边桩顶竖向位移

各监测点的边桩顶竖向累计变形量统计如表7所示。

表7 各监测点边桩顶竖向变形统计表 单位：mm

根据监测数据，边桩桩顶沉降的平均值为-5.80 mm。边桩顶的竖向位移与边桩承担的竖向荷载、边桩施工质量(桩侧泥皮、桩底沉渣、钻孔塌孔等)、桩身弹性压缩、桩端地层压缩变形、边桩的侧向水平位移等有关。

3.5 边桩桩身水平位移

各传感器的桩体水平变形统计如表8所示。桩体水平变形时程曲线如图9所示。

表8 不同边桩深度各施工阶段桩体水平变形值

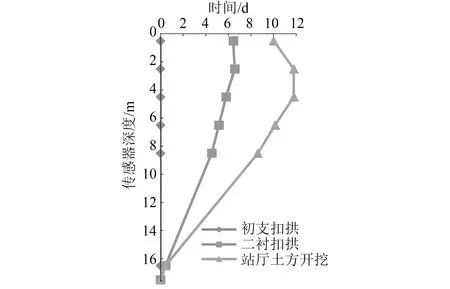
图9 边桩桩体水平变形图

从图9和表8可以看出：

1) 桩体水平位移均向车站内变形，主要发生在站厅层土方开挖期间和二衬扣拱施工期间。边桩主要受侧向水土压力作用产生侧向变形，初支扣拱前其边桩所受的边拱推力将与边导洞的侧向土压力平衡；二衬扣拱完成后进行主体土方开挖，边桩承受未开挖土体侧的水土压力，桩身发生侧向水平位移，但是桩顶部因已施工二衬结构可视作一道抵抗侧向变形的水平支撑，因此桩顶侧向位移受到控制。

2) 二衬扣拱完成后，桩体水平位移最大为6.58 mm，发生在深度为0.5 m和2.5 m处；站厅层土方开挖完成后，最大水平位移增加至11.81 mm，发生在深度为2.5 m和4.5 m的测点上，出现了鼓肚形现象。

4 结论

1) 总结出边桩在洞桩法暗挖车站施工过程中的三个受力阶段：第1阶段为初支扣拱期间。初支扣拱包括边跨扣拱和中跨扣拱，边跨扣拱初支结构一端直撑在边桩冠梁上并通过边桩承载受力；初支扣拱完成后，建立车站第二种稳定的结构体系，即土压力作用在初支拱上，通过纵梁和边桩冠梁向中桩及边桩传力。第2阶段为二衬扣拱期间。二衬扣拱需拆除中隔壁，应力重新分布。二衬扣拱完成后，土压力作用在初支上与二衬拱共同受力，通过纵梁和边桩冠梁向中桩及边桩传力。第3阶段为土方开挖阶段。随着车站土方的开挖，边桩作为围护结构，抵抗主体土方开挖产生的侧向土压力。

2) 边桩在主体土方开挖后桩侧摩阻力减少，轴力急剧向下传递，致使底板以下桩侧摩阻力和桩端力由桩基承担。因此在底板以下桩侧及桩端进行后压浆辅助措施有利于提高桩基承载力。

3) 根据边桩结构受力分析，主体土体开挖期间边桩受力状态发生显著变化，受力处于最不利的状态，建议设计时根据计算结果对边桩强度进行验算。

4) 边桩变形包括竖向变形和侧向水平变形。竖向变形包括荷载造成的桩身竖向变形及桩身自身压缩变形，施工中应重点控制边桩与中柱的差异沉降。边桩侧向变形主要发生在主体土方开挖后，边桩承受未开挖土体侧的水土压力，桩身发生侧向水平位移，但是桩顶部因已施工的二衬结构可视作一道抵抗侧向变形的水平支撑，因此桩顶侧向位移受到控制。

5) 根据本文监测数据分析，桩顶压力偏小，与理论计算荷载相差较大。建议用边桩混凝土应变数据进行反推边桩轴力计侧摩阻力，与理论计算荷载符合性较好。

6) 边桩的结构受力及变形特征符合摩擦桩的特点。不同之处在于主体土方开挖后，底板以上桩侧摩阻力减少，桩身发生侧向水平位移。设计时，建议仅取底板以下土体提供的桩侧阻力和桩端力，按照摩擦-端承桩进行设计。