城市轨道交通进出站短时客流预测模型研究

蔡昌俊

(广州地铁集团有限公司，510335，广州/正高级工程师)

0 引言

在城市轨道交通网络化运营时期，客流过饱和情况时有发生，这对车站运营组织工作提出了很高的要求。准确预测车站短时客流量，并据此制定科学的客运计划和组织方案，将有助于实现车站客流的动态管理，提高车站的运营效率。

目前，针对短期交通量预测的模型主要包括：数理统计模型，如时间序列模型[1]、卡尔曼滤波模型[2]等；人工智能模型，如支持向量机(SVM)[3]、长短时记忆网络(LSTM)、径向基函数(RBF)神经网络等；混合模型，如小波变换(WT)与自回归滑动平均模型(ARMA)的组合模型[8]、完全总体经验模态分解与LSTM的组合模型[9]、灰狼优化算法(GWO)与小波神经网络(WNN)的组合模型[10]、卷积神经网络(CNN)与LSTM的组合模型、WT与SVM的组合模型[14]等。以上研究成果对城市轨道交通客流预测具有重要的意义。但短时客流存在随机性、突变性、动态性等难以被精确预测的特点，对于短时客流预测，现有模型存在预测精度不够高或泛化能力不强等问题。数理统计模型对数据的随机变化不够敏感，针对随机性较强的短时客流，其预测性能比较有限[11]；人工智能模型能够描述城市轨道交通短时客流量数据的非线性特征，但对于海量的小粒度短时客流数据，其预测精度还有待进一步提高。混合模型综合了各种单一预测模型的优势，在一定程度上能够提高预测精度。但是，组合模型的组合方式及组合内容对预测精度的影响较大，因此需根据数据特点选择合适的组合模型。

循环神经网络(RNN)是一种强大的深度学习方法，可以将数据传递到先前的或同一层的神经元。LSTM是一种特殊的RNN，在各种各样现实问题上的表现都非常好[16]。Adam算法结合了Momentum和RMSProp两种算法的优点，可通过计算梯度的一阶矩估计和二阶矩估计，为不同参数设置自适应学习率，其学习率的取值接近Momentum算法，其收敛速率显著高于固定学习率的算法[17]。小波变换是一种数据预处理方法，在时域和频域都有着良好的局部分辨能力，在处理非线性和非稳定性数据方面具有很大的应用价值[18]，可以弥补传统LSTM模型没有考虑数据波动性的缺陷。因此，本文提出了一种基于小波变换和LSTM(即WT-LSTM)的组合模型，并利用Adam算法作为LSTM的训练算法，使用非饱和激活函数ReLU函数替代饱和函数激活函数Tanh函数。

1 组合预测模型构建

1.1 小波变换

城市轨道交通进出站客流量是随时间变化的信息，原始数据几乎都会受复杂因素的影响而携带一定的噪声，因此，需要采取一些方法提取、消除噪声。小波变换是目前应用最广泛的去噪方法，可克服傅里叶变换无法有效分辨时域信息的缺陷。小波变换分为连续型变换和离散型变换。本文采用离散型变换，其表达式为：

(1)

式中：

Ψj,k——离散型小波变换；

t——时刻；

a0——尺度参数；

b0——平移参数；

y(t)为基本信号函数；

Ψ(t)——母小波；

Ψ*——复共轭函数；

m——缩放常数；

n——平移常数。

常用的小波基函数包括Symlets、Daubechies、Haar等。

1.2 LSTM

LSTM可使用新的单元格解决通用RNN的长期依赖问题，从而确定信息的实用性。如图1所示，一个逻辑单元包含忘记门(Forget Gate)、输入门(Input Gate)和输出门(Output Gate)。

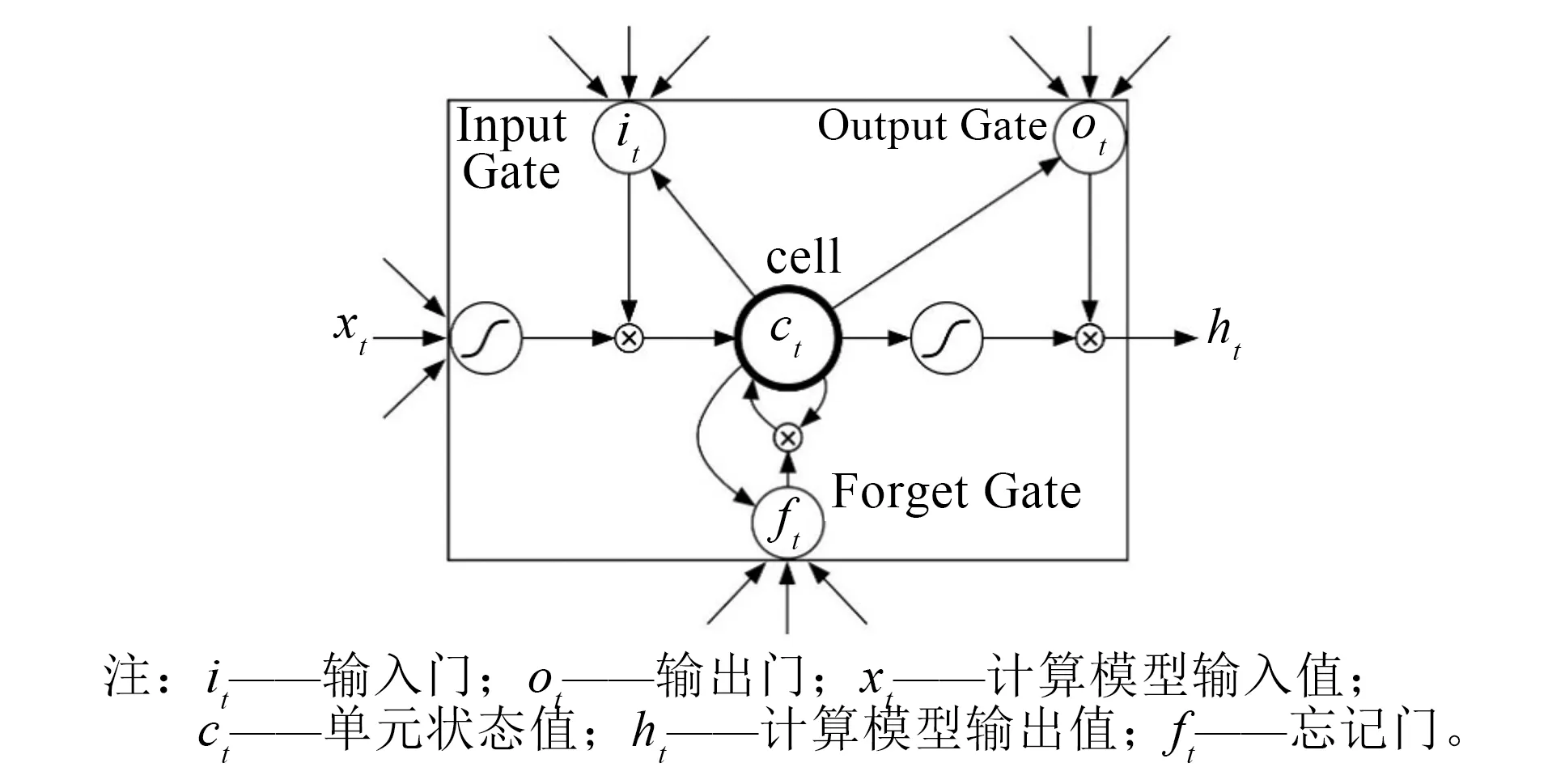
图1 LSTM结构图[19]

非饱和激活函数ReLU函数相对饱和激活函数(如Sigmoid和Tanh函数)，能解决“梯度消失”的问题，收敛速度更快。因此，本文利用ReLU函数来替代Tanh函数。 LSTM的工作过程如下：

步骤1：忘记门ft控制和选择逻辑单元所需要的信息，其由输入值xt和t-1时刻的隐藏层输出ht-1决定。表达式如下：

ft=σ(Wf[ht-1,xt]+bf)

(2)

式中：

σ——Sigmoid激活函数；

Wf——权重矩阵；

bf——偏置项。

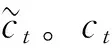
it=σ(Wi[ht-1,xt]+bi)

(3)

(4)

(5)

式中：

Wi——权重矩阵；

bi，bc——偏置项；

Wc——权重矩阵。

步骤3：隐藏层单元输出值ht由输出门ot和单元状态值ct计算获得，表达式为：

ot=σ(Wo[ht-1,xt]+bo)

(6)

ht=ot*ReLU(ct)

(7)

式中：

Wo——权重矩阵；

bo——偏置项。

步骤4：根据ht，进而可构造计算模型的均方误差。通过Adam算法最小化目标函数、Adam算法优化LSTM模型的过程见文献[20]。

1.3 WT-LSTM模型

WT-LSTM组合模型预测流程如图2所示。

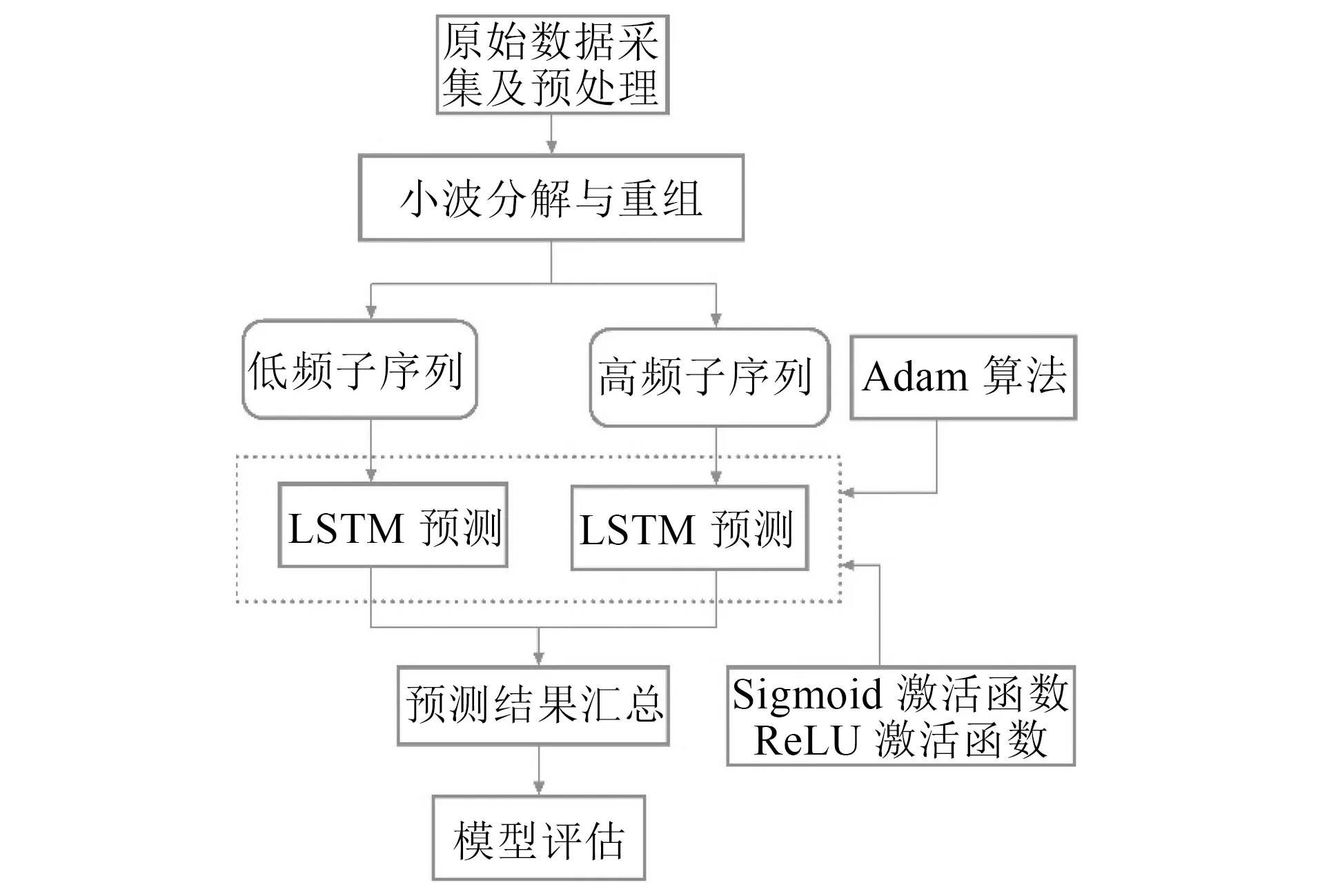
图2 WT-LSTM组合模型预测流程图

WT-LSTM组合模型实现步骤如下：

步骤1：从车站的AFC(自动售检票)设备终端获取历史客流数据，预处理后作为WT-LSTM模型的输入参数。本文数据预处理主要包括归一化处理，使原始值归一化为区间[0,1]中的值[21]：

(8)

xmid=(xmin+xmax)/2

(9)

式中：

xi——原始数据；

xmin，xmax——分别为原始数据的最小值和最大值。

步骤2：确定小波函数Ψ(t)和分解层数N。对原始信号采用Mallat算法作N层分解，得高频子序列D1,D2,…,DN和低频子序列AN；再利用Mallat算法重构公式，得重构高频子序列d1,d2,…,dN和低频子序列aN。重构后的序列与原始序列长度相同。小波分解和重构公式如式(10)和式(11)所示。

Di=GAi-1;Ai=HAi-1，i=1,…,N

(10)

式中：

H，G——分别为低通滤波器和高通滤波器；

i——分解层数；

A0——原始客流数据(当i=1时)。

ai-1=H*Ai+G*Di,i=N,N-1,…,1

(11)

式中：

H*，G*——分别为低通滤波器和高通滤波器的对偶算子。

步骤3：将高频子序列d1,d2,…,dN和低频子序列aN，分别代入到LSTM模型中进行分析及预测。通过变量控制方法确定LSTM模型的隐藏单元数量和迭代次数，并将Adam算法用于LSTM的短时客流预测中。

步骤4：汇总各子序列的预测结果，得最终预测结果。

步骤5：以广州塔站进出客流为例，评估基于Adam优化的WT-LSTM模型的优越性。选取平均绝对误差(EMAE)、均方根误差(ERMSE)、平均绝对百分比误差(EMAPE)以及决定系数(R2)4个常用指标作为本文模型的评估指标。

(12)

(13)

(14)

(15)

式中：

yi——实际值；

ypi——预测值；

yom——实际值的平均值。

2 案例分析

2.1 数据分析

广州塔站为广州地铁3号线和广州地铁APM(旅客自动运输系统)线的换乘站。本文选取广州塔站3号线2021年2月26日至2021年5月8日的进出站客流作为WT-LSTM组合模型的数据来源(剔除了清明节、五一的节假日数据与4月19日的异常数据)。为保证数据的完整性，指定每日记录时段为06:00—23:00。本文选取5min的时间间隔作为短时客流的统计时长，15 min的时间间隔作为短时客流的预测时长。此外，本文客流预测的分析长度为30 d，即采用时刻t的前30 d历史客流数据来实现时刻t的客流预测。以低频子序列aN为例，自第一个样本数据块[(a1.i,a2.i,…,a30.i),a31.i]起，依次下滑数据最后得[(aT-30.i,aT-29.i,…,aT-1.i),aT.i]，这样滑动共获得T-30个数据块。对于aN的全部数据，本文以5.0∶2.5∶2.5的比例分成训练集、验证集和测试集。

为直观地分析广州塔站的客流特征，随机选取一周的进出站客流，如图3所示。由图3可见，广州塔站工作日进出站客流曲线的整体分布相似，具有周期性特征。其中，工作日出站客流高峰集中在07:30—10:00之间，进站客流高峰则集中在17:00—21:00之间；周末的进出站高峰都集中在晚高峰，出站客流高峰在17:00—21:30之间，周六的进站客流高峰在19:00—22:30之间，周日的进站客流高峰在19:00—22:00之间。这说明广州塔站是典型的商业区。工作日进站客流高峰的进站人数为619人/5 min，出站客流高峰的出战人数为571人/5 min；周末进站客流高峰的进站人数为580人/5 min，出站客流高峰的出站人数为512人/5 min。由图3可知，06:00—07:00及23:30—24:00的客流量较少，因此，本文预测数据不包括这两个时间段的客流量。

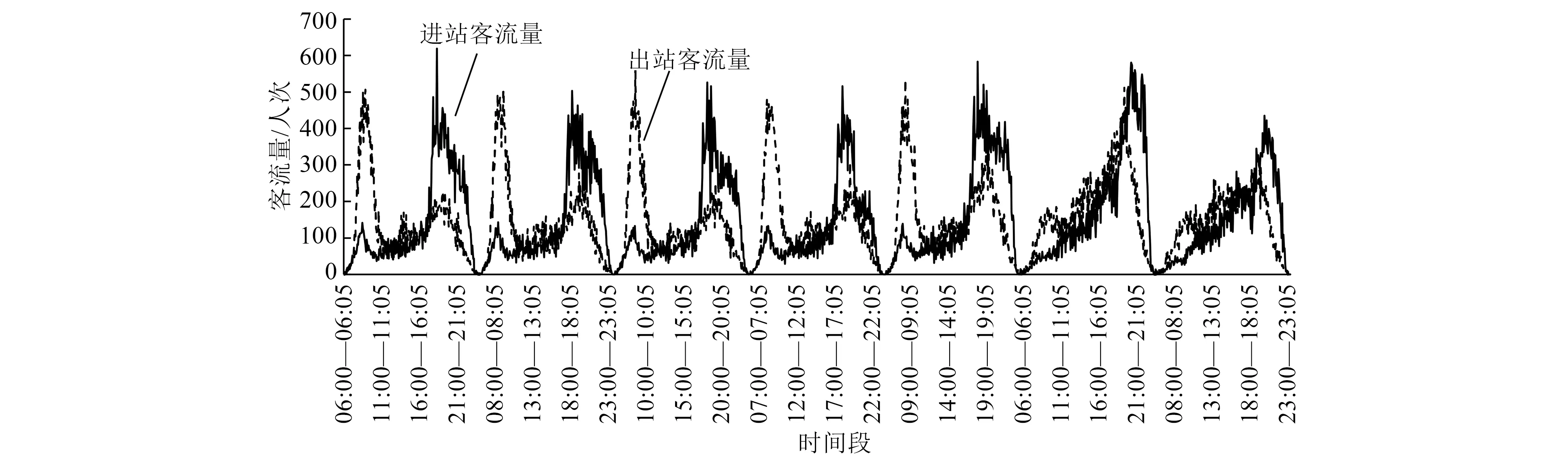
图3 广州塔站样本数据中其中一周的进出站客流量

2.2 WT-LSTM模型参数调优

2.2.1 小波函数的选择

文献[22]指出，Daubechies(dbN)和Symlets(symN)小波函数对城市轨道交通客流数据的去噪效果都很好。因此，本文分别利用dbN和symN小波函数对车站客流数据进行分解，并对出站客流的预测结果进行比对。小波分解深度为2层，LSTM的优化采用Adam算法，LSTM最大迭代次数为90，LSTM隐含层节点数为25，试验结果如表1所示。

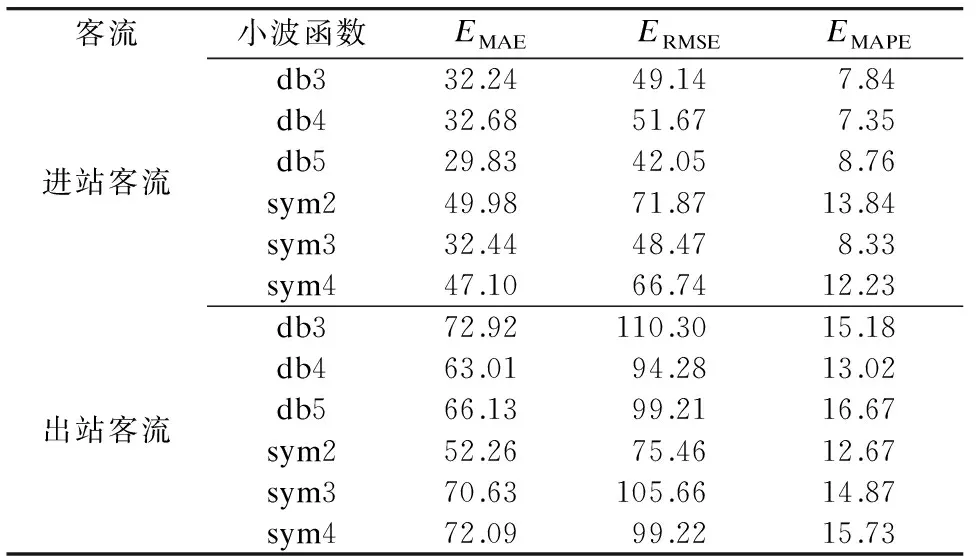
表1 不同小波函数性能对比

由表1可知：当WT-LSTM组合模型的小波函数为db4时，进出站客流数据的预测精度最高。进站客流数据的EMAE、ERMSE和EMAPE分别为32.68、51.67和7.35；出站客流数据的EMAE、ERMSE和EMAPE分别为63.01、94.28和13.02。

2.2.2 小波分解深度选择

小波分解层数选取数值越大，细节分量的低频信息体现得越明显，但其自身的高频信息也会被渐渐分离开；同时，高频子序列也含有一定的低频信息，这会增加客流量分析的复杂程度。因此，本文分别选择两层和三层分解深度对车站的客流数据进行分解。小波函数为db4，LSTM的优化采用Adam算法，LSTM最大迭代次数为90，LSTM隐含层节点数为25，试验结果如表2所示。

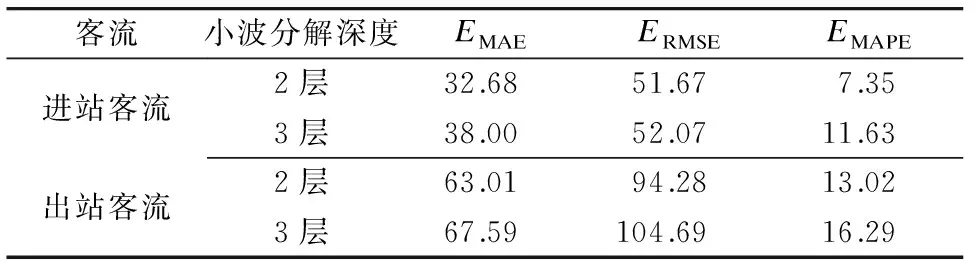
表2 不同小波分解深度性能对比

由表2可知，WT-LSTM组合模型的小波分解深度为2时，进出站客流数据的预测精度更高。

2.2.3 LSTM优化算法选择

分别利用RMSProp、SGD和Adam算法对LSTM进行寻优。小波函数为db4，小波分解层数为2层， LSTM的迭代次数90，隐含层节点数为25，试验结果如表3所示。由表3可知，Adam算法优于RMSProp和SGD算法。

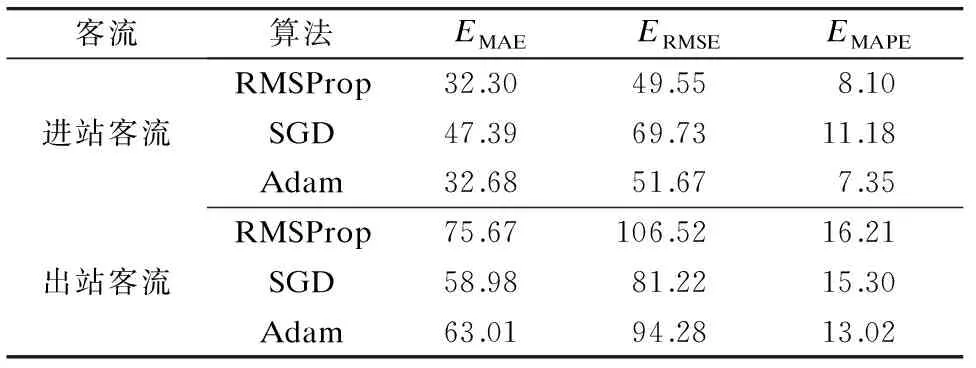
表3 不同算法性能对比

2.2.4 LSTM节点数和迭代次数选择

LSTM隐含层节点数和迭代次数对模型预测精度的影响很大，因此，本文首先选取隐含层节点数为20、25、30，迭代次数90，对出站客流进行预测比对。选取迭代次数为80、85、90、95、100，隐含层节点数25，进行比对(出站客流数据的迭代次数为95时，同时选取30的节点数。)，以获取合适的迭代次数。小波分解层数为2层，小波函数位db4，LSTM的优化采用Adam算法。试验结果如表4和表5所示。

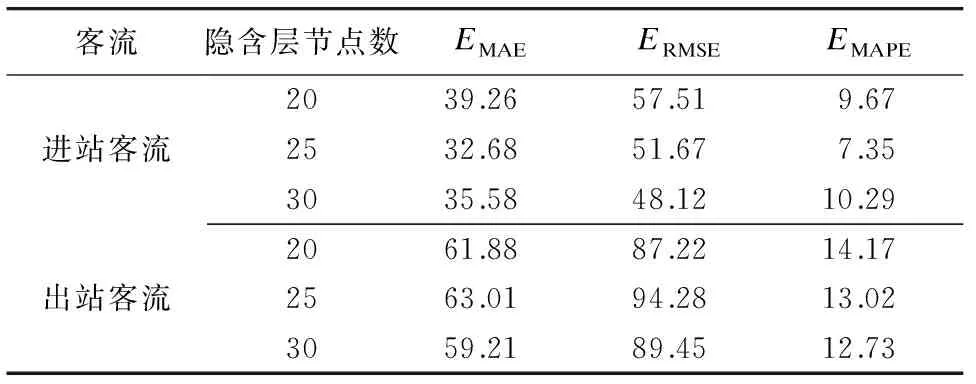
表4 不同隐含层节点数性能对比

由表4可知：LSTM隐含层节点数取25时，进站客流数据预测精度更高；LSTM隐含层节点数取30时，出站客流数据预测精度更高。由表5可知：LSTM迭代次数为95时，进出站客流数据的预测精度更高；迭代次数为95时，隐含层节点数为25时，出站客流数据的预测精度更高。

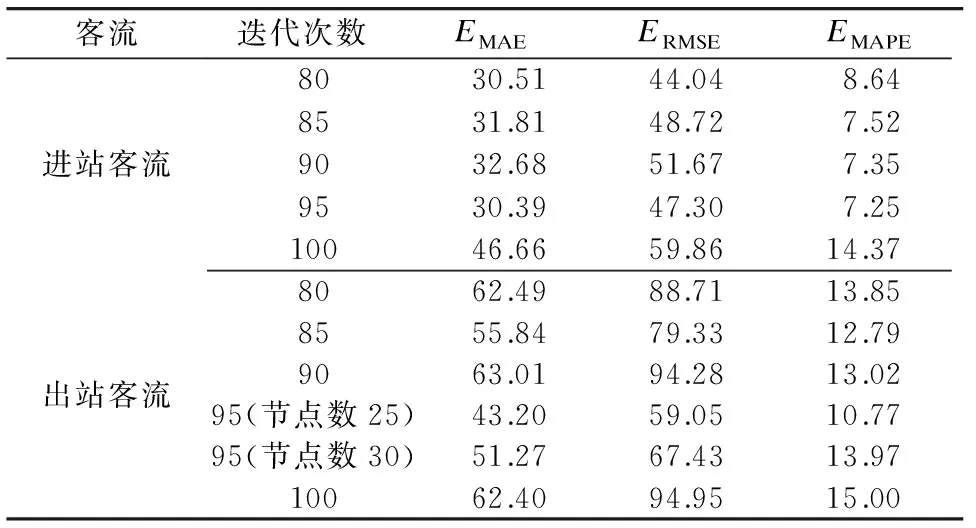
表5 不同迭代次数性能对比

综合表1～5参数调优可知：本文 WT-LSTM组合模型的小波函数为db4、小波分解层数为2层、LSTM优化算法为Adam、LSTM最大迭代次数为95、LSTM隐含层节点数为25时，模型的预测效果最佳。此时，进站客流数据的EMAE、ERMSE和EMAPE分别为30.39、47.30和7.25；出站客流数据的EMAE、ERMSE和EMAPE分别为43.20、59.05和10.77。

2.3 LSTM和WT-LSTM组合模型的比较

本文WT-LSTM组合模型选取小波函数为db4，小波分解层数为2层，LSTM的优化采用Adam算法，LSTM最大迭代次数为95，LSTM隐含层节点数为25，并与传统LSTM模型进行比较。经模型计算，LSTM模型预测结果如图4所示，WT-LSTM组合模型的预测结果如图5所示。预测性能对比如表6所示。

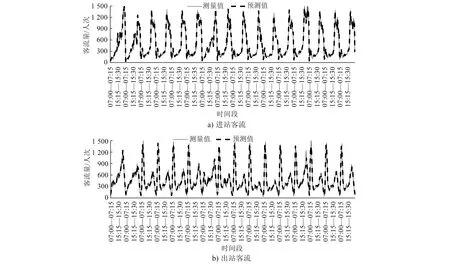
图4 LSTM模型的进出站客流预测结果

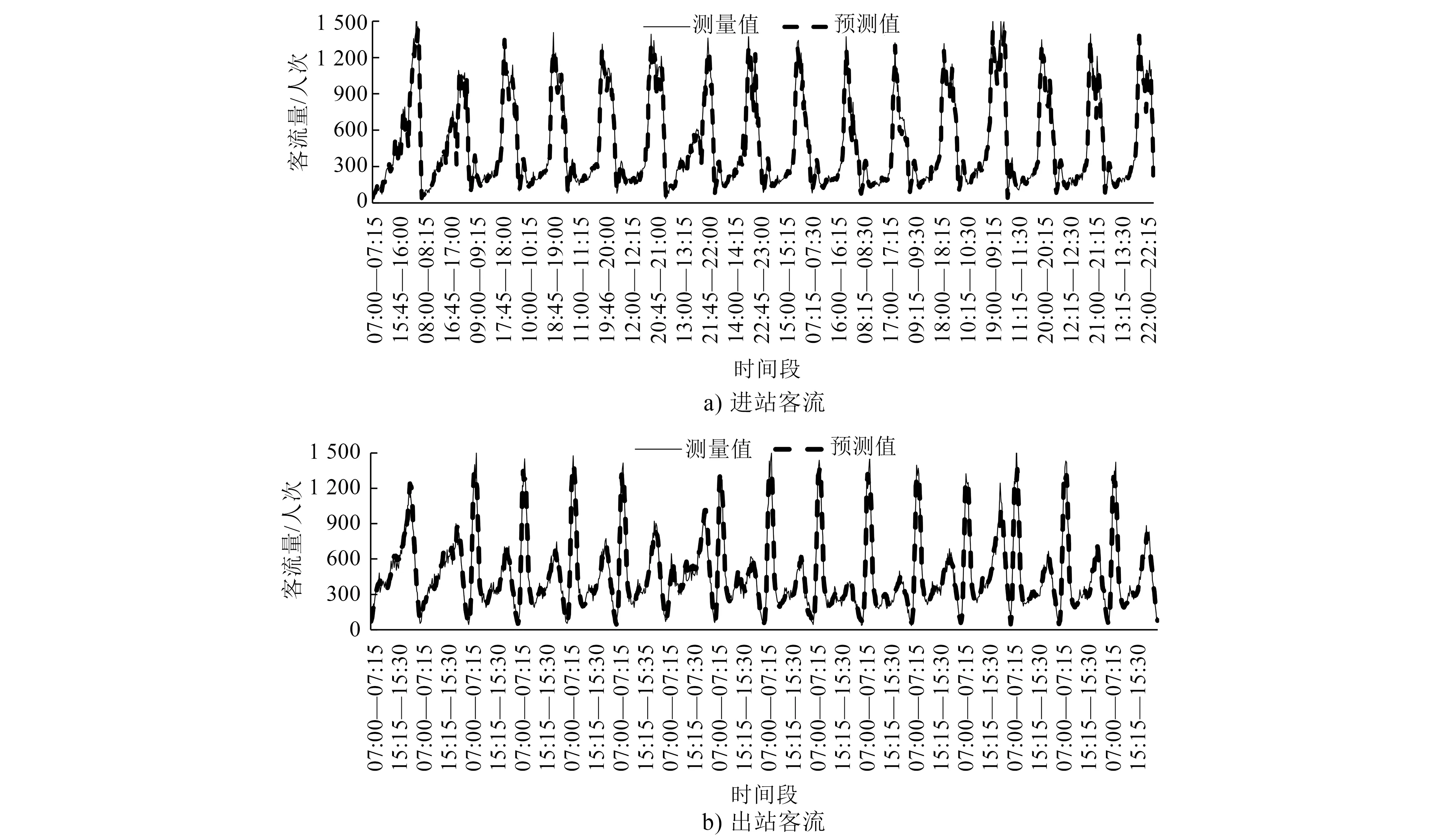
图5 WT-LSTM模型的进出站客流预测结果

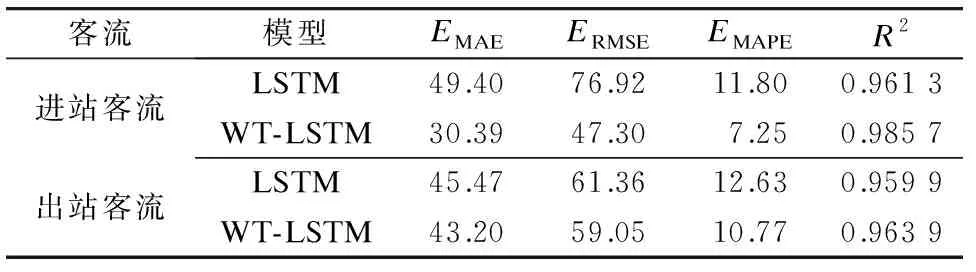
表6 LSTM和WT-LSTM模型的预测性能对比

由图4和图5对比可知，LSTM模型的预测结果能够在一定程度上预测实际数据的变化，但预测误差较大；WT-LSTM组合模型的预测结果与实际数据非常接近。由表6可知：WT-LSTM组合模型相比LSTM模型，在EMAE和EMAPE方面都有较大提升，ERMSE和R2也佐证了WT-LSTM模型的预测优势。

3 结语

针对城市轨道交通短时客流的特征，结合小波变换理论和LSTM模型设计了WT-LSTM组合预测模型，并利用Adam算法对LSTM进行优化，使用非饱和激活函数ReLU函数替代饱和函数激活函数Tanh函数。经参数调优后可得：WT-LSTM组合模型的小波函数为db4、小波分解层数为2层、LSTM优化算法为Adam、LSTM最大迭代次数为95、LSTM隐含层节点数为25时，组合模型的预测效果最佳。

为了验证所建WT-LSTM组合模型的预测效果，将组合模型与传统的LSTM模型进行比对。研究结果表明，WT-LSTM组合模型在EMAE、ERMSE、EMAPE和R2方面均优于LSTM模型。WT-LSTM组合模型的优势是，仅考虑数据本身，不用考虑站外天气、其他车站客流情况、站外大型活动等影响因素。此外，该模型对于具有时间序列特征的客流数据都具有较高的预测精度。