Heaviside函数的Laplace变换建立超静定梁挠曲线方程

王海林，王吉民

（浙江科技学院 建筑工程学院，杭州310023）

梁作为实际工程中应用广泛的构件，它在外荷载作用下引起的弯曲变化受到高度的重视，而作为与之相紧密联系的挠曲线方程的计算问题，也就成了材料力学中的一个重要内容。关于梁挠曲线的计算方法有很多，如积分法、能量法、图乘法、共轭梁法、变分法等。目前，在大部分的材料力学教材中，梁挠曲线方程的首选计算方法是积分法，但是在实际的工程分析中，由于梁上常常作用有多种荷载，用积分法需要在梁的连续性条件和边界条件的基础上确定各段相应的积分常数，致使过程显得非常繁琐，因此不是很实用。

文献［1］提供了一种在Laplace变换的基础上求解梁挠曲线方程的方法。本研究以此方法为基础，将Heaviside函数直接引入梁的弯矩方程，从而构造出全梁通用方程，并对该方程进行Laplace变换，通过梁的基本方程并结合边界条件，直接计算出超静定梁的挠曲线方程，从而进一步简化了计算过程，减少了计算量，为超静定梁挠曲线方程的求解提供了一种较为快捷的计算模式。

1 Heaviside函数及相关性质

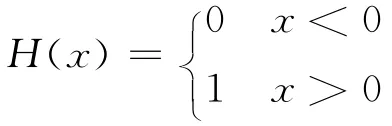
上式即为Heaviside函数，常记为H（x），由于其在x＝0处发生跳跃，故又称为单位阶跃函数（unit step function）。Heaviside函数具有多种性质，它还是δ（x）函数的原函数［2］。关于Heaviside函数，可参考相关文献，这里不赘述。

2 梁通用方程的建立

2.1 基本公式

材料力学［3］中，考虑小变形状态，梁的挠曲线近似微分方程为

2.2 利用Heaviside函数建立通用方程

有一悬臂梁，分别在该梁上作用集中力P（图1），力偶M（图2），均布荷载q（图3）

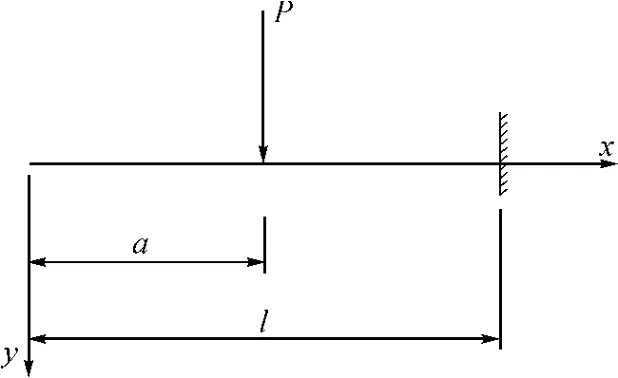
图1 集中力P作用下的悬臂梁Fig.1 Cantilever beam under concentrated force P

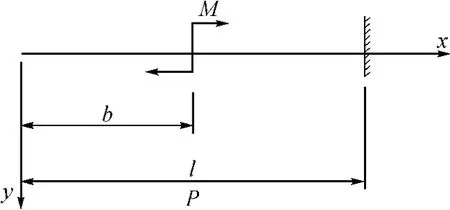
图2 力偶M作用下的悬臂梁Fig.2 Cantilever beam under force couple M

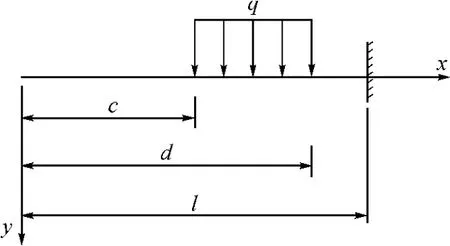
图3 均布荷载q作用下的悬臂梁Fig.3 Cantilever beam under uniform load q

2.2.1 集中力P作用下悬臂梁弯矩值M（x）的表达

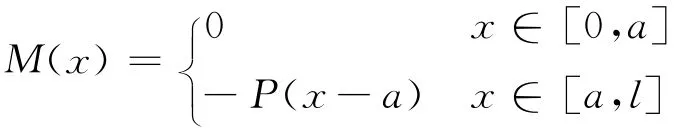
引入Heaviside函数，所以，有

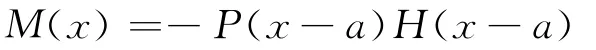
2.2.2 力偶M作用下悬臂梁弯矩值M（x）的表达

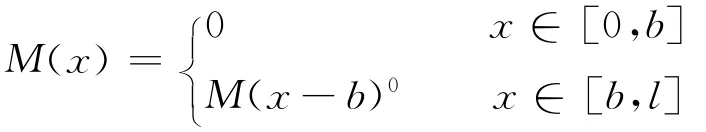
所以，有

2.2.3 均布荷载q作用下悬臂梁弯矩值M（x）的表达

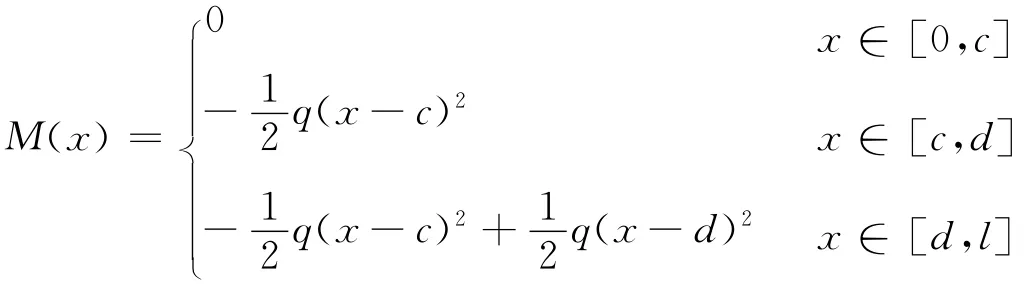
所以，有

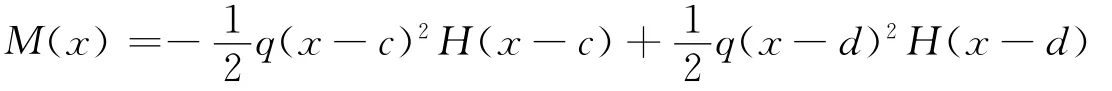
2.3 一般情况

所以，基于小变形和线弹性情况下的叠加原理，对于该悬臂梁，不管梁上作用有上述荷载中的几种，弯矩M（x）均可表示为一个如下的通用方程：

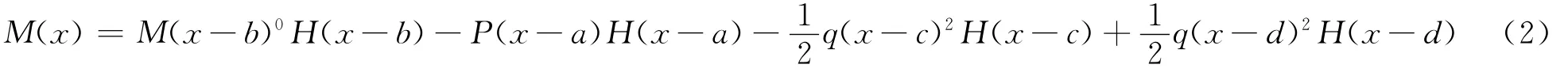
将该通用方程（2）带入挠曲线近似微分方程（1）式，有

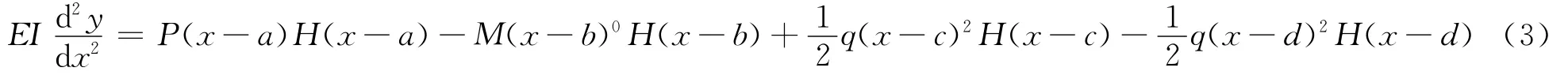
3 挠曲线方程的Laplace变换

3.1 Laplace变换具有的主要性质有

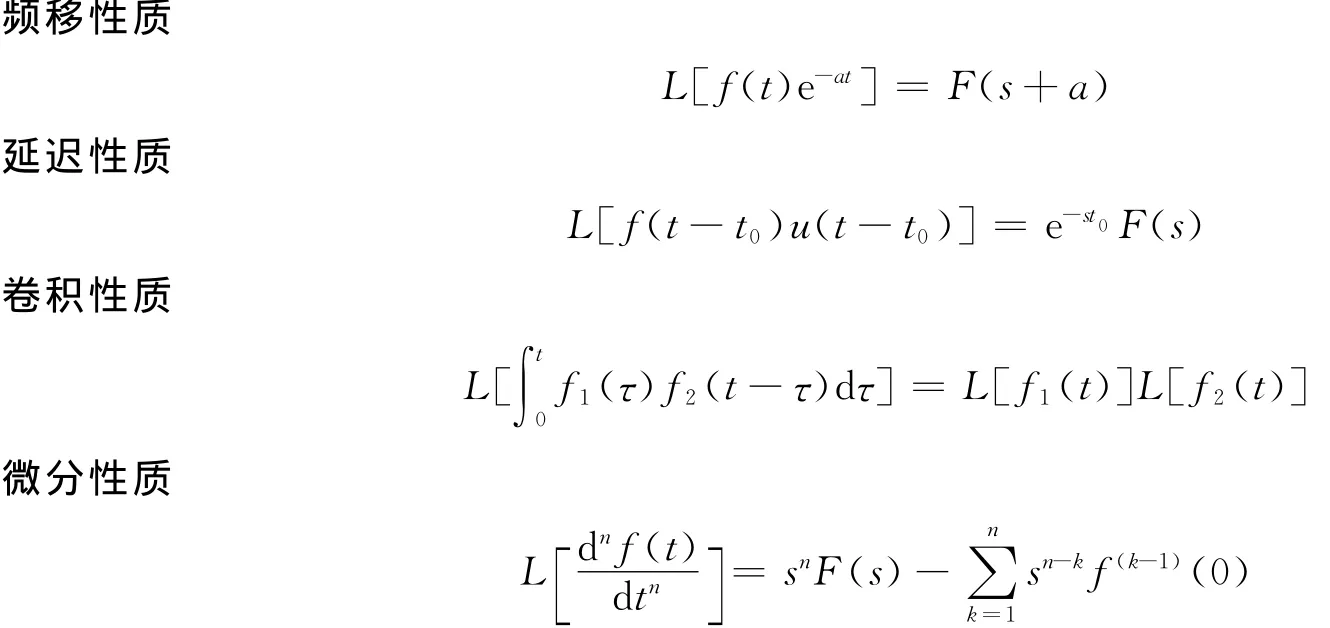
3.2 对式（3）进行Laplace变换

结合上述所列的Laplace变换性质，式（3）左右进行变换，有

化简整理，得

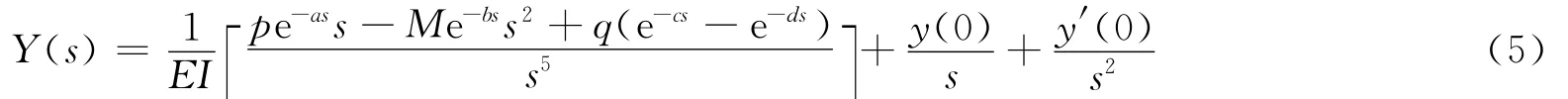
对（5）式进行反Laplace变换，有

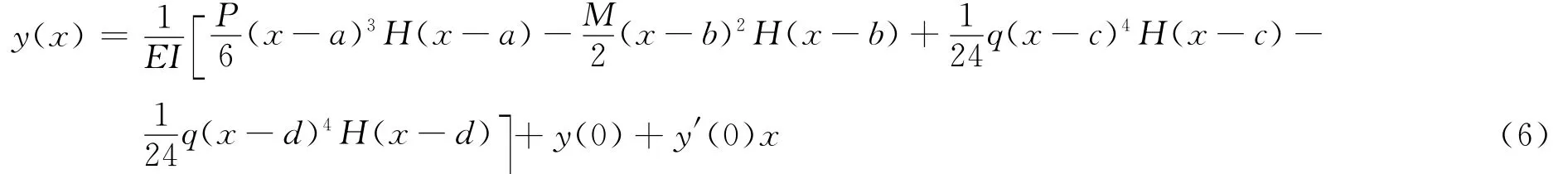
故，式（6）即为基于Heaviside函数的梁通用挠曲线方程。

4 算 例

4.1 方法验证

如图4所示，有一受均布荷载作用下的两端固定梁，首先定义：设梁A端反力为RA，B端反力为RB，方向均竖直向上；梁A端弯矩为MA，B端弯矩为MB，顺时针为正。

于是，根据式（6），有

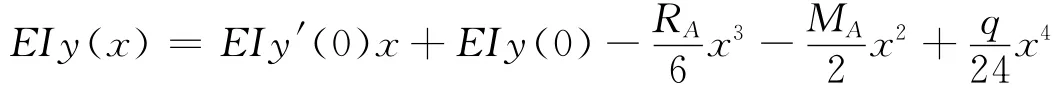
利用边界条件：y｜x＝0＝0，得y（0）＝0；y′｜x＝0＝0，得y′（0）＝0

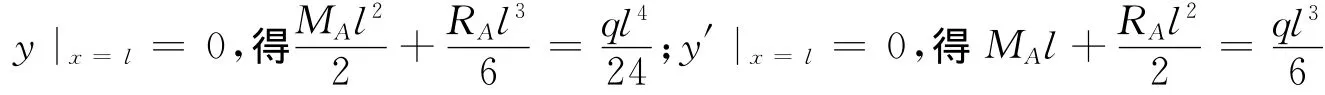
联立两式，求解得

同理，得出A，B的固端剪力，综合后即

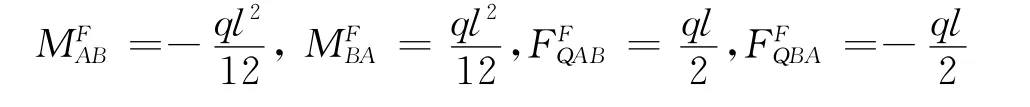
这个结果与结构力学［4］等截面杆件的载常数表中所列的情况完全一致，故该方法正确。所以，化简后，均布荷载作用下的两端固定梁挠曲线方程为

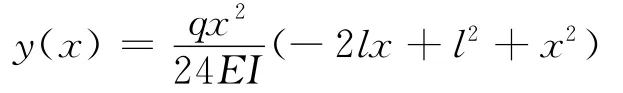
这个方程与结构静力计算手册［5］给出的方程相同。

4.2 实 例

如图5，有一超静定梁，各荷载均标于梁上，根据（6）式，有

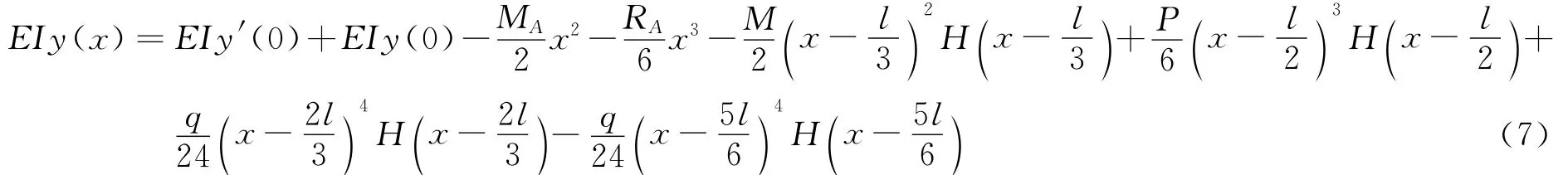
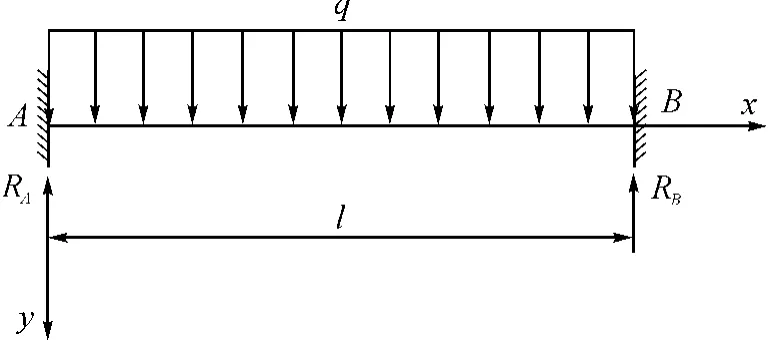
图4 均布荷载作用下的两端固定梁Fig.4 Both ends clamped beams under uniform load

图5 超静定梁简图Fig.5 Diagram of statically indeterminate beam

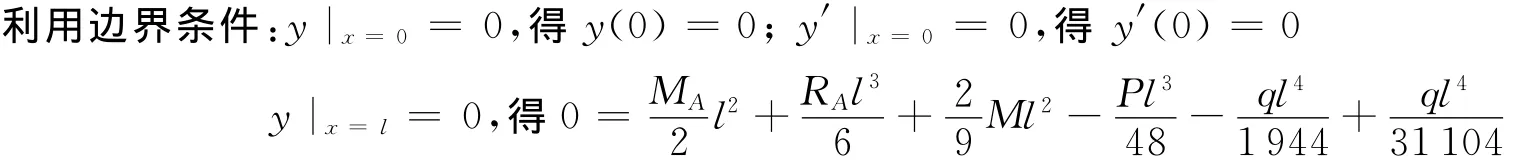
补充静力方程，对B取矩

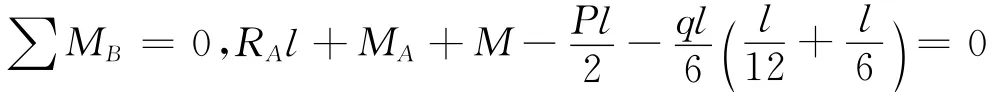
联立两式求解，并用MATLAB［6］符号计算验证结果，得

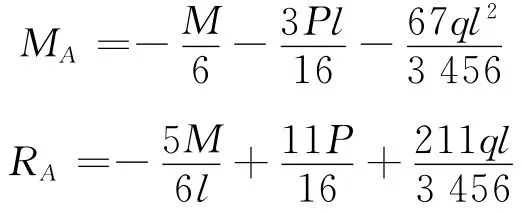
代入式（7），即可得出该超静定梁的挠曲线方程。

5 结 语

从上述的推导及实例的计算可以看出，本文所述的方法在求解超静定梁挠曲线方面，计算量少，比较快捷、方便，因此具有一定的实用性。

［1］ 刘明超，丁晓燕．拉氏变换求解梁的挠曲线方程［J］．力学与实践，2012，34（2）：78-80．

［2］ 梁昆淼．数学物理方法［M］．4版．北京：高等教育出版社，2010：83．

［3］ 王吉民．材料力学［M］．北京：中国电力出版社，2010：107-108．

［4］ 龙驭球，包世华．结构力学Ⅰ：基本教程［M］．2版．北京：高等教育出版社，2006：281-283．

［5］ 国振喜，张树义．实用建筑结构静力计算手册［M］．北京：机械工业出版社，2009：297．

［6］ 薛定宇，陈阳泉．高等应用数学问题的MATLAB求解［M］．北京：清华大学出版社，2008．