厌氧反应器停留时间分布测定及流动模型研究

张良佺，徐 晖

（浙江科技学院 生物与化学工程学院，杭州310023）

高效厌氧反应器运行必须具备两个基本前提条件［1-2］：一是强有力的微生物固体截留能力，厌氧反应器运行过程中活性污泥高度颗粒化，使得大量微生物菌群能够附着其上，提高了微生物分布密度，促进了复杂有机物的快速转化和产物甲烷的快速生成；二是良好的水力混合条件，厌氧反应器通过构造上的改进，其中废水流动大多呈平推流与完全混合流相结合的复合型流态，从而延长了废水在反应器内的流动途径，泥水两相能够实现良好的接触。

当前，对微生物反应机理及其相关模型研究［3-6］较多，但对反应器中废水的流动状态研究则十分稀少，尤其是反应过程中气体甲烷、二氧化碳的产生，将极大地影响着废液流动型态，进而影响到反应结果，相关研究迄今未见文献报道。笔者在研究污泥颗粒流化特性的基础上［7］为考察液相流动过程对微生物反应过程的影响，通过对实际反应器中液相停留时间的冷模测定，研究了不同气体流量下反应器流动状况的变化，并在此基础上建立了废水的流动组合模型，依据实验数据测定了模型参数，为下一步的反应器模拟与优化打下了基础。

1 冷模试验装置

1.1 蠕动泵的标定

实验所用蠕动泵，由于泵上显示的是其转数，因此实验之前必须对泵进行标定，以获得转数与流量之间的关系，结果见图1。

对实验数据进行回归，获得泵的流量与转数之间关系如下：

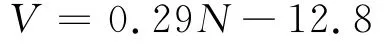
式中：V— 流量，L／h；N— 泵转数，r／min。

由数据相关性R值可知，流量与转数之间具有较好的线性关系。

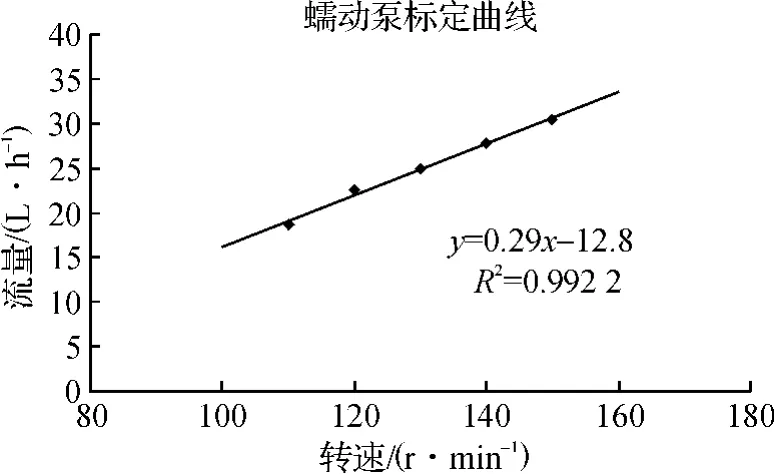
图1 蠕动泵标定曲线Fig.1 Calibration curve of peristaltic pump

1.2 工艺流程

以水为工作介质进行冷模实验，工艺流程示意见图2。由进水罐1加水至一定高度，开启蠕动泵2，保持一定流量，流量计安装在泵出口处；同时开启气泵3，气泵流量由安装在泵出口处的气体流量计检测。水从下而上流过反应器，反应器上部有一气液分离装置，气体导入集气箱5，液体则在分离器上部出口处排出，液体出口处安装一电导仪，通过检测出口液体的电导率而推导出浓度的高低。

当气液两相流动达到稳定后，在进水罐上方快速加入一定量的示踪剂，同时计时，间隔一定时间，于反应器出口处记录下水的电导率随时间的变化。

改变气体流量，重复以上过程。

实验过程所用仪器如表1所示。

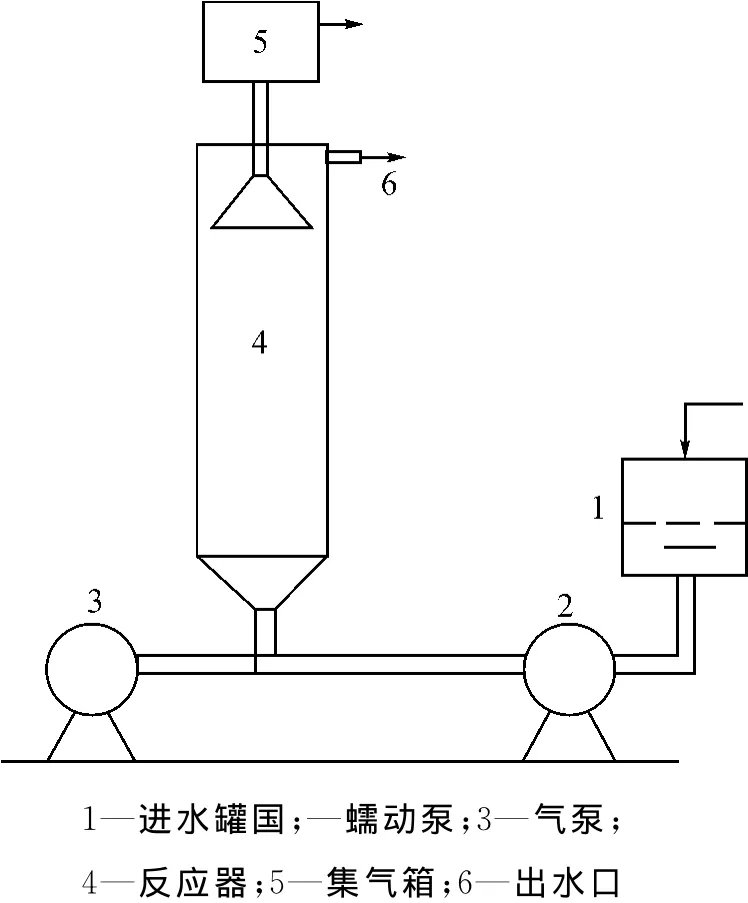
图2 工艺流程示意图Fig.2 Flow chart

表1 实验仪器Table 1 Experimental apparatus

2 流体流动模型建立

对反应器流动状况作出假设：示踪物为瞬间进料；反应器中气体流量恒定不变，且均匀上升；进料清水流量亦恒定不变。

通过对实验数据进行分析，观察E（t）-t曲线，假设厌氧反应器流动型态可由一平推流反应器与两个并联的全混釜反应器进行串联组成，模型示意图如图3所示。

说明：设反应器总体积为VR，VR等于模型中各反应器体积VRi之和，两个CSTR的体积分率分别为f1、f2，总流量为v0，流经CSTR1的流量分率为I，CSTR1、CSTR2反应器的出口浓度分别为CA1、CA2，出口总浓度为CA。

设PFR的体积分率为f3，则：f3＝1-f1-f2

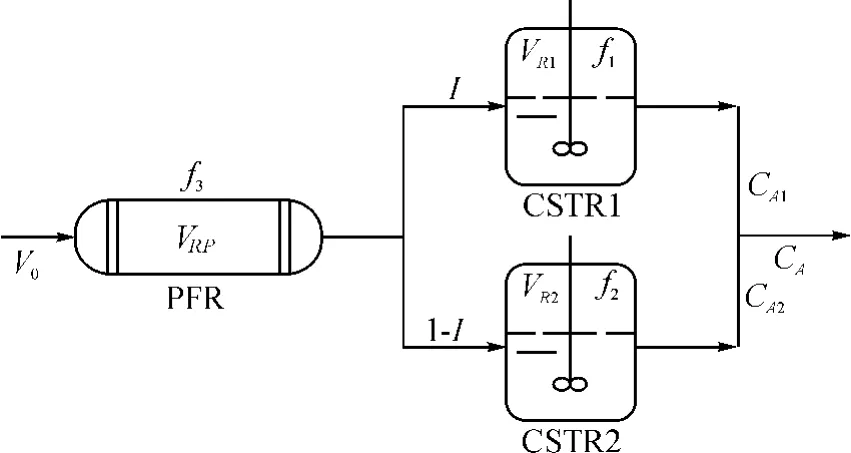
图3 反应器流动模型组合示意图Fig.3 Schematic diagram of reactor combination of flow model

当t＝0时，在PFR反应器入口处，用蠕动泵脉冲输入质量为M的饱和示踪剂溶液。

对PFR：

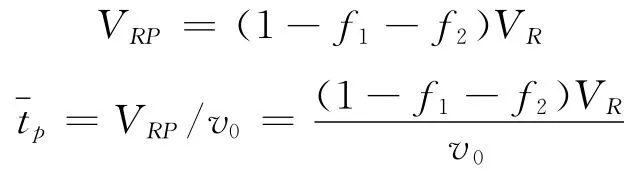
式中：VRP—PFR的体积；tp—PFR的平均停留时间。

对CSTR1进行物料衡算，求取CSTR1出口浓度CA1：

当t＜tp时，由于示踪剂仍在PFR中，对CSTR1，CA1＝0。

当t≥tp时，对CSTR1作物料衡算：

根据输入量＝输出量＋累计量

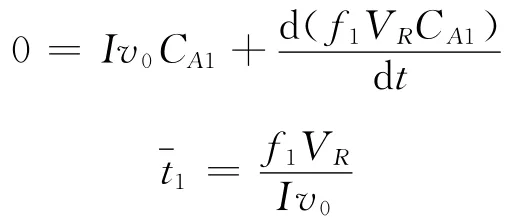
t1为CSTR1的平均停留时间。

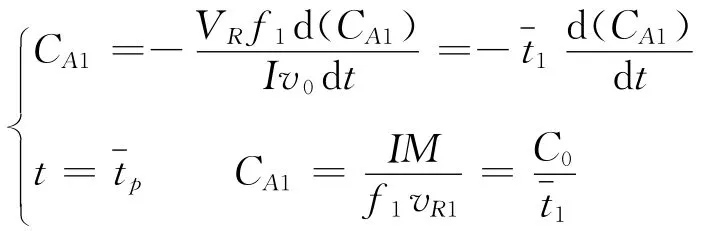
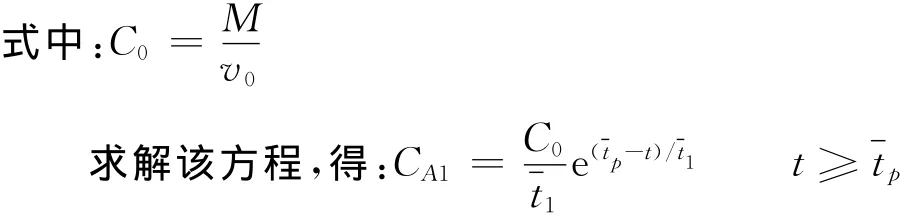
同理，对CSTR2进行物料衡算，可求取CSTR2出口浓度CA2：

当t＜tp时，由于CSTR2中无示踪剂，故：CA2＝0

当t≥tp时，对CSTR2作物料衡算，可得：

最后，对CSTR1和CSTR2出口处作物料衡算，由于该处进行的是混合过程，则：

当t＜tp时，CA＝0。

当t≥tp时，CA＝ICA1＋ （1-I）CA2

停留时间分布密度函数E（t）的求取：

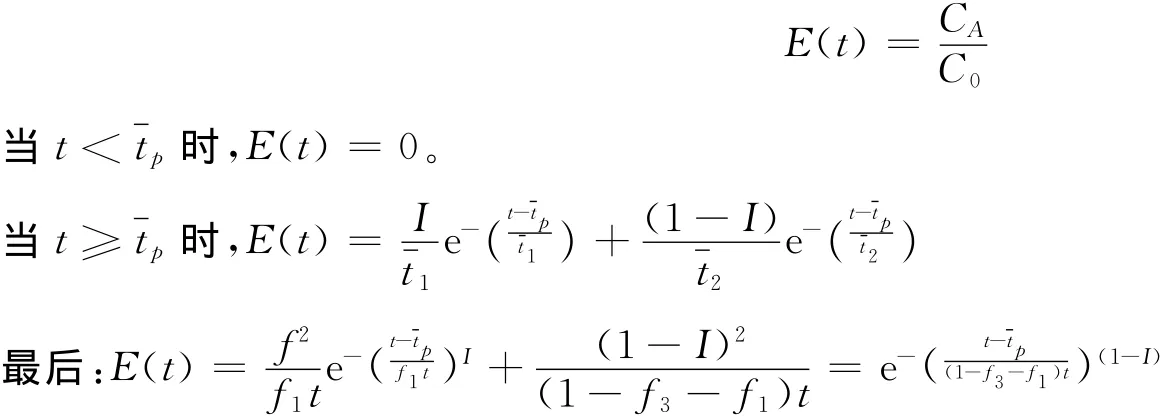
对模型求解转化为求解一个三参数I、f1、f3的E（t）方程，式中tp不是独立的。

3 实验结果及模型参数求解

3.1 实验数据

实验在常温下进行，在恒定的液体流量下，当气体流量不同时，分别测定出口电导率，测定部分结果见表2。

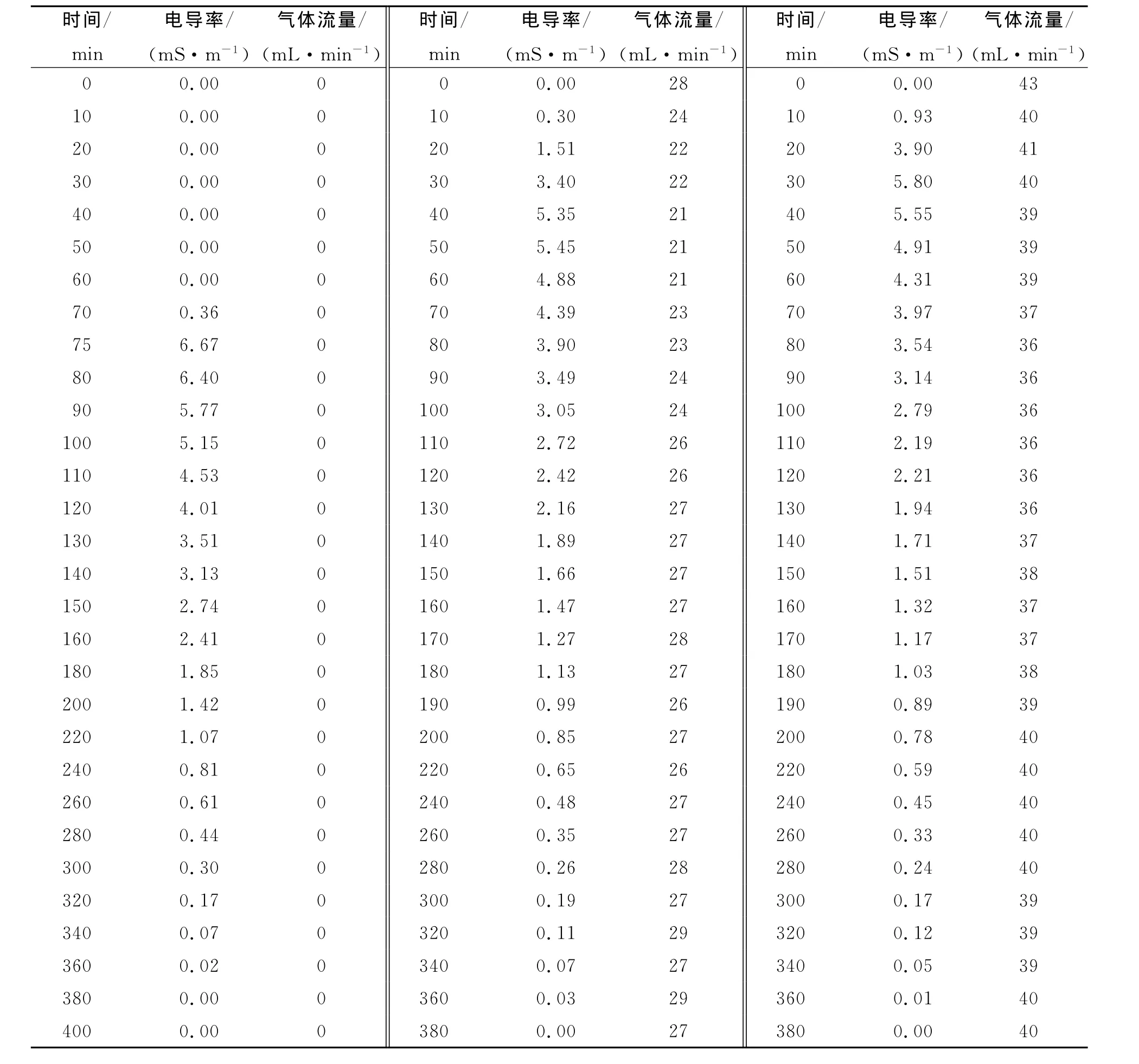
表2 实验数据Table 2 Experimental data

对三个气体流量求取平均值，分别为0、25、38mL／min。

3.2 非线性最小二乘法求解模型参数

模型采用最小二乘法拟合E（t）方程，进而求得模型参数I，f1，f2，目标函数设立为：

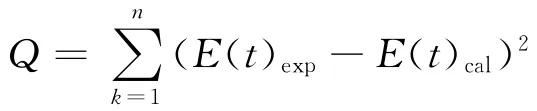
式中：Q— 残差；E（t）exp— 实验值；E（t）cal— 计算值。

利用excel规划求解功能，对非线性方程E（t）采用对分法进行求解，计算结果分述如下。

3.2.1 总的平均停留时间t及方差σ2的求解

表3 t与σ2随气体流量之间的变化关系Table 3 Change relationship oft andσ2 with gas flow

相对误差：

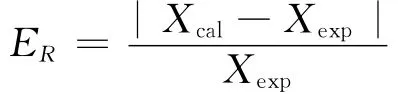
式中：Xcal— 计算值；Xexp— 实验值。

在不同的气体流量下，平均停留时间的相对误差在5%以内，无因次化方差的相对误差在10%左右，说明计算值与实验值有良好的符合度。

由表2可知：随气体流量的增大，无因次方差σ2越来越大，表示厌氧反应器流型越来越接近于全混流。

3.2.2 模型参数f3的求解

PFR的平均停留时间tp可以直接从实验数据中读取，体积分率则为：

根据实验数据，本研究选取tp值的方法为：E（t）开始不为0时和达到最大值时的中间值作为其平均停留时间。

当气体流量不同时，由实验数据可得tp，进而算得f3，数据见表4。

由表4可知：随着气体流量的增加，f3下降明显，说明气体通过的量对模型参数有显著的影响。其根本原因在于：随着气体流量的增加，反应器内返混程度增加，故体积分率f3迅速下降。

3.2.3 模型参数流量分率I及CSTR反应器体积分率f1、f2的求解

不同气体流量下I、f1、f2最佳值见表5。

由表5可知，当气体流量为0时，非线性方程出现多解，但气体流量的变化对流量分率参数I的影响比较小，基本保持在0.6～0.75之间；反应器CSTR1的体积分率f1随气体流量增加而增加，反应器CSTR2的体积分率f2随气体流量的变化出现极值，到达0.3后反而有所减小。

表4 不同气体流量下的tp及f3Table 4tp、f3values under different gas flow

表5 参数I、f1和f2Table 5 Parameters I，f1and f2

3.2.4 不同气体流量下E（t）模型计算值与实验值的比较

当气体流量为0mL／min时，将模型参数I＝0.7、f1＝0.35、f2＝0.15；I＝0.6、f1＝0.3、f2＝0.2的数据代入E（t）方程，得到E（t）-t曲线，并与实验值进行对比，如图4所示。

由图4可知：模型曲线与实验曲线有良好的符合度，其中I＝0.7时较I＝0.6似更优越，E（t）的最大相对误差为10.2%，说明该组合模型能反映实际情况。

结论：当气体流量为0时，最佳参数为I＝0.7、f1＝0.35、f2＝0.15。

当气体流量为25mL／min时，将模型参数I＝0.75，f1＝0.45，f2＝0.3的数据代入E（t）方程，得到相应曲线，并与实验曲线比较，如图5所示。

由图5可知：当气体流量为25mL／min时，模型曲线与实验曲线有很好的符合度，E（t）的最大相对误差为15.4%。

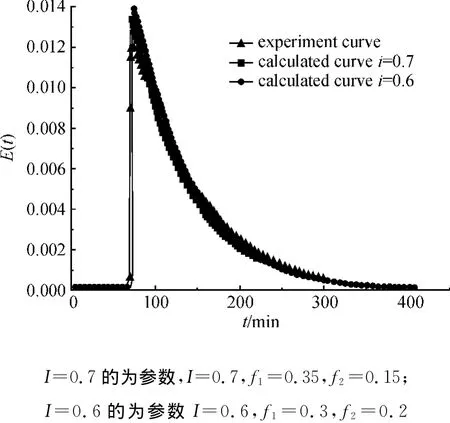
图4 气体流量为0mL／min时实验与模型曲线Fig.4 Comparison between experiment curve and model curves when gas flow is 0mL／min

当气体流量为38mL／min时，将参数I＝0.70，f1＝0.55，f2＝0.25的数据代入E（t）方程，得到E（t）-t图，并与实验数据对比，结果如图6所示。

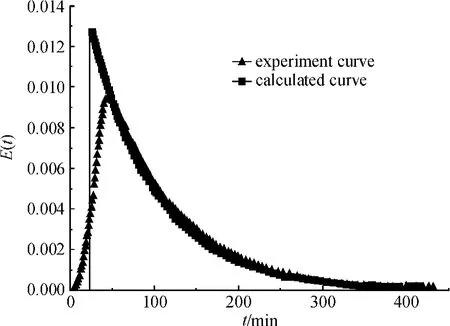
图5 气体流量为25mL／min时实验与模型曲线Fig.5 Comparison between experiment curve and model curve when gas flow is 25mL／min

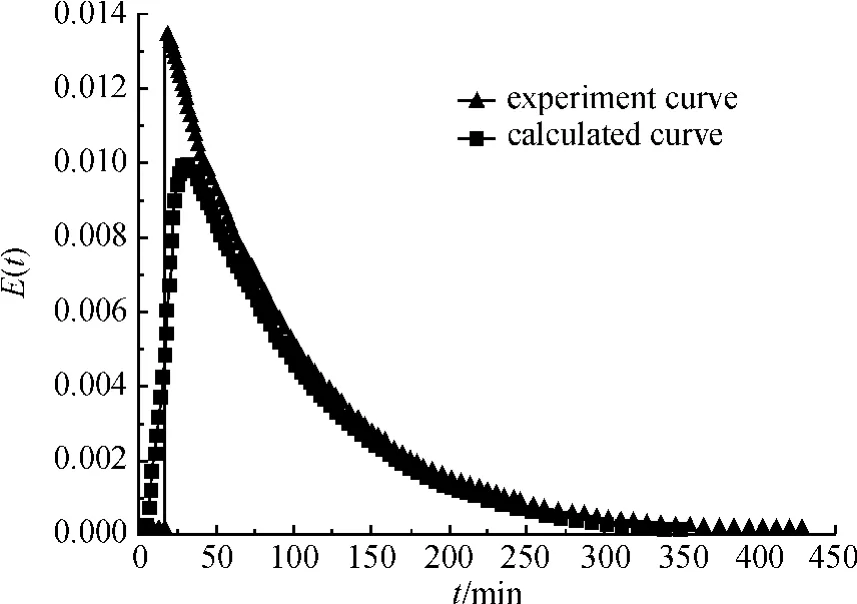
图6 气体流量为38mL／min时E（t）的实验与模型曲线Fig.6 Comparison between experiment curve and model curve when gas flow is 38mL／min

由图6可知：当气体流量为38mL／min时，E（t）最大相对误差为15.0%。

4 结 语

本研究通过对停留时间分布密度函数的求解，建立了厌氧反应器流动模型，模型参数随气体流量的变化而发生一定程度的变化，E（t）方程分别如下：

当气体流量为0mL／min时：

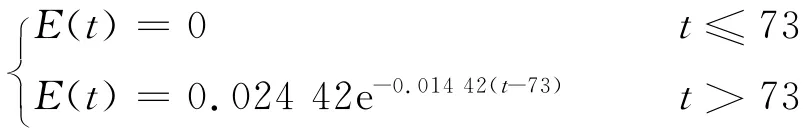
当气体流量为25mL／min时：

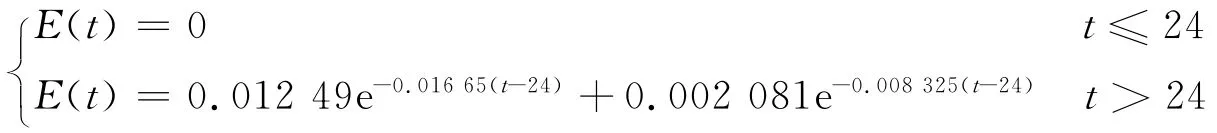
当气体流量为38mL／min时：

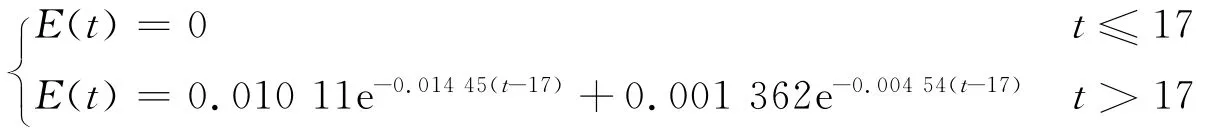
反应器实际运行时，根据实际产生气量大小，对以上三式进行适当内插，便可获得E（t）随时间的变化关系及相应模型参数，进而便可进行反应器的模拟与优化计算了。

［1］ 童昶，沈耀良，赵丹，等.厌氧反应器技术的发展及 ABR反应器的工艺特点［J］.江苏环境科技，2001，14（4）：9-11.

［2］ Tiwarim K，Guha S，Harendranath C S，et al.Influence of extrinsic factors on granulation in UASB reactor［J］.Applied Microbiology and Biotechnology，2006，71（2）：145-154.

［3］ 马三剑，吴建华，刘锋，等.多级内循环（MIC）厌氧反应器的开发应用［J］.中国沼气，2002，20（4）：24-27.

［4］ 冯宗强，袁旭峰，林长松，等，固定床厌氧反应器处理高浓度禽畜粪尿［J］.环境工程学报，2010，4（2）：278-282.

［5］ 楼静.厌氧反应器技术研究开发情况简介［J］.中国环境干部管理学院学报，2002，12（3）：37-40.

［6］ 卢刚，郑平.内循环颗粒污泥床硝化反应器流动模型研究［J］.生物工程学报，2003，19（6）：754-757.

［7］ 张良佺，邵迪.流化床厌氧反应器流化及反应特性研究［J］.环境工程，2011，29（2）：20-23.