计算弯曲变形的几何法

陈合龙，姜凤华，何春木

（台州学院 建筑工程学院，浙江 台州318000）

计算弯曲变形的方法比较多，常用的方法有积分法［1-7］、初参数法［8-10］、能量法［9-12］和虚功法［13］。积分法和初参数法适合计算直杆或折杆弯曲的位移，但无法计算曲杆弯曲的位移；拓展后的积分法可分析超静定结构的弯曲变形问题［6-7］。虚功法基于虚功原理来计算弯曲位移，但是它的计算过程涉及多次弯矩计算，而且每次只能计算一个点在一个方向的位移［13］。实际上，常用方法都回避了弯曲变形问题是几何问题这一本质，因而它们都有缺陷。基于这个思路，本研究从弯曲变形的几何性出发，利用基本的变形-内力关系，笔者找到了计算弯曲变形的新积分法。该方法适用于计算各种形状的杆件的平面弯曲小变形问题，对静定结构和超静定结构弯曲问题的分析步骤也是一致的。因此，该方法不仅是常规方法的重要补充，而且不失为一个计算平面弯曲问题的新选择。

1 公式推导

为了简便起见，以悬臂杆为例。如图1所示，悬臂杆长为l，杆在平面内的抗弯刚度为EI，左端A固定，右端B受集中力F的作用。建立如图所示的坐标系。设杆弯曲的挠曲线方程为w＝w（s），转角方程为θ＝θ（s）。

先计算B端的挠度wB，为此取长度很小的一段杆Δs，查看由于这一小段杆的弯曲造成的B的挠度，如图2所示。

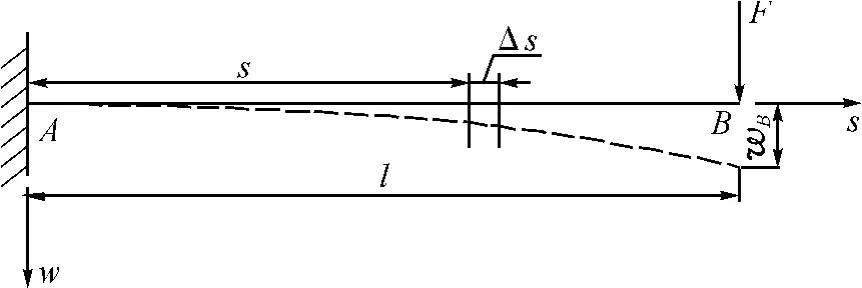
图1 悬臂杆Fig.1 Cantilever bar

图2 微段弯曲Fig.2 Segmented bar under bending

图中，θ（s）为s处的转角，Δθs为微段Δs的转角的改变量。假定杆的变形很小，则：

容易看出，Δw1为s处的转角引起的B端的位移，Δw2＋Δw3为微段Δs的弯曲引起的B端的位移。

在变形很小的情况下，有

将式（5）代入式（3），并利用式（4）：

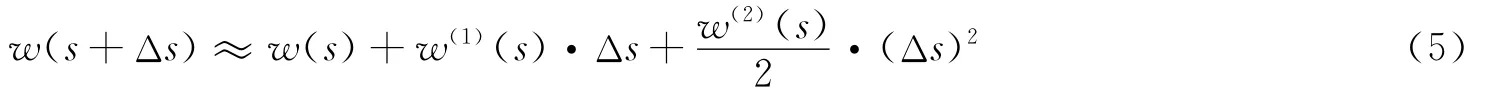
得：

假设s处的曲率半径为ρ，则有

联系式（7），比较式（2）和式（6），可知Δw2相对于Δw3为高阶微量。即：

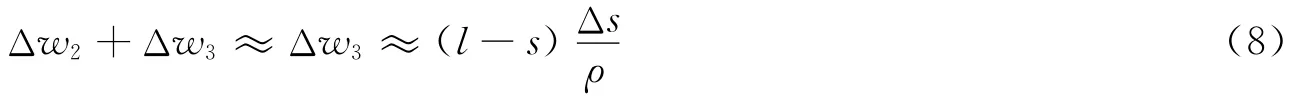
B的挠度wB等于s＝0处的转角引起的B的挠度，对应式（9）等式右边的第一项，加上杆弯曲引起的B的挠度，因此可以这样计算：

2 推广到曲杆

为方便起见，以半径为R的1／4圆弧曲杆为例，如图3所示。杆在平面内的抗弯刚度为EI，A端固定，B端受集中力F作用。建立如图局部坐标系，坐标轴s沿杆的轴向从A到B，τ为在任意s处的切向，并与坐标轴s正向一致。w与坐标轴s处处正交，且从τ绕其起点顺时针旋转90°到达w正向。整体坐标系xoy，原点为A。现在要研究的是在荷载作用下杆的任意位置的位移。设弯曲的挠曲线方程为w＝w（s），转角方程为θ＝θ（s）。

图中τ、w、φ（s）、l（s）都是与s相关的量。其中，l（s）是坐标为s的C点与B的距离，φ（s）为CB在xoy坐标系下的角度。

不难看出，直杆下的计算式（从式（1）到式（13））均可顺利地推广到局部坐标系（ws）下。

同样地，B点的位移可以这样计算：s＝0处的转角引起的B的位移，加上曲杆弯曲引起的B的位移。那么，第一部分由s＝0处的转角引起的B的位移可以表示为：

图3 1／4曲杆Fig.3 1／4curved bar

式（14）和式（15）中，下角标x、y分别表示沿x、y方向的位移，θ（0）为A处的转角，l（0）为AB 的长度，φ（0）为AB与x正向的夹角。

第二部分由曲杆的弯曲引起的B的位移为：

式（16）和式（17）中的下角标s表示对整个曲杆积分的意思。

因此，将式（14）、式（15）、式（16）和式（17）对应相加，即得端点B的位移为：

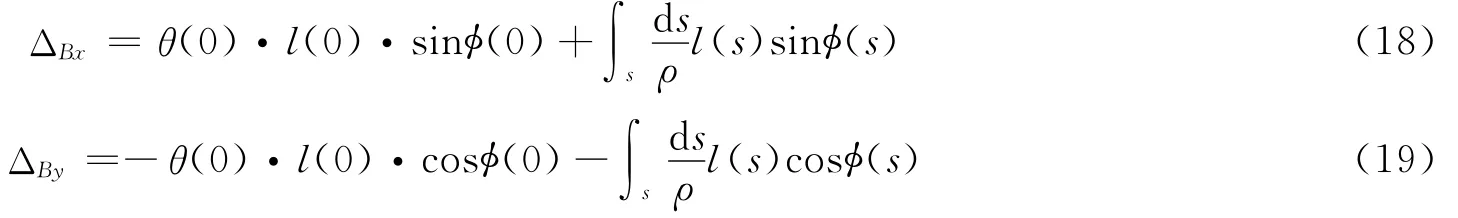
将式（10）代入式（18）、式（19）得，

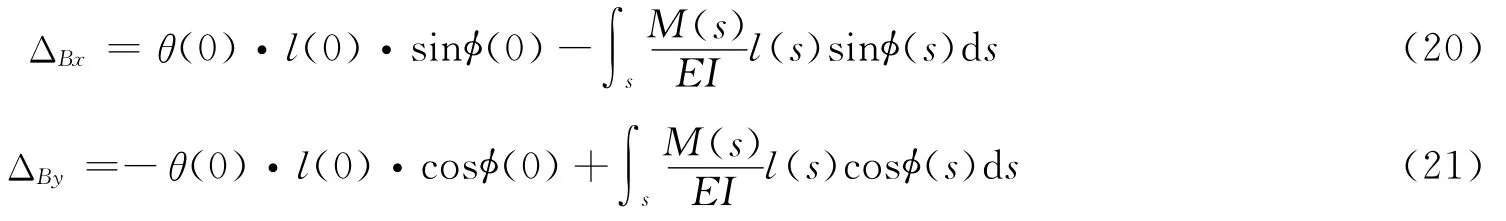
对于任意坐标为s的点的位移的计算式可以表示为：

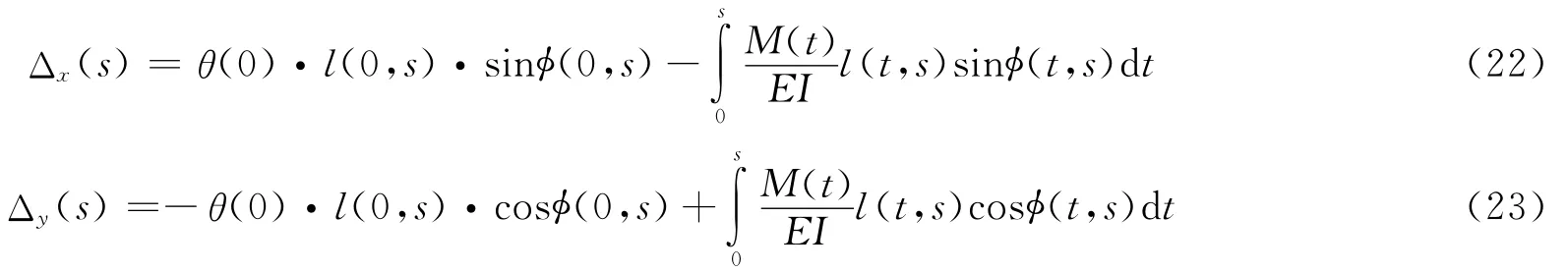
需要说明的是，与式（18）、式（19）中不同，式（22）、式（23）中，l、φ有两个参数，它们是两个点的弧坐标，第一个参数表示第一个点的弧坐标，第二个参数表示第二个点的弧坐标，l表示这两点的距离，φ表示由第一点连向第二点的线段与x轴正向的夹角。

曲杆的转角计算式与直杆的转角计算公式（13）相同。

需要指出的是，对于静定问题，式（12）、式（13）、式（22）和式（23）中只涉及一个初参数（如起点的转角），这个初参数可以是已知的，也可以是待定的；而对于超静定问题，需要增加初参数（起点的转角、弯矩、剪力），以表示出方程中的各项，待定的初参数都可以通过约束条件来确定。

必须说明，弯曲构件的位移主要由弯矩引起，通常不计入轴力和剪力对弯曲位移的影响，以上推导也以此为前提。

3 应用举例

本节将计算图1所示的悬臂杆的挠曲线方程和转角方程，以及图3所示的1／4圆弧杆的位移方程和转角方程。

对于悬臂杆，将弯矩方程M（t）＝-Fl＋Ft及θ（0）＝0代入式（12）中，积分得到悬臂杆的挠曲线方程：

对s求导的转角方程，

式（24）、式（25）的结果与文献［1］一致。

对于1／4圆弧杆，为计算方便，不妨采用极坐标进行计算。如图4所示，对照式（13）、式（22）和式（23），有如下关系式：

将式（26）和弯矩方程 M ＝-FRcosα代入式（13）、式（22）和式（23），得

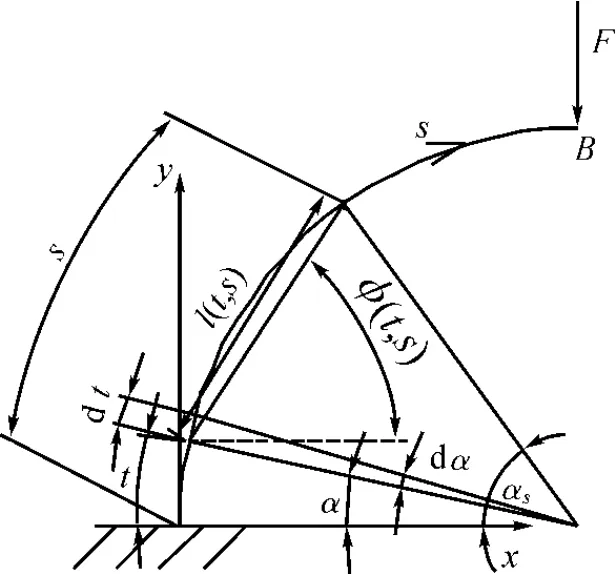
图4 坐标转换Fig.4 Coordinate transformation

积分得，

式（28）的第三方程与文献［13］的结果一致。

对于其他的静定或超静定结构平面弯曲问题的求解，计算步骤是一样的。所不同的是，可能需要利用约束条件来确定起点的待定参数。

4 结 语

本研究从弯曲变形的几何属性出发，推导了计算弯曲变形的新公式，其思路更具一般性，计算也更简便。该方法可以计算曲杆的平面弯曲的变形问题，并且公式中的各项及积分转化成电算也很方便，进一步拓展了它的适用范围。相比于虚功法，其思路更直接，同时避免了虚功法每次计算只能得到一个位移的缺陷。

［1］ 王吉民.材料力学［M］.北京：中国电力出版社，2010.

［2］ 孙训方，方孝淑，关来泰.材料力学I［M］.北京：高等教育出版社，2009.

［3］ 刘鸿文.材料力学Ⅰ［M］.北京：高等教育出版社，2004.

［4］ 单辉祖.材料力学Ⅰ［M］.北京：高等教育出版社，2002.

［5］ 范钦珊，蔡新.材料力学：土木、水利类［M］.北京：清华大学出版社，2009.

［6］ 王秀华，张春秋，门玉涛，等.超静定梁变形计算的积分法［J］.力学与实践，2009，31（4）：79-81.

［7］ 马希龄，张广泰，肖正华.等截面圆弧杆件的转角位移方程［J］.新疆工学院学报，1999，30（2）：79-83.

［8］ 刘庆潭.材料力学教程［M］.北京：机械工业出版社，2006.

［9］ 希伯勒.材料力学［M］.汪越胜，译.北京：电子工业出版社，2006.

［10］ 孙国钧.材料力学［M］.上海：上海交通大学出版社，2006.

［11］ Beer F P，Johnston E R，Sun G J.Mechanics of materials［M］.2ed.New York：McGraw-Hill，1992.

［12］ Gere J M，Timoshenko S P.Mechanics of materials［M］.New York：Von Nostrand Reinhold，1984.

［13］ 朱伯钦，周竞欧，许哲明.结构力学：上册［M］.上海：同济大学出版社，2004：215-216.