二维与三维边坡稳定性分析结果的比较与分析
卢坤林,朱大勇,杨 扬
(合肥工业大学 土木与水利工程学院,合肥 230009)
1 引 言
严格来说,边坡稳定性分析属于空间问题,应采用三维分析方法来研究其稳定性。工程中,常简化为二维平面问题,运用理论成熟的二维分析方法进行稳定性计算,这种处理所带来的误差一直被学者们所关注,如 Baligh等[1]、Gens等[2]、刘华丽等[3]、Eid 等[4]、Farzaneh 等[5]、卢坤林等[6]、陈传胜等[7]、刘红帅等[8]、陈昌富等[9]、Zhang 等[10]均不同程度地开展了这方面的研究。值得指出的是,已有的研究成果比较零散,绝大部分仅讨论了潜在滑体的长高比(L/H)或滑体的空间形状对二维与三维安全系数(分别记为 F2与 F3)计算结果的影响(F3/F2),没有全面系统地讨论各项指标如滑体形态、长高比、坡度、土体参数等对 F3/F2的影响,也未能较好地总结 F3/F2随着各项指标的变化规律,尤其是未能从机制上解释形成上述变化规律的内在原因。
近年来,三维极限平衡法在理论和计算程序上均取得了较大的进展,为进一步研究二维与三维安全系数计算结果间存在的差异及其影响规律提供了理论支撑。本文以均质边坡为研究对象,采用基于滑面正应力修正的极限平衡法及其分析程序[11],详细讨论滑体形态、长高比、坡比、黏聚力、内摩擦角等参数对 F3/F2的影响,总结其内在影响规律,开展了机制分析,为合理正确地评价边坡稳定性提供有价值的理论参考。
2 计算方法与分析模型
2.1 计算方法
朱大勇等研究发现边坡稳定安全系数对潜在滑面上的正应力分布不敏感[12],于是他摒弃传统假定条间力的分析思路,通过假定滑面上的正应力分布,建立满足所有平衡条件的平衡方程,引入恰当的修正函数,求解出安全系数。随后,朱大勇等[13]将这一方法成功地延伸到三维极限平衡中,通过一系列巧妙的数学变换与推演,得到了满足所有6个平衡方程的安全系数显示解答。最近,闫艳等[14]研制了基于滑面正应力修正的二维与三维极限平衡法分析程序,初步实现了二维与三维最危险滑面的搜索及对应的安全系数。本文相关计算成果均在上述计算原理及分析程序的基础上得到的。
2.2 分析模型
所选分析模型为均匀土质边坡,如图1所示,无地下水,根据实际工程常见的边坡失稳模式及尺寸为依据,设定了5个分析指标:滑体形态、滑体长高比、边坡坡比、黏聚力和内摩擦角。依次改变影响指标,分别计算出对应的二维及三维安全系数,在此基础上讨论各指标对 F3/F2的影响规律及其形成机理。

图1 边坡的三维滑面Fig.1 3D slip surface
滑体形态设定5种形式:椭球体、圆柱体、幂函数旋转体、圆柱+两端球体和圆柱+两端圆锥体,滑体长高比(L/H)设定从 1~10变化,边坡坡比 m设定为 0.25、0.50、0.75、1.00、1.25、1.50、1.75、2.00,黏聚力c设定为5、10、15、20、25、30、35、40 kPa,内摩擦角φ设定为 5°、10°、15°、20°、25°、30°、35°和 40°。
3 结果分析
将上述拟定的分析模型及相关参数代入基于滑面正应力修正的极限平衡法分析程序中,依次计算出二维与三维安全系数,并以F3/F2来讨论各指标影响下的二维与三维安全系数的差异及规律。
3.1 滑体形状的影响
图2 为坡比为0.5的土坡(γ=18.8 kN/m3,c=30 kPa,φ= 20°)在不同滑面形式下的F3/F2。由图可见,(1) 除圆柱+两端圆锥体得到的F3/F2偏高,其他几种常见的滑体形式得到的F3/F2基本一致,见图2(a),后续的讨论主要以椭球体为主要滑体形式;(2) 各种滑体形式随着滑体长高比L/H的变化规律一致,F3/F2随着L/H的逐渐增大均呈现先快速减小后逐渐趋缓,见图2(b);(3) 由于三维计算时考虑了端部效应,它对滑体的滑动起到了摩擦抗滑的作用,简化为二维分析模型则忽略了这一有利因素,则有F3/F2≥1,二维安全系数偏于保守;(4) 其他参数情况下结论一致,限于篇幅未给出。

图2 滑体形态与F3/F2的关系曲线Fig.2 Relationships between F3/F2and 3D sliding mass shape
3.2 滑体长高比的影响
已有的研究表明,安全系数与滑体长度关系密切,本文采用了F3/F2与L/H的关系曲线来定性地讨论滑体长度对F3/F2的影响。
图3 为不同坡比下F3/F2与 L/H 的变化关系。由图可见,(1) L/H 对F3/F2的影响比较显著,F3/F2随着 L/H 的增大逐渐减小,并趋于稳定,也就是说,在 L/H 较小时,三维安全系数与二维安全系数差别可高达40%以上,随着滑体长度的不断增大,两者间的误差逐渐减小,最终三维安全系数逼近二维安全系数;(2) F3/F2随 L/H 的变化规律不受坡比、内摩擦角、黏聚力以及滑体形式的影响,但具体数值与上述因素关系密切;(3) 上述变化规律的内在原因是随着滑体长度的不断增大,端部效应在整个抗滑体系中的比重逐渐降低,形成了三维安全系数逐渐趋近二维安全系数的现象。(4) 针对L/H≤ 5.0的滑体,二维稳定性分析误差约为5%~50%,据此得到的稳定性结论过于保守,建议采用三维安全系数来评价边坡的稳定性。

图3 L/H与F3/F2的关系曲线Fig.3 Relationships between F3/F2and L/H
3.3 坡比的影响
图4为坡比m与F3/F2的关系曲线。由图可见,(1) 坡比m对F3/F2的影响也不容忽视,尤其是在黏聚力较大而内摩擦角较小时,误差可高到60%,随着坡比的逐渐增大F3/F2呈减小趋势,两者间的误差逐渐减小;(2) L/H 较小时,F3/F2变化幅度较大,L/H 较大时,F3/F2变化幅度趋缓。以图4(a)为例,当 m 从0.25增至2.00,在L/H=1.0时,F3/F2降幅约为15%,而当L/H=3.0时,降幅仅为5%左右;(3)随着黏聚力的增大和内摩擦角的减小,m对 F3/F2的影响逐渐增强,在图4(a)中,L/H=1时,m从0.25增至 2.00,F3/F2降幅约为 15%,而在图 4(b)和图4(c)中降幅增大至20%和30%左右;(4) 形成上述规律的内在原因在于:m较小时,坡度比较缓,滑体深度较深,随着m的逐渐增大,滑体深度逐渐变浅,端部滑体接触面积也逐渐减小,端部效应也就降低,从而形成了上述变化规律;(5) 在m<1.00时,二维与三维安全系数间的差异约为5%~60%,此时,也建议采用三维安全系数评价边坡稳定性。

图4 坡比与F3/F2的关系曲线Fig.4 Relationships between F3/F2and ratio of slope
3.4 黏聚力的影响
图5 为黏聚力对二维与三维安全系数的影响。由图可见,(1) 在其他指标恒定时,F3/F2随着黏聚力的增大呈递增趋势,如在图5(a)中黏聚力由 5 kPa增至40 kPa,F3/F2由5%~15%增大到10%~35%,也就是说,黏聚力越大,二维与三维安全系数之间的误差也越大;(2) 内摩擦角、长高比以及坡比等指标均不会影响F3/F2与着黏聚力间变化规律,但会影响具体数值;(3) 当其他指标不变时,黏聚力越大,滑面深度越深,端部滑体产生的端部效应增大,出现F3/F2与黏聚力成正相关性的规律;(4) 黏聚力c> 25 kPa时,F3/F2的变化区间约为1.05~1.45,建议开展三维稳定性分析。

图5 黏聚力与F3/F2的关系曲线Fig.5 Relationships between F3/F2and cohesion
3.5 内摩擦角的影响
图6 为内摩擦角对F3/F2影响关系曲线。由图可见,(1) 其他指标不变时,F3/F2随着内摩擦角的增大逐渐减小,即二维与三维安全系数之间的误差随着内摩擦角的逐渐增大而减小;(2) 内摩擦角对F3/F2的影响规律也不受黏聚力、长高比、坡比等指标的影响,但具体数值会受到影响;(3) 当其他指标恒定时,内摩擦角越大,滑面深度越浅,端部滑体产生的端部效应越小,出现F3/F2随着内摩擦角之间增大而减小的规律;(4) 内摩擦角φ < 15°时,二维与三维安全系数间的差异也达到了5%~40%,也需要进行三维稳定性评价。
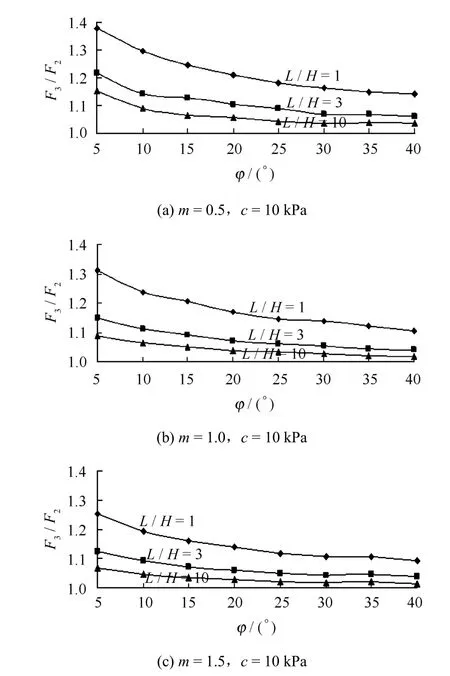
图6 内摩擦角与F3/F2的关系曲线Fig.6 Relationships between F3/F2and internal friction angle
4 讨 论
4.1 二维与三维安全系数及其使用范围建议
边坡失稳破坏属于三维空间问题,三维安全系数更符合实际情况,而二维安全系数是将边坡失稳破坏简化为二维平面问题时得到的,存在一定的近似,因此,三维安全系数较二维安全系数更合理,准确性也更高些。
已有成果和本文的研究均表明,三维安全系数要比二维安全系数高,即二维安全系数是偏保守的,两者间的误差与滑体长高比、滑体形态、坡度、土体参数等指标有关,其中滑体长高比对其影响最为显著。
通过本文研究,笔者建议,(1) 对于滑体长高比L/H≤5的边坡应该采用三维安全系数来评价其稳定性,否则,可能导致过于保守的结论。(2) 对于滑体长高比 5 < L/H ≤ 10且满足下列条件之一的边坡也宜采用三维安全系数来评价其稳定性,即黏聚力c > 25 kPa或内摩擦角φ < 15°或坡比m < 1.00。(3) 对于不在上述范围内的边坡,二维安全系数与三维安全系数之间的误差量在工程允许范围内,可采用二维安全系数来评价边坡的稳定性。类似的建议有:文献[2,3,6,10]认为L/H≤10,文献[7]认为L/H≤4,文献[8]认为L/H≤8时,文献[14]认为L/H≤3~5.5时,应采用三维安全系数来评价边坡的稳定性。
4.2 二维与三维安全系数差异的实质
造成二维与三维安全系数不同的根本原因是滑体的端部效应,二维稳定性分析简化为平面问题,无法考虑滑体端部的抗滑贡献,而三维稳定性分析则能够考虑这一有利因素,造成三维安全系数高于二维安全系数的现象。
对于给定滑体而言,端部抗滑贡献的大小不随着滑体长度的变化而改变,因此,随着滑体长度的增大,端部抗滑效应在整个抗滑体系中的相对密度逐渐降低,形成随着滑体长度的增加,三维安全系数逐渐趋近二维安全系数的现象。
其他指标不变时,最危险滑面的位置随着黏聚力的增大逐渐变深,滑体端部接触面积也逐渐增大,进而端部抗滑效应也增大,三维与二维安全系数之间的差别也随之增大,形成F3/F2与黏聚力呈正相关的规律。同理,内摩擦角及坡比的减小也会造成最危险滑面位置变深,增大了端部效应,形成了F3/F2随着内摩擦角及坡比的减小逐渐递增的规律。
5 结 论
(1) F3/F2与滑体长高比、滑体形态、坡度、土体参数等指标有关,F3/F2随着长高比、内摩擦角及坡比的增大逐渐减小,随着黏聚力的增大逐渐增大,其中滑体长高比对其影响最为显著。
(2) 造成二维与三维安全系数差异的本质在于滑体的端部效应,各影响因素的变化引起了端部抗滑效应在整个抗滑体系中的相对密度的发生改变,从而形成上述规律。
鉴于三维稳定性分析得复杂性,目前尚不能为工程技术人员充分掌握,二维稳定性分析仍为主流分析手段,根据本文研究成果,从工程应用的角度建议了需要考虑三维稳定性分析的标准,为合理开展边坡稳定性分析提供理论支持。
[1]BALIGH M M,AZZOUZ A S. End effects on cohesive slopes[J]. Journal of Geotechnical Engineering,ASCE,1975,101(11): 1105-1107.
[2]GENS A,HUTCHISION J N,CAVOUNIDIS S. Threedimensional analysis of slides in cohesive soils[J].Geotechnique,1988,38(1): 1-23.
[3]刘华丽. 基于滑面正应力分布的边坡二维与三维稳定性计算方法[博士学位论文 D]. 南京: 中国人民解放军理工大学,2006.
[4]EID H T,ELLEBOUDY A M,ELMARSAFAWI H G.Stability analysis and charts for slopes susceptible to translational failure[J]. Canadian Geotechnical Journal,2006,43(12): 1374-1388.
[5]FARZANEH O,ASKARI F,GANJIAN N. Threedimensional stability analysis of convex slopes in plan view[J]. Journal of Geotechnical and Geoenvironmental Engineering,2008,134 (8): 1192-1200.
[6]卢坤林,朱大勇,许强. 三维滑裂面形状对安全系数的影响[J]. 岩石力学与工程学报,2009,28(增刊2): 3679-3685.LU Kun-lin,ZHU Da-yong,XU Qiang. Impact of 3D slip surface’s shape on factor of safety[J]. Chinese Journal of Rock Mechanics and Engineering,2009,28(Supp.2):3679-3685.
[7]陈传胜,蒋欣. 三维与二维滑坡稳定分析的比较研究[J]. 自然灾害学报,2009,18(1): 194-198.CHEN Chuan-sheng,JIANG Xin. Comparative study of 3D and 2D landslide stability analyses[J]. Journal of Natural Disasters,2009,18(1): 194-198.
[8]刘红帅,年廷凯,万少石. 三维边坡稳定性分析中的边界约束效应[J]. 吉林大学学报(地球科学版),2010,40(3): 638-644.LIU Hong-shuai,NIAN Ting-kai,WAN Shao-shi. Effect of boundary constraint condition on the stability analysis of 3D slope[J]. Journal of Jilin University (Earth Science Edition),2010,40(3): 638-644.
[9]陈昌富,朱剑锋. 基于 Morgenstern-Price 法边坡三维稳定性分析[J]. 岩石力学与工程学报,2010,29(7):1473-1480.CHEN Chang-fu,ZHU Jian-feng. A three-dimensional slope stability analysis procedure based on Morgenstern-Price method[J]. Chinese Journal of Rock Mechanics and Engineering,2010,29(7): 1473-1480.
[10]ZHANG Ke,CAO Ping,LIU Zi-yao,et al. Simulation analysis on three-dimensional slope failure under different conditions[J]. Transactions of Nonferrous Metals Society of China (English Edition),2011,21(11): 2490-2502.
[11]ZHU D Y,LEE C F. Explicit limit equilibrium solution for slope stability[J]. International Journal for Numerical and Analytical Methods in Geomechanics,2002,26(15): 1573-1590.
[12]朱大勇,李焯芬,姜弘道,等. 基于滑面正应力修正的边坡安全系数解答[J]. 岩石力学与工程学报,2004,23(16): 2788-2791.ZHU Da-yong,LEE C F,JIANG Hong-dao,et al.Solution of slope safety factor by modifying normal stresses over slip suface[J]. Chinese Journal of Rock Mechanics and Engineering,2004,23(16): 2788-2791.
[13]朱大勇,钱七虎. 三维边坡严格与准严格极限平衡解答及工程应用[J]. 岩石力学与工程学报,2007,26(8):1513-1528.ZHU Da-yong,QIAN Qi-hu. Rigors and quasi-rigors limit equilibrium solutions of 3D slope stability and application to engineering[J]. Chinese Journal of Rock Mechanics and Engineering,2007,26(8): 1513-1528.
[14]闫艳,朱大勇. 对称边坡三维临界滑动面的确定[J]. 合肥工业大学学报(自然科学版),2011,34(11): 1682-1686.YAN Yan,ZHU Da-yong. Determination of threedimensional critical slip surface of a symmetrical slope[J].Journal of Hefei University of Technology (Natural Science),2011,34(11): 1682-1686.

